[PYTHON] [Übersetzung] scikit-learn 0.18 Benutzerhandbuch 2.8. Dichteschätzung

google übersetzte http://scikit-learn.org/0.18/modules/density.html [scikit-learn 0.18 Benutzerhandbuch 2. Lernen ohne Lehrer](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA Von% E3% 81% 97% E5% AD% A6% E7% BF% 92)

2.8. Dichteschätzung

Die Dichteschätzung folgt der Grenze zwischen unbeaufsichtigtem Lernen, Feature-Engineering und Datenmodellierung. Einige der gebräuchlichsten und nützlichsten Dichteschätztechniken sind Gaußsche Gemische (sklearn.mixture.GaussianMixture. .mixture.GaussianMixture)) und Schätzung der Kerneldichte (sklearn.neighbors.KernelDensity .neighbors.KernelDensity)) ist ein nachbarschaftsbasierter Ansatz. Das Gaußsche Mischen wird im Zusammenhang mit Clustering (http://scikit-learn.org/0.18/modules/clustering.html#clustering) ausführlicher beschrieben. Dies dient auch als unbeaufsichtigtes Clustering-Schema. Die Dichteschätzung ist ein sehr einfaches Konzept, und die meisten Menschen sind bereits mit der beliebten Dichteschätzmethode Histogramm vertraut.

2.8.1. Dichteschätzung: Histogramm

Ein Histogramm ist eine einfache Visualisierung der Daten, in denen Bins definiert sind, und fasst die Anzahl der Datenpunkte in jedem Bin zusammen. Ein Beispiel für das Histogramm wird im oberen linken Bereich der folgenden Abbildung angezeigt.

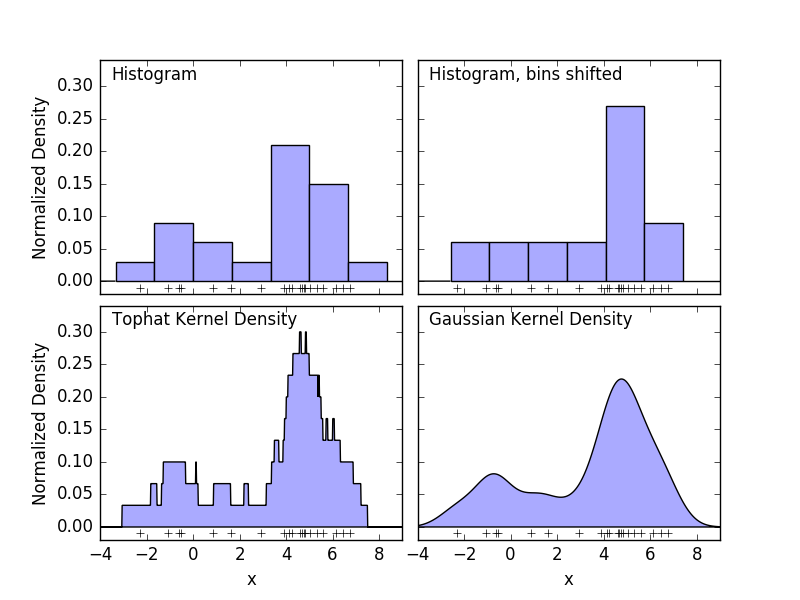
Das große Problem bei Histogrammen besteht jedoch darin, dass die Auswahl von Binning einen unverhältnismäßigen Einfluss auf die resultierende Visualisierung haben kann. Betrachten Sie das obere rechte Feld in der Abbildung oben. Verschieben Sie den Behälter nach rechts, um ein Histogramm derselben Daten anzuzeigen. Die Ergebnisse der beiden Visualisierungen können sehr unterschiedlich aussehen und die Interpretation der Daten kann unterschiedlich sein. Intuitiv können Sie sich das Histogramm als einen Stapel von Blöcken vorstellen, einen Block pro Punkt. Stellen Sie das Histogramm wieder her, indem Sie Blöcke im entsprechenden Rasterraum stapeln. Was aber, wenn Sie anstelle des Stapelns von Blöcken in einem regulären Raster jeden Block in die Mitte des Punktes stellen, den er darstellt, und die Gesamthöhe jeder Position summieren? Diese Idee führt zur Visualisierung unten links. Vielleicht nicht so sauber wie ein Histogramm, aber die Tatsache, dass die Daten die Position des Blocks bestimmen, bedeutet, dass die zugrunde liegenden Daten viel besser dargestellt werden. Diese Visualisierung ist ein Beispiel für die Schätzung der Kerneldichte. In diesem Fall verwenden wir den Zylinderkernel (quadratische Blöcke an jedem Punkt). Sie können eine flüssigere Verteilung wiederherstellen, indem Sie einen reibungsloseren Kernel verwenden. Das Diagramm unten rechts zeigt die Schätzung der Gaußschen Kerndichte. Hier gibt jeder Punkt der Summe eine Gaußsche Kurve. Das Ergebnis ist eine aus den Daten abgeleitete Schätzung der glatten Dichte, die als leistungsfähiges nichtparametrisches Modell der Punktverteilung fungiert.

2.8.2 Kernel-Dichteschätzung

Die Schätzung der Kerneldichte in scikit-learn lautet sklearn.neighbors.KernelDensity Es ist implementiert. Für effiziente Abfragen wird ein Ball- oder KD-Baum verwendet (siehe Nächste Nachbarn für diese Diskussionen). bitte beziehen Sie sich auf). Das obige Beispiel verwendet der Einfachheit halber einen 1D-Datensatz, aber die Schätzung der Kerneldichte kann in einer beliebigen Anzahl von Dimensionen durchgeführt werden. In der Realität verringert der Fluch der Dimension jedoch die Leistung auf einem höheren Niveau.

Die folgende Abbildung zeigt 100 Punkte aus der bimodalen Verteilung und liefert Schätzungen der Kerneldichte für die drei Kerneloptionen.

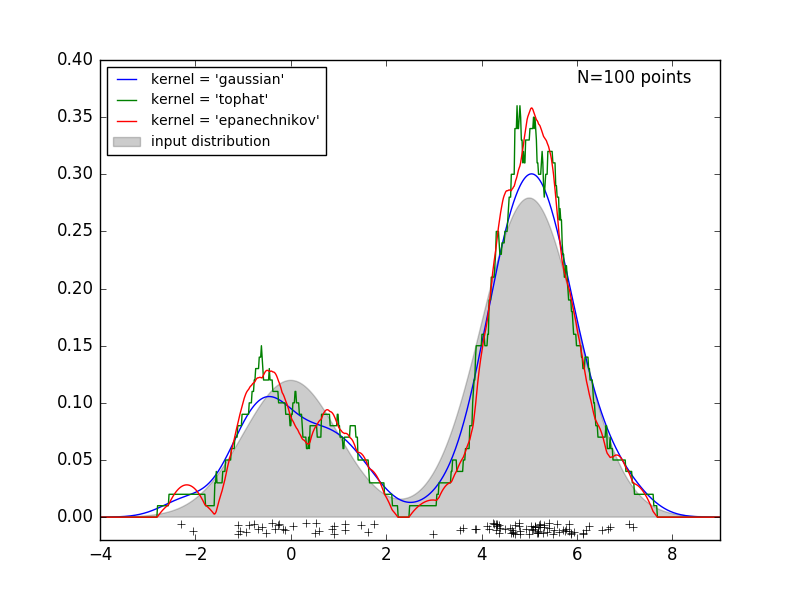
Es ist klar, wie sich die Kernelform auf die Glätte der resultierenden Verteilung auswirkt. Der Scikit-Learn-Kernel-Dichteschätzer kann wie folgt verwendet werden:

>>> from sklearn.neighbors.kde import KernelDensity
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
>>> kde.score_samples(X)
array([-0.41075698, -0.41075698, -0.41076071, -0.41075698, -0.41075698,
       -0.41076071])

Hier verwenden wir "kernel =" gaussian "wie oben. Mathematisch ist der Kernel eine positive Funktion $ K (x; h) $, die durch den Bandbreitenparameter $ h $ gesteuert wird. In Anbetracht dieser Kernelform ist die Dichteschätzung am Punkt y in der Punktgruppe N gegeben durch:

\rho_K(y) = \sum_{i=1}^{N} K((y - x_i) / h)

Die Bandbreite wirkt hier als Glättungsparameter und steuert den Kompromiss zwischen Vorspannung und Streuung in den Ergebnissen. Eine große Bandbreite führt zu einer sehr gleichmäßigen (dh stark vorgespannten) Dichteverteilung. Eine schmale Bandbreite führt zu einer nicht glatten (dh stark dispergierten) Dichteverteilung. sklearn.neighbors.KernelDensity implementiert einige beliebte Kernelformate. Dies ist in der folgenden Abbildung dargestellt.

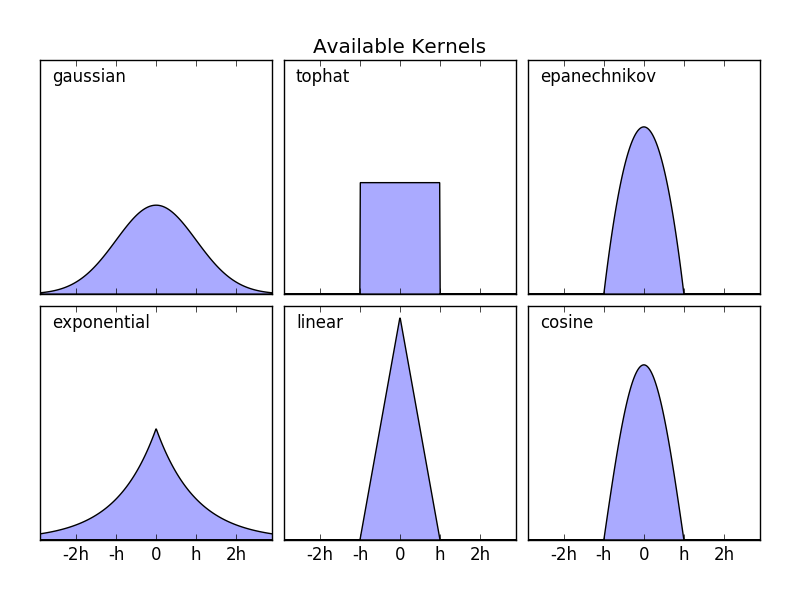
Das Format dieser Kernel ist:

• Gaußscher Kernel "Kernel =" Gaußscher "
  • K(x; h) \propto \exp(- \frac{x^2}{2h^2} )
• Tophat-Kernel kernel = 'tophat'
  • K(x; h) \propto 1 if x < h
• Epanechnikov-Kernel kernel = 'epanechnikov'
  • K(x; h) \propto 1 - \frac{x^2}{h^2}
• Exponentieller Kernel kernel = 'exponentiell'
  • K(x; h) \propto \exp(-x/h)
• Linearer Kernel kernel = 'linear'
  • K(x; h) \propto 1 - x/h if x < h
• Cosinus-Kernel Kernel = 'Cosinus'
  • K(x; h) \propto \cos(\frac{\pi x}{2h}) if x < h

Die Kerneldichteschätzung ist eine gültige Entfernungsmetrik (sklearn.neighbors.DistanceMetric Sie können jede dieser Methoden verwenden (siehe), aber die Ergebnisse werden nur für euklidische Metriken ordnungsgemäß normalisiert. Eine besonders nützliche Metrik ist der Haversine-Abstand (https://en.wikipedia.org/wiki/Haversine_formula), der den Winkelabstand zwischen Punkten auf einer Kugel misst. Im folgenden Beispiel wird die Kerneldichteschätzung zur Visualisierung von Geodaten verwendet. In diesem Beispiel die Verteilung der Beobachtungen für zwei verschiedene Arten auf dem südamerikanischen Kontinent:

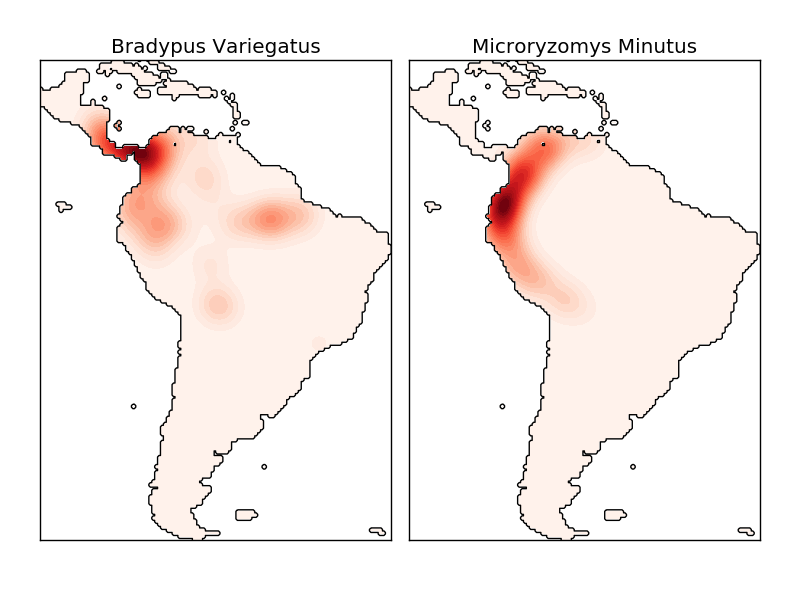
Eine weitere nützliche Anwendung der Kernel-Dichteschätzung besteht darin, ein nicht parametrisches Generierungsmodell eines Datensatzes zu trainieren, um aus diesem Generierungsmodell effizient neue Stichproben abzuleiten. Hier ist ein Beispiel für die Verwendung dieses Prozesses zum Erstellen eines neuen Satzes handgeschriebener Zahlen unter Verwendung des in der PCA-Projektion von Daten erlernten Gaußschen Kernels.

Die "neuen" Daten bestehen aus einer linearen Kombination von Eingabedaten und werden wahrscheinlich unter der Annahme eines KDE-Modells gezeichnet.

• Beispiel:
• Einfache Schätzung der 1D-Kerneldichte: 1 Berechnung einfacher Kernel-Dichteschätzungen in Dimensionen.
• Schätzung der Kerneldichte: Kartendichte Ein Beispiel für die Verwendung der Schätzung zum Trainieren eines Modells zum Generieren handgeschriebener numerischer Daten und zum Zeichnen einer neuen Stichprobe aus diesem Modell.
• Schätzung der Kernel-Dichte der Artenverteilung: Geografie Ein Beispiel für die Schätzung der Kerneldichte unter Verwendung der Haversine-Abstandsmetrik zur Visualisierung von Geodaten

[scikit-learn 0.18 Benutzerhandbuch 2. Lernen ohne Lehrer](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA Von% E3% 81% 97% E5% AD% A6% E7% BF% 92)

© 2010 - 2016, Entwickler von Scikit-Learn (BSD-Lizenz).