[PYTHON] [Übersetzung] scikit-learn 0.18 Benutzerhandbuch 1.16. Wahrscheinlichkeitskalibrierung

google übersetzte http://scikit-learn.org/0.18/modules/calibration.html [scikit-learn 0.18 Benutzerhandbuch 1. Überwachtes Lernen](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98 Von% E3% 81% 8D% E5% AD% A6% E7% BF% 92)

1.16 Wahrscheinlichkeitskalibrierung

Bei der Durchführung von Klassifizierungen sagen wir häufig nicht nur Klassenbezeichnungen voraus, sondern ermitteln auch die Wahrscheinlichkeit für jede Bezeichnung. Diese Wahrscheinlichkeit gibt ein gewisses Vertrauen in die Vorhersage. Einige Modelle haben schlechte Schätzungen der Klassenwahrscheinlichkeiten, während andere keine probabilistische Vorhersage unterstützen. Mit Kalibrierungsmodulen können Sie die Wahrscheinlichkeiten eines bestimmten Modells besser anpassen oder die Wahrscheinlichkeitsvorhersage unterstützen. Ein gut kalibrierter Klassifikator ist ein probabilistischer Klassifikator, der die Ausgabe der Predict_proba-Methode direkt als Konfidenzniveau interpretieren kann. Zum Beispiel gehören ungefähr 80% der Proben, denen von einem gut kalibrierten (binären) Klassifikator ein Predict_proba-Wert von 0,8 gegeben wurde, tatsächlich zur positiven Klasse. Das folgende Diagramm vergleicht, wie gut die Wahrscheinlichkeitsvorhersagen der verschiedenen Klassifikatoren kalibriert sind.

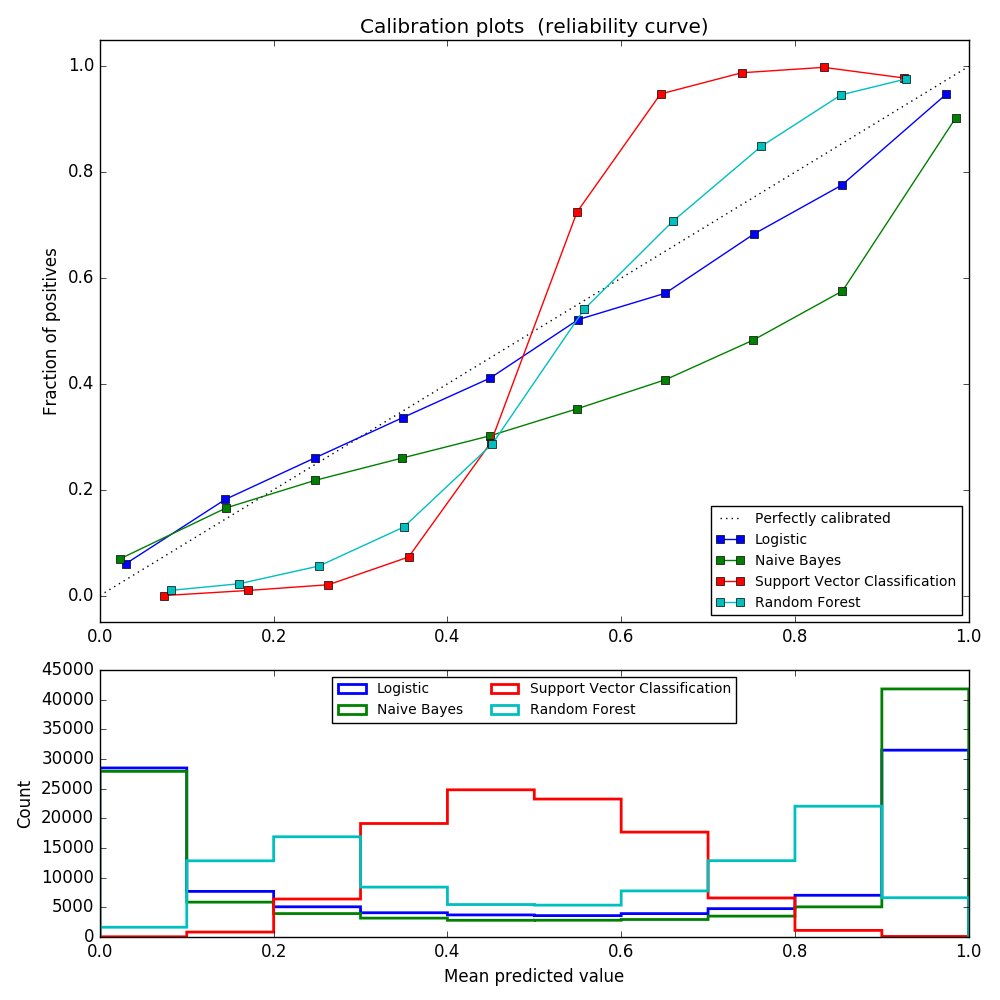
LogisticRegression () gibt standardmäßig eine ordnungsgemäß kalibrierte Vorhersage zur direkten Optimierung des Protokollverlusts zurück. Im Gegensatz dazu geben andere Methoden eine voreingenommene Wahrscheinlichkeit zurück. Jede Methode hat eine andere Tendenz:

• GaussianNB tendiert dazu, die Wahrscheinlichkeit auf 0 oder 1 zu verschieben (beachten Sie die Anzahl der Histogramme). Dies liegt an der Annahme, dass die Merkmale bei Angabe der Klasse bedingt unabhängig sind. Dies ist bei diesem Datensatz mit zwei redundanten Funktionen nicht der Fall.
• RandomForestClassifier zeigt das entgegengesetzte Verhalten. Das Histogramm zeigt Peaks mit einer Wahrscheinlichkeit von etwa 0,2 und 0,9, und die Wahrscheinlichkeit, nahe bei 0 oder 1 zu sein, ist sehr selten. Dies wird von Niculescu-Mizil und Caruana [4] erklärt. "Methoden zur Mittelung von Vorhersagen aus dem Basissatz von Modellen, wie z. B. Absacken und zufällige Wälder, beeinflussen die Vorhersagen, dass sich die zugrunde liegende Varianz des Basismodells aus diesen Werten 0 oder 1 annähern sollte, also auf 0 und 1 gesetzt. Dies macht enge Vorhersagen schwierig. Da Vorhersagen auf das Intervall [0,1] beschränkt sind, liegt der Fehler aufgrund der Varianz tendenziell auf einer Seite nahe 0 und 1. Das Modell ist beispielsweise für einen Fall. Wenn Sie p = 0 vorhersagen müssen, können Sie dies nur durch Absacken erreichen, indem alle Buggy-Bäume Null vorhersagen. Dieses Rauschen erzeugt einen Baum, der in diesem Fall Werte größer als 0 vorhersagt, wodurch sich die durchschnittliche Vorhersage des Hintergrundeensembles von 0 wegbewegt. Bäume auf Basisebene, die in zufälligen Wäldern trainiert werden, sind Teilmengen von Merkmalen. Dieser Effekt wird in zufälligen Wäldern aufgrund seiner relativ großen Streuung am stärksten beobachtet. " Infolgedessen zeigt die Kalibrierungskurve eine charakteristische Sigmoidform, was darauf hinweist, dass sich der Klassifizierer mehr auf seine "Intuition" verlassen und im Allgemeinen eine Wahrscheinlichkeit nahe 0 oder 1 zurückgeben kann.
• Die Klassifizierung des linearen Unterstützungsvektors (LinearSVC) weist eine größere Sigmoidkurve als RandomForestClassifier auf. zeigen. Dies ist bei der Maximum-Margin-Methode (im Vergleich zu Niculescu-Mizil und Caruana [4]) üblich, bei der harte Proben nahe der Entscheidungsgrenze im Mittelpunkt stehen.

Zwei Ansätze zur Durchführung einer probabilistischen Vorhersagekalibrierung: ein parametrischer Ansatz basierend auf dem Pratt-Sigmoidmodell und einer isotonischen Regression (sklearn.isotonic) ) Wird als nicht parametrischer Ansatz bereitgestellt. Sie müssen eine probabilistische Kalibrierung für neue Daten durchführen, die nicht für die Modellanpassung verwendet werden. CalibratedClassifierCV Die Klasse ist ein Modell für das Trainingsmuster unter Verwendung des Kreuzvalidierungsgenerators. Schätzen Sie jede Aufteilung der Parameter und Kalibrierung der Testprobe. Dann werden die erwarteten Wahrscheinlichkeiten für die Falte gemittelt. Bereits angepasste Klassifikatoren können von CalibratedClassifierCV über den Parameter cv =" prefit " kalibriert werden. In diesem Fall muss der Benutzer manuell feststellen, dass die Daten zum Anpassen und Kalibrieren des Modells diskontinuierlich sind.

Das folgende Bild zeigt die Vorteile der stochastischen Kalibrierung. Das erste Bild zeigt zwei Klassen und drei Teile des Datensatzes. Der zentrale Block enthält eine Zufallsstichprobe jeder Klasse. Die Wahrscheinlichkeit einer Probe dieser Masse sollte 0,5 betragen.

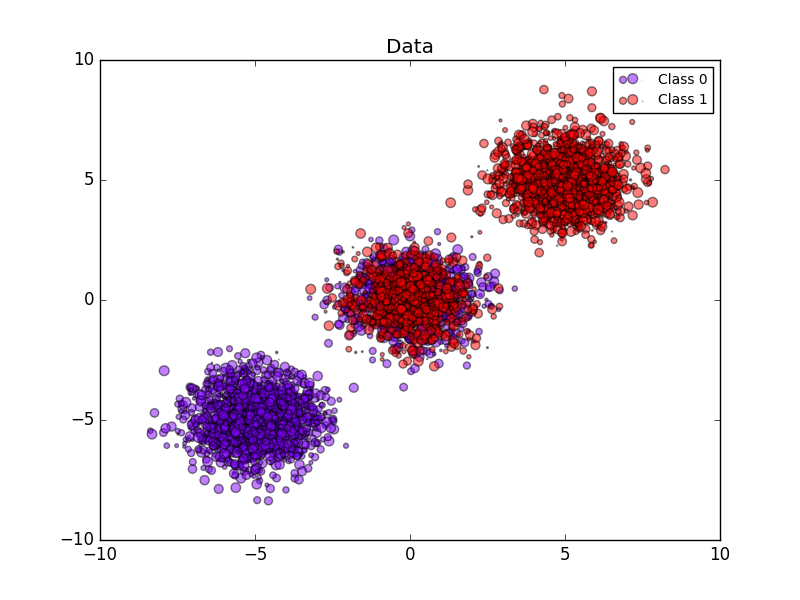
Das folgende Bild zeigt Daten über der geschätzten Wahrscheinlichkeit unter Verwendung des nicht kalibrierten Gaußschen naiven Bayes-Klassifikators, der Sigmoidkalibrierung und der nichtparametrischen isotonischen Kalibrierung. Es kann beobachtet werden, dass das nichtparametrische Modell die genaueste Wahrscheinlichkeitsschätzung für die zentrale Stichprobe liefert, 0,5.

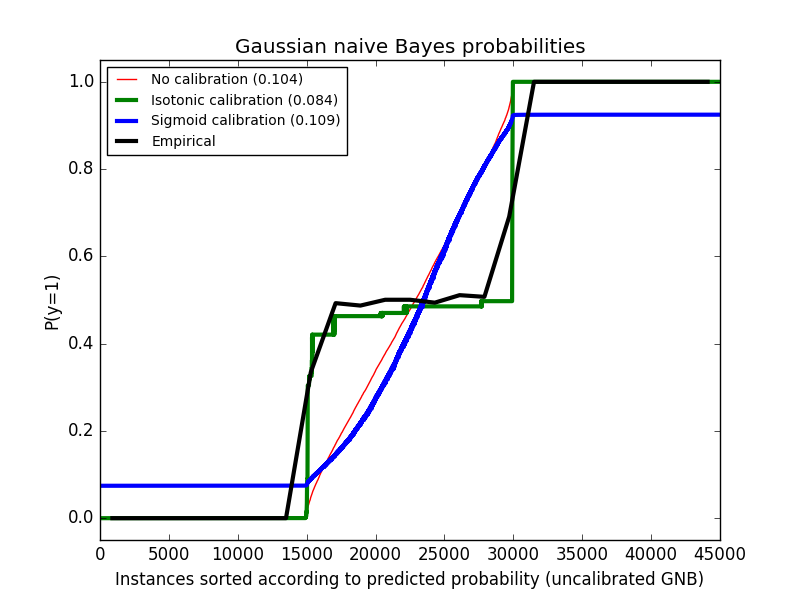
Das folgende Experiment wird an einem künstlichen Datensatz zur binären Klassifizierung mit 100.000 Stichproben mit 20 Merkmalen durchgeführt (1.000 Stichproben werden für die Modellanpassung verwendet). Von den 20 Funktionen sind nur 2 nützlich und 10 redundant. Diese Abbildung zeigt die geschätzten Wahrscheinlichkeiten, die mit einem linearen SVC sowohl mit logistischer Regression als auch mit einem linearen Unterstützungsvektorklassifikator (SVC) sowie isotonischen und sigmoidalen Kalibrierungen erhalten wurden. Die Kalibrierungsleistung wird anhand des Brier-Scores brier_score_loss bewertet und in der Legende ( Kleiner ist besser).

Hier können wir sehen, dass die logistische Regression kalibriert ist, weil ihre Kurven nahezu diagonal sind. Die lineare SVC-Kalibrierungslinie weist eine Sigmoidkurve auf, die nur für "sichere" Klassifikatoren gilt. Bei LinearSVC wird dies durch die Randeigenschaft des Scharnierverlusts verursacht. Dadurch kann sich das Modell auf harte Proben (Unterstützungsvektoren) nahe der Entscheidungsgrenze konzentrieren. Beide Kalibrierungsarten lösen dieses Problem und liefern fast die gleichen Ergebnisse. Die folgende Abbildung zeigt eine Gaußsche Naive-Bayes-Kalibrierungskurve mit denselben Daten mit und ohne beide Kalibrierungsarten.

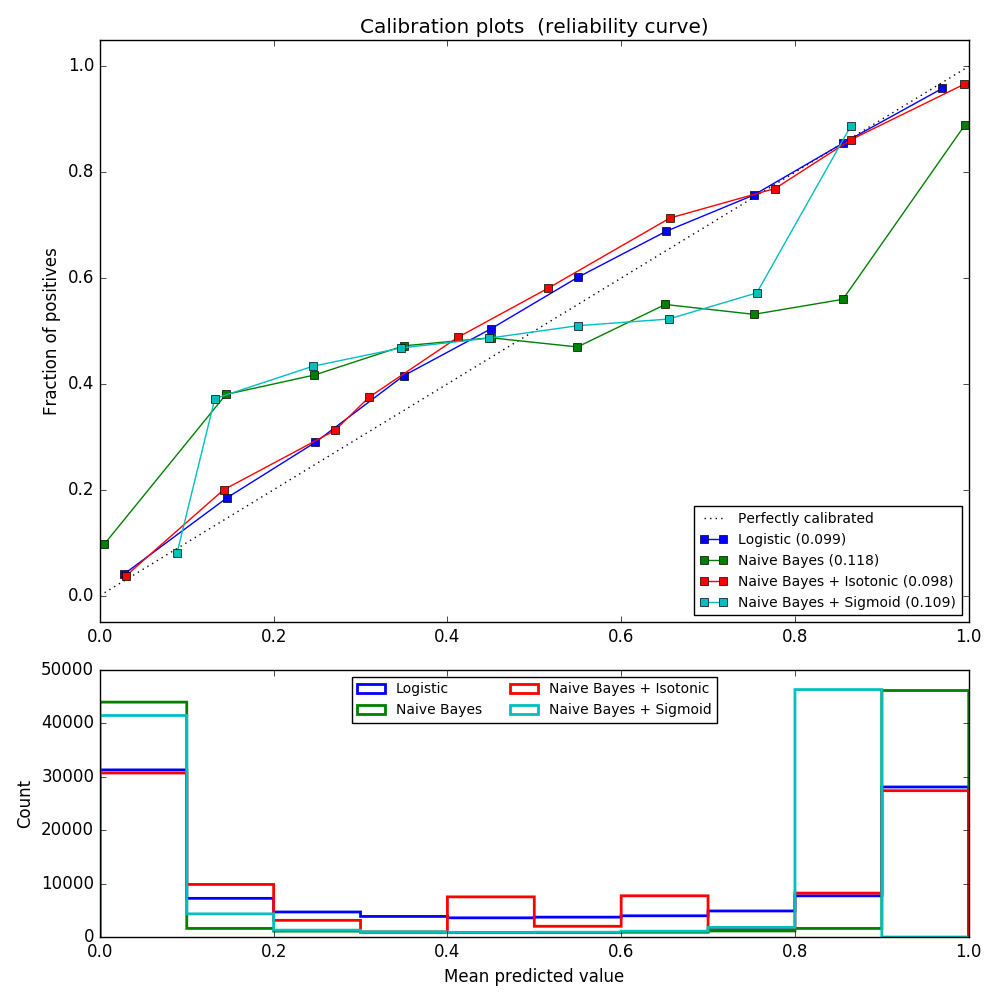
Gaußsche naive Bayes liefern sehr schlechte Ergebnisse, aber es stellt sich heraus, dass dies auf andere Weise als durch lineare SVC erfolgt. Die lineare SVC zeigt eine Sigmoid-Kalibrierungskurve, während die Gaußsche naive Bayes-Kalibrierungskurve eine transponierte Sigmoidform aufweist. Dies ist häufig bei zu optimistischen Klassifikatoren der Fall. In diesem Fall wird das Überbewusstsein des Klassifikators durch redundante Merkmale verursacht, die gegen die merkmalsunabhängige Annahme von Naive Bayes verstoßen. Die isotonische Regressionswahrscheinlichkeitskalibrierung nach Gaußscher naiver Bayes kann dieses Problem beheben, wie aus den nahezu diagonalen Kalibrierungskurven hervorgeht. Die Sigmaid-Kalibrierung ist auch nicht so leistungsfähig wie die nichtparametrische isotonische Kalibrierung, verbessert jedoch den Brier-Score geringfügig. Dies ist eine wesentliche Einschränkung der Sigmoidkalibrierung, und ihre parametrische Form nimmt eher Sigmoide als transponierte Sigmoidkurven an. Das nichtparametrische isotonische Kalibrierungsmodell macht jedoch keine so starken Annahmen und kann jede Form mit ausreichenden Kalibrierungsdaten verarbeiten. Im Allgemeinen wird die Sigmoidkalibrierung bevorzugt, wenn die Kalibrierungskurve sigmoid ist und die Kalibrierungsdaten begrenzt sind. Die isotonische Kalibrierung wird jedoch in Situationen bevorzugt, in denen eine große Datenmenge für Nicht-Sigmoidkalibrierungskurven und -kalibrierungen verfügbar ist. CalibratedClassifierCV ist mehr als eins, wenn die Basisschätzung dies kann. Es kann auch Klassifizierungsaufgaben ausführen, die Klassen enthalten. In diesem Fall wird der Klassifikator für jede Klasse einzeln auf unterschiedliche Weise eins zu eins kalibriert. Bei der Vorhersage der Wahrscheinlichkeit unsichtbarer Daten wird die kalibrierte Wahrscheinlichkeit jeder Klasse separat vorhergesagt. Da ihre Wahrscheinlichkeiten nicht immer mit 1 übereinstimmen, werden sie nachbearbeitet, um sie zu normalisieren. Das folgende Bild zeigt, wie die Sigmoidkalibrierung die Vorhersagewahrscheinlichkeit eines Klassifizierungsproblems mit drei Klassen ändert. Ein Beispiel ist ein Standard-2-Simplex mit 3 Ecken, die 3 Klassen entsprechen. Der Pfeil zeigt vom vom nicht kalibrierten Klassifizierer vorhergesagten Wahrscheinlichkeitsvektor zum vom gleichen Klassifizierer nach der Sigmoidkalibrierung des Holdout-Validierungssatzes vorhergesagten Wahrscheinlichkeitsvektor. Die Farbe gibt die wahre Klasse der Instanz an (rot: Klasse 1, grün: Klasse 2, blau: Klasse 3).

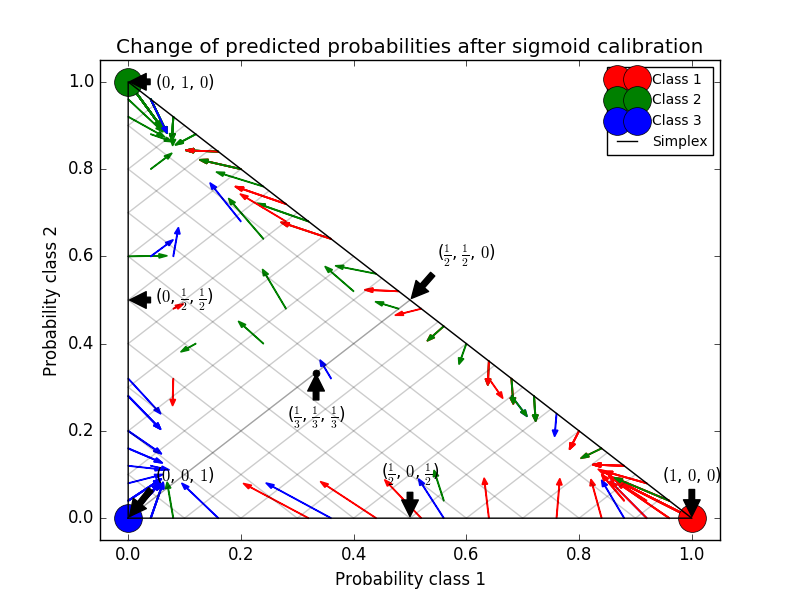
Der Basisklassifizierer ist ein zufälliger Waldklassifizierer mit 25 Basisschätzern (Bäumen). Wenn dieser Klassifikator an allen 800 Trainingsdatenpunkten trainiert wird, sind die Vorhersagen zu sicher und führen zu erheblichen Protokollverlusten. Bei den verbleibenden 200 Datenpunkten verringert die Kalibrierung desselben an 600 Datenpunkten trainierten Klassifikators mit "method =" sigmoid "die Zuverlässigkeit der Vorhersage, dh der Kante des Simplex. Verschieben Sie den Wahrscheinlichkeitsvektor von in die Mitte.

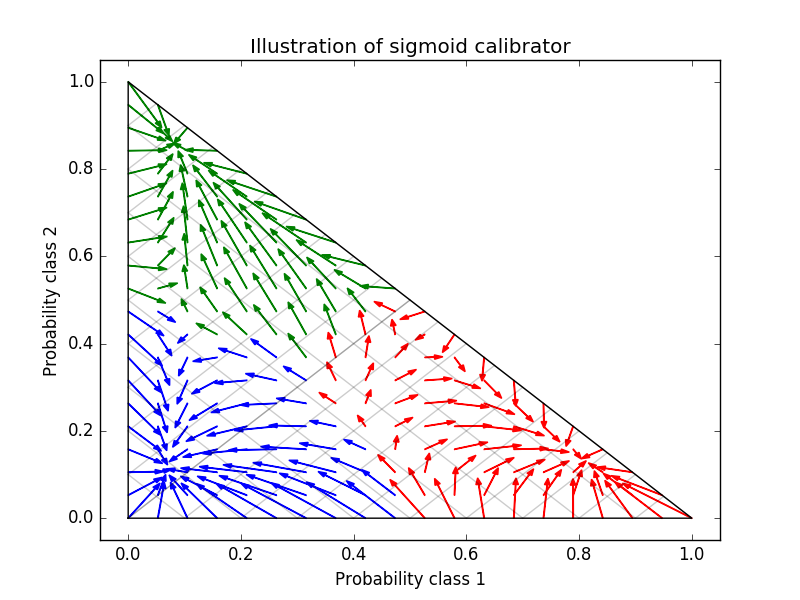
Diese Kalibrierung führt zu einem geringeren Protokollverlust. Beachten Sie, dass die Alternative darin bestand, die Anzahl der Basisschätzungen zu erhöhen, die zu einer ähnlichen Verringerung des logarithmischen Verlusts führen würden.

• Verweise:
• [1] Erhalten Sie kalibrierte probabilistische Schätzungen von Entscheidungsbäumen und naiven Bayes-Klassifikatoren, B. Zadrozny & C. Elkan, ICML 2001
• [2] Konvertieren Sie Klassifikator-Scores in genaue Wahrscheinlichkeitsschätzungen für mehrere Klassen, B. Zadrozny & C. Elkan, (KDD 2002)
• [3] Vergleich der probabilistischen Ausgabe von Support-Vektor-Maschinen mit normalisierten Likelihood-Methoden, J. Platt, (1999)
• [4] Vorhersage einer guten Wahrscheinlichkeit durch überwachtes Lernen, A. Niculescu-Mizil & R. Caruana, ICML 2005

[scikit-learn 0.18 Benutzerhandbuch 1. Überwachtes Lernen](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98 Von% E3% 81% 8D% E5% AD% A6% E7% BF% 92)

© 2010 - 2016, Entwickler von Scikit-Learn (BSD-Lizenz).