[PYTHON] [Übersetzung] scikit-learn 0.18 Benutzerhandbuch 4.5. Zufällige Projektion
google übersetzte http://scikit-learn.org/0.18/modules/random_projection.html [scikit-learn 0.18 Benutzerhandbuch 4. Datensatzkonvertierung](http://qiita.com/nazoking@github/items/267f2371757516f8c168#4-%E3%83%87%E3%83%BC%E3%82%BF % E3% 82% BB% E3% 83% 83% E3% 83% 88% E5% A4% 89% E6% 8F% 9B)
4.5 Zufällige Projektion
sklearn.random_projection Module sind eine kontrollierte Menge für schnellere Verarbeitungszeiten und kleinere Modellgrößen Implementiert eine einfache und rechnerisch effiziente Methode, um die Dimension der Daten zu reduzieren, indem die Genauigkeit von (als zusätzliche Varianz) gehandelt wird. Dieses Modul implementiert zwei Arten von unstrukturierten Zufallsmatrizen, die Gaußsche Zufallsmatrix und die Sparse-Zufallsmatrix. Die Abmessungen und die Verteilung der zufälligen Projektionsmatrix werden gesteuert, um den Paarabstand zwischen zwei beliebigen Stichproben im Datensatz beizubehalten. Daher ist die zufällige Projektion eine gute Approximationstechnik für entfernungsbasierte Methoden.
- Verweise:
- Sanjoy Das Gupta. Experimentieren Sie mit zufälliger Projektion. Protokoll der 16. Konferenz über die Unsicherheit der künstlichen Intelligenz (UAI'00), Craig Boutilier und Moisés Goldszmidt (Hrsg.). Morgan Kaufmann Publishers Inc., San Francisco, Kalifornien, USA, 143-151.
- Ella Bingham und Heiki Mannilla 2001 [Zufällige Projektion bei der Dimensionsreduktion: Anwendung auf Bild- und Textdaten](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.24.5135&rep=rep1&type = pdf) Vortrag auf der 7. Internationalen ACM SIGKDD-Konferenz über Wissensentdeckung und Data Mining (KDD'01) ACM, New York, NY, USA, 245-250.
4.5.1 Johnson-Lindenstrauss-Nachtrag
Das theoretische Hauptergebnis der Effizienz der Zufallsprojektion ist Johnson Lindenstrauss Supplement (zitiert Wikipedia).
In der Mathematik ist der Anhang von Johnson-Lindenstrauss das Ergebnis einer verzerrungsarmen Einbettung von Punkten in einen hoch- bis niedrigdimensionalen euklidischen Raum. Die Ergänzung besagt, dass eine kleine Menge von Punkten in einem höherdimensionalen Raum in einen viel niedrigerdimensionalen Raum eingebettet werden kann, so dass der Abstand zwischen den Punkten weitgehend erhalten bleibt. Die zum Einbetten verwendete Karte ist mindestens Lipschitz und kann auch als orthodoxe Projektion betrachtet werden.
sklearn.random_projection.johnson_lindenstrauss_min_dim Es schätzt konservativ die minimale Größe des künstlichen Unterraums und garantiert die durch zufällige Projektion verursachte begrenzte Verzerrung.
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
663
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894, 9868, 11841])
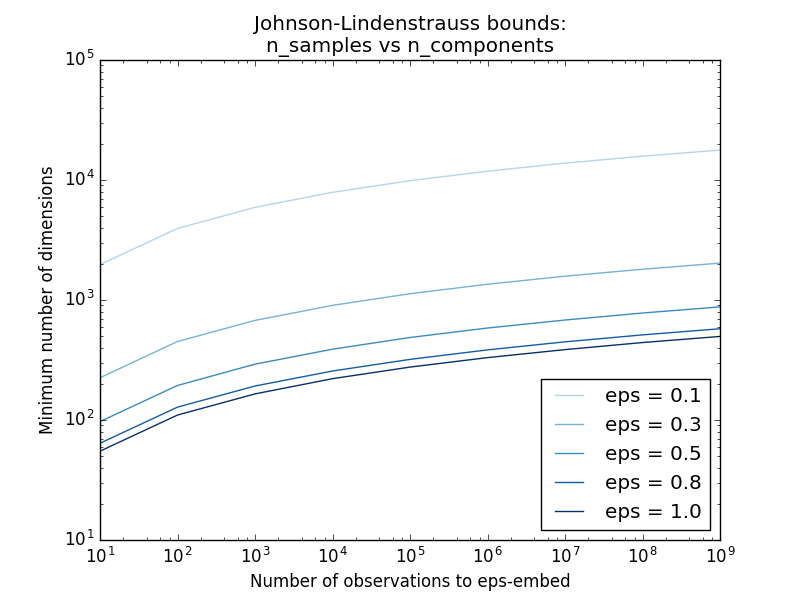
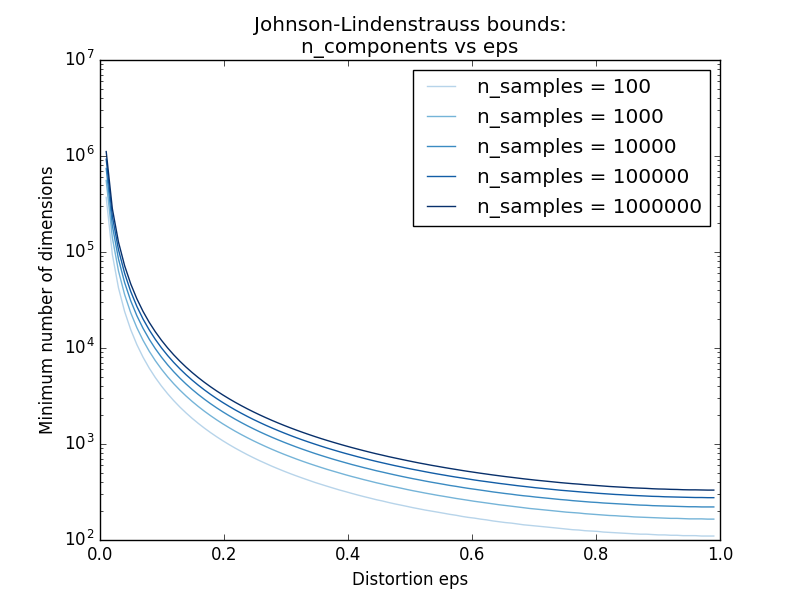
- Beispiel:
- Siehe Johnson-Lindenstrauss für theoretische Kommentare zur Agenda von Johnson-Lindenstrauss und für die Einbettung durch zufällige Projektion zur empirischen Verifizierung unter Verwendung spärlicher Zufallsmatrizen.
- Verweise:
- Sanjoy Das Gupta und Anupam Gupta, 1999. Grundlegende Beweise für die Johnson-Lindenstrauss-Ergänzung.
4.5.2. Gaußsche Zufallsprojektion
sklearn.random_projection.GaussianRandomProjection projiziert den ursprünglichen Eingaberaum auf eine zufällig generierte Matrix, um die Dimensionen zu reduzieren. Hier werden die Komponenten aus der folgenden Verteilung $ N (0, \ frac {1} {n_ {Komponenten}}) $ abgeleitet. Hier ist ein kleiner Auszug, der zeigt, wie der Gaußsche Zufallsprojektionstransformator verwendet wird:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
4.5.3. Spärliche zufällige Projektion
sklearn.random_projection.SparseRandomProjection ist die ursprüngliche Zufallsmatrix unter Verwendung einer spärlichen Zufallsmatrix Reduzieren Sie die Abmessungen, indem Sie Platz projizieren. Die Sparse Random Matrix ist eine Alternative zur dichten Gaußschen Zufallsprojektionsmatrix, die eine ähnliche Einbettungsqualität garantiert, speichereffizienter ist und eine schnelle Berechnung der projizierten Daten ermöglicht. Wenn Sie "s = 1 / Dichte" definieren, werden die Elemente der Zufallsmatrix
\left\{
\begin{array}{c c l}
-\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\
0 &\text{with probability} & 1 - 1 / s \\
+\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\
\end{array}
\right.
Dabei ist $ n_ {\ text {components}} $ die Größe des projizierten Unterraums. Standardmäßig ist die Dichte von Nicht-Null-Elementen auf die folgende von Ping Li et al. Empfohlene Mindestdichte eingestellt. $ 1 / \ sqrt {n_ {\ text {features}}} $
Ein kleiner Auszug, der zeigt, wie die Sparse Random Projection Transform verwendet wird:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100,10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
- Verweise:
- D. Achlioptas Datenbankfreundliche Zufallsprojektion: Johnson-Lindenstrauss und binäre Münzen Computer Systems Science 66 (2003) 671 & ndash; 687
- Ping Li, Trevor J. Hastie und Kenneth W. Church 2006 [Sehr spärliche zufällige Projektion](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.62.585&rep=rep1&type= pdf) Vortrag auf der 12. Internationalen ACM SIGKDD-Konferenz über Wissensentdeckung und Data Mining (KDD '06) ACM, New York, NY, USA, 287-296.
[scikit-learn 0.18 Benutzerhandbuch 4. Datensatzkonvertierung](http://qiita.com/nazoking@github/items/267f2371757516f8c168#4-%E3%83%87%E3%83%BC%E3%82%BF % E3% 82% BB% E3% 83% 83% E3% 83% 88% E5% A4% 89% E6% 8F% 9B)
© 2010 - 2016, Entwickler von Scikit-Learn (BSD-Lizenz).