[PYTHON] [Übersetzung] scikit-learn 0.18 Benutzerhandbuch 2.5. Zerlegen von Signalen in Komponenten (Matrixzerlegungsproblem)
google übersetzte http://scikit-learn.org/0.18/modules/decomposition.html
[Inhalt des Benutzerhandbuchs](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA%E3%81%97%E5 % AD% A6% E7% BF% 92)
2.5 Zerlegen Sie das Signal in der Komponente (Matrixzerlegungsproblem)
2.5.1 Hauptkomponentenanalyse (PCA)
2.5.1.1 Genaue PCA- und probabilistische Interpretation
PCA wird verwendet, um einen multivariaten Datensatz in einen Satz aufeinanderfolgender orthogonaler Komponenten zu zerlegen, die die maximale Dispersionsmenge erklären. In scikit-learn verwendet PCA die Methode fit für n Komponenten. Es ist als Transformatorobjekt implementiert, das diese Komponenten mit neuen Daten trainiert und projiziert.
Mit dem optionalen Parameter "whiten = True" können Sie Daten in einen einzelnen Raum projizieren, während Sie jede Komponente auf eine Einheitenverteilung skalieren. Dies ist oft nützlich, wenn der stromabwärtige Teil des Modells ein starkes Signal isotrop voraussetzt. Dies ist beispielsweise bei einer Support-Vektor-Maschine der Fall, die den RBF-Kernel und den K-Means-Clustering-Algorithmus verwendet.
Das Folgende ist ein Beispiel für einen Iris-Datensatz. Es besteht aus vier Merkmalen, die auf zwei Dimensionen projiziert werden, und der größte Teil der Dispersion wird beschrieben.
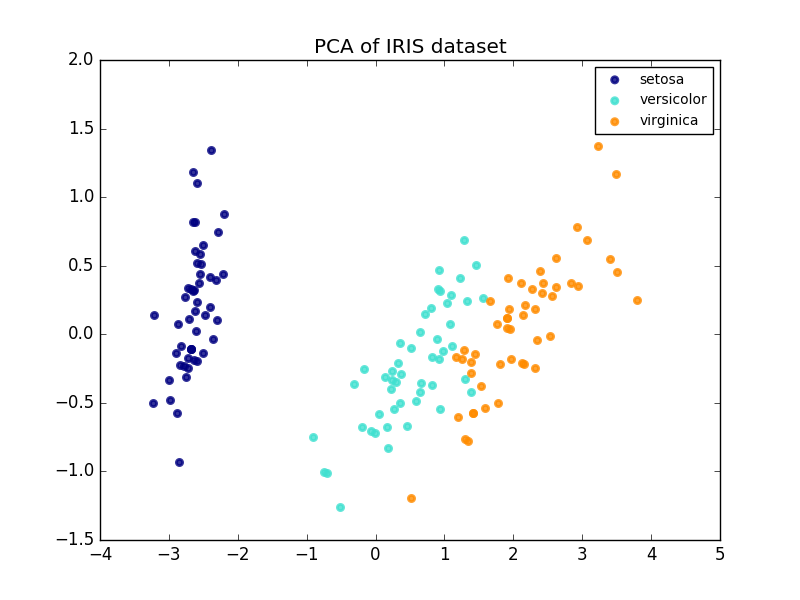
Das PCA-Objekt bietet auch eine probabilistische Interpretation der PCA, die Datenpotential basierend auf dem beschriebenen Varianzbetrag liefern kann. Auf diese Weise implementieren wir eine Bewertungsmethode, die zur gegenseitigen Authentifizierung verwendet werden kann.
- Beispiel:
- [Vergleich der LDA- und PCA-2D-Projektion des Iris-Datensatzes](http://scikit-learn.org/0.18/auto_examples/decomposition/plot_pca_vs_lda.html#sphx-glr-auto-examples-decomposition-plot-pca-vs -lda-py)
- [Modellauswahl durch probabilistische PCA- und Faktoranalyse (FA)](http://scikit-learn.org/0.18/auto_examples/decomposition/plot_pca_vs_fa_model_selection.html#sphx-glr-auto-examples-decomposition-plot-pca- vs-fa-model-selection-py)
2.5.1.2 Inkrementelle PCA
PCA Objekte sind sehr nützlich, haben jedoch bestimmte Einschränkungen für große Datenmengen. es gibt. PCA unterstützt nur die Stapelverarbeitung, daher müssen alle verarbeiteten Daten in den Hauptspeicher passen. IncrementalPCA Das Objekt verwendet eine andere Verarbeitungsform und entspricht fast dem Ergebnis von PCA. Es ermöglicht Teilberechnungen, die genau übereinstimmen, und verarbeitet die Daten im Mini-Batch-Verfahren. Mit IncrementalPCA können Sie eine Off-Core-Hauptkomponentenanalyse auf eine der folgenden Arten implementieren:
- Verwenden Sie die Methode "partial_fit "für Datenblöcke, die nacheinander von einer lokalen Festplatte oder Netzwerkdatenbank abgerufen werden.
- Rufen Sie die
fit-Methode für eine speicherabgebildete Datei mitnumpy.memmapauf.
IncrementalPCA speichert nur Schätzungen der Komponenten- und Rauschverteilung und aktualisiert "EXPLAIN_Variance_Ratio_" schrittweise. Aus diesem Grund hängt die Speichernutzung von der Anzahl der Proben pro Stapel ab, nicht von der Anzahl der vom Datensatz verarbeiteten Proben.
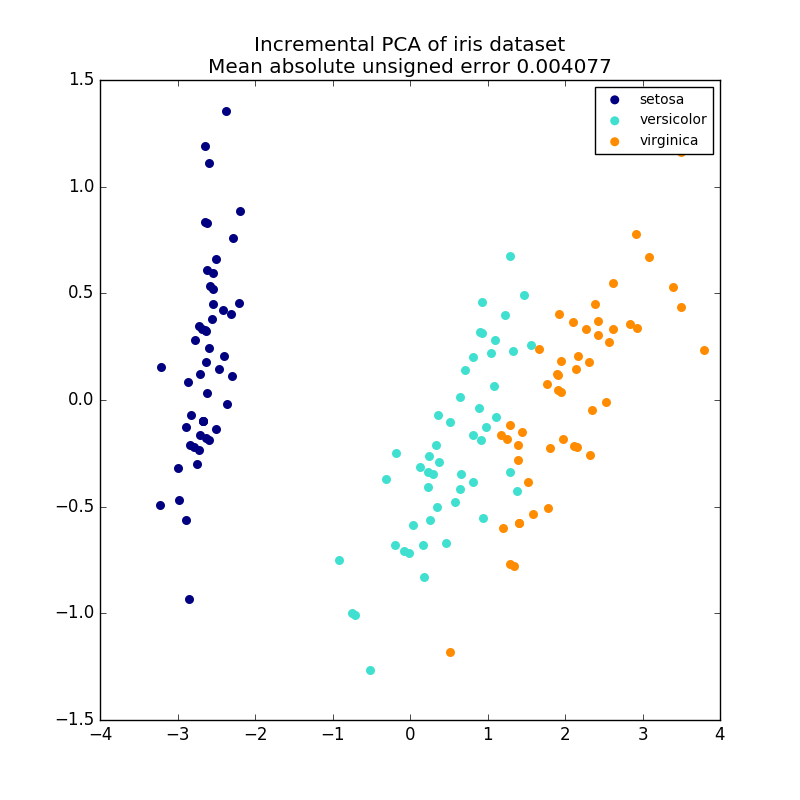
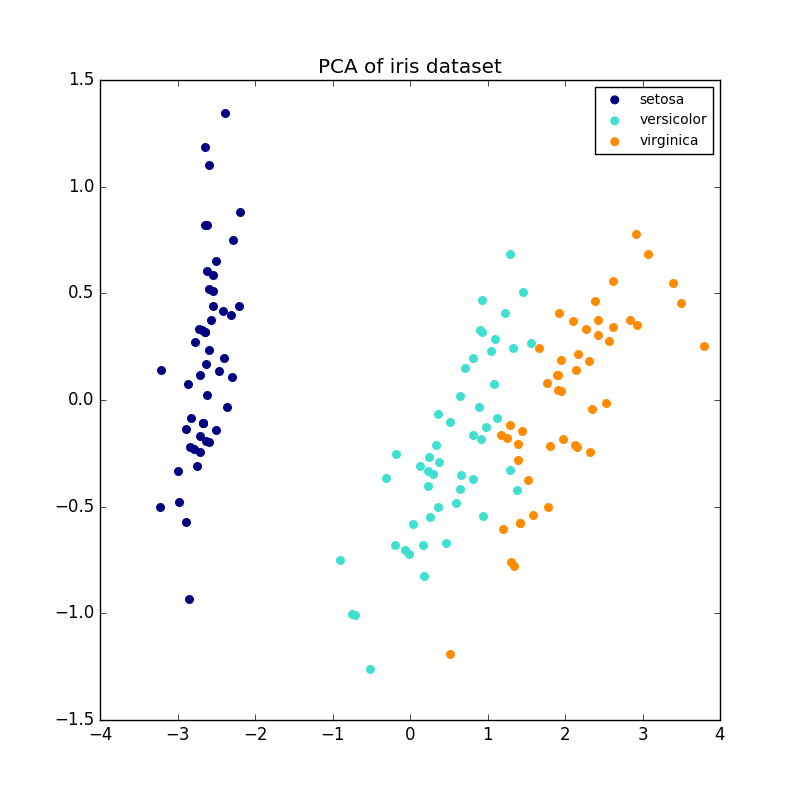
- Beispiel:
- Inkrementelle PCA
2.5.1.3. PCA mit randomisierter SVD
Es ist oft interessant, Daten in einen Raum mit niedrigeren Dimensionen zu projizieren, der die meisten Varianzen beibehält, indem der Singularitätsvektor der Komponente entfernt wird, der einem Singularitätswert zugeordnet ist. Wenn es sich beispielsweise um ein 64 x 64 Pixel großes Graustufenbild zur Gesichtserkennung handelt, beträgt die Datendimension 4096, und das Trainieren einer RBF-Unterstützungsvektormaschine für einen derart großen Datenbereich ist langsam. Darüber hinaus sind alle Bilder des menschlichen Gesichts etwas ähnlich, sodass wir sehen können, dass die Eigendimensionalität der Daten viel weniger als 4096 beträgt. Die Probe hat eine Vielzahl von viel geringeren Abmessungen (z. B. etwa 200). Der PCA-Algorithmus kann verwendet werden, um die Daten linear zu transformieren, während gleichzeitig die Dimensionen reduziert und der größte Teil der beschriebenen Varianz beibehalten wird. Die mit dem optionalen Parameter "svd_solver =" randomisiert "verwendete PCA-Klasse ist in solchen Fällen sehr nützlich. Es ist viel effizienter, die Berechnung auf ungefähre Schätzungen des Singularvektors zu beschränken, da die meisten Singularvektoren entfernt werden. Bitte führen Sie die Konvertierung tatsächlich durch. Hier sind zum Beispiel 16 Beispielporträts (zentriert um 0,0) aus dem Olivetti-Datensatz. Rechts sind die ersten 16 singulären Vektoren als Porträts rekonstruiert. Die Berechnungszeit beträgt weniger als 1 Sekunde, da nur die 16 besten Singularvektoren des Datensatzes von $ n_ {Samples} = 400 $ und $ n_ {Features} = 64 \ times 64 = 4096 $ erforderlich sind.

Hinweis: Sie müssen auch den optionalen Parameter "svd_solver =" randomisiert "verwenden, um der PCA die Größe des niedrigdimensionalen Raums" n_components "als erforderlichen Eingabeparameter zu geben.
Konzentration auf $ n_ {max} = max (n_ {Stichproben}, n_ {Merkmale}) $ und $ n_ {min} = min (n_ {Stichproben}, n_ {Merkmale}) $, die zeitliche Komplexität der randomisierten PCA Ist $ O (n_ {max} ^ 2 \ cdot n_ {min}) $ anstelle von $ O (n_ {max} ^ 2 \ cdot n_ {Komponenten}) $ in der genauen in PCA implementierten Methode. Der zufällige PCA-Speicherbedarf beträgt genau $ n_ {max} Es ist proportional zu $ 2 \ cdot n_ {max} \ cdot n_ {Komponenten} $ anstelle von \ cdot n_ {min} $. Hinweis: Die Implementierung von "inverse_transform" in PCA mit "svd_solver =" randomisiert "ist nicht die exakte Umkehrung von" transform ", selbst mit" whiten = False "(Standard).
- Beispiel:
- Beispiel für die Erkennung mit eindeutigem Gesicht und SVM
- Zerlegung von Gesichtsdatensätzen
- Verweise:
- Zufällige Strukturen finden: Wahrscheinlichkeitsalgorithmen zur Konstruktion der ungefähren Matrixzerlegung Halko et al. , 2009
2.5.1.4. Kernel-PCA
KernelPCA ist eine Erweiterung von PCA, die eine nichtlineare Dimensionsreduktion mithilfe des Kernels realisiert. (Siehe Pair Metrics, Affinity and Kernel (http://scikit-learn.org/0.18/modules/metrics.html#metrics)). Es hat viele Anwendungen wie Rauschunterdrückung, Komprimierung und strukturierte Vorhersage (Kernel-Abhängigkeitsschätzung). KernelPCA unterstützt sowohl "transform" als auch "inverse_transform".
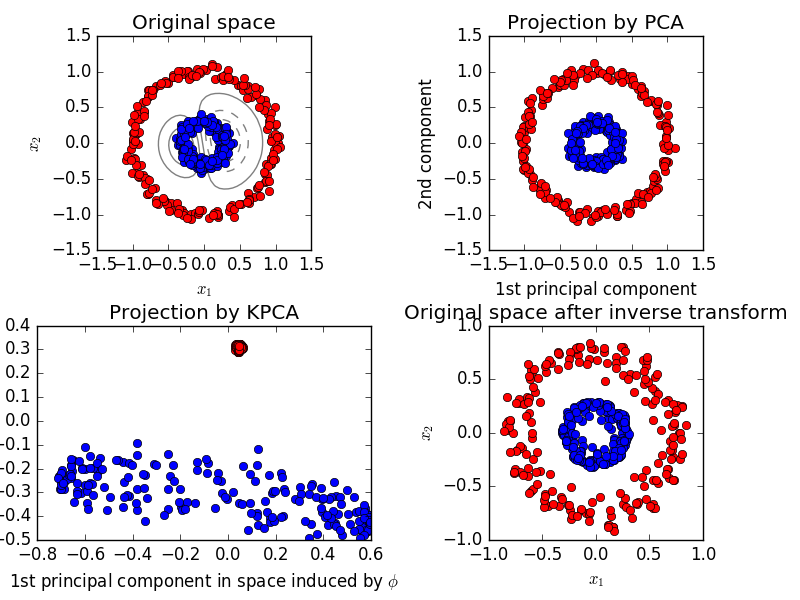
- Beispiel:
- Kernel PCA
2.5.1.5 Sparse-Hauptkomponentenanalyse (SparsePCA und MiniBatchSparsePCA)
SparsePCA extrahiert den Satz von Komponenten mit geringer Dichte, die die Daten am besten rekonstruieren. Es ist eine Variante von PCA zum Zweck von MiniBatchSparsePCA (MiniBatchSparsePCA) ist eine Variante von SparsePCA. Die Genauigkeit ist jedoch minderwertig. Die erhöhte Geschwindigkeit wird erreicht, indem kleine Teile des Funktionsumfangs für eine bestimmte Anzahl von Iterationen wiederholt werden. Die Hauptkomponentenanalyse (PCA) hat den Nachteil, dass die durch dieses Verfahren extrahierten Komponenten eine ausschließlich dichte Darstellung aufweisen, d. H. Einen Koeffizienten ungleich Null, wenn sie als lineare Kombination der ursprünglichen Variablen dargestellt werden. Dies kann schwierig zu interpretieren sein. In vielen Fällen kann die tatsächlich zugrunde liegende Komponente natürlicher als ein spärlicher Vektor vorgestellt werden. Beispielsweise können bei der Gesichtserkennung Komponenten natürlich Teilen des Gesichts zugeordnet werden. Die spärliche Hauptkomponente betont deutlich, welches der ursprünglichen Merkmale zu den Unterschieden zwischen den Stichproben beiträgt, was zu einer präziseren und interpretierbareren Darstellung führt. Das folgende Beispiel zeigt 16 Komponenten, die mit SparsePCA aus dem Olivetti-Gesichtsdatensatz extrahiert wurden. Sie können sehen, wie der Normalisierungsterm viele Nullen ableitet. Darüber hinaus macht die natürliche Struktur der Daten die Koeffizienten ungleich Null vertikal benachbart. Das Modell erzwingt dies nicht mathematisch. Jede Komponente ist ein Vektor $ h \ in \ mathbf {R} ^ {4096} $, und es gibt kein Konzept der vertikalen Nachbarschaft, außer bei menschenfreundlichen Visualisierungen wie 64 x 64 Pixel-Bildern. Die Tatsache, dass die unten gezeigten Komponenten lokal angezeigt werden, ist ein Effekt der eindeutigen Struktur der Daten, und solche lokalen Muster minimieren Rekonstruktionsfehler. Es gibt Normen, die unter Berücksichtigung der Nachbarschaft und verschiedener Arten von Strukturen zu Spärlichkeit führen. Siehe [Jen09] für eine Übersicht über solche Methoden. Weitere Informationen zur Verwendung von Sparse PCA finden Sie im folgenden Beispielabschnitt.

Beachten Sie, dass das SparsePCA-Problem viele verschiedene Ausdrücke enthält. Was hier implementiert wird, basiert auf [Mrl09]. Das gelöste Optimierungsproblem ist das PCA-Problem (Wörterbuchlernen), das eine $ \ ell_1 $ Strafe für die Komponente hat.
(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2}
||X-UV||_2^2+\alpha||V||_1 \\
\text{subject to\,} & ||U_k||_2 = 1 \text{ for all }
0 \leq k < n_{components}
Die $ \ ell_1 $ -Norm, die zu Spärlichkeit führt, schützt die Lernkomponente auch vor Rauschen, wenn nur wenige Trainingsmuster verfügbar sind. Der Grad der Strafe (und damit die Spärlichkeit) kann über den Hyperparameter "alpha" eingestellt werden. Kleine Werte führen zu einem lose regulierten Factoring, und große Werte reduzieren viele Koeffizienten auf Null.
** Hinweis: ** Im Online-Algorithmus lautet die Klasse MiniBatchSparsePCA `teilweise_fit Es wird nicht implementiert, da der Algorithmus entlang der Merkmalsrichtung und nicht entlang der Abtastrichtung online ist.
- Beispiel:
- Decomposition Face Dataset
- Verweise:
- \ [Mrl09] Online-Wörterbuchlernen für spärliche Codierung J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009
- \ [Jen09] Strukturierte spärliche Hauptkomponentenanalyse R. Jenatton, G. Obozinski F. Bach, 2009
2.5.2 Zerlegung der Kürzungssingularität und latente semantische Analyse
TruncatedSVD hat $ k $, dessen $ k $ ein benutzerdefinierter Parameter ist. Implementiert eine Variante der Singularity Decomposition (SVD), die nur die maximale Singularität von berechnet. Wenn die abgeschnittene SVD auf eine Termdokumentmatrix angewendet wird (von "CountVectorizer" oder "TfidfVectorizer" zurückgegeben), ist diese Transformation [latente semantische Analyse (LSA)](http: //nlp.stanford). Bekannt als .edu / IR-book / pdf / 18lsi.pdf). Dies dient dazu, die Matrix in einen niederdimensionalen "semantischen" Raum umzuwandeln. Insbesondere ist bekannt, dass LSAs die Auswirkungen von Synonymen und Polynomien bekämpfen (beide bedeuten im Großen und Ganzen mehrere Bedeutungen). Dies weist darauf hin, dass der Begriff Dokumentmatrix zu dünn ist und eine geringe Ähnlichkeit durch Mittel wie Kosinusähnlichkeit aufweist.
** Hinweis: ** LSA, auch als Latent Indexing (LSI) bezeichnet, wird ausschließlich für persistente Indizes zum Abrufen von Informationen verwendet.
Mathematisch ergibt die abgeschnittene SVD, die auf das Trainingsmuster $ X $ angewendet wird, eine Annäherung mit niedrigem Rang $ X $.
X \approx X_k = U_k \Sigma_k V_k^\top
Nach dieser Operation ist $ U_k \ Sigma_k ^ \ top $ ein transformierter Trainingssatz mit $ k $ -Funktionen (in der API als "n_components" bezeichnet). Es multipliziert auch $ V_k $, um die Testmenge $ X $ zu konvertieren.
X' = X V_k
** Hinweis: ** Der größte Teil der LSA-Verarbeitung in der Literatur zu Natural Language Processing (NLP) und Information Retrieval (IR) vertauscht die Achsen der Matrix $ n $ so, dass sie die Form "n_features x n_samples" hat. Ich werde. Wir präsentieren die LSA auf verschiedene Arten, die gut zur Scicit-Learn-API passen, aber die gefundenen Singularitäten sind dieselben.
TruncatedSVD ist PCA sehr ähnlich, außer dass es direkt auf der Beispielmatrix $ X $ anstelle der kovarianten Matrix funktioniert. Subtrahiert man den Durchschnitt von $ X $ in Spaltenrichtung (pro Merkmal) von der Merkmalsmenge, entspricht die resultierende abgeschnittene SVD in der Matrix der PCA. In der Praxis verdichtet dies die "scipy.sparse" -Matrix nicht, da der Truncated SVD-Konverter selbst für mittelgroße Dokumentensammlungen Speicher füllen kann. Mittel zu akzeptieren.
Der TruncatedSVD-Konverter funktioniert mit jeder (spärlichen) Feature-Matrix. Die Verwendung mit der tf-idf-Matrix wird jedoch gegenüber der nicht verarbeiteten Häufigkeit in den LSA- / Dokumentverarbeitungseinstellungen empfohlen. Um die falschen Annahmen von LSA zu Textdaten auszugleichen, sollten insbesondere die sublineare Skalierung und die inverse Dokumenthäufigkeit aktiviert werden, um die Merkmalswerte näher an die Gaußsche Verteilung heranzuführen (sublinear_tf = True, use_idf = Richtig).
- Beispiel:
- Clustering von Textdokumenten mit k-means
- Verweise:
- Christopher D. Manning, Prabhakar Raghavan und Hinrich Schütze (2008), Cambridge University Press, Kapitel 18: Matrixzerlegung und latente semantische Indexierung .pdf)
2.5.3 Wörterbuch lernen
2.5.3.1. Sparsame Codierung mit vorberechnetem Wörterbuch
SparseCoder Das Objekt ist ein festes vorberechnetes Signal, z. B. eine diskrete Wavelet-Basis. Ein Schätzer, der zum Konvertieren in spärliche lineare Verknüpfungen aus einem Wörterbuch verwendet werden kann. Daher implementiert dieses Objekt die "fit" -Methode nicht. Diese Konvertierung wird zu einem spärlichen Codierungsproblem. Finden einer Darstellung der Daten als lineare Verknüpfung von möglichst wenigen Wörterbuchatomen. Alle Variationen des Wörterbuchlernens implementieren die folgenden Transformationsmethoden, die über den Initialisierungsparameter "transform_method" gesteuert werden können.
- Streben nach orthogonalem Matching (OMP: Orthogonal Matching Pursuit)
- Minimale Winkelregression (Minimale Winkelregression)
- Lasso berechnet durch minimale Winkelregression
- Lasso mit Koordinatenabstieg (Lasso) (Lasso)
- Schwelle
Die Schwellenwerte sind sehr schnell, können jedoch nicht genau rekonstruiert werden. Sie haben sich in der Literatur als nützlich für Klassifizierungsarbeiten erwiesen. Für Bildrekonstruktionsaufgaben bietet die orthogonale Übereinstimmungsverfolgung die genaueste und unvoreingenommenste Rekonstruktion. Das Wörterbuch-Lernobjekt bietet die Möglichkeit, positive und negative Werte im Ergebnis einer spärlichen Codierung über den Parameter "split_code" zu trennen. Dies ist ein Wörterbuchtraining zum Extrahieren der für das überwachte Lernen verwendeten Funktionen, damit der Lernalgorithmus unterschiedliche Gewichte von positiven zu negativen Lasten zuweisen kann, die den negativen Lasten eines bestimmten Atoms entsprechen. Dies ist nützlich bei der Verwendung. Der Split-Code für ein Beispiel hat eine Länge von "2 * n_components" und wird nach den folgenden Regeln erstellt: Zunächst wird der normale Code der Länge "n_components" berechnet. Der erste Eintrag "n_components" für "split_code" wird dann mit dem positiven Teil des regulären Codevektors gefüllt. Die zweite Hälfte des geteilten Codes wird mit dem negativen Teil des Codevektors mit nur positiven Vorzeichen gefüllt. Daher ist "split_code" nicht negativ.
2.5.3.2 Allgemeines Wörterbuchlernen
Das Lernen von Wörterbüchern (DictionaryLearning) dient dazu, übereinstimmende Daten nur spärlich zu codieren. Es ist ein Matrixzerlegungsproblem, das dem Finden eines (normalerweise übermäßigen) Wörterbuchs entspricht, das gut funktioniert. Die Darstellung der Daten als verdünnte Kombination von Atomen aus dem übervollständigen Wörterbuch legt die Arbeit der wichtigsten Gesichtsfelder von Säugetieren nahe. Infolgedessen hat sich gezeigt, dass das auf Bildfeldern angewendete Wörterbuchlernen gute Ergebnisse bei Bildverarbeitungsaufgaben wie Bildvervollständigung, Reparatur und Rauschentfernung sowie bei überwachten Erkennungsaufgaben liefert. Das Lernen von Wörterbüchern ist ein Optimierungsproblem, das gelöst wird, indem der Sparse-Code auf alternative Weise aktualisiert und das Wörterbuch so geändert wird, dass es als Lösung für das Multiple-Lasso-Problem am besten zum Sparse-Code passt. ..
(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2}
||X-UV||_2^2+\alpha||U||_1 \\
\text{subject to\,} & ||V_k||_2 = 1 \text{ for all }
0 \leq k < n_{atoms}


Nach der Anpassung an ein Wörterbuch mithilfe dieser Schritte ist die Transformation ein einfacher Codierungsschritt, der dieselbe Implementierung mit allen Wörterbuchlernobjekten teilt (sparsame Codierung mit vorberechneten Wörterbüchern (http: //)). Siehe scikit-learn.org/0.18/modules/decomposition.html#sparsecoder). Das folgende Bild zeigt, wie das Wörterbuch aus einem 4x4-Pixel-Bildfeld trainiert wurde, das aus einem Teil des Bildes des Gesichts des Raigmas extrahiert wurde.

- Beispiel:
- Entfernen von Bildrauschen mithilfe des Wörterbuchlernens
- Verweise:
- "Lernen eines Online-Wörterbuchs für spärliche Codierung" J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009
2.5.3.3 Mini-Batch-Wörterbuch lernen
MiniBatchDictionaryLearning ist ein schnellerer Algorithmus zum Lernen von Wörterbüchern, der für große Datenmengen geeignet ist. Es wird jedoch eine weniger genaue Version implementiert. Standardmäßig unterteilt MiniBatchDictionaryLearning die Daten in Mini-Batch und optimiert sie online, indem der Mini-Batch eine bestimmte Anzahl von Iterationen verteilt. Derzeit wird jedoch kein gestoppter Status implementiert. Der Schätzer implementiert auch "partielle Anpassung". Dadurch wird das Wörterbuch nur einmal in einem Mini-Batch aktualisiert. Dies kann für das Online-Lernen verwendet werden, wenn die Daten von Anfang an nicht sofort verfügbar sind oder wenn die Daten nicht in den Speicher passen.
** Clustering für das Lernen von Wörterbüchern **
Beachten Sie, dass Clustering ein guter Proxy für das Lernen von Wörterbüchern sein kann, wenn das Lernen von Wörterbüchern zum Extrahieren von Ausdrücken verwendet wird (z. B. im Fall einer spärlichen Codierung). Beispiel: MiniBatchKMeans Der Schätzer ist rechnerisch effizient und die Methode "partielle Anpassung" Führen Sie Online-Lernen mit.
- Beispiel: Online-Lernen des Gesichtsteilwörterbuchs -py)

2.5.4. Faktoranalyse
Beim unbeaufsichtigten Lernen lautet der Datensatz $ X = \ {x_1, x_2, \ dots, x_n Es gibt nur } $. Wie kann dieser Datensatz mathematisch beschrieben werden? In einem sehr einfachen Modell mit kontinuierlichen latenten Variablen ist $ X $
x_i = W h_i + \mu + \epsilon
Der Vektor $ h \ _i $ wird nicht beobachtet und wird daher als "latent" bezeichnet. $ ε $ wird als Rauschausdruck betrachtet, der gemäß einer Gaußschen Verteilung mit dem Mittelwert 0 und der Kovarianz $ \ Psi $ (dh $ \ epsilon \ sim \ mathcal {N} (0, \ Psi)) $) verteilt wird. $ μ $ ist ein beliebiger Versatzvektor. Ein solches Modell wird als "generativ" bezeichnet, da es beschreibt, wie $ x \ _i $ aus $ h \ _i $ generiert wird. Verwenden aller $ x \ _i $ als Spalten zum Erstellen der Matrix $ \ mathbf {X} $ und aller $ h_i $ als Spalten in der Matrix $ \ mathbf {H} $ (gut definiert) Sie können wie folgt schreiben (mit $ \ mathbf {M} $ und $ \ mathbf {E} $):
\mathbf{X} = W \mathbf{H} + \mathbf{M} + \mathbf{E}
Mit anderen Worten, wir haben die Matrix $ \ mathbf {X} $ zerlegt. Bei $ h_i $ bedeutet die obige Gleichung automatisch die folgende probabilistische Interpretation:
p(x_i|h_i) = \mathcal{N}(Wh_i + \mu, \Psi)
Für das perfekte Wahrscheinlichkeitsmodell benötigen wir auch eine vorherige Verteilung für die latente Variable $ h $. Die einfachste Annahme, die auf den guten Eigenschaften der Gaußschen Verteilung basiert, ist $ h \ sim \ mathcal {N} (0, \ mathbf {I}) $. Dies erzeugt eine Gaußsche Verteilung als Randverteilung von $ x $:
p(x) = \mathcal{N}(\mu, WW^T + \Psi)
Ohne weitere Annahmen wäre die Idee, die latente Variable $ h $ zu haben, überflüssig. $ x $ kann vollständig mit Mittelwert und Kovarianz modelliert werden. Wir müssen einem dieser beiden Parameter eine spezifischere Struktur auferlegen. Eine einfache zusätzliche Annahme betrifft die Struktur der Fehlerkovarianz $ \ Psi $:
- $ \ Psi = \ sigma ^ 2 \ mathbf {I} $: Diese Annahme führt zu einem probabilistischen Modell der PCA.
- $ \ Psi = diag (\ psi_1, \ psi_2, \ dots, \ psi_n) $: Dieses Modell ist ein klassisches statistisches Modell. Faktoranalyse Faktoranalyse Es heißt /generated/sklearn.decomposition.FactorAnalysis.html#sklearn.decomposition.FactorAnalysis). Die Matrix W wird manchmal als "Faktorladematrix" bezeichnet.
Beide Modelle schätzen im Wesentlichen eine Gaußsche Verteilung mit einer Kovarianzmatrix mit niedrigem Rang. Beide Modelle sind probabilistisch und können in komplexere Modelle integriert werden. Zum Beispiel eine Kombination von Faktoranalysen. Sehr unterschiedliche Modelle (z. B. FastICA, wenn nicht-Gaußsche vorherige Wahrscheinlichkeiten für latente Variablen angenommen werden .decomposition.FastICA)) erhalten wird. Die Faktorenanalyse fügt eine ähnliche Komponente (die Spalte in ihrer Ladematrix) in [PCA] ein (http://scikit-learn.org/0.18/modules/generated/sklearn.decomposition.PCA.html#sklearn.decomposition.PCA). Kann generiert werden. Eine allgemeine Beschreibung dieser Komponenten ist jedoch nicht möglich (z. B. ob sie orthogonal sind oder nicht).


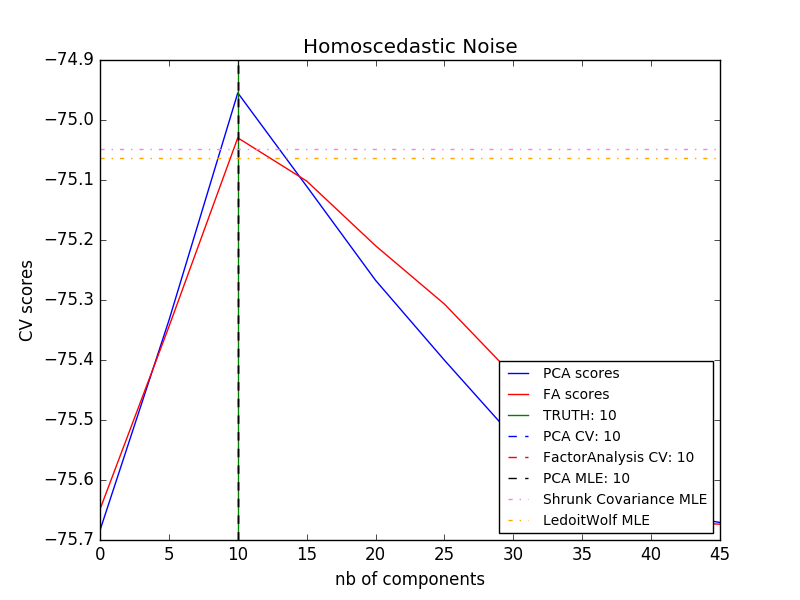
Der Hauptvorteil der Faktoranalyse gegenüber PCA liegt in allen Richtungen des Eingaberaums. Die Fähigkeit, die Dispersion individuell zu modellieren (heteroskedastisches Rauschen).

Dies ermöglicht eine bessere Modellauswahl als probabilistische PCA bei anisotropem Rauschen.
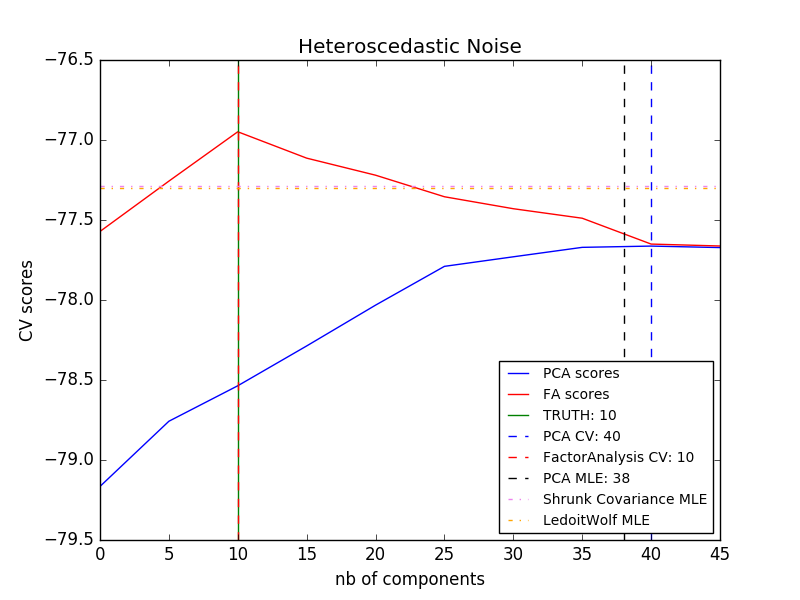
- Beispiel:
- [Modellauswahl durch probabilistische PCA- und Faktoranalyse (FA)](http://scikit-learn.org/0.18/auto_examples/decomposition/plot_pca_vs_fa_model_selection.html#sphx-glr-auto-examples-decomposition-plot-pca- vs-fa-model-selection-py)
2.5.5 Unabhängige Komponentenanalyse (ICA)
Die unabhängige Komponentenanalyse trennt multivariate Signale in maximal unabhängige additive Unterkomponenten. FastICA Implementiert in scikit-learn unter Verwendung des Algorithmus. Typischerweise wird ICA verwendet, um überlagerte Signale zu trennen, nicht um die Dimensionalität zu verringern. Das ICA-Modell enthält keinen Rauschbegriff, daher muss eine Aufhellung angewendet werden, damit das Modell korrekt ist. Dies kann intern mithilfe des Whiten-Arguments oder manuell mithilfe von PCA oder einer seiner Varianten erfolgen. Es wird klassisch verwendet, um gemischte Signale zu trennen (ein Problem, das als blinde Schallquellentrennung bezeichnet wird), wie im folgenden Beispiel.
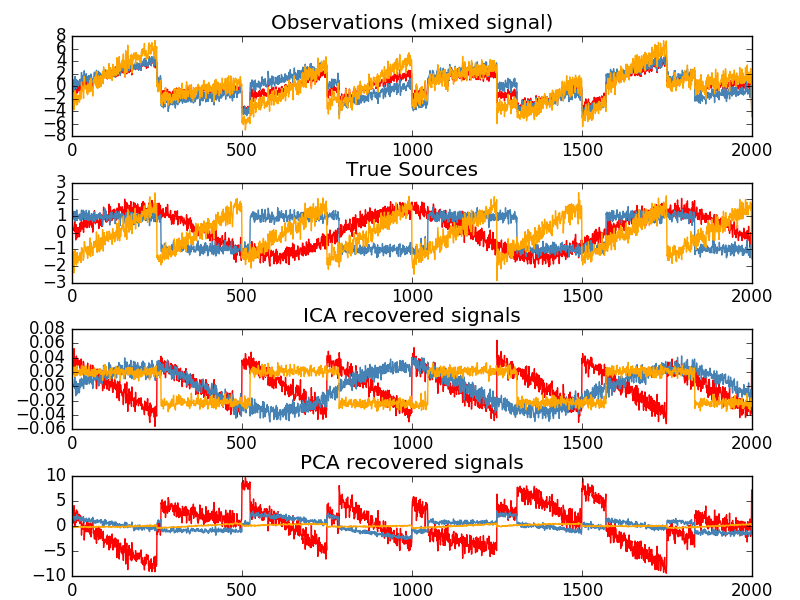
Die ICA kann auch als eine weitere nichtlineare Zerlegung verwendet werden, bei der spärliche Komponenten gefunden werden.


- Beispiel:
- [Trennung von blinden Quellen mit FastICA](http://scikit-learn.org/0.18/auto_examples/decomposition/plot_ica_blind_source_separation.html#sphx-glr-auto-examples-decomposition-plot-ica-blind-source- Trennungs-py)
- 2D-Punktgruppe FastICA
- Zerlegung von Gesichtsdatensätzen
2.5.6 Nicht negative Matrixzersetzung (NMF oder NNMF)
2.5.6.1. NMF mit Frobenius-Norm
NMF ist eine Zerlegung, bei der davon ausgegangen wird, dass die Daten und Komponenten nicht negativ sind. Ein alternativer Ansatz. Wenn die Datenmatrix keine negativen Werte enthält, können Sie NMF anstelle von PCA oder seinen Varianten einfügen. Durch Optimieren des Abstands $ d $ zwischen $ X $ und dem Matrixprodukt $ WH $ finden wir die Zerlegung der Stichprobe $ X $ in zwei nicht negative Elemente, $ W $ und $ H $. Die am weitesten verbreitete Distanzfunktion ist die quadratische Frobenius-Norm, die eine offensichtliche Erweiterung der euklidischen Distanzmatrix darstellt.
d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{\mathrm{Fro}}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2
Im Gegensatz zu PCA wird die Darstellung des Vektors additiv erhalten, indem die Komponenten ohne Subtraktion überlagert werden. Ein solches additives Modell ist nützlich für die Darstellung von Bildern und Text.
In [Hoyer, 04] wurde beobachtet, dass NMF eine teilebasierte Darstellung eines Datensatzes erzeugt, die bei sorgfältiger Einschränkung ein interpretierbares Modell liefert. Das folgende Beispiel zeigt 16 verdünnte Komponenten, die von NMA im Vergleich zu einer PCA-spezifischen Oberfläche aus einem Bild des Olivetti-Gesichtsdatensatzes gefunden wurden.

 Das Attribut
Das Attribut init bestimmt, welche Initialisierungsmethode angewendet wird. Dies hat erhebliche Auswirkungen auf die Methodenleistung. NMF implementiert die nicht negative Doppel-Singularitäts-Zerlegungsmethode (NNDSVD). NNDSVD basiert auf zwei SVD-Prozessen, die sich der Datenmatrix annähern, und die anderen ähnlichen positiven Abschnitte des resultierenden partiellen SVD-Koeffizienten nutzen die algebraische Natur der Einheitsrangmatrix. Der grundlegende NNDSVD-Algorithmus eignet sich für die Zerlegung von Sparse-Faktoren. Für eine hohe Dichte werden die Varianten NNDSVDa (alle Nullen werden gleich dem Durchschnitt aller Elemente der Daten gesetzt) und NNDSVDar (wobei Null eine zufällige Störung ist, die kleiner ist als der Durchschnitt der Daten geteilt durch 100). Wird eingestellt auf) wird empfohlen.
NMF kann auch mit einer richtig skalierten zufälligen nicht negativen Matrix initialisiert werden, indem "init =" random "gesetzt wird. Sie können auch einen ganzzahligen Startwert oder "RandomState" an "random_state" übergeben, um die Reproduzierbarkeit zu steuern.
Mit NMF können Sie der Verlustfunktion L1- und L2-Funktionen hinzufügen, um das Modell zu normalisieren. L2 Prior verwendet die Frobenius-Norm und L1 Prior verwendet die Elementeinheit L1-Norm. Wie bei ElasticNet wird die Kombination von L1 und L2 durch den Parameter "l1_ratio" ($ \ rho
\alpha \rho ||W||_1 + \alpha \rho ||H||_1
+ \frac{\alpha(1-\rho)}{2} ||W||_{Fro} ^ 2
+ \frac{\alpha(1-\rho)}{2} ||H||_{Fro} ^ 2
Die normalisierte Zielfunktion ist:
\frac{1}{2}||X - WH||_{Fro}^2
+ \alpha \rho ||W||_1 + \alpha \rho ||H||_1
+ \frac{\alpha(1-\rho)}{2} ||W||_{Fro} ^ 2
+ \frac{\alpha(1-\rho)}{2} ||H||_{Fro} ^ 2
NMF normalisiert sowohl W als auch H. Die Funktion non_negative_factorization hat eine feine Kontrolle über Normalisierungsattribute und kann nur W, H oder beides normalisieren.
- Beispiel:
- Zerlegung von Gesichtsdatensätzen
- [Themenextraktion unter Verwendung einer nicht-negativen Matrixfaktorzerlegung und potenzieller Jilliclet-Zuweisung](http://scikit-learn.org/0.18/auto_examples/applications/topics_extraction_with_nmf_lda.html#sphx-glr-auto-examples-applications-topics- Extraktion mit nmf-lda-py)
- Verweise:
- "Lernen des Teils eines Objekts durch nicht negative Matrixzerlegung" D. Lee, S. Seung, 1999
- "Faktorzerlegung einer nicht negativen Matrix mit Spärlichkeitsbeschränkung" P. Hoyer, 2004
- "Projektionsgradientenmethode für nicht negative Matrixzerlegung" C.-J. Lin, 2007
- "SVD-basierte Initialisierung: Beginn der nicht negativen Matrixzerlegung" C. Boutsidis, E. Gallopoulos, 2008
- "Schneller lokaler Algorithmus für die nicht negative Matrix- und Tensorzerlegung in großem Maßstab" A. Cichocki, P. Anh-Huy, 2009
2.5.7. Potenzielle Richtungszuweisungsmethode (LDA)
Die Latent Dirichlet Allocation ist ein generatives Wahrscheinlichkeitsmodell zum Sammeln diskreter Datensätze wie Textkorpora. Es ist auch das Themenmodell, mit dem abstrakte Themen aus einer Sammlung von Dokumenten ermittelt werden. Das grafische LDA-Modell ist ein dreistufiges Beckenmodell.
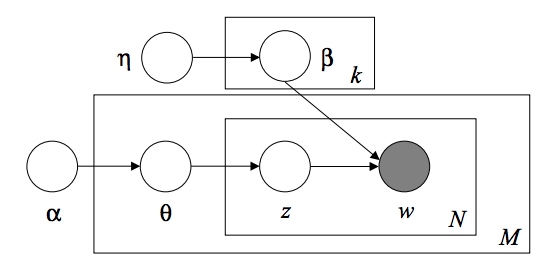
Bei der Modellierung eines Textkorpus geht das Modell von dem folgenden Generierungsprozess für einen Korpus mit einem D-Dokument und einem K-Thema aus.
- Für jedes Thema $ k $, $ \ beta_k \ sim Dirichlet (\ eta), : k = 1 ... K $
- Für jedes Dokument $ d $, $ \ theta_d \ sim Dirichlet (\ alpha), : d = 1 ... D $
- Für jedes Wort $ i $ im Dokument $ d $:
- Zeichnen Sie den Themenindex $ z_ {di} \ sim Multinomial (\ theta_d) $
- Stellen Sie das beobachtete Wort $ w_ {ij} \ sim Multinomial (beta_ {z_ {di}}.) $ Dar
Für die Parameterschätzung ist die posteriore Verteilung wie folgt:
p(z, \theta, \beta |w, \alpha, \eta) =
\frac{p(z, \theta, \beta|\alpha, \eta)}{p(w|\alpha, \eta)}
Da der Rücken umständlich ist, verwendet die Variante der Bayes'schen Variante eine einfachere Verteilung, um $ q (z, \ theta, \ beta | \ lambda, \ phi, \ gamma) $ und ihre Variantenparameter $ \ zu approximieren Lambda, \ phi, \ gamma $ sind optimiert, um die Evidence Lower Bound (ELBO) zu maximieren.
log\: P(w | \alpha, \eta) \geq L(w,\phi,\gamma,\lambda) \overset{\triangle}{=}
E_{q}[log\:p(w,z,\theta,\beta|\alpha,\eta)] - E_{q}[log\:q(z, \theta, \beta)]
Das Maximieren von ELBO ist ein Kullback-Leibler zwischen $ q (z, \ theta, \ beta) $ und echtem posterioren $ p (z, \ theta, \ beta | w, \ alpha, \ eta) $ Entspricht der Minimierung des Unterschieds in (KL).
LatentDirichletAllocation implementiert den Online-Varianten-Bayes-Algorithmus für Online- und Batch-Updates. Unterstützt beide Methoden. Die Batch-Methode aktualisiert die Variablenvariable, nachdem jeder vollständige Pfad zu den Daten übergeben wurde, während die Online-Methode die Variablenvariable vom Mini-Batch-Datenpunkt aus aktualisiert. ** Hinweis: ** Die Online-Methode konvergiert garantiert zum lokalen optimalen Punkt. Die Qualität und Geschwindigkeit der Konvergenz des optimalen Punkts kann jedoch von der Größe des Mini-Batches und den Attributen abhängen, die mit der Einstellung der Lerngeschwindigkeit verbunden sind. Wenn LatentDirichletAllocation auf die Matrix "Document-Terms" angewendet wird, wird die Matrix in eine Matrix "Topic-Terms" und eine Matrix "Document-Topic" unterteilt. Die Matrix "Themenbegriffe" wird im Modell als "Komponenten_" gespeichert, Sie können jedoch die Matrix "Dokumentthemen" mit der Methode "Transformation" berechnen. LatentDirichletAllocation implementiert auch die Methode "partial_fit ". Dies wird verwendet, wenn Daten kontinuierlich abgerufen werden.
- Beispiel:
- [Themenextraktion unter Verwendung einer nicht-negativen Matrixfaktorzerlegung und potenzieller Jilliclet-Zuweisung](http://scikit-learn.org/0.18/auto_examples/applications/topics_extraction_with_nmf_lda.html#sphx-glr-auto-examples-applications-topics- Extraktion mit nmf-lda-py)
- Verweise:
- Potenzielle Richtungszuweisungsmethode D. Bray, A. N., M. Jordan, 2003
- Online-Lernen für eine mögliche Methode zur Zuweisung von Direktionen M. Hoffman, D.Blei, F.Bach, 2010
- Probabilistic Variant Inference M. Hoffman, D. Blei, C. Wang, J. Pasley, 2013
[Inhalt des Benutzerhandbuchs](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA%E3%81%97%E5 % AD% A6% E7% BF% 92)
© 2010 - 2016, Entwickler von Scikit-Learn (BSD-Lizenz).
Recommended Posts