[PYTHON] [Übersetzung] scikit-learn 0.18 Benutzerhandbuch 3.3. Modellbewertung: Quantifizieren Sie die Qualität der Vorhersage

google übersetzte http://scikit-learn.org/0.18/modules/model_evaluation.html [scikit-learn 0.18 Benutzerhandbuch 3. Modellauswahl und -bewertung](http://qiita.com/nazoking@github/items/267f2371757516f8c168#3-%E3%83%A2%E3%83%87%E3%83] Von% AB% E3% 81% AE% E9% 81% B8% E6% 8A% 9E% E3% 81% A8% E8% A9% 95% E4% BE% A1)

3.3. Modellbewertung: Quantifizieren Sie die Qualität der Vorhersagen

Es gibt drei verschiedene Ansätze zur Bewertung der Qualität von Modellvorhersagen.

Schließlich sind Dummy-Evaluatoren nützlich, um Basiswerte für diese Metriken für die zufällige Vorhersage zu erhalten.

3.3.1 Bewertungsparameter: Definition der Modellbewertungsregeln

model_selection.GridSearchCV und [model_selection.cross_val_score](http: // scikit-learn) Für die Modellauswahl und -bewertung mithilfe von Tools wie .org / 0.18 / modules / generate / sklearn.model_selection.cross_val_score.html # sklearn.model_selection.cross_val_score), dem Parameter "Scoring", der die auf die Metriken angewendeten Metriken steuert Benutzen.

3.3.1.1 Allgemeiner Fall: Vordefinierter Wert

Für die häufigsten Anwendungsfälle können Sie den Parameter "Scoring" verwenden, um ein Scoring-Objekt anzugeben. Die folgende Tabelle zeigt alle möglichen Werte. Alle Scorer-Objekte folgen der Regel, dass ** höhere Rückgabewerte besser sind als niedrigere Rückgabewerte **. Daher der Abstand zwischen dem Modell und den Daten, z. B. metrik.mean_squared_error Die von Ihnen gemessene Metrik ist als neg_mean_squared_error verfügbar, der den negativen Wert der Metrik zurückgibt.

Scoring Function Comment
Einstufung
‘accuracy’ metrics.accuracy_score
‘average_precision’ metrics.average_precision_score
‘f1’ metrics.f1_score Für binäre Ziele
‘f1_micro’ metrics.f1_score Mikro-Mittelung
‘f1_macro’ metrics.f1_score Makro-Mittelung
‘f1_weighted’ metrics.f1_score gewichteter Durchschnitt
‘f1_samples’ metrics.f1_score Multi-Label-Probe
‘neg_log_loss’ metrics.log_loss predict_probaBrauche Unterstützung
‘precision’ etc. metrics.precision_score Das Suffix lautet'f1'Gilt genauso wie.
‘recall’ etc. metrics.recall_score Das Suffix lautet'f1'Gilt genauso wie.
‘roc_auc’ metrics.roc_auc_score
Clustering
‘adjusted_rand_score’ metrics.adjusted_rand_score
Rückkehr
‘neg_mean_absolute_error’ metrics.mean_absolute_error
‘neg_mean_squared_error’ metrics.mean_squared_error
‘neg_median_absolute_error’ metrics.median_absolute_error
‘r2’ metrics.r2_score

Usage examples:

>>>
>>> from sklearn import svm, datasets
>>> from sklearn.model_selection import cross_val_score
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> clf = svm.SVC(probability=True, random_state=0)
>>> cross_val_score(clf, X, y, scoring='neg_log_loss') 
array([-0.07..., -0.16..., -0.06...])
>>> model = svm.SVC()
>>> cross_val_score(model, X, y, scoring='wrong_choice')
Traceback (most recent call last):
ValueError: 'wrong_choice' is not a valid scoring value. Valid options are ['accuracy', 'adjusted_rand_score', 'average_precision', 'f1', 'f1_macro', 'f1_micro', 'f1_samples', 'f1_weighted', 'neg_log_loss', 'neg_mean_absolute_error', 'neg_mean_squared_error', 'neg_median_absolute_error', 'precision', 'precision_macro', 'precision_micro', 'precision_samples', 'precision_weighted', 'r2', 'recall', 'recall_macro', 'recall_micro', 'recall_samples', 'recall_weighted', 'roc_auc']

3.3.1.2. Definieren von Bewertungsstrategien aus metrischen Funktionen

Das Modul sklearn.metric stellt auch eine Reihe einfacher Funktionen zur Verfügung, die Messwerte und vorhergesagte Vorhersagefehler bei einer Vorhersage messen:

Für viele Metriken sind möglicherweise zusätzliche Parameter erforderlich, z. B. fbeta_score. Daher gibt es keinen Namen, der als Bewertungswert verwendet werden könnte. In solchen Fällen müssen Sie ein geeignetes Bewertungsobjekt generieren. Der einfachste Weg, ein aufrufbares Objekt zu generieren, ist die Verwendung von make_scorer. Der Weg. Diese Funktion wandelt die Metrik in ein aufrufbares Objekt um, das zur Modellbewertung verwendet werden kann.

Ein typischer Anwendungsfall besteht darin, eine vorhandene Metrikfunktion aus einer Bibliothek mit einem nicht standardmäßigen Wert für einen Parameter zu umbrechen, z. B. den Beta-Parameter der Funktion fbeta_score.

>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]}, scoring=ftwo_scorer)

Der zweite Anwendungsfall besteht darin, aus einer einfachen Python-Funktion mit make_scorer ein vollständig benutzerdefiniertes Scorer-Objekt zu erstellen, das einige Parameter annehmen kann:

Im folgenden Beispiel wird ein benutzerdefinierter Scorer erstellt und der Parameter "Greater_is_better" verwendet.

>>> import numpy as np
>>> def my_custom_loss_func(ground_truth, predictions):
...     diff = np.abs(ground_truth - predictions).max()
...     return np.log(1 + diff)
...
>>> # loss_func ist mein_custom_loss_Deaktiviert den Rückgabewert von func.
>>> #Das ist der Boden_np wenn es einen Wert der Wahrheit und die unten definierte Vorhersage gibt.log(2)、0.Es wird 693 sein.
>>> loss  = make_scorer(my_custom_loss_func, greater_is_better=False)
>>> score = make_scorer(my_custom_loss_func, greater_is_better=True)
>>> ground_truth = [[1, 1]]
>>> predictions  = [0, 1]
>>> from sklearn.dummy import DummyClassifier
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf = clf.fit(ground_truth, predictions)
>>> loss(clf,ground_truth, predictions) 
-0.69...
>>> score(clf,ground_truth, predictions) 
0.69...

3.3.1.3. Implementierung des ursprünglichen Bewertungsobjekts

Sie können einen flexibleren Modellscorer generieren, indem Sie Ihr eigenes Scoring-Objekt von Grund auf neu erstellen, ohne die Factory make_scorer zu verwenden. Damit ein aufrufbares Objekt ein Scorer sein kann, muss es das in den folgenden beiden Regeln angegebene Protokoll erfüllen.

3.3.2 Klassifizierungsmetrik

sklearn.metrics Das Modul implementiert mehrere Verlust-, Score- und Dienstprogrammfunktionen, um die Klassifizierungsleistung zu messen Machen. Einige Metriken erfordern möglicherweise eine probabilistische Schätzung der positiven Klasse, der Konfidenzwerte oder der binären Bestimmungswerte. In den meisten Implementierungen kann der Parameter "sample_weight" verwendet werden, damit jede Stichprobe einen gewichteten Beitrag zur Gesamtbewertung leisten kann.

Diese sind auf die binäre Klassifizierung beschränkt:
matthews_corrcoef(y_true、y_pred [、...]) Korrelationskoeffizient der binären Klasse Matthews(MCC)
precision_recall_curve(y_true、probas_pred) Anpassungsrate gegen verschiedene Wahrscheinlichkeitsschwellen-Rückrufpaare berechnen
roc_curve(y_true、y_score [、pos_label、...]) Betriebseigenschaften des Empfängers(ROC)

Diese funktionieren auch in mehreren Klassen:
cohen_kappa_score(y1、y2 [、labels、weights]) Cohen's kappa: Statistiken, die Vereinbarungen zwischen Annotatoren messen.
confusion_matrix(y_true、y_pred [、labels、...]) Berechnen Sie eine Verwirrungsmatrix, um die Genauigkeit der Klassifizierung zu bewerten
hinge_loss(y_true、pred_decision [、labels、...]) Durchschnittlicher Scharnierverlust(Denormalisiert)

Diese funktionieren auch für Multi-Labels:
accuracy_score(y_true、y_pred [、normalize、...]) Genauigkeitsklassifizierungsbewertung.
classification_report(y_true、y_pred [、...]) Erstellen Sie einen Textbericht mit den wichtigsten Klassifizierungsmetriken
f1_score(y_true、y_pred [、labels、...]) Berechnen Sie die F1-Punktzahl. Dies wird auch als ausgeglichene F-Partitur oder F-Dur bezeichnet
fbeta_score(y_true、y_pred、beta [、labels、...]) Berechnen Sie den F Beta Score
hamming_loss(y_true、y_pred [、labels、...]) Berechnen Sie den durchschnittlichen Brummverlust.
jaccard_similarity_score(y_true、y_pred [、...]) Jaccard Ähnlichkeitsbewertung
log_loss(y_true、y_pred [、eps、normalize、...]) Protokollverlust, auch als logistischer Verlust oder Kreuzentropieverlust bezeichnet.
precision_recall_fscore_support(y_true、y_pred) Konformitätsrate, Rückrufrate, F jeder Klasse-Maßnahme und Unterstützung berechnen
precision_score(y_true、y_pred [、labels、...]) Berechnen Sie die Genauigkeit
recall_score(y_true、y_pred [、labels、...]) Rückruf berechnen
zero_one_loss(y_true、y_pred [、normalize、...]) Kein Klassifizierungsverlust.

Diese funktionieren mit Binär- und Multi-Label (nicht Multi-Class)
average_precision_score(y_true、y_score [、...]) Durchschnittliche Genauigkeit aus der vorhergesagten Punktzahl(AP)
roc_auc_score(y_true、y_score [、average、...]) Fläche unter der Kurve aus der vorhergesagten Punktzahl(AUC)

In den folgenden Unterabschnitten werden diese Funktionen beschrieben und einige Hinweise zu allgemeinen API- und Metrikdefinitionen vorangestellt.

3.3.2.1. Von binär zu Multi-Class und Multi-Label

Grundsätzlich sind einige Metriken für die binäre Klassifizierungsaufgabe definiert (f1_score. metrics.f1_score), roc_auc_score. In solchen Fällen werden standardmäßig nur positive Beschriftungen ausgewertet und die positive Klasse mit 1 beschriftet (obwohl sie mit dem Parameter pos_label konfiguriert werden kann). Wenn eine binäre Metrik auf ein Problem mit mehreren Klassen oder mehreren Bezeichnungen erweitert wird, werden die Daten als Sammlung von binären Problemen behandelt (eines pro Klasse). Es gibt verschiedene Möglichkeiten, binäre Metrikberechnungen über eine Reihe von Klassen zu mitteln, was in einigen Szenarien hilfreich ist. Wenn möglich, sollten Sie mit dem Parameter "Durchschnitt" zwischen diesen wählen.

--"Makro"berechnet den Durchschnitt der binären Metriken und gibt jeder Klasse gleiche Gewichte. Bei Problemen, bei denen seltene Klassen wichtig sind, kann die Makro-Mittelung eine Möglichkeit sein, die Leistung zu betonen. Andererseits ist die Annahme, dass alle Klassen gleich wichtig sind, oft nicht wahr, so dass die Makro-Mittelung die schlechte Leistung in seltenen Klassen im Allgemeinen überbetont. --"gewichtet"Klassenungleichgewichte werden" gewichtet ", indem der Durchschnitt der binären Metriken berechnet wird, die durch das Vorhandensein der Punktzahl jeder Klasse in einer echten Datenstichprobe gewichtet werden. -"Mikro"trägt gleichermaßen zur Gesamtmetrik für jedes Probenklassenpaar bei (mit Ausnahme der Ergebnisse des Probengewichts). Anstatt die Metriken nach Klassen zu summieren, summieren Sie die Dividenden und Teiler, aus denen die Metriken bestehen, nach Klassen, um den Gesamtquotienten zu berechnen. Die Mikromittelung kann in Einstellungen mit mehreren Beschriftungen Vorrang haben, einschließlich der Klassifizierung mehrerer Klassen, bei der viele Klassen ignoriert werden. -"samples"gilt nur für Multi-Label-Probleme. Stattdessen berechnet es die wahren und vorhergesagten Klassenmetriken für jede Stichprobe von Bewertungsdaten und gibt ihren (sample_weight - gewichteten) Durchschnitt zurück.

Daten mit mehreren Klassen werden als Array von Klassenbeschriftungen metrisch wie ein binäres Ziel bereitgestellt, während Daten mit mehreren Beschriftungen die Zelle "[i, j" sind, wenn Probe "i" die Bezeichnung "j" hat. ] `Gibt andernfalls den Wert 1 zurück.

3.3.2.2. Genauigkeitsbewertung

Genauigkeitsbewertung Die Funktion ist ein genauer Vorhersageprozentsatz (Standard) oder eine Zählung ("normalisieren") = False`) wird berechnet. Bei der Klassifizierung mit mehreren Etiketten gibt diese Funktion eine Teilmenge der Genauigkeit zurück. Wenn der gesamte Satz vorhergesagter Beschriftungen in der Stichprobe genau mit dem tatsächlichen Satz von Beschriftungen übereinstimmt, beträgt die Genauigkeit der Teilmenge 1,0. Ansonsten ist es 0.0.

\texttt{accuracy}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} 1(\hat{y}_i = y_i)

Wobei $ 1 (x) $ die Indikatorfunktion ist (https://en.wikipedia.org/wiki/Indicator_function).

>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
>>> accuracy_score(y_true, y_pred, normalize=False)
2

Für Mehrfachetiketten mit binärer Etikettenanzeige:

>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5

--Beispiel:

3.3.2.3. Kappa-Koeffizient

Die Funktion cohen_kappa_score ist der [Kappa-Koeffizient](https: //en.wikipedia. org / wiki / Cohen% 27s_kappa) wird berechnet. Diese Skala soll die Kennzeichnung durch verschiedene menschliche Kommentatoren vergleichen. Der κ-Wert (siehe Dokument) ist eine Zahl zwischen -1 und 1. Werte über 8 gelten im Allgemeinen als gute Übereinstimmungen. Unter Null bedeutet keine Übereinstimmung (praktisch zufälliges Etikett). Der κ-Score kann für binäre Probleme oder Probleme mit mehreren Klassen berechnet werden, jedoch nicht für Probleme mit mehreren Labels (es sei denn, Sie berechnen den Score für jedes Label manuell) und für zwei oder mehr Anmerkungen.

>>> from sklearn.metrics import cohen_kappa_score
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> cohen_kappa_score(y_true, y_pred)
0.4285714285714286

3.3.2.4. Verwirrungsmatrix

confusion_matrix Die Funktion ist [Confusion Matrix](https: //en.wikipedia. Bewerten Sie die Klassifizierungsgenauigkeit durch Berechnung (org / wiki / Confusion_matrix). Per Definition ist der Verwirrungsmatrixeintrag $ i, j $ die tatsächliche Anzahl von Beobachtungen für die Gruppe $ i $, wird jedoch voraussichtlich zur Gruppe $ j $ gehören. Hier ist ein Beispiel:

>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

Eine visuelle Darstellung einer solchen Verwirrungsmatrix (diese Abbildung ist die Verwirrungsmatrix) (http://scikit-learn.org/0.18/auto_examples/model_selection/plot_confusion_matrix.html#sphx-glr-auto-examples- Ein Beispiel für Modellauswahl-Plot-Verwirrung-Matrix-py)).

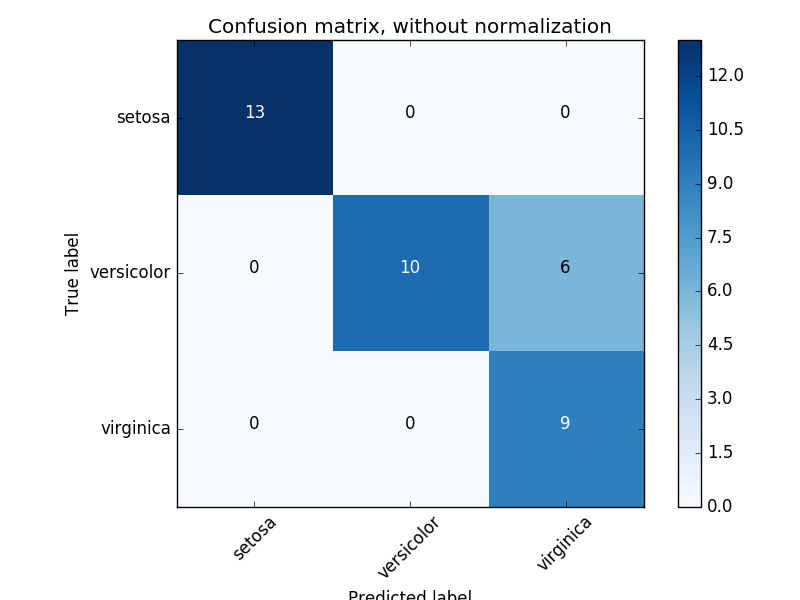
Bei binären Problemen können Sie wie folgt echte negative, falsche positive, falsche negative und echte positive Zählungen erhalten:

--Beispiel:

3.3.2.5 Klassifizierungsbericht

Die Funktion Klassifizierungsbericht erstellt einen Textbericht mit den wichtigsten Klassifizierungsmetriken. Das Folgende ist ein kleines Beispiel für einen benutzerdefinierten "Zielnamen" und eine geschätzte Bezeichnung.

>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
             precision    recall  f1-score   support

    class 0       0.67      1.00      0.80         2
    class 1       0.00      0.00      0.00         1
    class 2       1.00      0.50      0.67         2

avg / total       0.67      0.60      0.59         5

--Beispiel:

3.3.2.6. Brummverlust

hamming_loss berechnet den durchschnittlichen Brummverlust oder den Brummabstand zwischen zwei Probensätzen Machen. Wenn $ \ hat {y} j $ der vorhergesagte Wert des $ j $ -ten Labels der gegebenen Stichprobe ist, dann ist $ y_j $ der entsprechende wahre Wert und $ n \ text {label} $ ist die Klasse oder Die Anzahl der Labels, der Brummverlust $ L_ {Hamming} $, ist wie folgt definiert.

L_{Hamming}(y, \hat{y}) = \frac{1}{n_\text{labels}} \sum_{j=0}^{n_\text{labels} - 1} 1(\hat{y}_j \not= y_j)

Wobei $ 1 (x) $ die Indikatorfunktion ist (https://en.wikipedia.org/wiki/Indicator_function).

>>> from sklearn.metrics import hamming_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> hamming_loss(y_true, y_pred)
0.25

Für Mehrfachetiketten mit binärer Etikettenanzeige:

>>>
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2)))
0.75

** (Hinweis) ** In der Mehrklassenklassifizierung beträgt der Brummverlust [Zero One Loss](# 33213-% E3% 82% BC% E3% 83% AD1% E3% 81% A4% E3% 81% AE% E6 % 90% 8D% E5% A4% B1) Entspricht dem der Funktion ähnlichen Brummabstand zwischen "y_true" und "y_pred". Eins-zu-eins-Verluste bestrafen jedoch Vorhersagesätze, die nicht genau mit dem tatsächlichen Satz übereinstimmen, während Brummverluste einzelne Etiketten benachteiligen. Daher liegt der durch den Verlust von Null 1 begrenzte Brummverlust immer zwischen 0 und 1, und die Vorhersage der richtigen Teilmenge oder Obermenge des wahren Etiketts summt zwischen Null und 1. Der Verlust wird beseitigt.

3.3.2.7 Jacquard-Ähnlichkeitskoeffizienten-Score

jaccard_similarity_score Die Funktion wird auch als Jaccard-Index zwischen gepaarten Labelsätzen bezeichnet. Berechnet den Durchschnitt (Standard) oder die Gesamtzahl der Geschlechtsfaktoren (https://en.wikipedia.org/wiki/Jaccard_index). Der Jaccard-Ähnlichkeitskoeffizient für die $ i $ -te Stichprobe mit dem Messwert-Label-Set $ y_i $ und dem vorhergesagten Label-Set $ \ hat {y} _i $ ist wie folgt definiert:

J(y_i, \hat{y}_i) = \frac{|y_i \cap \hat{y}_i|}{|y_i \cup \hat{y}_i|}.

Für die Binär- und Mehrklassenklassifizierung entspricht der Jaccard-Ähnlichkeitskoeffizientenwert der Klassifizierungsgenauigkeit.

>>> import numpy as np
>>> from sklearn.metrics import jaccard_similarity_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> jaccard_similarity_score(y_true, y_pred)
0.5
>>> jaccard_similarity_score(y_true, y_pred, normalize=False)
2

Für Mehrfachetiketten mit binärer Etikettenanzeige:

>>>
>>> jaccard_similarity_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.75

3.3.2.8 Konformitätsrate, Rückrufrate, F-Wert (F-Maß)

Intuitiv ist Fitness die Fähigkeit des Klassifikators, zu verhindern, dass negative Proben als positiv gekennzeichnet werden. Rate](https://en.wikipedia.org/wiki/Precision_and_recall#Recall) ist die Fähigkeit des Klassifikators, alle positiven Proben zu finden. Die F-Werte ($ F_β $ - und $ F \ 1 $ -Messungen) können als gewichtete harmonisierte Mittelwerte für Präzision und Rückruf interpretiert werden. Wenn $ \ beta = 1 $, sind $ F \ beta $ und $ F \ _1 $ gleichwertig, und Rückruf und Präzision sind ebenso wichtig. precision_recall_curve ist die Präzisionsrückrufratenkurve aus dem Wahrheitsetikett. Berechnen Sie die vom Klassifikator angegebene Punktzahl, indem Sie den Schwellenwert ändern. aver_precision_score Die Funktion berechnet die durchschnittliche Genauigkeit (AP) aus der vorhergesagten Punktzahl. .. Diese Bewertung entspricht dem Bereich unter der Präzisionsrückrufratenkurve. Der Wert liegt zwischen 0 und 1, je höher desto besser. Bei der zufälligen Vorhersage ist AP der Prozentsatz der positiven Proben.

Verschiedene Funktionen können verwendet werden, um die Genauigkeits-, Rückruf- und F-Wert-Bewertungen zu analysieren.
average_precision_score(y_true,y_score [,...]) Durchschnittliche Präzisionsrate aus der vorhergesagten Punktzahl(AP)Berechnen
f1_score(y_true,y_pred [,labels,...]) Berechnen Sie die F1-Punktzahl. Dies wird auch als ausgeglichene F-Partitur oder F-Dur bezeichnet
fbeta_score(y_true,y_pred,beta [,labels,...]) Berechnen Sie den F Beta Score
precision_recall_curve(y_true,probas_pred) Anpassungsrate gegen verschiedene Wahrscheinlichkeitsschwellen-Rückrufpaare berechnen
precision_recall_fscore_support(y_true,y_pred) Konformitätsrate jeder Klasse,Erinnern,F-Maßnahme und Unterstützung berechnen
precision_score(y_true,y_pred [,labels,...]) Berechnen Sie die Genauigkeit
recall_score(y_true,y_pred [,labels,...]) Rückruf berechnen

präzise_recall_curve Beachten Sie, dass die Funktion auf binär beschränkt ist. .. Die Funktion aver_precision_score funktioniert nur in binärer Klassifizierung und im Multi-Label-Indikatorformat.

--Beispiel:
average_precision_score(y_true,y_score [,...]) Durchschnittliche Genauigkeit aus der vorhergesagten Punktzahl(AP)Berechnen
f1_score(y_true,y_pred [,labels,...]) Berechnen Sie die F1-Punktzahl. Dies wird auch als ausgeglichene F-Partitur oder F-Dur bezeichnet
fbeta_score(y_true,y_pred,beta [,labels,...]) Berechnen Sie den F Beta Score
precision_recall_curve(y_true,probas_pred) Anpassungsrate an Schwellenwerte verschiedener Wahrscheinlichkeiten-Rückrufpaare berechnen
precision_recall_fscore_support(y_true,y_pred) Konformitätsrate jeder Klasse,Erinnern,Berechnen Sie den F-Wert und die Unterstützung
precision_score(y_true,y_pred [,labels,...]) Berechnen Sie die Genauigkeit
recall_score(y_true,y_pred [,labels,...]) Rückruf berechnen
precision_recall_Beachten Sie, dass die Kurvenfunktion auf den binären Fall beschränkt ist. average_precision_Score-Funktion,Funktioniert nur in binärer Klassifizierung und im Multi-Label-Indikatorformat.

Beachten Sie, dass die Funktion priority_recall_curve auf binäre Fälle beschränkt ist. Die Funktion aver_precision_score funktioniert nur in binärer Klassifizierung und im Multi-Label-Indikatorformat. Beispiel: Ein Beispiel für die Verwendung von f1_score zum Klassifizieren von Textdokumenten finden Sie unter Klassifizieren von Textdokumenten mithilfe von Sparse-Funktionen. Ein Beispiel für die Verwendung von Precision_score und Recall_score zum Schätzen von Parametern mithilfe der Rastersuche bei der verschachtelten gegenseitigen Validierung finden Sie unter Parameterschätzung mithilfe der Rastersuche mit Kreuzvalidierung. Unter Precision-Recall finden Sie ein Beispiel für die Verwendung von priority_recall_curve zur Bewertung der Ausgabequalität eines Klassifikators. Ein Beispiel für die Verwendung von precision_recall_curve zum Auswählen von Features in einem spärlichen linearen Modell finden Sie unter Sparse Recovery für spärliche lineare Modelle: Feature-Auswahl.

3.3.2.8.1. Binäre Klassifizierung

In der binären Klassifizierungsaufgabe geben die Begriffe "positiv" und "negativ" die Vorhersagen des Klassifizierers an, und die Begriffe "wahr" und "falsch" geben "Beobachtung" an, ob die Vorhersagen externen Urteilen entsprechen. Auch genannt). Mit diesen Definitionen können Sie die folgende Tabelle erstellen.

Tatsächliche Klasse (Beobachtung)
Vorhersageklasse (erwarteter Wert) tp (wahres positives) korrektes Ergebnis fp (falsch positiv) Unerwartetes Ergebnis
fn (falsch negativ) fehlendes Ergebnis tn (wahres negatives) Ergebnis ist falsch

In diesem Zusammenhang können Sie die Konzepte Präzision, Rückruf und F-Wert definieren.

\text{precision} = \frac{tp}{tp + fp}, \\
\text{recall} = \frac{tp}{tp + fn}, \\
F_\beta = (1 + \beta^2) \frac{\text{precision} \times \text{recall}}{\beta^2 \text{precision} + \text{recall}}.

Hier sind einige kleine Beispiele für die binäre Klassifizierung:

>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)  
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=0.5)  
0.83...
>>> metrics.fbeta_score(y_true, y_pred, beta=1)  
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=2) 
0.55...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5)  
(array([ 0.66...,  1.        ]), array([ 1. ,  0.5]), array([ 0.71...,  0.83...]), array([2, 2]...))


>>> import numpy as np
>>> from sklearn.metrics import precision_recall_curve
>>> from sklearn.metrics import average_precision_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> precision, recall, threshold = precision_recall_curve(y_true, y_scores)
>>> precision  
array([ 0.66...,  0.5       ,  1.        ,  1.        ])
>>> recall
array([ 1. ,  0.5,  0.5,  0. ])
>>> threshold
array([ 0.35,  0.4 ,  0.8 ])
>>> average_precision_score(y_true, y_scores)  
0.79...

3.3.2.8.2. Klassifizierung von Mehrfachklassen und Mehrfachetiketten

Mit Aufgaben zur Klassifizierung mehrerer Klassen und Etiketten können Sie die Konzepte der Präzision, des Rückrufs und des F-Werts auf jedes Etikett einzeln anwenden. Wie oben, aver_precision_score (nur Multilabel), [f1_score](http: / /scikit-learn.org/0.18/modules/generated/sklearn.metrics.f1_score.html#sklearn.metrics.f1_score), [fbeta_score](http://scikit-learn.org/0.18/modules/generated/sklearn. metrics.fbeta_score.html # sklearn.metrics.fbeta_score), [präzise_recall_fscore_support](http://scikit-learn.org/0.18/modules/generated/sklearn.metrics.precision_recall_fscore_support.html#sklearn_scort_score ](Http://scikit-learn.org/0.18/modules/generated/sklearn.metrics.precision_score.html#sklearn.metrics.precision_score) und [Recall_score](http://scikit-learn.org/0.18/ modules / generiert / sklearn.metrics.recall_score.html # sklearn.metrics.recall_score) Es gibt verschiedene Möglichkeiten, Ergebnisse zwischen den durch das Argument "Durchschnitt" der Funktion angegebenen Beschriftungen zu kombinieren. Die "Mikro" -Mittelung in einer Mehrklasseneinstellung, die alle Beschriftungen enthält, führt zu gleichen Anpassungs-, Rückruf- und F-Werten, aber die "gewichtete" Mittelung liegt nicht zwischen Anpassung und Rückruf. Beachten Sie, dass ein F-Score generiert wird.

Um dies deutlicher zu machen, betrachten Sie die folgende Notation:

Dann wird die Metrik definiert als:

average Precision Recall F_beta
"micro" $P(y, \hat{y})$ $R(y, \hat{y})$ $F_\beta(y, \hat{y})$
"samples" $\frac{1}{\left|S\right|} \sum_{s \in S} P(y_s, \hat{y}_s)$ $\frac{1}{\left|S\right|} \sum_{s \in S} R(y_s, \hat{y}_s)$ $\frac{1}{\left|S\right|} \sum_{s \in S} F_\beta(y_s, \hat{y}_s)$
"macro" $\frac{1}{\left|L\right|} \sum_{l \in L} P(y_l, \hat{y}_l)$ $\frac{1}{\left|L\right|} \sum_{l \in L} R(y_l, \hat{y}_l)$ $\frac{1}{\left|L\right|} \sum_{l \in L} F_\beta(y_l, \hat{y}_l)$
"weighted" $\frac{1}{\sum_{l \in L} \left|\hat{y}_l\right|} \sum_{l \in L} \left|\hat{y}_l\right| P(y_l, \hat{y}_l)$ $\frac{1}{\sum_{l \in L} \left|\hat{y}_l\right|} \sum_{l \in L} \left|\hat{y}_l\right| R(y_l, \hat{y}_l)$ $\frac{1}{\sum_{l \in L} \left|\hat{y}_l\right|} \sum_{l \in L} \left|\hat{y}_l\right| F_\beta(y_l, \hat{y}_l)$
None $\langle P(y_l, \hat{y}_l) | l \in L \rangle$ $\langle R(y_l, \hat{y}_l) | l \in L \rangle$ $\langle F_\beta(y_l, \hat{y}_l) | l \in L \rangle$ 
>>> from sklearn import metrics
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> metrics.precision_score(y_true, y_pred, average='macro')  
0.22...
>>> metrics.recall_score(y_true, y_pred, average='micro')
... 
0.33...
>>> metrics.f1_score(y_true, y_pred, average='weighted')  
0.26...
>>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5)  
0.23...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None)
... 
(array([ 0.66...,  0.        ,  0.        ]), array([ 1.,  0.,  0.]), array([ 0.71...,  0.        ,  0.        ]), array([2, 2, 2]...))

Einige Bezeichnungen können in Klassifizierungen mit mehreren Klassen ausgeschlossen werden, die "negative Klassen" enthalten.

>>>
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro')
... # excluding 0, no labels were correctly recalled
0.0

In ähnlicher Weise können Beschriftungen, die in der Datenprobe nicht vorhanden sind, in der Makro-Mittelung erklärt werden.

>>>
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro')
... 
0.166...

3.3.2.9 Scharnierverlust

hing_loss Die Funktion ist eine einseitige Metrik, die nur Vorhersagefehler berücksichtigt [Gelenkverlust] ](Https://en.wikipedia.org/wiki/Hinge_loss) wird verwendet, um den durchschnittlichen Abstand zwischen dem Modell und den Daten zu berechnen. (Der Hinging-Verlust wird in Klassifizierern für maximale Margen wie Support-Vektor-Maschinen verwendet.) Wenn das Etikett mit +1 und -1 codiert ist, ist $ y: $ der wahre Wert, $ w $ ist die vorhergesagte Entscheidung als Ausgabe von entscheidungsfunktion und der Scharnierverlust ist wie folgt: Es ist definiert.

L_\text{Hinge}(y, w) = \max\left\{1 - wy, 0\right\} = \left|1 - wy\right|_+

Wenn es mehr als ein Label gibt, verwendet hinte_loss eine Mehrklassenvariante für Crammer & Singer. Hier ist ein Artikel, der es beschreibt. Multiklasse, wenn $ y_w $ die vorhergesagte Entscheidung des wahren Labels ist und $ y_t $ die maximale vorhergesagte Entscheidung aller anderen Labels ist, für die die von der Entscheidungsfunktion vorhergesagte Entscheidung ausgegeben wird. Scharnierverlust

L_\text{Hinge}(y_w, y_t) = \max\left\{1 + y_t - y_w, 0\right\}

Hier ist ein kleines Beispiel, das zeigt, wie die Funktion hidden_loss mit dem svm-Klassifikator für Probleme mit binären Klassen verwendet wird.

>>> from sklearn import svm
>>> from sklearn.metrics import hinge_loss
>>> X = [[0], [1]]
>>> y = [-1, 1]
>>> est = svm.LinearSVC(random_state=0)
>>> est.fit(X, y)
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
     intercept_scaling=1, loss='squared_hinge', max_iter=1000,
     multi_class='ovr', penalty='l2', random_state=0, tol=0.0001,
     verbose=0)
>>> pred_decision = est.decision_function([[-2], [3], [0.5]])
>>> pred_decision  
array([-2.18...,  2.36...,  0.09...])
>>> hinge_loss([-1, 1, 1], pred_decision)  
0.3...

Hier ist ein Beispiel für die Verwendung der Funktion hige_loss mit dem SVM-Klassifizierer für Probleme mit mehreren Klassen:

>>>
>>> X = np.array([[0], [1], [2], [3]])
>>> Y = np.array([0, 1, 2, 3])
>>> labels = np.array([0, 1, 2, 3])
>>> est = svm.LinearSVC()
>>> est.fit(X, Y)
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
     intercept_scaling=1, loss='squared_hinge', max_iter=1000,
     multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
     verbose=0)
>>> pred_decision = est.decision_function([[-1], [2], [3]])
>>> y_true = [0, 2, 3]
>>> hinge_loss(y_true, pred_decision, labels)  
0.56...

3.3.2.10 Protokollverlust

Der logarithmische Verlust, auch als logistischer Regressionsverlust oder Kreuzentropieverlust bekannt, wird durch Wahrscheinlichkeitsschätzung definiert. Es wird häufig in (polygonalen) logistischen Regressions- und neuronalen Netzen sowie in einigen Varianten der prädiktiven Maximierung verwendet und wird verwendet, um die probabilistische Ausgabe des Klassifikators (pred_proba) anstelle einer diskreten Vorhersage zu bewerten. tun können.

Bei binären Klassifikationen mit der wahren Bezeichnung $ y \ in \ {0,1 } $ und der Wahrscheinlichkeitsschätzung $ p = \ operatorname {Pr} (y = 1) $ ist der Protokollverlust pro Stichprobe die wahre Bezeichnung Negative Log-Wahrscheinlichkeit eines bestimmten Klassifikators.

L_{\log}(y, p) = -\log \operatorname{Pr}(y|p) = -(y \log (p) + (1 - y) \log (1 - p))

Dies erstreckt sich wie folgt auf den Fall der Mehrfachklasse. Codieren Sie die wahre Bezeichnung für den Probensatz als eine der K-Binärindikatormatrix $ Y $. Das heißt, wenn Probe i eine Beschriftung k hat, die aus einer Menge von K Beschriftungen entnommen wurde, dann ist $ y_ {i, k} = 1 $. Sei $ P $ die Matrix für die Wahrscheinlichkeitsschätzung und sei $ p_ {i, k} = \ operatorname {Pr} (t_ {i, k} = 1) $. Dann ist der logarithmische Verlust des gesamten Satzes

L_{\log}(Y, P) = -\log \operatorname{Pr}(Y|P) = - \frac{1}{N} \sum_{i=0}^{N-1} \sum_{k=0}^{K-1} y_{i,k} \log p_{i,k}

Wenn dies binär ist, ist $ p_ {i, 0} = 1 --p_ {i, 1} $ und $ y_ {i, 0} = 1 --y_ {i, 1} $. Daher ist die interne Summe $ y_ {i, Größer als k} \ in \ {0,1 } $ führt zu einem Verlust des binären Protokolls.

log_loss Die Funktion wird jetzt von der Schätzmethode "Predict_proba" zurückgegeben. Berechnet den Log-Verlust anhand eines Ground-Truth-Labels und einer Liste von Wahrscheinlichkeitsmatrizen.

>>> from sklearn.metrics import log_loss
>>> y_true = [0, 0, 1, 1]
>>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
>>> log_loss(y_true, y_pred)    
0.1738...

Das erste "[.9, .1]" von "y_pred" zeigt an, dass die erste Probe eine 90% ige Chance hat, das Label 0 zu haben. Der Protokollverlust ist nicht negativ.

3.3.2.11 Matthews-Korrelationskoeffizient

matthews_corrcoef Die Funktion ist eine binäre Klasse [Matthew Correlation Coefficient (MCC)]( (https://en.wikipedia.org/wiki/Matthews_correlation_coefficient) wird berechnet. Wikipedia zitieren:

Matthews Korrelationskoeffizienten werden beim maschinellen Lernen als Maß für die Qualität der binären (Zwei-Klassen-) Klassifizierung verwendet. In Anbetracht der positiven und negativen positiven und negativen Ergebnisse wird es im Allgemeinen als ausgewogenes Maß angesehen, das auch in sehr unterschiedlichen Klassengrößen verwendet werden kann. MCC ist im Wesentlichen ein Korrelationskoeffizientenwert zwischen -1 und +1. Ein Koeffizient von +1 repräsentiert eine vollständige Vorhersage, 0 repräsentiert eine durchschnittliche zufällige Vorhersage und -1 repräsentiert eine inverse Vorhersage. Statistiken werden auch als φ-Koeffizient bezeichnet.

Wenn $ tp $, $ tn $, $ fp $ und $ fn $ wahr positive, wahr negative, falsch positive bzw. falsch negative Zahlen sind, ist der MCC-Koeffizient

MCC = \frac{tp \times tn - fp \times fn}{\sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.

Das folgende Beispiel zeigt, wie die Funktion matthews_corrcoef verwendet wird.

>>>
>>> sklearn.Import aus Metriken Matthews_corrcoef
>>> y_true = [+1、+1、+1、-1]
>>> y_pred = [+1、-1、+1、+1]
>>> matthews_corrcoef（y_true、y_pred）
-0.33 ...

3.3.2.12. Betriebseigenschaften des Empfängers (ROC)

Die Funktion roc_curve ist die [Empfängerverhaltenskennlinie oder ROC-Kurve](https :: //en.wikipedia.org/wiki/Receiver_operating_characteristic) wird berechnet. Wikipedia zitieren:

Die Empfänger-Betriebseigenschaften (ROC) oder einfach die ROC-Kurve sind grafische Darstellungen, die die Leistung des binären Klassifizierungssystems bei Änderung der Unterscheidungsschwelle zeigen. Es wird erstellt, indem der Prozentsatz der echten Positiven aus den Positiven (TPR = wahre positive Rate) gegen den Prozentsatz der falschen Positiven aus den Negativen (FPR = falsche positive Rate) bei verschiedenen Schwellenwerteinstellungen aufgetragen wird. TPR wird auch als Suszeptibilität bezeichnet, und FPR ist die Spezifität oder die wahre negative Rate minus eins.

Diese Funktion erfordert einen echten Binärwert und eine Zielpunktzahl. Dies ist entweder eine positive Klassenwahrscheinlichkeitsschätzung, ein Konfidenzwert oder eine binäre Entscheidung. Das Folgende ist ein kleines Beispiel für die Verwendung der Funktion roc_curve.

>>> import numpy as np
>>> from sklearn.metrics import roc_curve
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)
>>> fpr
array([ 0. ,  0.5,  0.5,  1. ])
>>> tpr
array([ 0.5,  0.5,  1. ,  1. ])
>>> thresholds
array([ 0.8 ,  0.4 ,  0.35,  0.1 ])

Diese Abbildung zeigt ein Beispiel für eine solche ROC-Kurve.

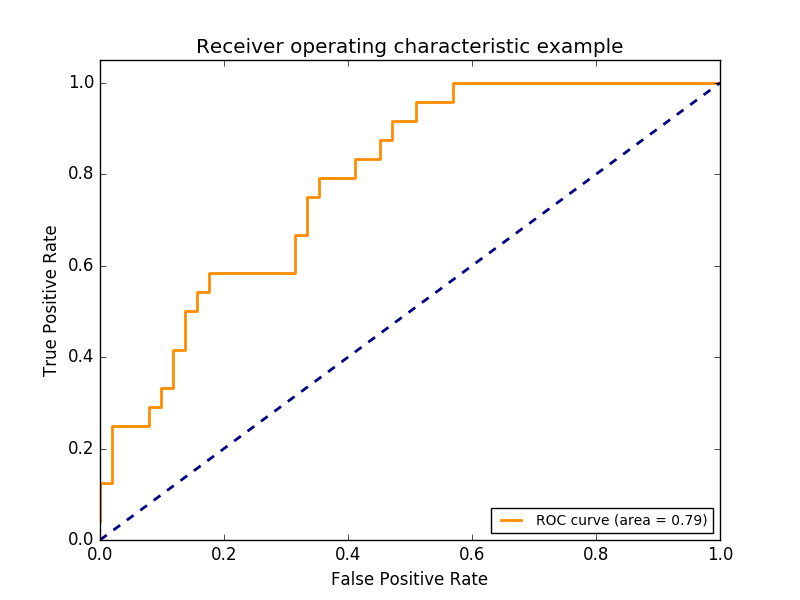
roc_auc_score Die Funktion ist die Empfängerbetriebseigenschaft (ROC), die durch AUC oder AUROC dargestellt wird. ) Berechnen Sie die Fläche unter der Kurve. Durch Berechnung der Fläche unter der ROC-Kurve werden die Kurveninformationen zu einer Zahl zusammengefasst. Weitere Informationen finden Sie im Wikipedia-Artikel über AUC (https://en.wikipedia.org/wiki/Receiver_operating_characteristic#Area_under_the_curve).

>>> import numpy as np
>>> from sklearn.metrics import roc_auc_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> roc_auc_score(y_true, y_scores)
0.75

Bei der Klassifizierung mit mehreren Etiketten wird die Funktion roc_auc_score erweitert, indem die Etiketten wie oben beschrieben gemittelt werden. Für ROC ist es nicht erforderlich, den Schwellenwert für jedes Etikett im Vergleich zu Metriken wie Teilmengengenauigkeit, Brummverlust und F1-Punktzahl zu optimieren. Die Funktion roc_auc_score kann auch bei der Klassifizierung mehrerer Klassen verwendet werden, wenn die vorhergesagte Ausgabe binär weiterentwickelt wurde.

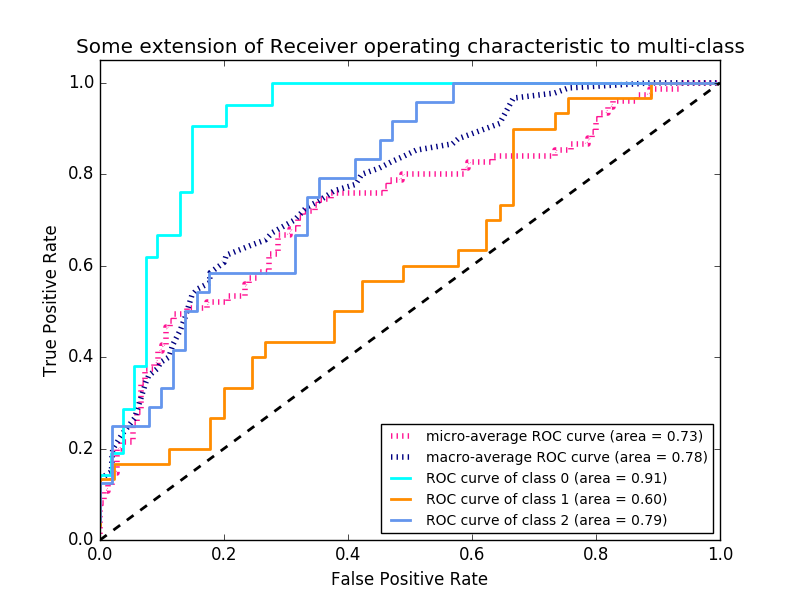
--Beispiel:

3.3.2.13. 0-1 Verlust

zero_one_loss Die Funktion ist 0- für $ n_ {\ text {samples}} $ 1 Berechnen Sie die Summe oder den Durchschnitt des Klassifizierungsverlusts $ (L_ {0-1}) $. Standardmäßig ist die Funktion auf die Probe normalisiert. Um die Summe von $ L_ {0-1} $ zu ermitteln, setzen Sie "normalize" auf "False". Bei der Klassifizierung mit mehreren Labels bewertet zero_one_loss die Teilmenge mit 1, wenn das Label genau mit der Vorhersage übereinstimmt, und mit Null, wenn ein Fehler vorliegt. Standardmäßig gibt diese Funktion den Prozentsatz einer unvollständig vorhergesagten Teilmenge zurück. Um stattdessen die Anzahl solcher Teilmengen zu erhalten, setzen Sie "normalize" auf "False" Wenn $ \ hat {y} i $ der vorhergesagte Wert für die $ i $ -te Stichprobe ist und $ y_i $ der entsprechende wahre Wert ist, dann ist der 0-1-Verlust $ L {0-1} $ Ist definiert in.

L_{0-1}(y_i, \hat{y}_i) = 1(\hat{y}_i \not= y_i)

Wobei $ 1 (x) $ die Indikatorfunktion ist (https://en.wikipedia.org/wiki/Indicator_function).

>>> from sklearn.metrics import zero_one_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> zero_one_loss(y_true, y_pred)
0.25
>>> zero_one_loss(y_true, y_pred, normalize=False)
1

Bei Mehrfachetiketten mit einem binären Etikettenindikator liegt ein Fehler im ersten Etikettensatz [0,1] vor.

>>>
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5

>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)),  normalize=False)
1

--Beispiel:

3.3.2.14 Brier Score Verlust

brier_score_loss Die Funktion ist die Binärklasse [Brier Score](https: // en). .wikipedia.org / wiki / Brier_score) wird berechnet. Wikipedia zitieren:

Der Brier-Score ist eine gute Bewertungsfunktion, die die Genauigkeit probabilistischer Vorhersagen misst. Es kann auf Aufgaben angewendet werden, bei denen Vorhersagen einer Reihe sich gegenseitig ausschließender diskreter Ergebnisse Wahrscheinlichkeiten zuweisen müssen.

Diese Funktion gibt die Punktzahl der mittleren quadratischen Differenz zwischen dem tatsächlichen Ergebnis und der erwarteten Wahrscheinlichkeit eines möglichen Ergebnisses zurück. Das tatsächliche Ergebnis muss 1 oder 0 sein (wahr oder falsch), aber die vorhergesagte Wahrscheinlichkeit des tatsächlichen Ergebnisses liegt zwischen 0 und 1. Der Verlust der Brier-Punktzahl beträgt ebenfalls 0 zu 1, und je niedriger die Punktzahl (je kleiner die durchschnittliche quadratische Differenz) ist, desto genauer ist die Vorhersage. Dies kann als Maß für die "Entfernungsmessung" einer Reihe probabilistischer Vorhersagen angesehen werden.

BS = \frac{1}{N} \sum_{t=1}^{N}(f_t - o_t)^2

Dabei ist $ N $ die Gesamtzahl der Vorhersagen und $ f_t $ die vorhergesagte Wahrscheinlichkeit des tatsächlichen Ergebnisses $ o_t $.

Hier ist ein kleines Beispiel für die Verwendung dieser Funktion:

>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.4])
>>> y_pred = np.array([0, 1, 1, 0])
>>> brier_score_loss(y_true, y_prob)
0.055
>>> brier_score_loss(y_true, 1-y_prob, pos_label=0)
0.055
>>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham")
0.055
>>> brier_score_loss(y_true, y_prob > 0.5)
0.0

--Beispiel:

3.3.3. Multi-Label-Ranking-Metrik

Beim Multi-Label-Lernen kann jeder Probe eine beliebige Anzahl von Ground-True-Labels zugeordnet werden. Das Ziel ist es, eine hohe Punktzahl zu erzielen und den Wahrheitspreis vor Ort zu platzieren.

3.3.3.1. Abdeckungsfehler

Coverage_error Die Funktion ist endgültig, sodass alle wahren Bezeichnungen vorhergesagt werden. Berechnen Sie die durchschnittliche Anzahl von Etiketten, die in einer typischen Prognose enthalten sein müssen. Dies ist nützlich, wenn Sie wissen möchten, wie viele Top-Score-Labels Sie durchschnittlich vorhersagen müssen, ohne ihren wahren Wert zu verlieren. Daher ist der beste Wert für diese Metrik die durchschnittliche Anzahl wahrer Beschriftungen. In Anbetracht der binären Indikatormatrix für Ground-Truth-Labels und der mit jedem Label verbundenen Punktzahl ist die Abdeckung offiziell definiert als:

Offiziell sind 2 der Grundwahrheitsbezeichnungen $ y \ in \ left \\ {0, 1 \ right \} ^ {n \ _ \ text {samples} \ times n \ _ \ text {labels}} $ Angesichts der Basisindikatormatrix und der jedem Label zugeordneten Punktzahl $ \ hat {f} \ in \ mathbb {R} ^ {n \ _ \ text {samples} \ times n \ _ \ text {label}} $ , Abdeckung

coverage(y, \hat{f}) = \frac{1}{n_{\text{samples}}}
  \sum_{i=0}^{n_{\text{samples}} - 1} \max_{j:y_{ij} = 1} \text{rank}_{ij}

damit\text{rank}_{ij} = \left\|\left\\\{k: \hat{f}\_{ik} \geq \hat{f}\_{ij} \right\\\}\right\|Ist definiert als. Angesichts der Definition des Rangesy_scoresDie Verbindungen werden unterbrochen, indem allen Verbindungen der maximale Rang zugewiesen wird.

Hier ist ein kleines Beispiel für die Verwendung dieser Funktion:

>>> import numpy as np
>>> from sklearn.metrics import coverage_error
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> coverage_error(y_true, y_score)
2.5

3.3.3.2 Durchschnittliche Konformitätsrate des Etikettenrangs

Die Funktion label_ranking_average_precision_score Conformance Label AAP. Diese Metrik ist mit der Funktion durchschnittlicher_Präzisionswert verknüpft, jedoch mit Präzision und Rückruf. Es basiert auf dem Konzept des Label Rankings statt. Die durchschnittliche Genauigkeit des Etikettenranges (LRAP) ist der Durchschnittswert jedes jeder Probe zugewiesenen Grand Truth-Etiketts und das Verhältnis von echten Etiketten zu Gesamtetiketten mit einer niedrigen Punktzahl. Diese Metrik verbessert Ihre Punktzahl, wenn Sie den Rang der mit jeder Stichprobe verknüpften Bezeichnung erhöhen können. Die erzielte Punktzahl ist immer genau größer als 0 und der beste Wert ist 1. Wenn es genau ein verwandtes Etikett pro Probe gibt, entspricht die durchschnittliche Anpassungsrate des Etikettenrankings dem durchschnittlichen inversen Rang (https://en.wikipedia.org/wiki/Mean_reciprocal_rank). Formal die Indexmatrix mit zwei Elementen der Grundwahrheitstabelle $ \ mathcal {R} ^ {n_ \ text {samples} \ times n_ \ text {labels}} $ und jedes Label $ \ hat {f} \ In mathcal {R} ^ {n_ \ text {samples} \ times n_ \ text {labels}} $ ist die durchschnittliche Genauigkeit wie folgt definiert:

LRAP(y, \hat{f}) = \frac{1}{n_{\text{samples}}}
  \sum_{i=0}^{n_{\text{samples}} - 1} \frac{1}{|y_i|}
  \sum_{j:y_{ij} = 1} \frac{|\mathcal{L}_{ij}|}{\text{rank}_{ij}}

\mathcal{L}\_{ij} = \left\\\{k: y_{ik} = 1, \hat{f}\_{ik} \geq \hat{f}\_{ij} \right\\\}, $\text{rank}_{ij} = \left|\left\{k: \hat{f}_{ik} \geq \hat{f}_{ij} \right\}\right| Und|\cdot|$Ist der Radix der l0 Norm oder Menge. Ein Beispiel für die Verwendung dieser Funktion ist unten dargestellt.

>>> import numpy as np
>>> from sklearn.metrics import label_ranking_average_precision_score
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_average_precision_score(y_true, y_score) 
0.416...

3.3.3.3. Rangverlust

label_ranking_loss Die Funktion ist die Anzahl der falsch geordneten Etikettenpaare, dh das wahre Etikett. Berechnet einen Rangverlust, der die Anzahl der Etikettenpaare mittelt, die eine niedrigere Punktzahl als das gefälschte Etikett haben und mit der Umkehrung des gefälschten Etiketts und des wahren Etiketts gewichtet werden. Der niedrigste erreichbare Rangverlust ist Null. Die Formel lautet 2 des Grundwahrheitslabels $ y \ in \ left \\ {0, 1 \ right \} \ ^ {n \ _ \ text {samples} \ times n \ _ \ text {label}} $ Gegeben ist die Basisindikatormatrix und die mit jedem Label verknüpfte Punktzahl $ \ hat {f} \ in \ mathbb {R} ^ {n \ _ \ text {samples} \ times n \ _ \ text {label}} $ Wenn der Rangverlust ist

\text{ranking\_loss}(y, \hat{f}) =  \frac{1}{n_{\text{samples}}}
  \sum_{i=0}^{n_{\text{samples}} - 1} \frac{1}{|y_i|(n_\text{labels} - |y_i|)}
  \left|\left\{(k, l): \hat{f}_{ik} < \hat{f}_{il}, y_{ik} = 1, y_{il} = 0 \right\}\right|

Hier,$ |\cdot| Ist \ell_0$Eine Norm oder Basis einer Menge.

Ein Beispiel für die Verwendung dieser Funktion ist unten dargestellt.

>>> import numpy as np
>>> from sklearn.metrics import label_ranking_loss
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_loss(y_true, y_score) 
0.75...
>>> # With the following prediction, we have perfect and minimal loss
>>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]])
>>> label_ranking_loss(y_true, y_score)
0.0

3.3.4. Regressionsmetrik

sklearn.metrics Module haben einige Verluste, Scores und Dienstprogramme zum Messen der Regressionsleistung. Implementiert die Funktion. mean_squared_error, mean_absolute_error /modules/generated/sklearn.metrics.mean_absolute_error.html#sklearn.metrics.mean_absolute_error), [EXPLAIN_Variance_score](http://scikit-learn.org/0.18/modules/generated/sklearn.metrics.explained_variance_score.html#s. Behandelt mehrere Ausgabefälle, z. B. Metrics.explained_variance_score) und r2_score. Einige wurden erweitert auf. Diese Funktionen verfügen über ein Schlüsselwortargument "Multioutput", das angibt, wie die Punktzahlen oder Verluste für einzelne Ziele gemittelt werden sollen. Der Standardwert ist "uniform_average". Dies gibt einen einheitlich gewichteten Durchschnitt für die Ausgabe an. Wenn ein "ndarray" mit der Form "(n_outputs,)" übergeben wird, wird der Eintrag als Gewicht interpretiert und ein entsprechender gewichteter Durchschnitt zurückgegeben. Wenn "Multioutput" "Draw_Werte" ist, werden alle einzelnen Scores und Verluste, die sich nicht geändert haben, in einer Reihe von Formen "(n_outputs,)" zurückgegeben. r2_score und EXPLAIN_Varianance_score akzeptieren einen zusätzlichen Wert "Varianzgewicht" für den Parameter "Multioutput". Diese Option führt zur Gewichtung einzelner Scores durch die Verteilung der entsprechenden Zielvariablen. Diese Einstellung quantifiziert global erfasste nicht skalierte Abweichungen. Wenn sich die Zielvariablen auf verschiedenen Skalen befinden, ist diese Bewertung wichtig, um besser zu erklären, dass die verteilten Variablen hoch sind. multioutput = 'Varianz_gewichtet' ist der Standardwert für r2_score aus Gründen der Abwärtskompatibilität. Dies wird sich in Zukunft in "uniform_average" ändern.

3.3.4.1. Erklärende Variablenbewertung

EXPLAIN_Varianance_score ist [Explanatory Variable Regression Score](https: //en.wikipedia) .org / wiki / Explained_variation) wird berechnet. Wenn $ \ hat {y} $ die geschätzte Zielausgabe ist, $ y $ die entsprechende (korrekte) Zielausgabe ist und $ Var $ das Quadrat der Standardabweichung ist, sind die erklärenden Variablen: Wird geschätzt als.

\texttt{explained_variance}(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}}

Die höchste Punktzahl ist 1,0, je niedriger der Wert, desto schlechter. Das Folgende ist ein Beispiel für die Verwendung der Funktion EXPLAIN_Varianz_Score.

>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)  
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='raw_values')
... 
array([ 0.967...,  1.        ])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
... 
0.990...

3.3.4.2 Durchschnittlicher absoluter Fehler

mean_absolute_error Die Funktion ist [mittlerer absoluter Fehler](https: //en.wikipedia) .org / wiki / Mean_absolute_error), berechnen Sie die Risikometrik, die dem erwarteten Wert des absoluten Fehlerverlusts oder des Normverlusts von $ l1 $ entspricht. Wenn $ \ hat {y} \ _i $ der vorhergesagte Wert der $ i $ -ten Stichprobe ist und $ y \ _i $ der entsprechende wahre Wert ist, dann ist $ n \ _ {\ text {samples}} $ Der geschätzte durchschnittliche absolute Fehler (MAE) ist definiert als:

\text{MAE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \left| y_i - \hat{y}_i \right|.

Das Folgende ist ein Beispiel für die Verwendung der Funktion mean_absolute_error.

>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput='raw_values')
array([ 0.5,  1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
... 
0.849...

3.3.4.3 Durchschnittlicher quadratischer Fehler

mean_squared_error Die Funktion ist ein quadratischer (sekundärer) Fehlerverlust oder erwarteter Verlust Berechnen Sie die entsprechende Risikometrik, den durchschnittlichen quadratischen Fehler (https://en.wikipedia.org/wiki/Mean_squared_error). Wenn $ \ hat {y} \ _i $ der vorhergesagte Wert der $ i $ -ten Stichprobe ist und $ y \ _i $ der entsprechende wahre Wert ist, dann ist $ n \ _ {\ text {samples}} $ Der geschätzte mittlere quadratische Fehler (MSE) ist definiert als:

\text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2.

Das Folgende ist ein Beispiel für die Verwendung der Funktion mean_squared_error.

>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred)  
0.7083...

--Beispiel:

3.3.4.4. Zentraler absoluter Fehler

median_absolute_error ist besonders interessant, da es robust gegen Ausreißer ist. Verluste werden berechnet, indem der Median aller absoluten Differenzen zwischen dem Ziel und der Prognose genommen wird. Wenn $ \ hat {y} \ _i $ der vorhergesagte Wert der $ i $ -ten Stichprobe ist und $ y \ _i $ der entsprechende wahre Wert ist, dann ist $ n \ _ {\ text {samples}} $ Der geschätzte absolute Fehler im Median (MedAE) ist definiert als:

\text{MedAE}(y, \hat{y}) = \text{median}(\mid y_1 - \hat{y}_1 \mid, \ldots, \mid y_n - \hat{y}_n \mid).

median_absolute_error unterstützt keine Mehrfachausgabe. Das folgende Beispiel zeigt die Verwendung der Funktion median_absolute_error.

>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5

3.3.4.5. R²-Punktzahl, Entscheidungsfaktor

r2_score Die Funktion ist [Decision Factor](https: //en.wikipedia. org / wiki / Coefficient_of_determination) Berechnet R². Dies liefert einen Indikator dafür, dass zukünftige Stichproben wahrscheinlich vom Modell vorhergesagt werden. Die höchstmögliche Punktzahl beträgt 1,0 und kann negativ sein (da sich das Modell willkürlich verschlechtern kann). In einem konstanten Modell, das Eingabemerkmale ignoriert und immer den erwarteten Wert von y vorhersagt, beträgt der R ^ 2-Score 0,0. Wenn $ \ hat {y} \ _i $ der vorhergesagte Wert der $ i $ -ten Stichprobe ist und $ y \ _i $ der entsprechende wahre Wert ist, dann ist $ n \ _ {\ text {samples}} $ Die geschätzte Punktzahl R² ist definiert als:

R^2(y, \hat{y}) = 1 - \frac{\sum_{i=0}^{n_{\text{samples}} - 1} (y_i - \hat{y}_i)^2}{\sum_{i=0}^{n_\text{samples} - 1} (y_i - \bar{y})^2}

$ \ bar {y} = \ frac {1} {n_ {\ text {samples}}} \ sum_ {i = 0} ^ {n_ {\ text {samples}} --1} y_i $. Das Folgende ist ein Beispiel für die Verwendung der Funktion r2_score.

>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred)  
0.948...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='variance_weighted')
... 
0.938...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='uniform_average')
... 
0.936...
>>> r2_score(y_true, y_pred, multioutput='raw_values')
... 
array([ 0.965...,  0.908...])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
... 
0.925...

--Beispiel:

3.3.5 Clustering-Metrik

Das Modul sklearn.metrics implementiert mehrere Verlust-, Score- und Dienstprogrammfunktionen. Weitere Informationen finden Sie im Abschnitt Bewertung der Clusterleistung (http://scikit-learn.org/0.18/modules/clustering.html#clustering-evaluation) im Abschnitt Instanzclustering und Biclustering-Bewertung von Biclustering (http: //: //). Siehe scikit-learn.org/0.18/modules/biclustering.html#biclustering-evaluation).

3.3.6. Dummy-Schätzung

Beim überwachten Lernen besteht ein einfacher Gesundheitscheck darin, den Schätzer mit einer einfachen empirischen Regel zu vergleichen. DummyClassifier implementiert einige dieser einfachen Strategien zur Klassifizierung. tun.

--stratified generiert zufällige Vorhersagen unter Berücksichtigung der Verteilung der Trainingssatzklassen. --most_frequent sagt immer die häufigsten Labels im Trainingssatz voraus. --prior sagt immer die Klasse voraus, die die Klasse maximiert (wie most_frequent), und pred_proba gibt die Klasse zuerst zurück. --uniform erzeugt zufällig und gleichmäßig eine Vorhersage. --constant ** Gibt immer eine vom Benutzer bereitgestellte konstante Bezeichnung als Vorhersage zurück. ** ** **

Bei all diesen Strategien ignoriert die "Vorhersage" -Methode die Eingabedaten vollständig. Um DummyClassifier zu erklären, erstellen wir zunächst einen unausgeglichenen Datensatz:

>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> y[y != 1] = -1
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

Als nächstes vergleichen wir die Genauigkeit von "SVC" und "most_frequent".

>>> from sklearn.dummy import DummyClassifier
>>> from sklearn.svm import SVC
>>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test) 
0.63...
>>> clf = DummyClassifier(strategy='most_frequent',random_state=0)
>>> clf.fit(X_train, y_train)
DummyClassifier(constant=None, random_state=0, strategy='most_frequent')
>>> clf.score(X_test, y_test)  
0.57...

Wir finden, dass SVC nicht viel besser ist als ein Dummy-Klassifikator. Jetzt ändern wir den Kernel:

>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)  
0.97...

Die Genauigkeit hat sich auf fast 100% verbessert. Wenn die Kosten der CPU nicht sehr hoch sind, wird eine Kreuzvalidierung empfohlen, um die Genauigkeit genauer beurteilen zu können. Weitere Informationen finden Sie im Abschnitt Kreuzvalidierung: Bewertung der geschätzten Leistung (http://qiita.com/nazoking@github/items/13b167283590f512d99a). Darüber hinaus wird dringend empfohlen, bei der Optimierung des Parameterraums die entsprechende Methode zu verwenden. Weitere Informationen finden Sie im Abschnitt Estimator HyperParameter Tuning (http://scikit-learn.org/0.18/modules/grid_search.html#grid-search). Im Allgemeinen kann etwas falsch sein, wenn die Genauigkeit des Klassifikators zu nahe am Zufall liegt. Funktionen sind nutzlos, Hyperparameter werden nicht richtig eingestellt, Klassifikatoren leiden unter Klassenungleichgewichten usw.

DummyRegressor implementiert außerdem vier einfache empirische Regeln für die Regression. Ich bin.

--mean sagt immer den Durchschnitt der Trainingsziele voraus. --median sagt immer den Medianwert der Trainingsziele voraus. --quantile sagt immer voraus, dass der Benutzer einen Teilungspunkt für das Trainingsziel bereitstellt. --constant gibt immer einen konstanten Wert zurück, den der Benutzer als Vorhersage angegeben hat.

Bei all diesen Strategien ignoriert die "Vorhersage" -Methode die Eingabedaten vollständig.

[scikit-learn 0.18 Benutzerhandbuch 3. Modellauswahl und -bewertung](http://qiita.com/nazoking@github/items/267f2371757516f8c168#3-%E3%83%A2%E3%83%87%E3%83] Von% AB% E3% 81% AE% E9% 81% B8% E6% 8A% 9E% E3% 81% A8% E8% A9% 95% E4% BE% A1)

© 2010 - 2016, Entwickler von Scikit-Learn (BSD-Lizenz).

Recommended Posts

[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 3.3. Modellbewertung: Quantifizieren Sie die Qualität der Vorhersage
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 4.8. Konvertieren Sie das Vorhersageziel (y)
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 3.4. Modellpersistenz
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 3.1. Kreuzvalidierung: Bewerten Sie die Leistung des Schätzers
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 3.5. Verifizierungskurve: Zeichnen Sie die Punktzahl, um das Modell zu bewerten
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 2.7. Erkennung von Neuheiten und Ausreißern
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 4.5. Zufällige Projektion
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 1.11. Ensemble-Methode
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 1.15. Isotonische Regression
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 4.2 Merkmalsextraktion
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 1.16. Wahrscheinlichkeitskalibrierung
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 1.13 Funktionsauswahl
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 2.8. Dichteschätzung
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 4.3. Datenvorverarbeitung
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 4.1. Pipeline- und Feature-Union: Kombination von Schätzern
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 4.4. Unüberwachte Dimensionsreduzierung
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 1.4. Support Vector Machine
[Übersetzung] scicit-learn 0.18 Tutorial Auswahl des richtigen Modells
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 2.5. Zerlegen von Signalen in Komponenten (Matrixzerlegungsproblem)
[Übersetzung] scikit-learn 0.18 Benutzerhandbuch 1.12. Mehrklassenalgorithmus und Mehrfachetikettenalgorithmus
Die Entscheidung von scikit-learn Wie man ein Holzmodell visualisiert
Japanische Übersetzung des e2fsprogs-Handbuchs
[Übersetzung] scikit-learn 0.18 Tutorial Inhaltsverzeichnis
Python-Simulation des Epidemiemodells (Kermack-McKendrick-Modell)
Japanische Übersetzung des man-db Handbuchs
Japanische Übersetzung des Util-Linux-Handbuchs
Japanische Übersetzung des iproute2-Handbuchs
Ich habe versucht, die Vorhersage-API des maschinellen Lernmodells von WordPress aus aufzurufen
Pandas Benutzerhandbuch "Zusammenführen und Verbinden und Verketten" (offizielles Dokument Japanische Übersetzung)