google übersetzte http://scikit-learn.org/0.18/modules/learning_curve.html [scikit-learn 0.18 Benutzerhandbuch 3. Modellauswahl und -bewertung](http://qiita.com/nazoking@github/items/267f2371757516f8c168#3-%E3%83%A2%E3%83%87%E3%83] Von% AB% E3% 81% AE% E9% 81% B8% E6% 8A% 9E% E3% 81% A8% E8% A9% 95% E4% BE% A1)

3.5 Validierungskurve: Zeichnen Sie die Punktzahl auf, um das Modell zu bewerten

Alle Schätzungen haben ihre Stärken und Schwächen. Sein Generalisierungsfehler kann in Bezug auf Vorspannung, Dispersion und Rauschen zerlegt werden. Der Schätzer ** Bias ** ist der durchschnittliche Fehler verschiedener Trainingssätze. Die ** Varianz ** des Schätzers gibt an, wie empfindlich er auf den sich ändernden Trainingssatz reagiert. Rauschen ist ein Merkmal von Daten.

Das folgende Diagramm zeigt die Funktion $ f (x) = \ cos (\ frac {3} {2} \ pi x) $ und ein verrauschtes Beispiel dieser Funktion. Wir verwenden drei verschiedene Bewertungsfunktionen, um diese Funktion anzupassen: Lineare Regression unter Verwendung polymorpher Merkmale erster, vierter und fünfzehnter Ordnung. Die anfänglichen Schätzungen sind so einfach, dass sie möglicherweise nicht sehr gut zur Stichprobe und zur tatsächlichen Funktion passen (hohe Verzerrung). Der zweite Schätzer nähert sich fast perfekt an. Der endgültige Schätzer nähert sich den Trainingsdaten perfekt an, passt aber nicht sehr gut zur wahren Funktion. Das heißt, es reagiert sehr empfindlich auf Änderungen der Trainingsdaten (hohe Streuung).

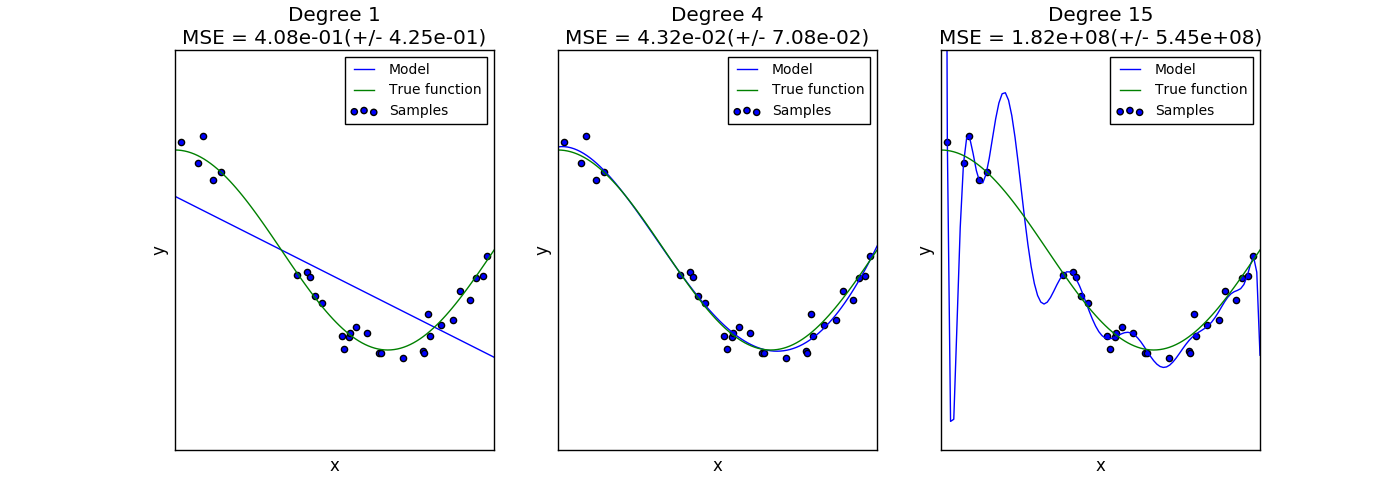
Bias und Varianz sind inhärente Eigenschaften von Schätzungen, und Trainingsalgorithmen und Hyperparameter sollten normalerweise so ausgewählt werden, dass sowohl Bias als auch Varianz so gering wie möglich sind ([Bias Deviation Dilemma](https: //). Siehe en.wikipedia.org/wiki/Bias-variance_dilemma)). Eine andere Möglichkeit, die Modellvarianz zu verringern, besteht darin, mehr Trainingsdaten zu verwenden. Wenn die tatsächliche Funktion jedoch zu komplex ist, um von einem Schätzer mit geringer Varianz angenähert zu werden, müssen mehr Trainingsdaten gesammelt werden. Bei einem einfachen eindimensionalen Problem wie dem in diesem Beispiel ist es leicht zu erkennen, ob der Schätzer unter Verzerrung oder Streuung leidet. In höherdimensionalen Räumen kann es jedoch sehr schwierig sein, das Modell zu visualisieren. Aus diesem Grund kann es nützlich sein, die folgenden Tools zu verwenden.

3.5.1 Verifizierungskurve

Zur Validierung des Modells benötigen Sie eine Bewertungsfunktion (siehe Modellbewertung: Quantifizieren der Qualität von Vorhersagen (http://qiita.com/nazoking@github/items/958426da6448d74279c7)). Zum Beispiel Klassifikatorgenauigkeit. Eine gute Möglichkeit zur Auswahl mehrerer Schätzer-Hyperparameter finden Sie unter Rastersuche oder einer ähnlichen Methode (siehe Anpassen von Schätzer-Hyperparametern (http://qiita.com/nazoking@github/items/09a4c63614797a6bd705). ), Und wählen Sie den Hyperparameter mit der höchsten Punktzahl im Validierungssatz oder in mehreren Validierungssätzen aus. Beachten Sie, dass, wenn Sie Ihre Hyperparameter basierend auf Ihrer Validierungsbewertung optimieren, Ihre Validierungsbewertung verzerrt ist und keine gute Generalisierungsschätzung mehr darstellt. Um eine gute Einschätzung der Verallgemeinerung zu erhalten, müssen Sie die Punktzahl in einem separaten Testsatz berechnen. Es kann jedoch nützlich sein, die Auswirkungen eines Hyperparameters auf die Trainings- und Validierungswerte aufzuzeichnen, um festzustellen, ob die Schätzungen für einige Hyperparameterwerte zu passend oder unzureichend sind. Verwenden Sie in diesem Fall die Funktion validation_curve:

>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge

>>> np.random.seed(0)
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]

>>> train_scores, valid_scores = validation_curve(Ridge(), X, y, "alpha",
...                                               np.logspace(-7, 3, 3))
>>> train_scores           
array([[ 0.94...,  0.92...,  0.92...],
       [ 0.94...,  0.92...,  0.92...],
       [ 0.47...,  0.45...,  0.42...]])
>>> valid_scores           
array([[ 0.90...,  0.92...,  0.94...],
       [ 0.90...,  0.92...,  0.94...],
       [ 0.44...,  0.39...,  0.45...]])

Wenn sowohl der Trainingswert als auch der Validierungswert niedrig sind, ist der Schätzer unzureichend. Wenn der Trainingswert hoch und der Validierungswert niedrig ist, ist der Schätzer überangepasst, andernfalls funktioniert er sehr gut. Es gibt normalerweise keine niedrigen Trainingswerte und hohen Validierungswerte. Alle drei Fälle finden Sie im folgenden Diagramm, in dem der SVM-Parameter $ \ gamma $ im Ziffern-Dataset geändert wird.

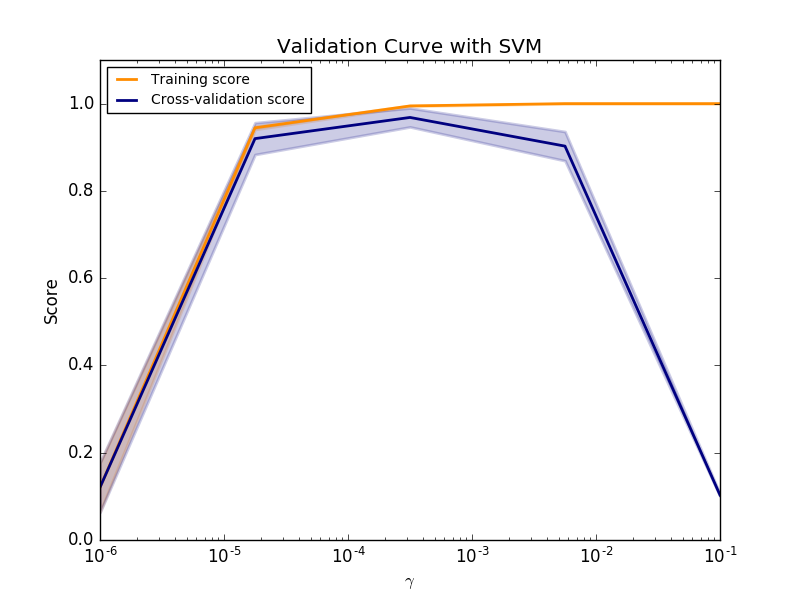
3.5.2 Lernkurve

Die Trainingskurve zeigt die Schätzervalidierung und die Trainingsergebnisse für eine unterschiedliche Anzahl von Trainingsmustern. Dies ist ein Tool, mit dem Sie feststellen können, inwieweit Sie vom Hinzufügen von Trainingsdaten profitieren können und ob der Schätzer weiterhin unter Streu- oder Verzerrungsfehlern leidet. Wenn sowohl die Validierungsbewertung als auch die Trainingsbewertung zu Werten konvergieren, die mit zunehmender Größe des Trainingssatzes zu niedrig sind, ist eine Erhöhung der Trainingsdaten nicht vorteilhaft. Sie können ein Beispiel in der Darstellung unten sehen. Native Bayes konvergieren im Allgemeinen zu einer niedrigen Punktzahl.

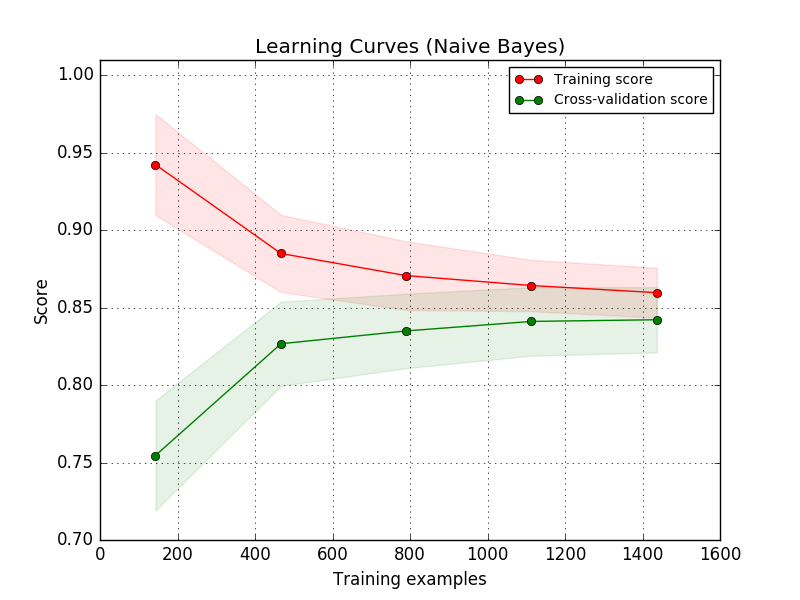
Möglicherweise müssen Sie die Parametrisierung eines Schätzers oder aktuellen Schätzers verwenden, um komplexere Konzepte zu lernen (dh weniger voreingenommen). Wenn der Trainingswert viel höher ist als der Validierungswert für die maximale Anzahl von Trainingsmustern, erhöht das Hinzufügen von Trainingsmustern höchstwahrscheinlich die Generalisierung. In der folgenden Darstellung sehen Sie, dass SVM von weiteren Trainingsbeispielen profitiert.

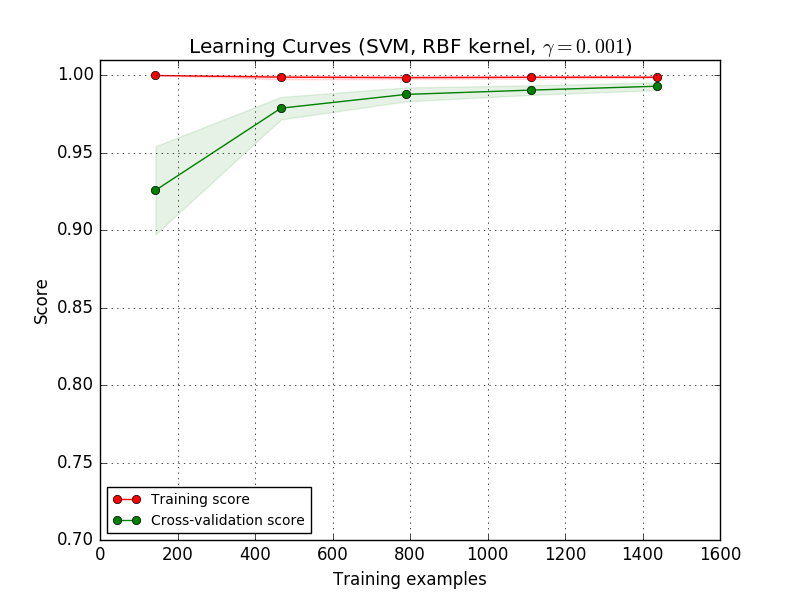
Mit der Funktion learning_curve wird eine solche Lernkurve (Beispiel verwendet) verwendet. Sie können die Werte generieren, die zum Zeichnen der Anzahl, der durchschnittlichen Punktzahl des Trainingssatzes und der durchschnittlichen Punktzahl des Validierungssatzes erforderlich sind.

>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC

>>> train_sizes, train_scores, valid_scores = learning_curve(
...     SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes            
array([ 50, 80, 110])
>>> train_scores           
array([[ 0.98...,  0.98 ,  0.98...,  0.98...,  0.98...],
       [ 0.98...,  1.   ,  0.98...,  0.98...,  0.98...],
       [ 0.98...,  1.   ,  0.98...,  0.98...,  0.99...]])
>>> valid_scores           
array([[ 1. ,  0.93...,  1. ,  1. ,  0.96...],
       [ 1. ,  0.96...,  1. ,  1. ,  0.96...],
       [ 1. ,  0.96...,  1. ,  1. ,  0.96...]])

[scikit-learn 0.18 Benutzerhandbuch 3. Modellauswahl und -bewertung](http://qiita.com/nazoking@github/items/267f2371757516f8c168#3-%E3%83%A2%E3%83%87%E3%83] Von% AB% E3% 81% AE% E9% 81% B8% E6% 8A% 9E% E3% 81% A8% E8% A9% 95% E4% BE% A1)

[PYTHON] [Übersetzung] scikit-learn 0.18 Benutzerhandbuch 3.5. Verifizierungskurve: Zeichnen Sie die Punktzahl, um das Modell zu bewerten

3.5 Validierungskurve: Zeichnen Sie die Punktzahl auf, um das Modell zu bewerten

3.5.1 Verifizierungskurve

3.5.2 Lernkurve