[PYTHON] [Übersetzung] scikit-learn 0.18 Benutzerhandbuch 1.11. Ensemble-Methode
google übersetzte http://scikit-learn.org/0.18/modules/ensemble.html [scikit-learn 0.18 Benutzerhandbuch 1. Überwachtes Lernen](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98 Von% E3% 81% 8D% E5% AD% A6% E7% BF% 92)
1.11. Ensemble-Methode
Das Ziel von ** Ensemble Learning ** ist es, die Vorhersagen mehrerer grundlegender Schätzer zu kombinieren, die mit einem bestimmten Lernalgorithmus erstellt wurden, um die Vielseitigkeit / Robustheit eines einzelnen Schätzers zu verbessern.
Das Lernen von Ensembles wird normalerweise in zwei Familien unterteilt.
-
** Die Mittelungsmethode ** basiert auf dem Prinzip, dass mehrere Schätzer unabhängig voneinander erstellt und ihre vorhergesagten Werte gemittelt werden. Im Durchschnitt sind kombinierte Schätzer aufgrund ihrer verringerten Streuung normalerweise besser als ein einzelner Schätzer.
-
Beispiel: Absackmethode, randomisierter Wald von Bäumen, ...
-
Im Gegensatz dazu erstellt die ** Boosting-Methode ** nacheinander Basisschätzer, um die Vorspannung des Kopplungsschätzers zu verringern. Die Motivation besteht darin, mehrere schwache Modelle zu kombinieren, um ein kraftvolles Ensemble zu schaffen.
-
Beispiel: AdaBoost, Gradient Tree Boost, ...
1.11.1. Bagging Meta Estimator
In dem Ensemble-Algorithmus baut die Bagging-Methode einen Blackbox-Schätzer auf einer zufälligen Teilmenge des ursprünglichen Trainingssatzes auf und bildet eine Klasse von Algorithmen, die die einzelnen Vorhersagen aggregieren, um die endgültige Vorhersage zu bilden. Diese Methoden führen Randomisierung in ihre Konstruktionsverfahren ein und verringern die Streuung von Basisschätzern (z. B. Entscheidungsbäumen), indem sie ein Ensemble erstellen. In vielen Fällen stellt die Absackmethode eine sehr einfache Möglichkeit dar, ein einzelnes Modell zu verbessern, ohne die zugrunde liegenden zugrunde liegenden Algorithmen anpassen zu müssen. Bagging-Methoden sind normalerweise starke und komplexe Modelle (z. B. vollständig), im Gegensatz zu den effektivsten Boosting-Methoden für schwache Modelle (z. B. flache Entscheidungsbäume), da sie eine Möglichkeit bieten, Überanpassungen zu reduzieren. Es ist am effektivsten im entfalteten Entscheidungsbaum. Es gibt viele Arten von Absackmethoden, aber die meisten unterscheiden sich je nachdem, wie Sie eine zufällige Teilmenge Ihres Trainingssatzes zeichnen.
- Dieser Algorithmus wird als Einfügen bezeichnet, wenn eine zufällige Teilmenge des Datensatzes als zufällige Teilmenge der Stichprobe gezeichnet wird. [B1999]
- Beim Ersetzen und Zeichnen der Probe wird diese Methode als Absacken bezeichnet. [B1996]
- Wenn eine zufällige Teilmenge eines Datensatzes als zufällige Teilmenge von Merkmalen gezeichnet wird, wird die Methode als zufällige Teilmenge bezeichnet. [H1998]
- Wenn der Basisschätzer auf einer Teilmenge von Stichproben und Merkmalen basiert, wird diese Methode als zufälliges Patch bezeichnet. [LG2012]
In scikit-learn lautet die Bagging-Methode BaggingClassifier Meta-Estimator (und BaggingRegressor) ) mit Parametern, die die Strategie zum Zeichnen einer zufälligen Teilmenge angeben. Als Eingabe wird ein benutzerdefinierter Basisschätzer verwendet. Insbesondere steuern "max_samples" und "max_features" die Größe der Teilmenge (in Bezug auf Beispiele und Merkmale), während "bootstrap" und "bootstrap_features" steuern, ob Beispiele und Merkmale ersetzt werden sollen. Wenn Sie eine Teilmenge der verfügbaren Stichproben verwenden, können Sie die Genauigkeit der Verallgemeinerung in der Out-of-Bag-Stichprobe abschätzen, indem Sie "oob_score = True" festlegen. Das folgende Snippet zeigt beispielhaft, wie ein Bagging-Ensemble aus KNeighborsClassifier-basierten Feature-Werten instanziiert wird, das aus einer zufälligen Teilmenge von 50% der Stichprobe und 50% des Features besteht.
>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
... max_samples=0.5, max_features=0.5)
-
Beispiel:
-
[Einzelschätzer und Absackung: Bias Dispersion Decomposition](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_bias_variance.html#sphx-glr-auto-examples-ensemble-plot-bias-variance- py)
-
Verweise
-
[B1999] L. Breiman, "Geben Sie eine kleine Stimme für große Datenbanken und Online-Klassifizierung ab" Machine Learning, 36 (1), 85-103, 1999
-
[B1996] L. Breiman, "Bagging Predictors", Machine Learning, 24 (2), 123-140, 1996 [H1998] T. Ho, "Random Subspace Method for Building Decision Forests", Pattern Analysis and Machine Intelligence, 20 (8), 832-844, 1998.
-
[LG2012] G. Louppe und P. Geurts, "Ensemble of Random Patches", Maschinelles Lernen und Wissensentdeckung in Datenbanken, 346-361, 2012.
1.11.2 Randomisierter Baumwald
sklearn.ensemble Das Modul verfügt über einen zufälligen [Entscheidungsbaum], den RandomForest-Algorithmus und die Extra-Trees-Methode. Es enthält zwei auf (http://scikit-learn.org/0.18/modules/tree.html#tree) basierende Mittelungsalgorithmen. Beide Algorithmen sind Störungs- und Kopplungstechniken, die speziell für Bäume entwickelt wurden [B1998]. Dies bedeutet, dass durch die Einführung von Zufälligkeit in die Klassifikatorkonstruktion ein vielfältiger Satz von Klassifikatoren erstellt wird. Ensemble-Vorhersagen werden als Durchschnittsvorhersagen für einzelne Klassifikatoren angegeben. Als weiterer Klassifizierer benötigt der Gesamtstrukturklassifizierer zwei Sequenzen. Spärliches oder dichtes Array X der Größe "[n_samples, n_features]" zum Halten von Trainingsmustern und Array Y der Größe "[n_samples]" zum Halten von Zielwerten (Klassenbezeichnungen) Trainingsmuster:
>>> from sklearn.ensemble import RandomForestClassifier
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, Y)
Ähnlich wie bei Decision Tree handelt es sich bei Tree Forest um Multi-Output-Problem. Es erstreckt sich auch auf /modules/tree.html#tree-multioutput) (wenn Y ein Array der Größe [n_samples, n_outputs] ist).
1.11.2.1 Zufälliger Wald
Random Forest (RandomForestClassifier Klasse und [RandomForestRegressor](http: // scikit-learn) In der Klasse .org / 0.18 / modules / generate / sklearn.ensemble.RandomForestRegressor.html (sklearn.ensemble.RandomForestRegressor) wurde jeder Baum im Ensemble mit einem Trainingssatzersatz (dh einem Bootstrap-Beispiel) gezeichnet. Es wird aus dem Beispiel erstellt. Wenn Sie beim Erstellen eines Baums einen Knoten teilen, ist die ausgewählte Aufteilung nicht mehr die beste Aufteilung aller Features. Stattdessen ist die ausgewählte Aufteilung die beste Aufteilung einer zufälligen Teilmenge von Features. Infolge dieser Zufälligkeit nimmt die Waldverzerrung normalerweise geringfügig zu (in Bezug auf die Verzerrung eines einzelnen nicht zufälligen Baums), aber aufgrund der Mittelung nimmt auch die Abweichung ab, wodurch normalerweise die erhöhte Verzerrung kompensiert wird. Sie erhalten nicht nur insgesamt ein besseres Modell. Im Gegensatz zum Originalpapier [B2001] kombiniert die Implementierung von Scicit-Learn Klassifizierer durch Mittelung probabilistischer Vorhersagen, anstatt dass jeder Klassifizierer für eine einzelne Klasse abstimmt.
1.11.2.2 Sehr zufälliger Baum
Hoch randomisierter Baum (ExtraTreesClassifier und [ExtraTreesRegressor](http :: //scikit-learn.org/0.18/modules/generated/sklearn.ensemble.ExtraTreesRegressor.html#sklearn.ensemble.ExtraTreesRegressor) Siehe Klasse)), wodurch die Zufälligkeit bei der Berechnung von Splits einen Schritt weiter geht. Ich werde. Wie bei zufälligen Gesamtstrukturen wird eine zufällige Teilmenge von Kandidatenmerkmalen verwendet, aber anstatt nach den bekanntesten Schwellenwerten zu suchen, werden Schwellenwerte für jedes Kandidatenmerkmal zufällig gezogen und diese werden zufällig generiert. Der höchste Wert des Schwellenwerts wird als Teilungsregel ausgewählt. Dies ermöglicht es normalerweise, die Varianz des Modells auf Kosten einer geringfügigen Erhöhung der Vorspannung sogar geringfügig zu verringern.
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import make_blobs
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.tree import DecisionTreeClassifier
>>> X, y = make_blobs(n_samples=10000, n_features=10, centers=100,
... random_state=0)
>>> clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2,
... random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean()
0.97...
>>> clf = RandomForestClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean()
0.999...
>>> clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean() > 0.999
True
1.11.2.3. Parameter
Die wichtigsten Parameter, die bei Verwendung dieser Methoden angepasst werden müssen, sind "n_estimators" und "max_features". Ersteres ist die Anzahl der Bäume. Größer ist besser, aber die Berechnung dauert länger. Denken Sie auch daran, dass das Überqueren einer erheblichen Anzahl von Bäumen die Ergebnisse nicht wesentlich verbessert. Letzteres ist die Größe einer zufälligen Teilmenge von Merkmalen, die beim Teilen von Knoten berücksichtigt werden müssen. Je niedriger der Wert ist, desto größer ist die Abnahme der Dispersion, aber desto größer ist die Zunahme der Vorspannung. Ein empirisch guter Standardwert ist "max_features = n_features" für Regressionsprobleme und "max_features = sqrt (n_features)" für Klassifizierungsaufgaben ("n_features" ist die Anzahl der Merkmale in den Daten). Das Setzen von "max_depth = None" in Kombination mit "min_samples_split = 1" (dh wenn der Baum vollständig erweitert ist) führt häufig zu guten Ergebnissen. Beachten Sie jedoch, dass diese Werte normalerweise nicht optimal sind und zu Modellen führen können, die viel RAM verbrauchen. Die besten Parameterwerte sollten immer gegenseitig validiert werden. Beachten Sie auch, dass zufällige Gesamtstrukturen standardmäßig das Bootstrap-Beispiel verwenden (bootstrap = True) und die Standardstrategie für zusätzliche Bäume das gesamte Dataset verwendet ( bootstrap = False). Bei Verwendung der Bootstrap-Stichprobe kann die Genauigkeit der Verallgemeinerung mit ausgelassenen oder aus der Tasche gezogenen Stichproben geschätzt werden. Um dies zu aktivieren, setzen Sie oob_score = True.
1.11.2.4. Parallelisierung
Schließlich bietet das Modul auch eine parallele Struktur von Bäumen und parallele Berechnungen von Vorhersagen mit dem Parameter n_jobs. Wenn n_jobs = k ist, wird die Berechnung in k Jobs aufgeteilt und auf k Kernen der Maschine ausgeführt. Wenn n_jobs = -1, werden alle auf dem Computer verfügbaren Kerne verwendet. Aufgrund des Kommunikationsaufwands zwischen den Prozessen ist die Beschleunigung möglicherweise nicht linear (dh die Verwendung eines k-Jobs ist leider nicht k-mal schneller). Erhebliche Beschleunigungen können erzielt werden, selbst wenn das Erstellen einer großen Anzahl von Bäumen oder sogar das Erstellen eines einzelnen Baums viel Zeit erfordert (z. B. ein großer Datensatz).
-
Beispiel:
-
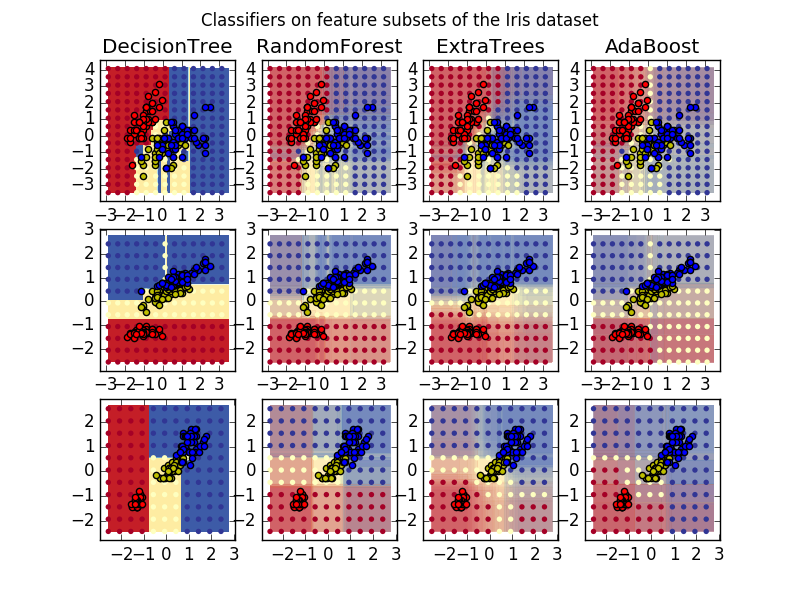
[Zeichnen Sie die Entscheidungsebene des Baumensembles in den Iris-Datensatz](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_forest_iris.html#sphx-glr-auto-examples-ensemble-plot-forest -iris-py)
-
[Pixelbedeutung in parallelen Wäldern von Bäumen](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_forest_importances_faces.html#sphx-glr-auto-examples-ensemble-plot-forest-importances -faces-py)
-
Verweise
-
[B2001] Breiman, "Random Forest", Machine Learning, 45 (1), 5-32, 2001.
- [B1998] Breiman、 "Arcing Classifiers"、Annals of Statistics 1998
-
[GEW2006] P. Geurts, D. Ernst. Und L. Wehenkel, "Super Randomized Trees", Machine Learning, 63 (1), 3-42, 2006.
1.11.2.5. Bewertung der Wichtigkeit der Merkmalsmenge
Der relative Rang (dh die Tiefe) eines Merkmals, das als Entscheidungsknoten im Baum verwendet wird, kann verwendet werden, um die relative Bedeutung dieses Merkmals für die Vorhersagbarkeit der Zielvariablen zu bewerten. Die oben im Baum verwendeten Merkmale tragen zur endgültigen prädiktiven Bestimmung des größeren Teils der Eingabestichprobe bei. Daher kann * der erwartete Anteil der Proben, zu denen sie beitragen *, als Schätzung der relativen Bedeutung * der * Merkmale (erklärende Variablen) verwendet werden. Durch * Mittelung * dieser erwarteten Aktivitätsraten über mehrere randomisierte Bäume kann die * Varianz * solcher Schätzungen reduziert * und für die Merkmalsauswahl verwendet werden. .. Das folgende Beispiel bezieht sich auf jedes Pixel einer Gesichtserkennungsaufgabe mit dem Modell ExtraTreesClassifier. Zeigt eine farbcodierte Darstellung des relativen Messwerts.
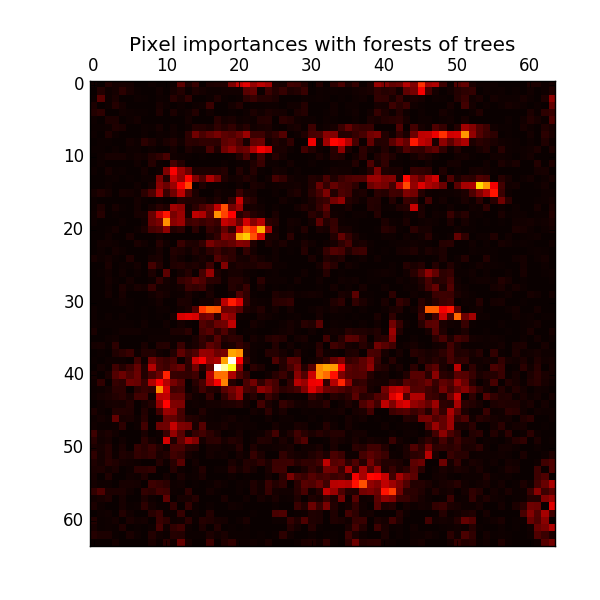
In der Praxis werden diese Schätzungen im angepassten Modell als Attribut mit dem Namen "feature_importances_" gespeichert. Dies ist ein Array mit positiven Werten für die Form "(n_features,)" und einer Summe von 1,0. Je höher der Wert, desto wichtiger ist der Beitrag der Übereinstimmungsfunktion zur Vorhersagefunktion.
- Beispiel:
- [Pixelbedeutung in parallelen Wäldern von Bäumen](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_forest_importances_faces.html#sphx-glr-auto-examples-ensemble-plot-forest-importances -faces-py)
- Importieren von Features in die Baumstruktur
1.11.2.6 Vollständig zufällige Baumeinbettung
RandomTreesEmbedding implementiert eine unbeaufsichtigte Datentransformation. RandomTreesEmbedding verwendet eine vollständig zufällige Baumstruktur und codiert die Daten anhand des Index des Blattes, an dem die Datenpunkte enden. Dieser Index wird eins zu eins K codiert, was zu einer höherdimensionalen, spärlichen Binärcodierung führt. Diese Kodierung wird sehr effizient berechnet und kann als Grundlage für andere Lernaufgaben verwendet werden. Codegröße und Spärlichkeit können durch Auswahl der Anzahl der Bäume und der maximalen Tiefe pro Baum beeinflusst werden. Für jeden Baum im Ensemble enthält die Codierung einen Eintrag. Die maximale Codierungsgröße beträgt "n_estimators * 2 ** max_depth". Dies ist die maximale Anzahl von Blättern im Wald. Die Transformation führt eine implizite nichtparametrische Dichteschätzung durch, da benachbarte Datenpunkte wahrscheinlich im selben Blatt des Baums liegen.
- Beispiel:
- [Hash-Konvertierung unter Verwendung eines vollständig zufälligen Baums](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_random_forest_embedding.html#sphx-glr-auto-examples-ensemble-plot-random-forest-embedding -py)
- [Vielfältiges Lernen handgeschriebener Zahlen: Lokale lineare Einbettung, Isomap ...](http://scikit-learn.org/0.18/auto_examples/manifold/plot_lle_digits.html#sphx-glr-auto-examples-manifold-plot -lle-digits-py) vergleicht nichtlineare Dimensionsreduktionstechniken für handgeschriebene Zahlen.
- Charakteristische Transformation nach Baumensemble Vergleicht einen überwachten Baum mit einer nicht verwalteten baumbasierten Feature-Transformation.
Siehe auch: Manifold Learning (http://scikit-learn.org/0.18/modules/manifold.html#manifold) Die Technik hilft auch dabei, eine nichtlineare Darstellung des Feature-Space abzuleiten. Diese Ansätze konzentrieren sich auch auf die Dimensionsreduzierung.
1.11.3. AdaBoost
Das Modul sklearn.ensemble ist ein allgemeiner Boosting-Algorithmus, der 1995 von Freund und Schapire eingeführt wurde. Beinhaltet AdaBoost [FS1995]. Das Kernprinzip von AdaBoost besteht darin, eine Folge schwacher Lernender (ein Modell, das etwas besser ist als eine zufällige Vermutung, z. B. ein kleiner Entscheidungsbaum) an eine iterativ modifizierte Version der Daten anzupassen. Die Vorhersagen von allen werden mit einer gewichteten Mehrheit (oder Summe) kombiniert, um die endgültige Vorhersage zu erzeugen. Die Datenänderung in jeder Boosting-Iteration besteht darin, Gewichte $ w_1, w_2, ..., w_N $ auf jedes der Trainingsmuster anzuwenden. Zu Beginn werden alle diese Gewichte auf $ w_i = 1 / N $ gesetzt. Der erste Schritt besteht also darin, den schwachen Lernenden einfach mit den Originaldaten zu trainieren. Bei jeder Iteration werden die Stichprobengewichte einzeln geändert und der Trainingsalgorithmus wird erneut auf die neu gewichteten Daten angewendet. In einem bestimmten Schritt haben Trainingsbeispiele, die durch das im vorherigen Schritt hervorgerufene verstärkte Modell falsch vorhergesagt wurden, ein erhöhtes Gewicht, und diejenigen, die korrekt vorhergesagt wurden, haben ein verringertes Gewicht. Im Verlauf der Iterationen sind schwer vorhersehbare Fälle immer mehr betroffen. Jeder nachfolgende schwache Lernende ist gezwungen, sich auf die Beispiele zu konzentrieren, die der schwache Lernende vor der Sequenz [HTF] übersehen hat.
- AdaBoost kann sowohl für Klassifizierungs- als auch für Regressionsprobleme verwendet werden.
- In der Mehrklassenklassifizierung [AdaBoostClassifier](http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.AdaBoostClassifier.html#sklearn], das AdaBoost-SAMME und AdaBoost-SAMME.R [ZZRH2009] implementiert. .ensemble.AdaBoostClassifier).
- Verwenden Sie für die Regression AdaBoostRegressor, das AdaBoost.R2 [D1997] implementiert.
1.11.3.1. Verwendung
Das folgende Beispiel zeigt, wie Sie mit dem AdaBoost-Klassifikator unter Verwendung von 100 schwachen Lernenden trainieren.
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import AdaBoostClassifier
>>> iris = load_iris()
>>> clf = AdaBoostClassifier(n_estimators=100)
>>> scores = cross_val_score(clf, iris.data, iris.target)
>>> scores.mean()
0.9...
Die Anzahl der schwachen Lernenden wird durch den Parameter "n_estimators" gesteuert. Der Parameter "learning_rate" steuert den Beitrag des schwachen Lernenden zur endgültigen Kombination. Standardmäßig ist der schwache Lernende Decision Stock. Sie können einen schwachen Lernenden mit dem Parameter base_estimator angeben. Die wichtigsten Parameter, die für gute Ergebnisse angepasst werden müssen, sind "n_estimator" und die Komplexität der Basisschätzung (z. B. für Tiefenbäume die minimal erforderliche Anzahl von Stichproben in der Tiefe "max_depth" oder das Blatt "min_samples_leaf"). ist.
-
Beispiel:
-
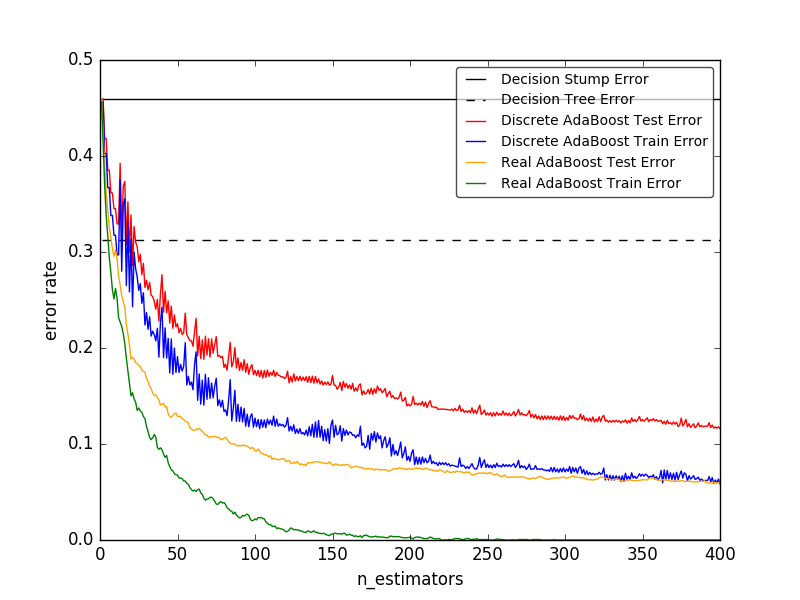
Diskrete vs. reelle Zahl AdaBoost Verwendet AdaBoost-SAMME und AdaBoost-SAMME.R, um die Klassifizierungsfehler von Entscheidungsstümpfen, Entscheidungsbäumen und verstärkten Entscheidungsstümpfen zu vergleichen.
-
Ada Boosted Decision Trees für mehrere Klassen Zeigt die Leistung von AdaBoost-SAMME und AdaBoost-SAMME.R bei Problemen mit mehreren Klassen an.
-
2 Klassen von AdaBoost ist AdaBoost-py Verwenden Sie SAMME, um die Werte für Entscheidungsgrenze und Entscheidungsfunktion für ein nicht linear trennbares Zwei-Klassen-Problem anzuzeigen.
-
Decision Tree Regression von AdaBoost ist AdaBoost Zeigt die Regression durch den .R2-Algorithmus an.
-
Verweise
-
[FS1995] Y. Freund und R. Schapire, "Entscheidende Verallgemeinerung des Online-Lernens und seine Anwendung auf die Steigerung", 1997.
-
[ZZRH2009] J. Zhu, H. Zou, S. Rosset, T. Hastie. "Multiclass Ada Boost", 2009.
-
[D1997] Drucker. "Verbesserung der Rücklaufmaschine unter Verwendung der Boosting-Technologie", 1997.
-
[HTF] T. Hastie, R. Tibshirani und J. Friedman, "Elements of Statistical Learning Ed. 2", Springer, 2009.
1.11.4 Gradientenbaum-Boost
Gradient Tree Boost (https://en.wikipedia.org/wiki/Gradient_boosting) oder Gradient Boost Regression Tree (GBRT) ist eine Verallgemeinerung, die zu jeder teilbaren Verlustfunktion führt. GBRT ist ein genaues und effektives Standardverfahren, das sowohl für Regressions- als auch für Klassifizierungsprobleme verwendet werden kann. Das Gradient Tree Boosting-Modell wird in einer Vielzahl von Bereichen verwendet, einschließlich Web-Suchrankings und Ökologie.
- Die Vorteile von GBRT sind:
- Natürliche Behandlung gemischter Daten (= heterogene Merkmale)
- Vorhersagekraft
- Robustheit gegenüber Ausreißern im Ausgaberaum (aufgrund der robusten Verlustfunktion)
- Die Nachteile von GBRT sind:
- Aufgrund der sequentiellen Natur des Boostings kann es kaum parallelisiert werden.
Das Modul sklearn.ensemble bietet Methoden zur Klassifizierung und Regression mit gradientenverstärkten Regressionsbäumen. Bietet an.
1.11.4.1. Klassifizierung
GradientBoostingClassifier unterstützt sowohl die binäre als auch die Klassifizierung mehrerer Klassen. Das folgende Beispiel zeigt, wie ein Gradientenverstärkungsklassifikator als schwacher Lernender mit 100 bestimmten Belastungen angepasst wird.
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.913...
Die Anzahl der schwachen Lernenden (dh Regressionsbäume) wird durch den Parameter "n_estimators" gesteuert. Legen Sie für jede Baumgröße (http://scikit-learn.org/0.18/modules/ensemble.html#gradient-boosting-tree-size) die Baumtiefe mit "max_depth" oder "max_leaf_nodes" fest Sie kann gesteuert werden, indem Sie die Anzahl der Blattknoten mit einstellen. learning_rate ist ein Hyperparameter des Bereichs (0.0, 1.0]`, der die Überanpassung durch [shrink] steuert (http://scikit-learn.org/0.18/modules/ensemble.html#gradient-boosting-shrinkage). ist.
** Hinweis: ** Eine Klassifizierung mit zwei oder mehr Klassen erfordert die Induktion eines Regressionsbaums "n_classes" bei jeder Iteration, sodass die Gesamtzahl der Induktionsbäume gleich "n_classes * n_estimators" ist. Für Datensätze mit vielen Klassen anstelle von GradientBoostingClassifier Wir empfehlen dringend die Verwendung von (http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.RandomForestClassifier.html#sklearn.ensemble.RandomForestClassifier).
1.11.4.2. Zurück
GradientBoostingRegressor ist eine Vielzahl von Regressionsverlusten, die durch das Argument "Verlust" angegeben werden können. Funktionen](http://scikit-learn.org/0.18/modules/ensemble.html#gradient-boosting-loss) wird unterstützt. Die Standardverlustfunktion für die Regression ist das kleinste Quadrat ('ls').
>>> import numpy as np
>>> from sklearn.metrics import mean_squared_error
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
>>> X_train, X_test = X[:200], X[200:]
>>> y_train, y_test = y[:200], y[200:]
>>> est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
... max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
>>> mean_squared_error(y_test, est.predict(X_test))
5.00...
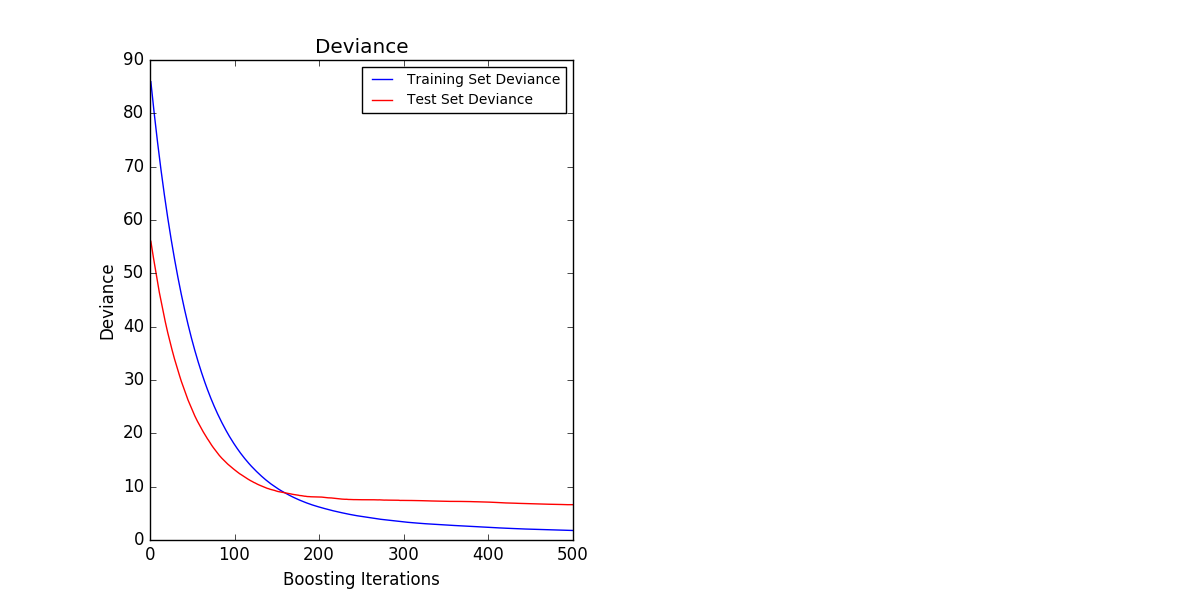
Die folgende Abbildung zeigt den Bostoner Immobilienpreisdatensatz (sklearn.datasets.load_boston). ) Mit minimalem Quadratverlust und einem 500-basierten Lernenden angewendet [GradientBoostingRegressor](http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble. Das Ergebnis von GradientBoostingRegressor wird angezeigt. Das Diagramm links zeigt den Zug und den Testfehler bei jeder Iteration. Der Zugfehler bei jeder Iteration wird im Attribut train_score_ des Gradientenverstärkungsmodells gespeichert. Der Testfehler bei jeder Iteration gibt einen Generator zurück, der eine Vorhersage für jede Stufe [staged_predict] generiert (http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble). Es kann mit der Methode GradientBoostingRegressor.staged_predict) abgerufen werden. Sie können ein solches Diagramm verwenden, um die optimale Anzahl von Bäumen (n_estimators) durch frühzeitiges Anhalten zu bestimmen. Das Diagramm rechts zeigt die Feature-Importe, die mit der Eigenschaft feature_importances_ abgerufen werden können.
1.11.4.3. Zusätzliches Lernen
GradientBoostingRegressor und [GradientBoostingClassifier](http://scorgit- /modules/generated/sklearn.ensemble.GradientBoostingClassifier.html#sklearn.ensemble.GradientBoostingClassifier) unterstützen beide warm_start = True. Auf diese Weise können Sie einem bereits angepassten Modell eine Schulung hinzufügen.
>>> _ = est.set_params(n_estimators=200, warm_start=True) # set warm_start and new nr of trees
>>> _ = est.fit(X_train, y_train) # fit additional 100 trees to est
>>> mean_squared_error(y_test, est.predict(X_test))
3.84...
1.11.4.4. Kontrolle der Baumgröße
Die Größe des auf einem Regressionsbaum basierenden Studieninstruments definiert den Grad der variablen Interaktion, der vom Gradientenverstärkungsmodell erfasst wird. Im Allgemeinen können Bäume mit einer Tiefe von "h" Wechselwirkungen vom Grad "h" erfassen. Es gibt zwei Möglichkeiten, die Größe einzelner Regressionsbäume zu steuern.
Die Angabe von "max_depth = h" vervollständigt einen Binärbaum mit einer Tiefe von "h". Ein solcher Baum hat (bis zu) einen Blattknoten von "2 ** h" und einen geteilten Knoten von "2 ** h-1".
Alternativ können Sie den Parameter max_leaf_nodes verwenden, um die Baumgröße durch Angabe der Anzahl der Blattknoten zu steuern. In diesem Fall wächst der Baum mithilfe der Best-First-Suche, wobei der Knoten mit den am besten verbesserten Verunreinigungen zuerst erweitert wird. Ein Baum mit "max_leaf_nodes = k" hat "k-1" geteilte Knoten und kann Interaktionen bis zu "max_leaf_nodes-1" modellieren.
Wir haben festgestellt, dass "max_leaf_nodes = k" Ergebnisse liefert, die mit "max_depth = k-1" vergleichbar sind, aber das Training ist viel schneller, jedoch auf Kosten etwas höherer Trainingsfehler. Der Parameter "max_leaf_nodes" entspricht der Variablen "J" im Kapitel "Gradient Boost" von [F2001] und bezieht sich auf den Parameter "Interaction.depth" des gbm-Pakets des R mit "max_leaf_nodes == Interaction.depth + 1".
1.11.4.5. Mathematische Vorschrift
GBRT betrachtet ein additives Modell der Form:
F(x) = \sum_{m=1}^{M} \gamma_m h_m(x)
Wobei $ h_m (x) $ eine Basisfunktion ist, die im Zusammenhang mit dem Boosten normalerweise als schwacher Lernender bezeichnet wird. Gradient Tree Boosting verwendet eine feste Größe Entscheidungsbaum als schwachen Lernenden. Der Entscheidungsbaum verfügt über mehrere Funktionen, die zum Verbessern nützlich sind, um Ihre Fähigkeit zu verbessern, mit gemischten Daten zu arbeiten und komplexe Funktionen zu modellieren. Wie andere Boosting-Algorithmen erstellt GBRT das Addierermodell in der Vorwärtsphase.
F_m(x) = F_{m-1}(x) + \gamma_m h_m(x)
In jeder Phase ist der Entscheidungsbaum $ h_m (x) $ die Verlustfunktion $ L $ bei dem aktuellen Modell $ F_ {m-1} $ und seiner Anpassung $ F_ {m-1} (x_i) $. Wird zum Minimieren ausgewählt.
F_m(x) = F_{m-1}(x) + \arg\min_{h} \sum_{i=1}^{n} L(y_i,
F_{m-1}(x_i) - h(x))
Das ursprüngliche Modell $ F_ {0} $ ist problemspezifisch und wählt normalerweise den Durchschnitt der Zielwerte für die Regression mit minimalem Quadrat.
Hinweis: Das ursprüngliche Modell kann auch mit dem Argument init angegeben werden. Das übergebene Objekt muss Anpassung und Vorhersage implementieren.
Gradient Boost versucht, dieses Minimierungsproblem numerisch durch den steilsten Abstieg zu lösen. Die steilste Abstiegsrichtung ist der negative Gradient der Verlustfunktion, der vom aktuellen Modell $ F_ {m-1} $ ausgewertet wird und für jede teilbare Verlustfunktion berechnet werden kann.
F_m(x) = F_{m-1}(x) + \gamma_m \sum_{i=1}^{n} \nabla_F L(y_i,
F_{m-1}(x_i))
Wenn Sie die Zeilenlänge angeben und die Schrittlänge $ \ gamma_m $ auswählen,
\gamma_m = \arg\min_{\gamma} \sum_{i=1}^{n} L(y_i, F_{m-1}(x_i)
- \gamma \frac{\partial L(y_i, F_{m-1}(x_i))}{\partial F_{m-1}(x_i)})
Die Algorithmen zur Regression und Klassifizierung unterscheiden sich nur in der verwendeten spezifischen Verlustfunktion.
1.11.4.5.1. Verlustfunktion
Die folgenden Verlustfunktionen werden unterstützt und können mit dem Parameter "Verlust" angegeben werden.
- Rückkehr
- Minimales Quadrat (
'ls'): Natürliche Auswahl der Regression aufgrund hervorragender Recheneigenschaften. Das Ausgangsmodell ergibt sich aus dem Durchschnitt der Zielwerte. - Minimale absolute Abweichung (
'lad'): Robustros-Funktion der Regression. Das Ausgangsmodell ergibt sich aus dem mittleren Zielwert. - Huber (
'huber'): Eine weitere Robustros-Funktion, die das kleinste Quadrat und die minimale absolute Abweichung kombiniert. Verwenden Sie "Alpha", um die Empfindlichkeit in Bezug auf Konturen zu steuern (Details siehe [F2001]). - Quantil (
'Quantil'): Verlustfunktion der Divisionsregression. Verwenden Sie0 <alpha <1, um die Anzahl der Brüche anzugeben. Mit dieser Verlustfunktion können Sie ein Vorhersageintervall erstellen (Vorhersageintervall für die Gradientenverstärkungsregression (http://scikit-learn.org/0.18/auto_examples/ensemble/plot_gradient_boosting_quantile.html#sphx-glr-)). (siehe Auto-Beispiele-Ensemble-Plot-Gradient-Boosting-Quantile-Py)). - Klassifizierung
- Binäre Klassifizierung ("Abweichung"): Negative binäre logarithmische Wahrscheinlichkeitsverlustfunktion für die Binomialklassifizierung (liefert eine Wahrscheinlichkeitsschätzung). Das ursprüngliche Modell ergibt sich aus dem Log Odds Ratio.
- Polygonale Abweichung ("Abweichung"): Negativer Polynomlogarithmus für die Klassifizierung mehrerer Klassen mit sich gegenseitig ausschließender Wahrscheinlichkeitsverlustfunktion der Klasse "n_classes". Es bietet eine probabilistische Schätzung. Das anfängliche Modell ist durch die Vorwahrscheinlichkeit jeder Klasse gegeben. Bei jeder Iteration müssen Sie einen Regressionsbaum erstellen, der GBRT für Datasets mit vielen Klassen ziemlich ineffizient macht.
- Exponentieller Verlust (
'exponentiell'): Wie AdaBoostClassifier Verlustfunktion. Beispiele, die fälschlicherweise als "Abweichung" bezeichnet werden, sind nicht sehr stark. Kann nur für die binäre Klassifizierung verwendet werden.
1.11.4.6. Normalisierung
1.11.4.6.1. Schrumpfung
[F2001] schlug eine einfache Regularisierungsstrategie vor, die den Beitrag jedes schwachen Lernenden um einen Faktor skaliert. $ \ nu $:
F_m(x) = F_{m-1}(x) + \nu \gamma_m h_m(x)
Der Parameter $ \ nu $ wird auch als ** Lernrate ** bezeichnet, da er die Schrittlänge der Gradientenabstiegsprozedur skaliert. Sie kann mit dem Parameter "learning_rate" eingestellt werden.
Der Parameter learning_rate interagiert stark mit dem Parameter n_estimators, der der Anzahl der schwachen Lernenden entspricht. Je kleiner der Wert von "learning_rate" ist, desto schwächer werden die Lernenden benötigt, um konstante Trainingsfehler aufrechtzuerhalten. Empirische Belege zeigen, dass kleinere Werte für learning_rate Testfehler verbessern. [HTF2009] empfiehlt, die Lernrate auf eine kleine Konstante einzustellen (z. B. "Lernrate <= 0,1") und "n_Stimatoren" durch vorzeitiges Stoppen auszuwählen. Weitere Informationen zur Interaktion zwischen learning_rate und n_estimators finden Sie in [R2007].
1.11.4.6.2. Unterabtastung
[F1999] schlug einen probabilistischen Gradientenschub vor, der den Gradientenschub mit dem Bootstrap-Durchschnitt (Absacken) kombiniert. Bei jeder Iteration wird der Basisklassifizierer an dem Bruchteil "Teilstichprobe" der verfügbaren Trainingsdaten trainiert. Teilproben werden ersatzlos gezogen. Ein typischer Wert für "Teilstichprobe" ist 0,5. Die folgende Abbildung zeigt die Auswirkung von Schrumpfung und Unterabtastung auf die Modellanpassung. Sie können deutlich sehen, dass sich die Kontraktion nicht zusammenzieht. Eine Unterabtastung mit Schrumpfung kann die Genauigkeit des Modells weiter verbessern. Andererseits funktioniert eine Unterabtastung ohne Schrumpfung nicht sehr gut.
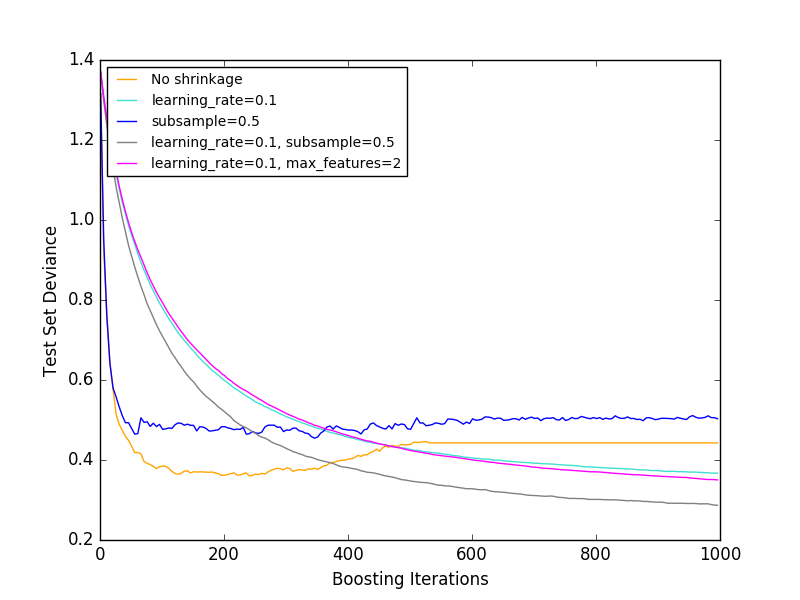
Eine andere Strategie zur Reduzierung der Streuung ähnelt der zufälligen Aufteilung mit RandomForestClassifier. Es dient zur Unterabtastung der Merkmalsmenge. Die Anzahl der unterabgetasteten Features kann mit dem Parameter "max_features" gesteuert werden.
Hinweis: Durch Verringern des Werts von max_features kann die Laufzeit erheblich verkürzt werden.
Die probabilistische Gradientenverstärkung ermöglicht es, Out-of-Bag-Schätzungen von Testabweichungen zu berechnen, indem die Verbesserung der Abweichungen für Beispiele berechnet wird, die nicht in der Bootstrap-Stichprobe enthalten sind (dh Out-of-Bag-Beispiele). Verbesserungen werden im Attribut "oob_improvement_" gespeichert. oob_improvement_ [i] behält die Verbesserung des OOB-Probenverlusts bei, wenn die i-te Stufe zur aktuellen Vorhersage hinzugefügt wird. Sie können Out-of-Bag-Schätzungen für die Modellauswahl verwenden, z. B. um die optimale Anzahl von Iterationen zu bestimmen. OOB-Schätzer sind normalerweise sehr pessimistisch. Daher wird empfohlen, stattdessen die gegenseitige Validierung zu verwenden und OOB nur dann zu verwenden, wenn die gegenseitige Validierung zu lange dauert.
- Beispiel:
- Gradient Boosting Regularization
- Schätzung des Gradientenschubs aus der Tasche
- Random Forest OOB Error
1.11.4.7. Interpretation
Einzelne Entscheidungsbäume können einfach durch einfache Visualisierung der Baumstruktur interpretiert werden. Das Gradientenverstärkungsmodell enthält jedoch Hunderte von Rückgabebäumen und kann durch visuelle Inspektion einzelner Bäume nicht einfach interpretiert werden. Glücklicherweise wurden viele Techniken vorgeschlagen, um Gradientenverstärkungsmodelle zusammenzufassen und zu interpretieren.
1.11.4.7.1. Bedeutung von Funktionen
In vielen Fällen tragen Funktionen nicht gleichmäßig zur Vorhersage der Zielantwort bei. In vielen Fällen sind die meisten Funktionen tatsächlich irrelevant. Bei der Interpretation eines Modells ist die erste Frage normalerweise, was ihre Hauptmerkmale sind und wie sie zur Vorhersage der Zielantwort beitragen.
Der einzelne Entscheidungsbaum führt im Wesentlichen eine Merkmalsauswahl durch Auswahl der geeigneten Teilungspunkte durch. Diese Informationen können verwendet werden, um die Wichtigkeit jedes Merkmals zu messen. Die Grundidee ist, dass das Feature umso wichtiger wird, je öfter ein Feature an einem Baumsplitpunkt verwendet wird. Dieses wichtige Konzept kann auf ein Entscheidungsbaum-Ensemble erweitert werden, indem einfach die Merkmalsbedeutung jedes Baums gemittelt wird (weitere Informationen finden Sie unter Schweregradbewertung (http: // scikit-)). Siehe learn.org/0.18/modules/ensemble.html#random-forest-feature-importance).
Auf die Feature-Wichtigkeitsbewertung des Fit-Gradienten-Boosting-Modells kann über die Eigenschaft feature_importances_ zugegriffen werden.
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_
array([ 0.11, 0.1 , 0.11, ...
- Beispiel:
- Gradient Boost Regression
1.11.4.7.2. Teilweise abhängig
Das Partial Dependency Plot (PDP) zeigt die Abhängigkeit zwischen der Zielantwort und einer Reihe von "Ziel" -Features, die die Werte aller anderen Features ("komplementäre" Features) begrenzen. Intuitiv können wir die partielle Abhängigkeit als Funktion des "Ziel" -Features [2] und als erwartete Zielantwort [1] interpretieren. Aufgrund der Einschränkungen der menschlichen Wahrnehmung muss die Größe des Zielmerkmalsatzes klein sein (normalerweise eins oder zwei), sodass das Zielmerkmal normalerweise aus den wichtigsten Merkmalen ausgewählt wird. Die folgende Abbildung zeigt vier unidirektionale und unidirektionale, teilweise abhängige Diagramme des kalifornischen Wohndatensatzes.
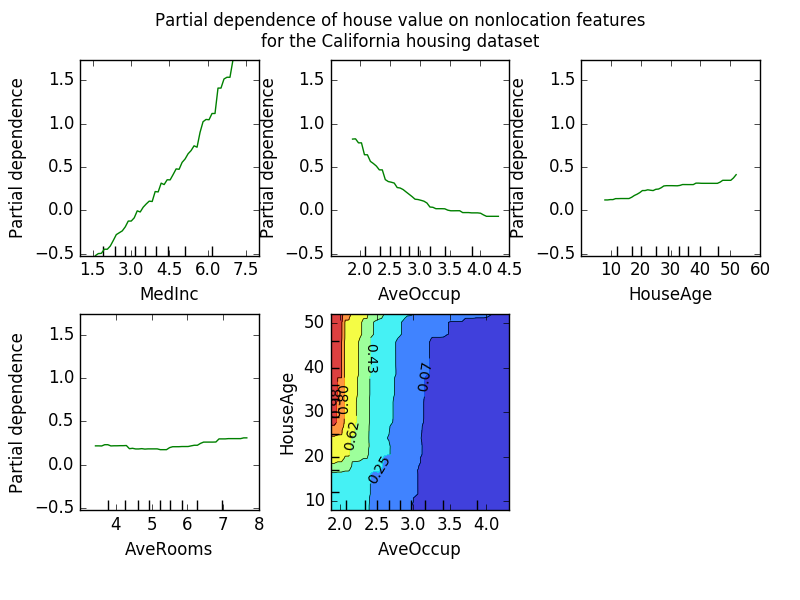
Einweg-PDP lehrt die Interaktion zwischen Zielantwort und Zielmerkmalen (z. B. linear, nicht linear). Die Darstellung oben links in der Abbildung oben zeigt die Auswirkung des Durchschnittseinkommens innerhalb eines Bezirks auf die mittleren Immobilienpreise. Wir können die lineare Beziehung zwischen ihnen klar erkennen. Ein PDP mit zwei Zielmerkmalen zeigt eine Interaktion zwischen den beiden Merkmalen. Zum Beispiel zeigt der PDP mit zwei Variablen in der obigen Abbildung, wie der mittlere Eigenheimpreis vom gemeinsamen Wert des Haushaltsalters und des Durchschnitts abhängt. Anzahl der Bewohner pro Haushalt. Sie können die Interaktion zwischen den beiden Funktionen deutlich sehen. Für zwei oder mehr Personen ist der Preis des Hauses fast unabhängig vom Alter des Hauses, während er für weniger als zwei Personen stark altersabhängig ist. Das Modul Partial_dependence ist eine praktische Funktion plot_partial_dependence, die unidirektionale und bidirektionale partielle Abhängigkeitsdiagramme erstellt. sklearn.ensemble.partial_dependence.plot_partial_dependence). Das folgende Beispiel zeigt, wie Sie ein Raster aus teilweise abhängigen Diagrammen erstellen. Zwei unidirektionale PDPs mit Merkmalsgrößen "0" und "1" und bidirektionalen PDPs zwischen den beiden Merkmalsgrößen.
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.ensemble.partial_dependence import plot_partial_dependence
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> fig, axs = plot_partial_dependence(clf, X, features)
Bei Modellen mit mehreren Klassen müssen Sie das Argument label verwenden, um die Klassenbezeichnung festzulegen, mit der der PDP erstellt wird.
>>>
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
... max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> fig, axs = plot_partial_dependence(mc_clf, X, features, label=0)
Wenn Sie den Rohwert einer teilweise abhängigen Funktion anstelle eines Diagramms möchten, wählen Sie partielle Abhängigkeit. Sie können die Funktion partielle_abhängigkeit (partielle Abhängigkeit) verwenden:
>>>
>>> from sklearn.ensemble.partial_dependence import partial_dependence
>>> pdp, axes = partial_dependence(clf, [0], X=X)
>>> pdp
array([[ 2.46643157, 2.46643157, ...
>>> axes
[array([-1.62497054, -1.59201391, ...
Die Funktion erfordert entweder das Argument "Gitter", das den Wert des Zielmerkmals angibt, für das die Teilabhängigkeitsfunktion ausgewertet werden soll, oder das Argument "X", das ein einfacher Modus zum automatischen Erstellen eines Gitters aus Trainingsdaten ist. Machen. Wenn "X" angegeben ist, ist der von der Funktion zurückgegebene Achsenwert die Achse für jede Zielmerkmalsmenge. Für jeden Wert des "Ziel" -Features im "Gitter" muss die teilweise abhängige Funktion die Vorhersage des Baums über alle möglichen Werte des "komplementären" Merkmals hinweg entfremden. Im Entscheidungsbaum kann diese Funktion ohne Bezugnahme auf Trainingsdaten effizient ausgewertet werden. Für jeden Gitterpunkt wird eine gewichtete Baumdurchquerung durchgeführt: Wenn der geteilte Knoten ein "Ziel" -Feature enthält, verzweigt er nach links oder rechts. Ansonsten folgen Sie beiden Zweigen. Jeder Zweig wird mit dem Prozentsatz der Trainingsmuster in diesem Zweig gewichtet. Schließlich ergibt sich die teilweise Abhängigkeit aus dem gewichteten Durchschnitt aller besuchten Riffe. Für Baumensembles werden die Ergebnisse für einzelne Bäume neu gemittelt.
-
Fußnote
-
[1] In der Klassifizierung Verlust = 'Abweichung' lautet die Zielantwort logit (p).
-
[2] Genauer gesagt die Erwartung der Zielantwort nach Berücksichtigung des ursprünglichen Modells. Das partielle Abhängigkeitsdiagramm enthält nicht das Init-Modell.
-
Beispiel:
-
Verweise
-
[F2001](1, 2, 3) J. Friedman, "Greedy Function Approximation: Gradient Boost Machine", Statistischer Jahresbericht, Bd. Band 29, Ausgabe 5, 2001.
-
[F1999] Friedman, "Probabilistic Gradient Boost", 1999
-
[HTF2009] Hastie, R. Tibshirani und J. Friedman, "Elements of Statistical Learning Ed. 2", Springer, 2009.
-
[R2007] Ridgeway, "Generalized Boosted Models: GBM Package Guide", 2007
1.11.5. VotingClassifier
Die Idee hinter der Implementierung des Abstimmungsklassifikators besteht darin, konzeptionell unterschiedliche Klassifikatoren für maschinelles Lernen zu kombinieren und Klassenbezeichnungen unter Verwendung der Mehrheitsabstimmung oder der durchschnittlichen Vorhersagewahrscheinlichkeit (weiche Abstimmung) vorherzusagen. Solche Klassifikatoren können in einer Reihe von Modellen nützlich sein, die auch gut funktionieren, um individuelle Schwächen auszugleichen.
1.11.5.1. Etiketten für die Mehrheit der Klassen (Mehrheit / sorgfältige Auswahl)
Bei einer Mehrheitsentscheidung ist das prädiktive Klassenlabel für eine bestimmte Stichprobe das Klassenlabel, das die Mehrheit (den Modus) des von den einzelnen Klassifikatoren vorhergesagten Klassenlabels darstellt.
Zum Beispiel die Vorhersage einer bestimmten Stichprobe
- Klassifikator 1 → Klasse 1
- Klassifikator 2 → Klasse 1
- Klassifikator 3 → Klasse 2
VotingClassifier (vote = 'hard') klassifiziert Samples basierend auf einer großen Anzahl von Klassenbezeichnungen als" Klasse 1 ".
Wenn sie gleich sind, wählt VotingClassifier die Klasse basierend auf der aufsteigenden Sortierreihenfolge aus. Zum Beispiel im folgenden Szenario
- Klassifikator 1 → Klasse 2
- Klassifikator 2 → Klasse 1
Das Klassenlabel 1 ist der Probe zugeordnet.
1.11.5.1.1. Verwendung
Das folgende Beispiel zeigt, wie ein Mehrheitsregelklassifizierer angepasst wird.
>>> from sklearn import datasets
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import VotingClassifier
>>> iris = datasets.load_iris()
>>> X, y = iris.data[:, 1:3], iris.target
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='hard')
>>> for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
... scores = cross_val_score(clf, X, y, cv=5, scoring='accuracy')
... print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
Accuracy: 0.90 (+/- 0.05) [Logistic Regression]
Accuracy: 0.93 (+/- 0.05) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [naive Bayes]
Accuracy: 0.95 (+/- 0.05) [Ensemble]
1.11.5.2. Gewichtete Durchschnittswahrscheinlichkeit (weiche Abstimmung)
Im Gegensatz zur Mehrheit der Stimmen (harte Stimmen) geben weiche Stimmen das Klassenlabel als Gesamtargmax der vorhergesagten Wahrscheinlichkeiten zurück.
Jedem Klassifikator können über den Parameter weight spezifische Gewichte zugewiesen werden. Angesichts der Gewichte werden die vorhergesagten Klassenwahrscheinlichkeiten für jeden Klassifikator gesammelt, die Klassifikatorgewichte multipliziert und gemittelt. Das endgültige Klassenlabel wird vom Klassenlabel mit der höchsten durchschnittlichen Wahrscheinlichkeit abgeleitet.
Um dies mit einem einfachen Beispiel zu erklären, nehmen wir an, dass es drei Klassifizierer gibt, "w1 = 1", "w2 = 1" und "w3 = 1", und drei Klassen von Klassifizierungsproblemen, die allen Klassifizierern gleiche Gewichte zuweisen. Ich werde.
Die gewichtete Durchschnittswahrscheinlichkeit der Stichprobe wird wie folgt berechnet:
| Sorter | Klasse 1 | Klasse 2 | Klasse 3 |
|---|---|---|---|
| Klassifikator 1 | w1 * 0.2 | w1 * 0.5 | w1 * 0.3 |
| Klassifikator 2 | w2 * 0.6 | w2 * 0.3 | w2 * 0.1 |
| Klassifikator 3 | w3 * 0.3 | w3 * 0.4 | w3 * 0.3 |
| gewichteter Durchschnitt | 0.37 | 0.4 | 0.23 |
Hier ist die prädiktive Klassenbezeichnung 2, da sie die höchste durchschnittliche Wahrscheinlichkeit aufweist. Das folgende Beispiel zeigt, wie sich der Entscheidungsbereich ändert, wenn der weiche VotingClassifier basierend auf einer linearen Unterstützungsvektormaschine, einem Entscheidungsbaum und einem Klassifikator in der Nähe von K verwendet wird.
>>> from sklearn import datasets
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> from sklearn.svm import SVC
>>> from itertools import product
>>> from sklearn.ensemble import VotingClassifier
>>> # Loading some example data
>>> iris = datasets.load_iris()
>>> X = iris.data[:, [0,2]]
>>> y = iris.target
>>> # Training classifiers
>>> clf1 = DecisionTreeClassifier(max_depth=4)
>>> clf2 = KNeighborsClassifier(n_neighbors=7)
>>> clf3 = SVC(kernel='rbf', probability=True)
>>> eclf = VotingClassifier(estimators=[('dt', clf1), ('knn', clf2), ('svc', clf3)], voting='soft', weights=[2,1,2])
>>> clf1 = clf1.fit(X,y)
>>> clf2 = clf2.fit(X,y)
>>> clf3 = clf3.fit(X,y)
>>> eclf = eclf.fit(X,y)
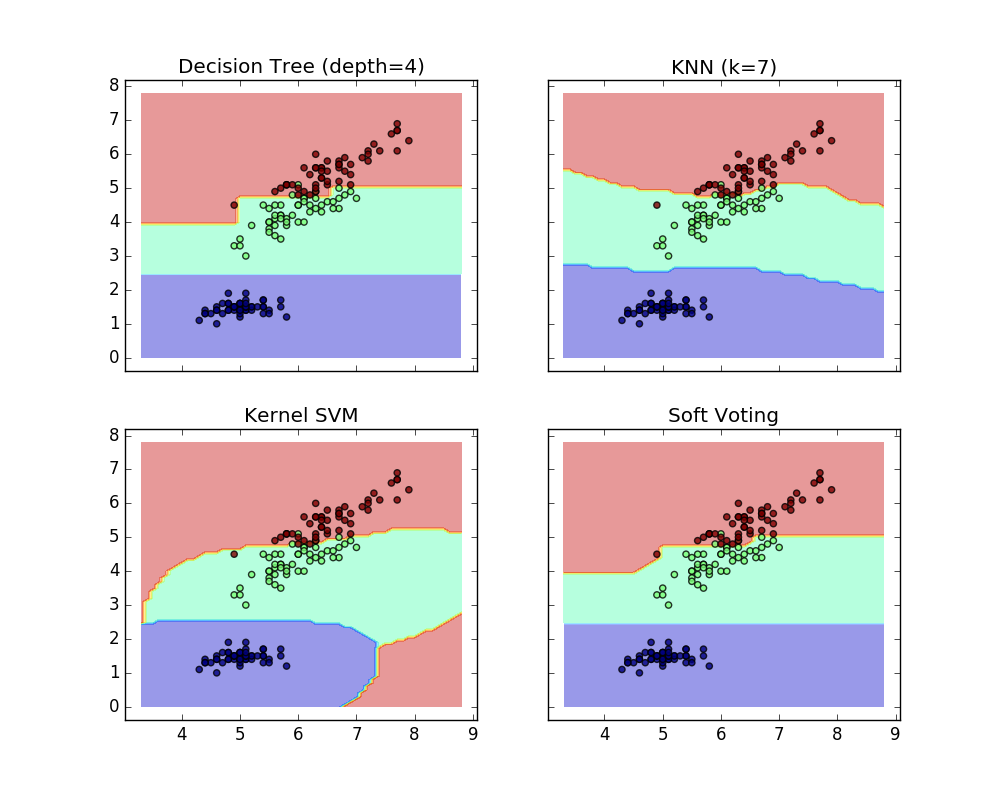
1.11.5.3. Verwenden des Abstimmungsklassifikators mit der Rastersuche
VotingClassifier kann auch mit GridSearch verwendet werden, um die Hyperparameter einzelner Schätzer anzupassen.
>>> from sklearn.model_selection import GridSearchCV
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft')
>>> params = {'lr__C': [1.0, 100.0], 'rf__n_estimators': [20, 200],}
>>> grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
>>> grid = grid.fit(iris.data, iris.target)
1.11.5.3.1 Verwendung
Um Klassenbezeichnungen basierend auf vorhergesagten Klassenwahrscheinlichkeiten vorherzusagen (VotingClassifier-Scikit-Lear-Schätzer müssen die Predict_Proba-Methode unterstützen)
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft')
Optional können Sie einzelne Klassifikatoren gewichten.
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft', weights=[2,5,1])
[scikit-learn 0.18 Benutzerhandbuch 1. Überwachtes Lernen](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98 Von% E3% 81% 8D% E5% AD% A6% E7% BF% 92)
© 2010 - 2016, Entwickler von Scikit-Learn (BSD-Lizenz).