google übersetzte http://scikit-learn.org/0.18/modules/outlier_detection.html [scikit-learn 0.18 Benutzerhandbuch 2. Lernen ohne Lehrer](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA Von% E3% 81% 97% E5% AD% A6% E7% BF% 92)

2.7 Erkennung von Neuheiten und Ausreißern

Viele Anwendungen müssen feststellen können, ob eine neue Beobachtung zur gleichen Verteilung (Inlier) gehört wie eine vorhandene Beobachtung oder ob es sich um eine andere handelt (Ausreißer). Diese Funktion wird häufig verwendet, um den tatsächlichen Datensatz zu löschen. Es müssen zwei wichtige Unterscheidungen getroffen werden:

** Neuheitserkennung: **
Trainingsdaten werden nicht von Ausreißern verschmutzt, daher bin ich daran interessiert, Anomalien mit neuen Beobachtungen zu erkennen.
** Ausreißererkennung: **
Die Trainingsdaten enthalten Ausreißer und sollten an den zentralen Modus der Trainingsdaten angepasst werden, wobei die Abweichungsbeobachtungen ignoriert werden.

Das Scikit-Learn-Projekt bietet eine Reihe von Tools für maschinelles Lernen, die sowohl zur Erkennung von Neuheiten als auch zur Erkennung von Ausreißern verwendet werden können. Diese Strategie wird mit Objekten implementiert, die unbeaufsichtigt aus den Daten lernen.

estimator.fit(X_train)

Neue Beobachtungen können mithilfe von Vorhersagemethoden als Ausreißer oder Ausreißer sortiert werden.

estimator.predict(X_train)

Der Ausreißer ist mit 1 und der Ausreißer mit -1 gekennzeichnet.

2.7.1. Erkennung von Neuheiten

Betrachten Sie einen Datensatz mit $ n $ Beobachtungen mit derselben Verteilung, die durch $ p $ -Funktionen beschrieben wird. Erwägen Sie nun, diesem Datensatz eine weitere Beobachtung hinzuzufügen. Unterscheiden sich die neuen Beobachtungen so sehr von anderen Beobachtungen? (Dh, kommt es aus derselben Verteilung?) Oder ist es umgekehrt anderen so ähnlich, dass es von der ursprünglichen Beobachtung nicht zu unterscheiden ist? Dies ist ein Problem, das durch Tools und Methoden zur Erkennung von Neuheiten behoben wird. Im Allgemeinen wird versucht, die groben, engen Grenzen zu lernen, die die anfängliche Beobachtungsverteilung umreißen, die durch Einbetten des $ p $ -Dimensionsraums dargestellt wird. Wenn sich dann weitere Beobachtungen innerhalb des durch Grenzen begrenzten Unterraums befinden, wird davon ausgegangen, dass sie aus derselben Population stammen wie die erste Beobachtung. Andernfalls können wir, wenn sie außerhalb der Grenze liegen, sagen, dass sie mit einem gewissen Vertrauen in unsere Einschätzung anomal sind. Ein-Klassen-SVM wurde von Schölkopf et al. Zu diesem Zweck die Support Vector Machines des Objekts svm.OneClassSVM (http://scikit-learn.org/0.18/modules/generated/sklearn.svm.OneClassSVM.html#sklearn.svm.OneClassSVM). http://qiita.com/nazoking@github/items/2b16be7f7eac940f2e6a) Es ist im Modul implementiert. Um die Grenze zu definieren, müssen Sie die Kernel- und Skalarparameter auswählen. RBF-Kernel haben normalerweise keine genaue Formel oder keinen Algorithmus zum Festlegen von Bandbreitenparametern, aber sie werden ausgewählt. Dies ist die Standardeinstellung für die Implementierung von scicit-learn. Der Parameter $ \ nu $, auch als One-Class-SVM-Marge bekannt, entspricht der Wahrscheinlichkeit, neue, aber regelmäßige Beobachtungen außerhalb der Grenze zu finden.

Verweise:
Schätzung der Unterstützung für eine hochdimensionale Verteilung Schölkopf, Bernhard et al. Neural Computing 13.7 (2001): 1443 & ndash; 1471.
Beispiel:
svm.OneClassSVM Die Grenze lernte einige Daten des Objekts Zur Visualisierung 1 Klasse SVM mit nichtlinearem Kernel (RBF) Siehe -oneclass-py).

2.7.2 Ausreißererkennung

Die Off-Value-Erkennung ähnelt der Neuheitserkennung, da sie den Kern normaler Beobachtungen von kontaminiertem Material ("Ausreißer" genannt) trennt. Im Fall der Ausreißererkennung verfügen wir jedoch nicht über einen sauberen Datensatz, der eine Population regelmäßiger Beobachtungen darstellt, mit denen ein beliebiges Werkzeug trainiert werden kann.

2.7.2.1 Installieren Sie den ovalen Umschlag

Eine übliche Methode zur Durchführung einer Ausreißererkennung besteht darin, anzunehmen, dass normale Daten aus einer bekannten Verteilung stammen (z. B. sind die Daten eine Gaußsche Verteilung). Ausgehend von dieser Annahme versuchen wir im Allgemeinen, die "Form" der Daten zu definieren, und der Abweichungswert kann als Beobachtungswert definiert werden, der weit von der Anpassungsform entfernt ist. scikit-learn ermöglicht die gemeinsame Verteilung von Objekten. Die elliptische Hüllkurve passt eine robuste Kovarianzschätzung an die Daten an und passt die Ellipse an den zentralen Datenpunkt an, wobei andere Punkte als der zentrale Modus ignoriert werden. Angenommen, die Inlier-Daten sind Gaußsch, werden die Inlier-Position und die Kovarianz auf robuste Weise geschätzt (dh vom Ausreißer nicht beeinflusst). Der aus dieser Schätzung erhaltene Maharanobis-Abstand wird verwendet, um ein Maß für die Exogenität abzuleiten. Diese Strategie wird unten gezeigt.

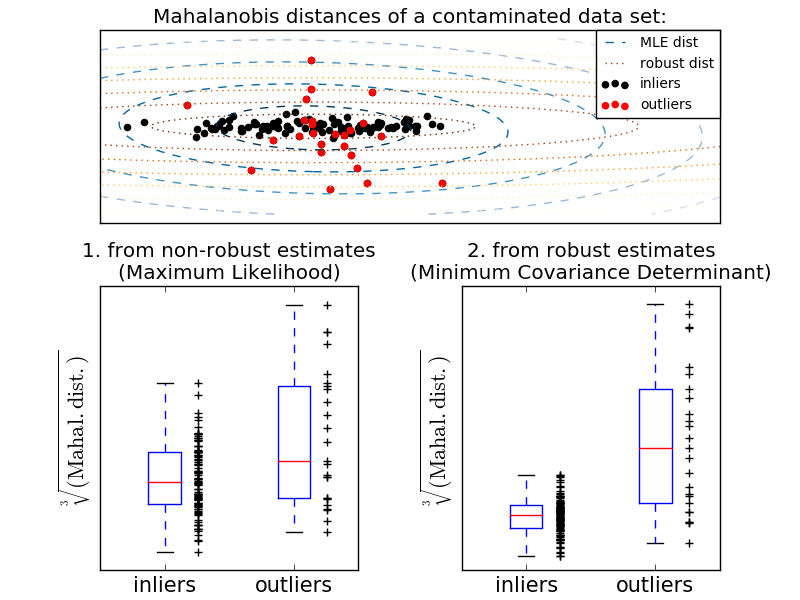
Beispiel:
Standard (covariance.EmpiricalCovariance) zur Bewertung des Grads der Abweichung von der Beobachtung ) Oder die Verwendung robuster Schätzungen (covariance.MinCovDet) Informationen zum Unterschied finden Sie unter [Beziehung zwischen robuster Kovarianzschätzung und Maharanobis-Entfernung](http://scikit-learn.org/0.18/auto_examples/covariance/plot_mahalanobis_distances.html#sphx-glr-auto-examples-covariance- Siehe Handlung-Mahalanobis-Entfernungen-py).
Verweise:
[RD1999] Rousseeuw, P. J., Van Driessen, K. "Schnelle Algorithmen für minimale Kovarianzmatrixschätzer" Technometrics 41 (3), 212 (1999)

2.7.2.2 Isolationswald

Eine effiziente Methode zum Erkennen von Ausreißern in hochdimensionalen Datensätzen ist die Verwendung einer zufälligen Gesamtstruktur. ensemble.IsolationForest wählt zufällig Features aus und maximiert die ausgewählten Features. "Trennen" Sie Beobachtungen, indem Sie zufällig eine Aufteilung zwischen dem Wert und dem Minimum auswählen. Rekursive Teilungen können in einer Baumstruktur dargestellt werden, sodass die Anzahl der Teilungen, die zum Trennen eines Samples erforderlich sind, der Pfadlänge vom Wurzelknoten zum Endknoten entspricht. Die Länge eines Pfades, gemittelt über einen solchen zufälligen Baumwald, ist ein Maß für Normalität und Urteilsvermögen. Die zufällige Teilung führt zu einem deutlich kürzeren Pfad für Anomalien. Wenn eine zufällige Baumstruktur generisch kürzere Pfadlängen für eine bestimmte Stichprobe erzeugt, sind diese wahrscheinlich anomal. Diese Strategie wird unten gezeigt.

Beispiel:
Beispiele für die Verwendung von IsolationForest finden Sie unter Beispiele für IsolationForest (http://scikit-learn.org/0.18/auto_examples/ensemble/plot_isolation_forest.html#sphx-glr-auto-examples-ensemble-plot-isolation-forest- Siehe py).
Ausreißererkennung mit verschiedenen Methoden Bitte beziehen Sie sich auf. ensemble.IsolationForest und [svm.OneClassSVM](http: // scikit-learn) .org / 0.18 / modules / generate / sklearn.svm.OneClassSVM.html # sklearn.svm.OneClassSVM) (auf Ausreißererkennungsmethode abgestimmt) und [covariance.MinCovDet](http: // scikit- Vergleichen Sie die kovarianzbasierte Ausreißererkennung mit learn.org/0.18/modules/generated/sklearn.covariance.MinCovDet.html#sklearn.covariance.MinCovDet).
Verweise:
[LTZ2008] Liu, Fei Tony, Ting, Kai Ming, Zhou, Zhi-Hua. Data Mining "Separated Forest", 2008. ICDM '08. 8. Internationale IEEE-Konferenz

2.7.2.3. 1 Klasse SVM gegen elliptische Hülle gegen Isolationswald

Genau genommen ist eine SVM der Klasse 1 eine neue Erkennungsmethode, keine Ausreißererkennungsmethode: Der Trainingssatz sollte nicht kontaminiert sein, da er von den Ausreißern angepasst wird. Kurz gesagt, es ist sehr schwierig, Ausreißer in höheren Dimensionen zu erkennen oder keine Annahmen über die Verteilung der zugrunde liegenden Daten zu treffen, und SVMs der Klasse 1 liefern in diesen Situationen nützliche Ergebnisse. Das folgende Beispiel zeigt, wie sich die gemeinsam verteilte Leistung mit weniger Daten und weniger verschlechtert.

svm.OneClassSVM funktioniert gut mit Daten mit mehreren Modi und Ensembles. IsolationForest funktioniert in allen Fällen gut.

Vergleich des 1-Klassen-SVM-Ansatzes und der elliptischen Hüllkurve

Für einen gut zentrierten ovalen Inlier-Modus svm.OneClassSVM Sie können nicht von der Rotationssymmetrie der früheren Population profitieren. Darüber hinaus passt es leicht in die Ausreißer des Trainingssatzes. Umgekehrt ist covariance.EllipticEnvelope basierend auf der Anpassung der Kovarianz eine frühere Verteilung. Lernen Sie eine Ellipse, die sehr ähnlich aussieht. ensemble.IsolationForest funktioniert ebenfalls.

Elliptic Envelope passt nicht gut zu Lieferanten, wenn die Inlier-Verteilung bimodal wird. Covariance.EllipticEnvelope und [svm.OneClassSVM](http: // scit) -Learn.org/0.18/modules/generated/sklearn.svm.OneClassSVM.html#sklearn.svm.OneClassSVM) Beide haben Schwierigkeiten, die beiden Modi [svm.OneClassSVM](http: // scikit) zu erkennen. Sie können sehen, dass -learn.org/0.18/modules/generated/sklearn.svm.OneClassSVM.html#sklearn.svm.OneClassSVM) dazu neigt, zu überschreiben. Da es kein Modell für Lieferanten gibt, wird der Bereich, in dem einige Ausreißer gruppiert sind, als Inlier interpretiert.

Wenn die Inlier-Verteilung stark und nicht Gaußsch ist, ist svm.OneClassSVM [ensemble.IsolationForest] ](Http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.IsolationForest.html#sklearn.ensemble.IsolationForest) kann eine vernünftige Annäherung wiederherstellen, aber covariance.EllipticEnvelope schlägt vollständig fehl.

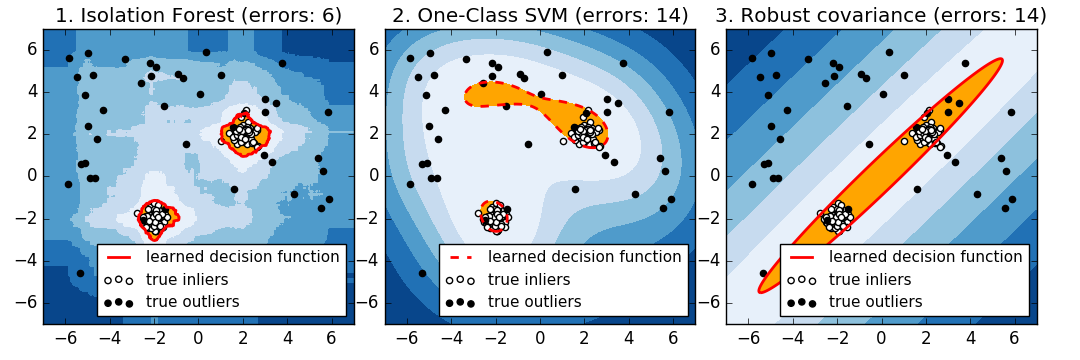
Beispiel:
Beispiele für die Verwendung von IsolationForest finden Sie unter Beispiele für IsolationForest (http://scikit-learn.org/0.18/auto_examples/ensemble/plot_isolation_forest.html#sphx-glr-auto-examples-ensemble-plot-isolation-forest- Siehe py).
Ausreißererkennung mit verschiedenen Methoden Bitte beziehen Sie sich auf. ensemble.IsolationForest und [svm.OneClassSVM](http: // scikit-learn) .org / 0.18 / modules / generate / sklearn.svm.OneClassSVM.html # sklearn.svm.OneClassSVM) (auf Ausreißererkennungsmethode abgestimmt) und [covariance.MinCovDet](http: // scikit- Vergleichen Sie die kovarianzbasierte Ausreißererkennung mit learn.org/0.18/modules/generated/sklearn.covariance.MinCovDet.html#sklearn.covariance.MinCovDet).

[scikit-learn 0.18 Benutzerhandbuch 2. Lernen ohne Lehrer](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA Von% E3% 81% 97% E5% AD% A6% E7% BF% 92)

[PYTHON] [Übersetzung] scikit-learn 0.18 Benutzerhandbuch 2.7. Erkennung von Neuheiten und Ausreißern