Beispiel für eine Problemeinstellung

Beispiel 1) Lösen Sie die Laplace-Gleichung. Wie in der Figur gezeigt, ist die Randbedingung \ phi = V Volt bei y = 0. Es ist an anderen Grenzen geerdet und beträgt 0 Volt. Die elektrostatische Position zu diesem Zeitpunkt wird bestimmt und visualisiert.

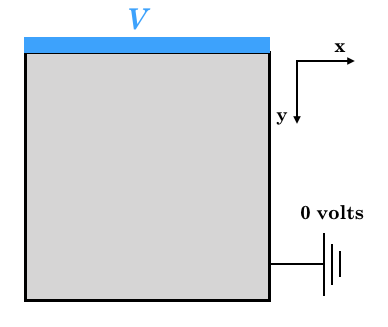
Beispiel (2) Lösen Sie die Poisson-Gleichung. Stellen Sie die externe Ladung Q in den in Beispiel (1) betrachteten Bereich. Zu diesem Zeitpunkt werden die elektrostatische Position $ \ phi $ und das elektrische Feld $ E = - \ nabla \ phi $ erhalten und visualisiert.

Beispiel (1) Poisson-Gleichung

Animation wird auch im Code generiert. Hier soll untersucht werden, wie die Lösung \ phi (x, y) konvergiert.

Nachtrag 17. Dezember 2017: Es wird angenommen, dass es auf Jupyter funktioniert. Wenn Sie jupyter nicht verwenden, kommentieren Sie "% matplotlib nbagg" in Ihrem Code aus. Aus der Sicht von masa_stone22.

laplace.py3

"""
Laplace-Gleichung:Numerische Lösung,Jacobi(Jacobi)Recht: 
12 Aug. 2017
"""
%matplotlib nbagg 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation #Importieren Sie Methoden zum Erstellen von Animationen

fig = plt.figure()
anim = [] 

# 
delta_L=0.1  #Gitterbreite
LL = 10 #Quadratische Breite
L = int(LL/delta_L)

V = 5.0 #Einseitiges Grenzpotential
convegence_criterion = 10**-3  #Konvergenzbedingung. Wenn Sie die Genauigkeit verbessern möchten, verringern Sie diesen Wert.

phi = np.zeros([L+1,L+1])
phi[0,:] = V #Randbedingung
phi2 = np.empty ([L+1,L+1])

#for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])

    
#Maine
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
    if n_iter % 100 ==0:  #Überwachung des Konvergenzstatus
        print("iteration No =", n_iter, "delta=",delta)
    conv_check.append([n_iter, delta])
    for i in range(L+1):
        for j in range(L+1):
            if i ==0 or i ==L or j==0 or j==L:
                phi2[i,j] = phi[i,j]
            else: 
                phi2[i,j] = (phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4 #Nachtrag:Formel(11)Sehen
    delta = np.max(abs(phi-phi2))

    phi, phi2 = phi2, phi
    n_iter+=1
    
    im=plt.imshow(phi,cmap='hsv')
    anim.append([im])

#for plot        
plt.colorbar () #Farbbalkenanzeige
plt.xlabel('X')
plt.ylabel('Y')
ani = ArtistAnimation(fig, anim, interval=100, blit=True,repeat_delay=1000)
ani.save("t.gif", writer='imagemagick')  
plt.show()

Ergebnis (1) Lösung der Laplace-Gleichung

Die Randbedingung $ \ phi = 5 $ von y = 0 ist erfüllt. Die Potentialänderung ist nahe der Grenze groß.

Beispiel (2) Lösung der Poisson-Gleichung, wenn eine externe Ladung eingebettet ist

Die externe Ladungsdichte betrug $ c = 1000 $ und das Grenzpotential betrug $ V = 5 $.

Poisson.py3

"""
Poisson-Gleichung:Jacobi(Jacobi)Recht
Zeigt auch das elektrische Feld an: 
12 Aug. 2017
"""
%matplotlib nbagg 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation #Importieren Sie Methoden zum Erstellen von Animationen

anim = [] 

# 
delta_L=0.01 #Gitterbreite
LL = 1 #Quadratische Breite
L = int(LL/delta_L)

V = 5.0 #Grenze y=0 Potential(Randbedingung)
convegence_criterion = 10**-5

phi = np.zeros([L+1,L+1])
phi[0,:] = V #Randbedingung
phi2 = np.empty ([L+1,L+1])

#Ladungsdichteeinstellung
eps0=1
charge= np.zeros([L+1,L+1])
c=1000 #Ladungsdichte

CC=int(L/4)
CC2=int(L/2)

#Ladungsdichte x=[L/4, L/2], y=[L/4,L/2]Im Bereich von einbetten
for i in range(CC, CC2+1):
    for j in range(CC,CC2+1):
        charge[i,j] = c
#

#for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])

    
#Maine
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
    if n_iter % 100 ==0:  #Überwachung des Konvergenzstatus
        print("iteration No =", n_iter, "delta=",delta)
    conv_check.append([n_iter, delta])
    for i in range(L+1):
        for j in range(L+1):
            if i ==0 or i ==L or j==0 or j==L:
                phi2[i,j] = phi[i,j]
            else: 
                phi2[i,j] = (phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4 + (delta_L**2/(4*eps0))*charge[i,j]
    delta = np.max(abs(phi-phi2))

    phi, phi2 = phi2, phi
    n_iter+=1
    
    im=plt.imshow(phi,cmap='hsv')
    anim.append([im])

    
#for plot    

pp=plt.colorbar (orientation="vertical") #Farbbalkenanzeige
pp.set_label("phi", fontname="Ariel", fontsize=24)
plt.xlabel('X',fontname="Ariel", fontsize=24)
plt.ylabel('Y',fontname="Ariel", fontsize=24)
plt.title('Solution of the Poisson equation for electrostatic potential ')
#ani = ArtistAnimation(fig, anim, interval=10, blit=True,repeat_delay=1000)
#ani.save("t.gif", writer='imagemagick')  

plt.show()



#Berechnung des elektrischen Feldes
Ex = np.zeros([L,L])
Ey = np.zeros([L,L])

for i in range(L):
    for j in range(L):
        Ex[i,j] = -(phi[i+1,j]-phi[i,j])/delta_L
        Ey[i,j] = -(phi[i,j+1]-phi[i,j])/delta_L

plt.figure()
        
X, Y= np.meshgrid(np.arange(0, L,1), np.arange(0, L,1))  #Netzgenerierung
plt.quiver(X,Y,Ex,Ey,color='red',angles='xy',scale_units='xy', scale=40) #Plotvektorfeld

plt.xlim([0,L]) #Bereich von X zum Zeichnen
plt.ylim([0,L]) #Bereich von y zum Zeichnen

#Diagrammzeichnung
plt.grid()
plt.draw()
plt.show()

Ergebnis (2): Lösung der Poisson-Gleichung für ein System mit eingebetteten externen Ladungen

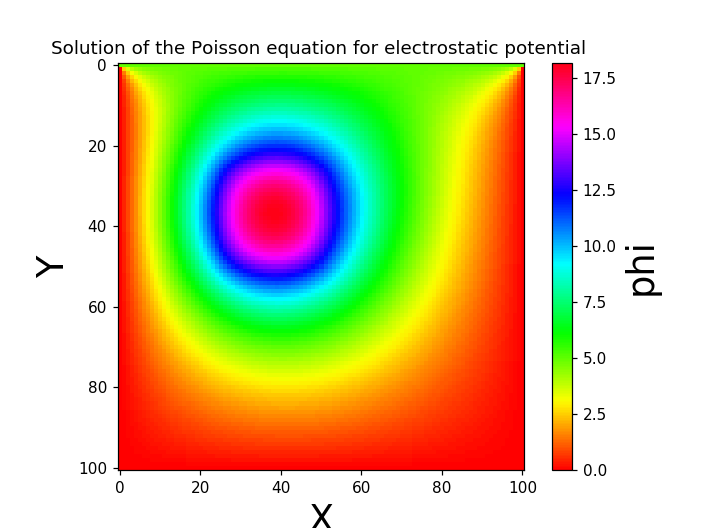
Die Randbedingung bei y = 0 ist $ \ phi = 5 $. Aufgrund der eingebetteten externen Ladung unterscheidet sich das Potential stark von Beispiel (1).

Der Zustand des elektrischen Feldes. (Die # y-Achse wurde umgekehrt). Diese Figur wurde als "Delta_L = 0,1" gezeichnet. Wie von der Schwankung des Potentials erwartet, schwankt das elektrische Feld in der Nähe der externen Ladung stark.

Nachtrag

Nachtrag (1): Theorie

Der relationale Ausdruck zwischen dem elektrostatischen Feld $ E $ und dem Potential $ \ phi $ E = - \nabla \phi \tag{1} Und Gaußsches Gesetz zwischen den Ladungsdichten $ \ rho $ und $ E $

\nabla \cdot E =\frac{\rho} {\epsilon_0} \tag{2}

Ist der Ausgangspunkt.

Einsetzen von (1) in (2)

\Delta \phi (x,y,z) =-\frac{\rho (x,y,z)} {\epsilon_0} \tag{3}

Bekommen. Dies ist die Poisson-Gleichung. Wobei $ \ epsilon_0 $ die Dielektrizitätskonstante im Vakuum ist.

Wenn es überall im Raum keine wahre Ladung gibt ($ \ rho (x, y, z) = 0 $), ist die Poisson-Gleichung

\Delta \phi (x,y,z) =0 \tag{4} Wird sein. Dies ist die Laplace-Gleichung.

Nachtrag (2): Numerische Lösung: Jacobi-Methode

Denken Sie an zwei Dimensionen. Poisson-Gleichung

$ \frac{\partial^2 \phi(x,y)}{\partial x^2} + \frac{\partial^2 \phi(x,y)}{\partial y^2} =-\frac{\rho (x,y,z)} {\epsilon_0} \tag{5}$

Wird sein. Stellen Sie sich ein zweidimensionales Gitter (siehe Abbildung unten) vor, das durch eine Breite von $ \ Delta $ in den Richtungen $ x $ und $ y $ getrennt ist. Wenn das Potential $ \ phi (x, y) $ von Taylor an dem Punkt ($ x + \ Delta, y $) erweitert wird,

\phi(x+\Delta,y)=\phi(x,y)+\frac{\partial \phi}{\partial x}\Delta +\frac{1}{2}\frac{\partial^2 \phi}{\partial x^2}\Delta^2 + \frac{1}{6}\frac{\partial^3 \phi}{\partial x^3}\Delta^3+\frac{1}{24}\frac{\partial^4 \phi}{\partial x^4}\Delta^4 + \mathcal{O}(\Delta^5) \tag{6}

\phi(x-\Delta,y)=\phi(x,y)-\frac{\partial \phi}{\partial x}\Delta +\frac{1}{2}\frac{\partial^2 \phi}{\partial x^2}\Delta^2 - \frac{1}{6}\frac{\partial^3 \phi}{\partial x^3}\Delta^3+\frac{1}{24}\frac{\partial^4 \phi}{\partial x^4}\Delta^4 + \mathcal{O}(\Delta^5) \tag{7}

Wenn die Gleichungen (6) und die Gleichung (7) addiert werden,

$\frac{\partial^2 \phi(x,y)}{\partial x^2} = \frac{\phi(x+\Delta,y)+ \phi(x-\Delta,y)-2\phi(x,y)}{\Delta^2} +\mathcal{O}(\Delta^2) \tag{8} $

Führen Sie die Taylor-Erweiterung für y auf die gleiche Weise durch: $\frac{\partial^2 \phi(x,y)}{\partial y^2} = \frac{\phi(x,y+\Delta)+ \phi(x,y-\Delta)-2\phi(x,y)}{\Delta^2} +\mathcal{O}(\Delta^2) \tag{9} $

Bekommen. Ersetzen Sie die Gleichungen (8) und (9) durch (5) und sortieren Sie sie ein wenig aus.

$ \phi(x,y) = \frac{1}{4} [\phi(x+\Delta,y)+\phi(x-\Delta,y)+\phi(x,y+\Delta)+\phi(x,y-\Delta)]+\frac{\rho(x,y)}{4 \epsilon_0}\Delta^2+\mathcal{O}(\Delta^4) \tag{10} $

Bekommen. Dies ist eine ** Differentialdarstellung der Poisson-Gleichung **. Der Fehler ist $ \ mathcal {O} (\ Delta ^ 4) $.

Wenn $ \ rho (x, y) = 0 $

$\phi(x,y) = \frac{1}{4} [\phi(x+\Delta,y)+\phi(x-\Delta,y)+\phi(x,y+\Delta)+\phi(x,y-\Delta)]+\mathcal{O}(\Delta^4) \tag{11} $

Wird sein. Dies ist eine ** Differentialdarstellung der Laplace-Gleichung **.

Wenn bei der numerischen Berechnung der Index des Arrays $ (x_i, y_j) $ ist, ist Gleichung (10)

$ \phi(x_i,y_j) = \frac{1}{4} [\phi(x_{i+1},y_{j})+\phi(x_{i-1},y_{j})+\phi(x_{i},y_{j+1})+\phi(x_{i},y_{j-1})]+\frac{\rho(x_{i},y_{j})}{4\epsilon_0}\Delta^2　\tag{12} $ Wird sein.

Das Potential $ \ phi (i, j) $ am Punkt $ (x_i, y_j) $ wird angenähert, indem der zur Ladungsdichte $ \ rho (x, y) $ proportionale Betrag zum Durchschnittswert der Werte der umgebenden vier Punkte addiert wird. Ist fertig (siehe Abbildung unten).

** Geben Sie zunächst die Randbedingung und den geschätzten Wert des Potentials in der Region an, lösen Sie Gleichung (12) in allen Regionen und wiederholen Sie den Vorgang, bis die Lösung in der Region konvergiert. Dies ist die Jacobi-Methode. ** Die Anzahl der sich wiederholenden Konvergenzschritte ist ungefähr proportional zum Quadrat der Anzahl der Datenpunkte [1].

Diese Methode ist sehr langsam konvergierend und unpraktisch, bietet jedoch eine Grundlage für das Verständnis moderner Methoden.

Verweise

Die Jacobi-Methode und eine leicht modifizierte gute Berechnungsmethode [Gauß-Seidel-Methode](https://ja.wikipedia.org/wiki/%E3%82%AC%E3%82%A6%E3%82% B9% EF% BC% 9D% E3% 82% B6% E3% 82% A4% E3% 83% 87% E3% 83% AB% E6% B3% 95) ist langsam und unpraktisch. Schnellere Schemata umfassen die sequentielle Überminderungsmethode (SOR-Methode) (https://ja.wikipedia.org/wiki/SOR%E6%B3%95) [1,2].

[1] ["Numerisches Rezept in der japanischen Seeversion - Rezept für die numerische Berechnung in C-Sprache"](https://www.amazon.co.jp/%E3%83%8B%E3%83%A5 % E3% 83% BC% E3% 83% A1% E3% 83% AA% E3% 82% AB% E3% 83% AB% E3% 83% AC% E3% 82% B7% E3% 83% 94-% E3% 82% A4% E3% 83% B3-% E3% 82% B7% E3% 83% BC-% E6% 97% A5% E6% 9C% AC% E8% AA% 9E% E7% 89% 88- C% E8% A8% 80% E8% AA% 9E% E3% 81% AB% E3% 82% 88% E3% 82% 8B% E6% 95% B0% E5% 80% A4% E8% A8% 88% E7% AE% 97% E3% 81% AE% E3% 83% AC% E3% 82% B7% E3% 83% 94-Press-William-H / dp / 4874085601 / ref = dp_return_1? _ Codierung = UTF8 & n = 465392 & s = Bücher) Technical Review, 1993.

Als etwas, das im Netz angesehen werden kann

http://www.na.scitec.kobe-u.ac.jp/~yamamoto/lectures/appliedmathematics2006/chapter8.PDF

Wann

http://web.econ.keio.ac.jp/staff/ito/pdf02/pde2.pdf

Ich werde auflisten.

Nachtrag: 14. August 2017

Ich habe einen Artikel über die SOR-Methode und die Gauß-Seidel-Methode veröffentlicht.

[2] Qiita-Artikel, [[Wissenschaftlich-technische Berechnung von Python] Vergleich der Konvergenzgeschwindigkeiten der Jacobi-Methode / Gauß-Seidel-Methode / SOR-Methode für Laplace-Gleichung, partielle Differentialgleichung, Randwertproblem, numerische Berechnung](http: // qiita.com/sci_Haru/items/b98791f232b93690a6c3)

Nachtrag: ** Code zur Lösung der Poisson-Gleichung nach der SOR-Methode **

Der Code zum Lösen der Poisson-Gleichung in Beispiel (2) durch die in Artikel [2] erläuterte SOR-Methode wird veröffentlicht. Es konvergiert mehr als zehnmal schneller als die Jakobi-Methode </ font>. Verwenden Sie diese Option.

"""
Poisson-Gleichung:Numerische Lösung,SOR-Methode
Zeigt auch das elektrische Feld an:
14 Aug. 2017
"""
%matplotlib nbagg 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation #Importieren Sie Methoden zum Erstellen von Animationen
import matplotlib.animation as animation


anim = [] 

# 
delta_Lx=0.01
delta_Ly=0.01
LLx = 1 #Quadratische Breite
LLy= 1

Lx = int(LLx/delta_Lx)
Ly = int(LLy/delta_Ly)



V = 5.0 #Stromspannung
convegence_criterion = 10**-5

phi = np.zeros([Lx+1,Ly+1])
phi_Bound= np.zeros([Lx+1,Ly+1])
phi_Bound[0,:] = V #Randbedingung

#Ladungsdichteeinstellung
eps0=1
charge= np.zeros([Lx+1,Ly+1])
c=1000

CC=int(Lx/4)
CC2=int(Ly/2)

for i in range(CC, CC2+1):
    for j in range(CC,CC2+1):
        charge[i,j] = c
#


# for SOR method
aa_recta=0.5*(np.cos(np.pi/Lx)+np.cos(np.pi/Ly))
omega_SOR_recta = 2/(1+np.sqrt(1-aa_recta**2)) #Beschleunigungsparameter in der SOR-Methode
print("omega_SOR_rect=",omega_SOR_recta)



#for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])

    
#Maine
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
    phi_in=phi.copy()
    if n_iter % 100 ==0:  #Überwachung des Konvergenzstatus
        print("iteration No =", n_iter, "delta=",delta)
    conv_check.append([n_iter, delta])
    for i in range(Lx+1):
        for j in range(Ly+1):
            if i ==0 or i ==Lx or j==0 or j==Ly:
                phi[i,j] = phi_Bound[i,j]
            else: 
                phi[i,j] = phi[i,j]+omega_SOR_recta *((phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4-phi[i,j]+ (delta_Lx*delta_Ly/(4*eps0))*charge[i,j]) # SOR =Gauß-Seidel+ OR
    delta = np.max(abs(phi-phi_in))


    n_iter+=1
    
    im=plt.imshow(phi,cmap='hsv')
    anim.append([im])

    
#for plot    

pp=plt.colorbar (orientation="vertical") #Farbbalkenanzeige
pp.set_label("phi", fontname="Ariel", fontsize=24)
plt.xlabel('X',fontname="Ariel", fontsize=24)
plt.ylabel('Y',fontname="Ariel",  fontsize=24)
plt.title('Solution of the Poisson equation for electrostatic potential ')
#ani = ArtistAnimation(fig, anim, interval=10, blit=True,repeat_delay=1000)
#ani.save("t.gif", writer='imagemagick')  

plt.show()



#Berechnung des elektrischen Feldes
Ex = np.zeros([Lx,Ly])
Ey = np.zeros([Lx,Ly])

for i in range(Lx):
    for j in range(Ly):
        Ex[i,j] = -(phi[i+1,j]-phi[i,j])/delta_Lx
        Ey[i,j] = -(phi[i,j+1]-phi[i,j])/delta_Ly

plt.figure()

X, Y= np.meshgrid(np.arange(0, Lx,1), np.arange(0, Ly,1))  #Netzgenerierung
plt.quiver(X,Y,Ex,Ey,color='red',angles='xy',scale_units='xy', scale=40) #Plotvektorfeld

plt.xlim([0,Lx]) #Bereich von X zum Zeichnen
plt.ylim([0,Ly]) #Bereich von y zum Zeichnen

#Diagrammzeichnung
plt.grid()
plt.draw()
plt.show()