[PYTHON] Genießen Sie Coursera / Machine Learning-Materialien zweimal
In letzter Zeit nehme ich Courseras Maechine Learning (Stanford University, von Andrew Ng). Natürlich ist das Erklärungsvideo auch nützlich, aber was diesen Kurs so gut macht, ist die Programmieraufgabe, die jedes Mal gegeben wird. Es ist nur Matlab-Code, daher wollte ich ihn in Python umschreiben, damit ich ihn später überprüfen kann. (Andere Leute können Beispiele für die gleichen Bemühungen im Internet sehen.)
Hier werde ich vorstellen, wie Sie die Unterrichtsmaterialien von "Coursera / Maschinelles Lernen" zwei- oder dreimal (in Python) genießen können. Wir erklären auch ** scipy.optimize.minimize () **, das zur Funktionsminimierung verwendet wird.
Kostenfunktion und deren Ableitung
Viele Materialien für maschinelles Lernen erstellen eine Kostenfunktion und suchen nach Parametern, die diese minimieren. Matlab verwendet fminunc () (oder fmincg (), das in der Task bereitgestellt wird), aber in Python unterstützt ** scipy.optimize.minimize () ** eine ähnliche Funktion.
Bereiten Sie zunächst die Kostenfunktion und ihre Ableitung selbst vor. In der ersten Aufgabe, dem linearen Modell, ist es durch die folgende Gleichung gegeben.
J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_{\theta}(x ^{(i)} ) -y ^{(i)}) ^2
\\
\frac{\partial J}{\partial \theta _j} = \frac{1}{m} \sum_{i=1}^{m}
(h_{\theta} (x^{(i)}) - y^{(i)} )x_j^{(i)}
$ h_ {\ theta} $ ist die Funktion, die bei der Modellierung angenommen wird. (Diesmal wird ein lineares Modell angenommen.)
def compute_cost(theta, xmat, ymat):
m = len(ymat)
one_v = np.ones(len(xmat))
xmat1 = np.column_stack((one_v, xmat)) # shape: m x 2
ymat1 = ymat.reshape(len(ymat),1) # shape: [m,] --> [m,1]
theta1 = theta.reshape(len(theta),1)
hx2y = np.dot(xmat1, theta1) - ymat1 # shape: m x 1
j = 1. /2. /m * np.dot(hx2y.T, hx2y) # shape: 1 x 1
return j
def compute_grad(theta, xmat, ymat):
j_grad = np.zeros(len(theta), dtype=float)
m = len(ymat)
one_v = np.ones(len(xmat))
xmat1 = np.column_stack((one_v, xmat))
ymat1 = ymat.reshape(m,1) # shape: [m,] --> [m,1]
theta1 = theta.reshape(len(theta),1)
hx2y = np.dot(xmat1, theta1) - ymat1
j_grad = 1. /m * np.dot(xmat1.T, hx2y)
j_grad = j_grad.flatten()
return j_grad
Es ist eine Implementierung einer solchen Funktion. Unter Verwendung dieser beiden Funktionen als untergeordnete Funktionen wird die Parametersuche (Theta), die die Kosten minimiert, durch die Gradientenabstiegsmethode (Gradientenabstieg) durchgeführt. Zunächst wird die folgende in Coursera gezeigte Formel unverändert codiert und die Berechnung durchgeführt.
Formel für den Gradientenabstieg:
\theta_i := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta} (x^{(i)}) - y^{(i)}) x_{j}^{(i)} \ \ \ \ \ (simultaneously\ update\ \theta_j\ for\ all\ j)
def gradient_descent(theta, alpha, num_iters):
global xmat, ymat
m = len(ymat) # number of train examples
j_history = np.zeros(num_iters)
#
for iter in range(num_iters):
xmat1 = xmat ; ymat1 = ymat
delta_t = alpha * compute_grad(theta, xmat1, ymat1)
theta = theta - delta_t
# for DEBUG #
j_history[iter] = compute_cost(theta, xmat, ymat)
return theta, j_history
Das einfachste Gradientenabstiegsverfahren ist wie oben beschrieben. Coursera / Maschinelles Lernen Dies ist kein Problem für die erste Aufgabe. Die gefundene Anpassungslinie ist wie folgt.
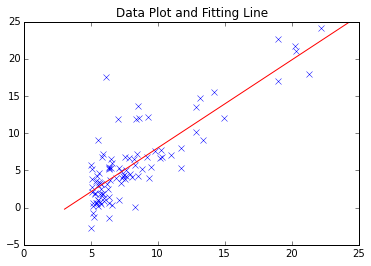
Angesichts der Konvergenz größerer Datenmengen und komplexer Datenanalysen sowie der Reaktion auf lokale Mindestpunkte kann es jedoch Fälle geben, in denen die Verwendung eines bewährten Moduls verlockend ist.
Versuchen Sie es mit scipy.optimize.minimize ()
In Scipy sind verschiedene Funktionen zur Optimierung implementiert.
http://docs.scipy.org/doc/scipy/reference/optimize.html
Dieses Mal habe ich mich für ** scipy.optimize.minimize () ** entschieden, das die Funktion "Minimieren der Funktion, die sich auf den Parameter bezieht" hat. Auszug aus der Dokumentation.
scipy.optimize.minimize (fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)
parameters
- fun : callable Objective function.
- x0 : ndarray Initial guess.
- args : tuple, optional Extra arguments passed to the objective function and its derivatives (Jacobian, Hessian).
- method : str or callable, optional Type of solver. Should be one of -- ‘Nelder-Mead’ -- ‘Powell’ -- ‘CG’ -- ‘BFGS’ -- ‘Newton-CG’ -- ‘L-BFGS-B’ -- ‘TNC’ -- ‘COBYLA’ -- ‘SLSQP’ -- ‘dogleg’ -- ‘trust-ncg’ -- custom - a callable object If not given, chosen to be one of BFGS, L-BFGS-B, SLSQP
- jac : bool or callable, optional (Im Folgenden weggelassen)
Es listet Berechnungsmethoden auf, die ich nicht viel gesehen habe, und es ist ermutigend, obwohl ich mit dem Inhalt nicht vertraut bin. Zuerst habe ich es mit einer einfachen Formel getestet.
import scipy.optimize as spo
def fun1(x):
ans = (x[0] - 1.5) ** 2 + (x[1] - 2.5) ** 2
return ans
def fun1_grad(x):
dx = np.zeros(2)
dx[0] = 2 * x[0] - 3
dx[1] = 2 * x[1] - 5
return dx
x_init = np.array([1.0, 1.0]) # initial value
res1 = spo.minimize(fun1, x_init, method='BFGS', jac=fun1_grad, \
options={'gtol': 1e-6, 'disp': True})
Dies ergibt $ x = [1,5, 2,5] $, wodurch $ f = (x_0 - 1,5) ^ 2 + (x_1 - 2,5) ^ 2 $ minimiert wird. Die Aufgaben von Coursera sind wie folgt. Bereiten Sie zunächst einen Wrapper für die Kostenfunktion und das Derivat vor.
def compute_cost_sp(theta):
global xmat, ymat
j = compute_cost(theta, xmat, ymat)
return j
def compute_grad_sp(theta):
global xmat, ymat
j_grad = compute_grad(theta, xmat, ymat)
return j_grad
Damit soll klargestellt werden, dass der zu durchsuchende Parameter durch Weglassen der Argumente (xmat, ymat) "Theta" ist. Rufen Sie scipy.optimize.minimize () auf, indem Sie eine Funktion oder Ableitung übergeben, die nur "Theta" als Argument verwendet. (Ich soll globale Variablen verwenden ...)
theta_ini = np.zeros(2)
res1 = spo.minimize(compute_cost_sp, theta_ini, method='BFGS', \
jac=compute_grad_sp, options={'gtol': 1e-6, 'disp': True})
print ' theta.processed =', res1.x
Eigentlich ist es möglich, die notwendigen Daten (xmat, ymat) mit ** args ** zu übergeben, ohne einen Wrapper zu schreiben, aber ich war mir bewusst, die "Anpassungsparameter" hier zu klären. Die Berechnungsergebnisse sind wie folgt.
#Eigener Gefälleabstieg(iteration =2000 mal)
theta = -3.788, 1.182
# scipy.optimize.minimize()Ergebnis von
Optimization terminated successfully.
Current function value: 4.476971
Iterations: 4
Function evaluations: 6
Gradient evaluations: 6
theta.processed = [-3.89578088 1.19303364]
Versuche stochastisch zu sein
Von hier aus handelt es sich um eine erweiterte Version, die nicht in der Aufgabe enthalten ist (sie wurde willkürlich ausgeführt). Ich habe versucht, den stochastischen Gradientenabstieg zu "testen", der häufig im Deep Learning verwendet wird.
def stochastic_g_d(theta, alpha, sample_ratio, num_iters):
# calculate the number of sampling data (original size * sample_ratio)
sample_num = int(len(ymat) * sample_ratio)
m = len(ymat) # number of train examples (total)
n = np.size(xmat) / len(xmat)
j_history = np.zeros(num_iters)
for iter in range(num_iters):
xs = np.zeros((sample_num, n)) ; ys = np.zeros(sample_num)
for i in range(sample_num):
myrnd = np.random.randint(m)
xs[i,:] = xmat[myrnd,]
ys[i] = ymat[myrnd]
delta_t = alpha * compute_grad(theta, xs, ys)
theta = theta - delta_t
j_history[iter] = compute_cost(theta, xmat, ymat)
return theta, j_history
Im obigen Code wurde der Prozess von der Abtastung bis zur Minimierung der Zugdaten mit meinem eigenen Code durchgeführt, aber natürlich ist es auch möglich, die Lösung mit scipy.optimize.minimize () nach der Abtastung der Zugdaten zu finden.
Eine ausführliche Erläuterung von S.G.D. (Stochastic Gradient Descent) finden Sie in der Referenz (Webartikel). Das "Herz" besteht darin, die Daten abzutasten, die zur Berechnung der Kostenfunktion und der Ableitung verwendet werden. Da die Anzahl der Zugdaten dieses Mal gering ist und weniger als 100 beträgt, ist es nicht erforderlich, S.G.D. zu verwenden, aber im Fall der Verarbeitung großer Datenmengen kann die Berechnungseffizienz erheblich verbessert werden.
Das Folgende ist eine Zeichnung der Lernkurve. (Horizontale Achse: Anzahl der Schleifenberechnungen, vertikale Achse: Kosten, normale Gradientenabstiegsmethode und stochastische Gradientenmethode.)
Gradient Descent Method (reference)

Stochastic Gradient Descent (sampling/whole data= 0.3)

Es macht Spaß, den Umfang bei Aufgaben mit Cousera selbst erweitern zu können. Ich bin dieses Mal noch mitten im maschinellen Lernen, aber was soll ich neben dem maschinellen Lernen nehmen? Ich denke über verschiedene Dinge nach. In letzter Zeit hat die Anzahl der bezahlten Kurse "Spezialisierung" zugenommen, aber einige der kostenlosen Kurse sind auch von Interesse. (Es braucht viel Zeit, aber ...)
Verweise
- Cousera, Machine Learning (Stanford University) (Ein Handbuch / PDF der Programmieraufgabe wird jede Woche verteilt.)
- Scipy Documentation http://docs.scipy.org/doc/scipy/reference/optimize.html
- Theano, Deep Learning Tutorial http://deeplearning.net/tutorial/ --Qiita: [Update] Erklären Sie die stochastische Gradientenabstiegsmethode, indem Sie sie in Python ausführen http://qiita.com/kenmatsu4/items/d282054ddedbd68fecb0 / d282054ddedbd68fecb0)
- (Serie) Maschinelles Lernen Fangen wir an, Nr. 16 Gradientenmethode zur Optimierung http://gihyo.jp/dev/serial/01/machine-learning/0016
Recommended Posts