Eine aktualisierte Version dieses Artikels ist in meinem Blog verfügbar. Siehe auch hier.

Einführung

In diesem Artikel werde ich ein wenig mathematisch unter Verwendung der Newton-Methode unter Bezugnahme auf Professor Kenichi Kanayas "Optimized Mathematics" [^ Kanatani] überprüfen. Lassen Sie uns gleichzeitig sehen, wie die Optimierung mit Python so aussieht.

Wenn Sie Vorschläge wie "Das ist hier besser" haben, wäre ich Ihnen dankbar, wenn Sie uns im Kommentarbereich eine Anleitung geben könnten.

1.1 Für Variablen

Beginnen wir der Einfachheit halber mit dem Fall einer Variablen. Der Wert der Funktion $ f (x) $ um den Punkt $ \ bar x $ auf der $ x $ -Achse kann von Taylor erweitert werden.

f(\bar x + \Delta x) = f(\bar x) + \frac{df}{dx}(\bar x)\Delta x + \frac{1}{2}\frac{d^2f}{dx^2}(\bar x)\Delta x^2 + O(x^3)

Es wird. ($ ~ O (\ cdot) $ ist Landaus O-Symbol.) Wenn Sie hier die Bedingungen von $ 3 $ und höher ignorieren,

f(\bar x + \Delta x) = f(\bar x) + \frac{df}{dx}(\bar x)\Delta x + \frac{1}{2}\frac{d^2f}{dx^2}(\bar x)\Delta x^2

Es wird. Erwägen Sie, dies zu maximieren. Differenzieren Sie mit $ \ Delta x $ und setzen Sie $ 0 $, um die folgende Gleichung zu erhalten.

\frac{df}{dx}(\bar x) + \frac{d^2f}{dx^2}(\bar x)\Delta x = 0　\tag{1}

Wobei $ f ^ {\ prime} (\ bar x) = \ cfrac {df} {dx} (\ bar x), ~~ f ^ {\ prime \ prime} (\ bar x) = \ cfrac {d Wenn Sie ^ 2f} {dx ^ 2} (\ bar x) $ setzen und nach $ \ Delta x $ auflösen,

\Delta x = - \frac{f^{\prime}(\bar x)}{f^{\prime\prime}(\bar x)}

Es wird. Hier, da $ \ Delta x = x- \ bar x $,

x = \bar x - \frac{f^{\prime}(\bar x)}{f^{\prime\prime}(\bar x)}

erhalten werden kann. Die quadratische Approximation von $ f (x) $ (Approximation durch eine quadratische Funktion) wird durchgeführt, um den Wert von $ x $ zu finden, der den Extremwert der quadratischen Funktion ergibt. Es ist die Bedeutung der Berechnung. Als nächstes wird eine quadratische Näherung um den Wert von $ x $ durchgeführt, der diesen Extremwert ergibt, und der Wert, der zum Extremwert wird, wird gesucht. Die Idee der Newton-Methode besteht darin, sich dem Extremwert von $ f (x) $ schrittweise zu nähern, indem man dies wiederholt.

Zusammenfassend ist das Verfahren wie folgt.

** Newton-Methode (1) **

Geben Sie den Anfangswert von $ x $ an
Aktualisieren Sie wie folgt als $ \ bar x \ leftarrow x . $ x \leftarrow \bar x - \cfrac{f^{\prime}(\bar x)}{f^{\prime\prime}(\bar x)} $$ 3. ~|~x - \bar x~| \leq \delta~Überprüfen Sie, ob dies der Fall ist. Wenn false, kehren Sie zu Schritt 2 zurück. Wenn true, wird x zurückgegeben.

1.1 Beispiel

Versuchen wir die Newton-Methode anhand eines analytisch lösbaren und einfachen Beispiels im Nachschlagewerk. Betrachten Sie die folgende Funktion $ f $.

f(x) = x^3 - 2 x^2 + x + 3

Die Ableitungen erster und zweiter Ordnung sind dies

\frac{df}{dx}(x) = 3x^2 - 4 x + 1\\\\ \frac{d^2f}{dx^2}(x) = 6x - 4

ist. Betrachten Sie nun eine quadratische Näherung.

f(\bar x + \Delta x) = f(\bar x) + \frac{df}{dx}(\bar x)\Delta x + \frac{d^2f}{dx^2}(\bar x)\Delta x^2

$ \ Delta x = x- \ bar x $, also

f(x) = f(\bar x) + \frac{df}{dx}(\bar x)(x - \bar x) + \frac{d^2f}{dx^2}(\bar x)(x - \bar x)^2

Es wird. Zeichnen wir nun die quadratische Näherung um $ f $ und sein $ \ bar x = 2 $ auf derselben Ebene!

f = lambda x: x**3 - 2*x**2 + x + 3
d1f = lambda x: 3*x**2 - 4*x + 1
d2f = lambda x: 6*x - 4
f2 = lambda bar_x, x: f(bar_x) + d1f(bar_x)*(x - bar_x) + d2f(bar_x)*(x - bar_x)**2

x = np.linspace(-10, 10, num=100)
plt.plot(x, f(x), label="original")
plt.plot(x, f2(2, x), label="2nd order approximation")
plt.legend()
plt.xlim((-10, 10))

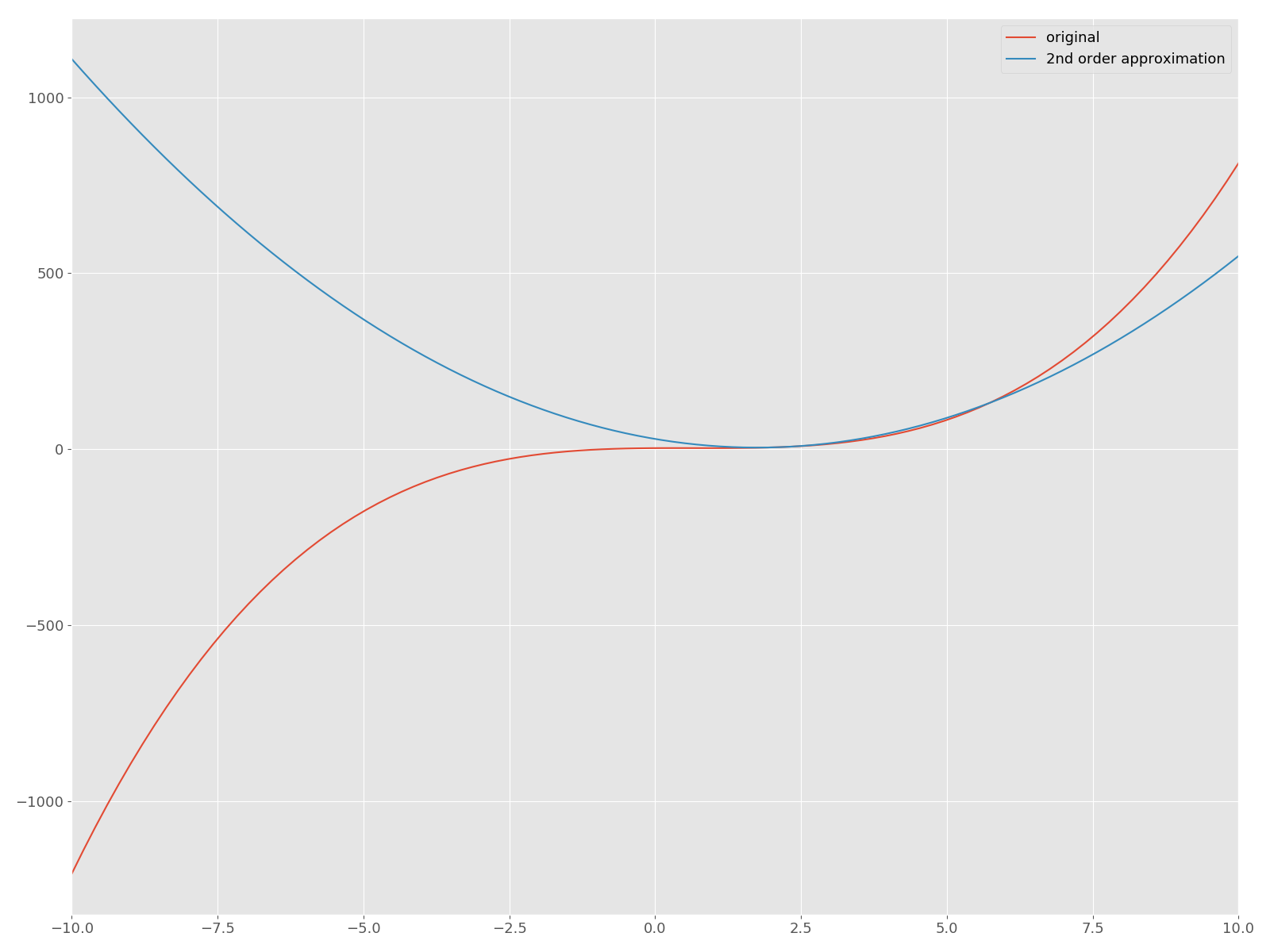
Die rote Kurve ist die ursprüngliche Funktion $ f $ und die blaue quadratische Funktion ist die angenäherte Kurve. Lassen Sie uns nun die Newton-Methode in Python implementieren und eine Lösung finden, die einen Haltepunkt bietet. In diesem Artikel werden wir es nicht wagen, nützliche APIs wie "scipy.optimize" zu verwenden.

`newton_1v.py`


class Newton(object):
    def __init__(self, f, d1f, d2f, f2):
        self.f = f
        self.d1f = d1f
        self.d2f = d2f
        self.f2 = f2

    def _update(self, bar_x):
        d1f = self.d1f
        d2f = self.d2f
        return bar_x - d1f(bar_x)/d2f(bar_x)

    def solve(self, init_x, n_iter, tol):
        bar_x = init_x
        for i in range(n_iter):
            x = self._update(bar_x)
            error = abs(x - bar_x)
            print("|Δx| = {0:.2f}, x = {1:.2f}".format(error, x))
            bar_x = x
            if error < tol:
                break
        return x

def _main():
    f = lambda x: x**3 - 2*x**2 + x + 3
    d1f = lambda x: 3*x**2 - 4*x + 1
    d2f = lambda x: 6*x - 4
    f2 = lambda bar_x, x: f(bar_x) + d1f(bar_x)*(x - bar_x) + d2f(bar_x)*(x - bar_x)**2

    newton = Newton(f=f, d1f=d1f, d2f=d2f, f2=f2)
    res = newton.solve(init_x=10, n_iter=100, tol=0.01)
    print("Solution is {0:.2f}".format(res))

if __name__ == "__main__":
    _main()

Wenn Sie dies tun, erhalten Sie die folgende Ausgabe.

|Δx| = 4.66, x = 5.34
|Δx| = 2.32, x = 3.01
|Δx| = 1.15, x = 1.86
|Δx| = 0.55, x = 1.31
|Δx| = 0.24, x = 1.08
|Δx| = 0.07, x = 1.01
|Δx| = 0.01, x = 1.00
Solution is 1.00

Die Handlung sieht folgendermaßen aus: Sie nimmt monoton gegen 0 ab. Tatsächlich beträgt die erhaltene Lösung 1,00, was mit der analytischen Lösung von 1,00 $ übereinstimmt. Sie können $ 1/3 $ auch erhalten, indem Sie den Anfangswert ändern. Wenn beispielsweise "init_x" "-10" ist, lautet die numerische Lösung "0,33". Wenn jedoch das Gegenteil zurückgegeben wird, bedeutet dies auch, dass die erhaltene Lösung vom Anfangswert abhängt.

Der Code bis zu diesem Punkt wurde auf Gist hochgeladen. Weitere Informationen finden Sie unter hier.

2. Für mehrere Variablen

Als nächstes betrachten wir den Fall mehrerer Variablen. Funktion $ f am Punkt $ [\ bar x_1, ~ \ cdots, ~ \ bar x_n] $ in der Nähe von Punkt $ [\ bar x_1 + \ Delta x_1, ~ \ cdots, ~ \ bar x_n + \ Delta x_n] $ (\ bar x_1, ~ \ cdots, ~ \ bar x_n) Wenn der Wert von $ von Taylor erweitert wird, $ f(\bar x_1 + \Delta x_1,~\cdots,~\bar x_n + \Delta x_n) = \bar f + \sum^{n}_{i=1} \frac{\partial \bar f}{\partial x\_{i}}\Delta x\_i + \frac{1}{2!} \sum^{n}\_{i,~j=1} \frac{\partial^2 \bar f}{\partial x\_i\partial x\_j}\Delta x\_i \Delta x\_j + \cdots $

Es wird. Ich werde diese Entwicklung nicht ableiten, weil sie nicht in den Geltungsbereich dieses Artikels fällt, aber ich denke, es wäre gut, auf Professor Saburo Higuchis Vortrag [^ Taylor] zu verweisen, da er sehr leicht zu verstehen ist.

Kehren wir nun zur Taylor-Erweiterung zurück. Das $ \ bar f $, das früher in der Taylor-Erweiterung verwendet wurde, ist der Wert der Funktion $ f $ am Punkt $ [\ bar x_1, ~ \ cdots, ~ \ bar x_n] $. Ignorieren Sie wie im Fall einer Variablen die Begriffe nach der dritten Ordnung und setzen Sie $ 0 $, nachdem Sie mit $ \ Delta x_i $ differenziert haben.

\frac{\partial \bar f}{\partial x_i} + \sum_{j=1}^{n}\frac{\partial^2 \bar f}{\partial x_i\partial x_j}\Delta x_j = 0

Dies gilt auch für andere Variablen, also angesichts der Hessen-Matrix [^ Hessisch]

\nabla \bar f + \boldsymbol{\bar H}\Delta\boldsymbol{x} = \boldsymbol{0}

ist. $ \ Nabla $ ist ein Symbol namens nabla. Am Beispiel einer Skalarfunktion mit zwei Variablen wird beispielsweise ein Vektor mit einem partiellen Differential erster Ordnung als Element wie unten gezeigt erstellt. Dies wird als Gradient bezeichnet.

\nabla f(x_0,~x_1) = \begin{bmatrix} \cfrac{\partial \bar f}{\partial x_0} \\\\ \cfrac{\partial \bar f}{\partial x_1} \end{bmatrix}

Im Vergleich zu Gleichung (1) können Sie sehen, dass der Gradientenvektor der Ableitung erster Ordnung und die Hessenmatrix der Ableitung zweiter Ordnung entspricht. Lösen wir dies für $ \ boldsymbol {x} $ und achten dabei auf $ \ Delta \ boldsymbol {x} = \ boldsymbol {x} - \ boldsymbol {\ bar x} $.

\boldsymbol{x} = \boldsymbol{\bar x} - \boldsymbol{\bar H}^{-1}\nabla \bar f

Aus dem Obigen ergibt das Newton-Verfahren zu diesem Zeitpunkt das folgende Verfahren.

** Newton-Methode (2) **

Geben Sie den Anfangswert von $ \ boldsymbol {x} $ an
Berechnen Sie die Werte des Gradienten $ \ nabla f $ und der Hessen-Matrix $ \ boldsymbol {H} $ bei $ \ boldsymbol {\ bar x} $.
Berechnen Sie die Lösung der folgenden linearen Gleichung. $ \boldsymbol{H}\Delta\boldsymbol{x} = - \nabla f $
$ \ boldsymbol {x} $ wurde aktualisiert. $ \boldsymbol{x}\leftarrow \boldsymbol{x} + \Delta \boldsymbol{x} $
||\Delta\boldsymbol{x}|| \leq \deltaWenn\boldsymbol{x}Gib es zurück. Wenn false, kehren Sie zu Schritt 2 zurück.

2.1 Beispiel

Betrachten Sie nun die folgende Funktion, die auch im Nachschlagewerk [^ Kanatani] behandelt wird.

f(\boldsymbol{x}) = x_{0}^{3} + x_{1}^{3} - 9x_{0}x_{1} + 27

Eine quadratische Näherung davon um $ \ boldsymbol {\ bar x} = [\ bar x_0, \ bar x_1] $

f(\boldsymbol{x}) = \bar f + \sum^{1}_{i=0}\frac{\partial \bar f}{\partial x\_i}(x\_i - \bar x\_i) + \frac{1}{2!}\sum^{1}\_{i,~j=0}\frac{\partial^2 \bar f}{\partial x\_i\partial x\_j}(x\_i - \bar x\_i)(x\_j - \bar x\_j)

Und der Gradient $ \ nabla f $ und die hessische Matrix $ \ boldsymbol {H} $ sind

\nabla f = \begin{bmatrix} \partial \bar f/\partial x_0 \\\\ \partial \bar f/\partial x_1 \end{bmatrix} = \begin{bmatrix} 3 \bar x_0^2 - 9 \bar x_1 \\\\ 3 \bar x_1^2 - 9 \bar x_0 \end{bmatrix}\\\\ \boldsymbol{H}= \begin{bmatrix} \partial^2 \bar f/\partial x_0^2 & \partial^2 \bar f/\partial x_0\partial x_1 \\\\ \partial^2 \bar f/\partial x_1\partial x_0 & \partial^2 \bar f/\partial x_1^2 \end{bmatrix} = \begin{bmatrix} 6\bar x_0 & -9 \\\\ -9 & 6\bar x_1 \end{bmatrix}

Es wird. Lassen Sie es uns in Python implementieren.

`newton_mult.py`


import numpy as np
import matplotlib.pyplot as plt

plt.style.use("ggplot")
plt.rcParams["font.size"] = 13
plt.rcParams["figure.figsize"] = 16, 12

class MultiNewton(object):
    def __init__(self, f, dx0_f, dx1_f, grad_f, hesse):
        self.f = f
        self.dx0_f = dx0_f
        self.dx1_f = dx1_f
        self.grad_f = grad_f
        self.hesse = hesse

    def _compute_dx(self, bar_x):
        grad = self.grad_f(bar_x)
        hesse = self.hesse(bar_x)
        dx = np.linalg.solve(hesse, -grad)
        return dx

    def solve(self, init_x, n_iter=100, tol=0.01, step_width=1.0):
        self.hist = np.zeros(n_iter)
        bar_x = init_x
        for i in range(n_iter):
            dx = self._compute_dx(bar_x)
            # update
            x = bar_x + dx*step_width
            print("x = [{0:.2f} {1:.2f}]".format(x[0], x[1]))

            bar_x = x
            norm_dx = np.linalg.norm(dx)
            self.hist[i] += norm_dx
            if norm_dx < tol:
                self.hist = self.hist[:i]
                break
        return x

def _main():
    f = lambda x: x[0]**3 + x[1]**3 - 9*x[0]*x[1] + 27
    dx0_f = lambda x: 3*x[0]**2 - 9*x[1]
    dx1_f = lambda x: 3*x[1]**2 - 9*x[0]
    grad_f = lambda x: np.array([dx0_f(x), dx1_f(x)])
    hesse = lambda x: np.array([[6*x[0], -9],[-9, 6*x[1]]])

    init_x = np.array([10, 8])
    solver = MultiNewton(f, dx0_f, dx1_f, grad_f, hesse)
    res = solver.solve(init_x=init_x, n_iter=100, step_width=1.0)
    print("Solution is x = [{0:.2f} {1:.2f}]".format(res[0], res[1]))

    errors = solver.hist
    epochs = np.arange(0, errors.shape[0])

    plt.plot(epochs, errors)
    plt.tight_layout()
    plt.savefig('error_mult.png')

if __name__ == "__main__":
    _main()

Wenn Sie dies tun, erhalten Sie die folgende Ausgabe. Die Lösung ist $ [3, 3] $ und eine der analytischen Lösungen kann erhalten werden.

x = [5.76 5.08]
x = [3.84 3.67]
x = [3.14 3.12]
x = [3.01 3.00]
x = [3.00 3.00]
Solution is x = [3.00 3.00]

Wie wird es schließlich konvergieren?||\Delta x||Es endet mit einem Diagramm des Übergangs von.

abschließend

Bisher haben wir die Newton-Methode für mehrere Variablen beschrieben, obwohl das Beispiel mit einer Variablen beginnt und aus zwei Variablen besteht. Beim Studium von Algorithmen für maschinelles Lernen finden Sie häufig einen Parameter, der einen Referenzwert definiert und den minimalen (oder maximalen) Wert der Funktion angibt. Zu diesem Zeitpunkt verwenden Sie eine Optimierungsmethode wie die Newton-Methode. Ein kurzer Blick auf die mathematischen Formeln mag schwierig erscheinen, aber wenn Sie sie von Grund auf neu lesen, werden Sie feststellen, dass Sie sie unerwartet befolgen können, wenn Sie über Kenntnisse der Universitätsmathematik verfügen.

In den letzten Jahren können Sie Algorithmen für maschinelles Lernen sofort ausprobieren, indem Sie scicit-learn usw. verwenden. Es ist jedoch auch wichtig zu verstehen, was sich darin befindet. Das ist das Ende dieses Artikels.

(Wenn Sie Lust dazu haben, schreiben Sie die Quasi-Newton-Methode usw.)

References [^ Kanatani]: Kenichi Kanaya, "Von den Grundprinzipien der optimierten Mathematik zu Berechnungsmethoden", Kyoritsu Publishing. [^ Taylor]: Kleine Integration / Übung (2006) L09 Taylor-Erweiterung multivariater Funktionen (9.1) Ableitung | Youtube [^ Hessisch]: Extremwertbeurteilung der multivariaten Funktion und der hessischen Matrix | Schöne Geschichte der Mathematik an der High School

[PYTHON] Newton-Methode für maschinelles Lernen (von 1 Variablen zu mehreren Variablen)