[PYTHON] 100 Sprachverarbeitung Knock 2020 Kapitel 8: Neuronales Netz

Neulich wurde 100 Language Processing Knock 2020 veröffentlicht. Ich selbst arbeite erst seit einem Jahr an natürlicher Sprache und kenne die Details nicht, aber ich werde alle Probleme lösen und veröffentlichen, um meine technischen Fähigkeiten zu verbessern.

Alle müssen auf dem Jupiter-Notizbuch ausgeführt werden, und die Einschränkungen der Problemstellung können bequem verletzt werden. Der Quellcode ist auch auf Github. Ja.

Kapitel 7 ist hier.

Die Umgebung ist Python 3.8.2 und Ubuntu 18.04.

Kapitel 8: Neuronales Netz

Implementieren Sie ein Kategorisierungsmodell mit einem neuronalen Netzwerk basierend auf der Kategorisierung der in Kapitel 6 beschriebenen Nachrichtenartikel. Verwenden Sie in diesem Kapitel maschinelle Lernplattformen wie PyTorch, TensorFlow und Chainer.

Verwenden Sie PyTorch.

70. Merkmale nach Summe der Wortvektoren

Ich möchte die in Aufgabe 50 erstellten Trainingsdaten, Verifizierungsdaten und Bewertungsdaten in Matrizen und Vektoren konvertieren. Zum Beispiel möchten wir für Trainingsdaten eine Matrix $ X $ erstellen, in der die Merkmalsvektoren aller Fälle angeordnet sind, und eine Matrix (Vektor) $ Y $, in der die richtigen Antwortbezeichnungen angeordnet sind.

X = \begin{pmatrix} \boldsymbol{x}_1 \ \boldsymbol{x}_2 \ \dots \ \boldsymbol{x}_n \ \end{pmatrix} \in \mathbb{R}^{n \times d}, Y = \begin{pmatrix} y_1 \ y_2 \ \dots \ y_n \ \end{pmatrix} \in \mathbb{N}^{n}

>
 > Hier ist $ n $ die Anzahl der Fälle von Trainingsdaten, und $ \ boldsymbol x_i \ in \ mathbb {R} ^ d $ und $ y_i \ in \ mathbb N $ sind $ i \ in \ {1. \ dots, n \} Repräsentiert den Merkmalsvektor und die korrekte Bezeichnung des $ -ten Falls.
 > Dieses Mal gibt es vier Kategorien: "Business", "Wissenschaft und Technologie", "Unterhaltung" und "Gesundheit". Wenn $ \ mathbb N_4 $ eine natürliche Zahl (einschließlich $ 0 $) kleiner als $ 4 $ darstellt, kann die korrekte Antwortbezeichnung $ y_i $ in jedem Fall durch $ y_i \ in \ mathbb N_4 $ dargestellt werden.
 > Im Folgenden wird die Anzahl der Etikettentypen durch $ L $ dargestellt ($ L = 4 $ in dieser Klassifizierungsaufgabe).
>
 > Der Merkmalsvektor $ \ boldsymbol x_i $ des $ i $ -ten Falls wird durch die folgende Gleichung berechnet.
>
> $$\boldsymbol x_i = \frac{1}{T_i} \sum_{t=1}^{T_i} \mathrm{emb}(w_{i,t})$$
>
 > Hier ist der $ i $ -te Fall $ T_i $ (Artikelüberschrift) Wortketten $ (w_ {i, 1}, w_ {i, 2}, \ dots, w_ {i, T_i}) $ , Und $ \ mathrm {emb} (w) \ in \ mathbb {R} ^ d $ ist ein Wortvektor (die Anzahl der Dimensionen ist $ d $), der dem Wort $ w $ entspricht. Das heißt, $ \ boldsymbol x_i $ ist die Artikelüberschrift des $ i $ -ten Falls, ausgedrückt durch den Durchschnitt der Vektoren der in der Überschrift enthaltenen Wörter. Dieses Mal sollte der in Frage 60 heruntergeladene Wortvektor verwendet werden. Da wir einen Wortvektor mit der Dimension $ 300 $ verwendet haben, ist $ d = 300 $.
 > Die Bezeichnung $ y_i $ des $ i $ -ten Falls ist wie folgt definiert.
>
>```math
y_i = \begin{cases}
0 & (\mbox{Artikel}\boldsymbol x_i\mbox{If ist in der Kategorie "Business"}) \\
1 & (\mbox{Artikel}\boldsymbol x_i\mbox{Ist in der Kategorie "Wissenschaft und Technologie"}) \\
2 & (\mbox{Artikel}\boldsymbol x_i\mbox{If ist in der Kategorie "Unterhaltung"}) \\
3 & (\mbox{Artikel}\boldsymbol x_i\mbox{If ist in der Kategorie "Gesundheit"}) \\
\end{cases}

Wenn zwischen dem Kategorienamen und der Etikettennummer eine Eins-zu-Eins-Entsprechung besteht, muss die Entsprechung nicht der in der obigen Formel angegebenen entsprechen.

Erstellen Sie anhand der obigen Spezifikationen die folgende Matrix / den folgenden Vektor und speichern Sie sie in einer Datei.

• Trainingsdaten-Feature-Matrix: $ X_ {\ rm train} \ in \ mathbb {R} ^ {N_t \ times d} $
• Trainingsdaten-Beschriftungsvektor: $ Y_ {\ rm train} \ in \ mathbb {N} ^ {N_t} $
• Funktionsmatrix für Validierungsdaten: $ X_ {\ rm valid} \ in \ mathbb {R} ^ {N_v \ times d} $
• Validierungsdaten-Beschriftungsvektor: $ Y_ {\ rm valid} \ in \ mathbb {N} ^ {N_v} $
• Funktionsmatrix für Auswertungsdaten: $ X_ {\ rm test} \ in \ mathbb {R} ^ {N_e \ times d} $
• Bewertungsdaten-Beschriftungsvektor: $ Y_ {\ rm test} \ in \ mathbb {N} ^ {N_e} $

Beachten Sie, dass $ N_t, N_v und N_e $ die Anzahl der Fälle von Trainingsdaten, die Anzahl der Fälle von Verifizierungsdaten bzw. die Anzahl der Fälle von Bewertungsdaten sind.

Die Problemstellung ist lang und es ist schwierig, TeX zu korrigieren.

Code

import re
import spacy

In Worte teilen.

Code

nlp = spacy.load('en')
categories = ['b', 't', 'e', 'm']
category_names = ['business', 'science and technology', 'entertainment', 'health']

Code

def tokenize(x):
    x = re.sub(r'\s+', ' ', x)
    x = nlp.make_doc(x)
    x = [d.text for d in x]
    return x

def read_feature_dataset(filename):
    with open(filename) as f:
        dataset = f.read().splitlines()
    dataset = [line.split('\t') for line in dataset]
    dataset_t = [categories.index(line[0]) for line in dataset]
    dataset_x = [tokenize(line[1]) for line in dataset]
    return dataset_x, dataset_t

Code

train_x, train_t = read_feature_dataset('data/train.txt')
valid_x, valid_t = read_feature_dataset('data/valid.txt')
test_x, test_t = read_feature_dataset('data/test.txt')

In einen Feature-Vektor konvertieren.

Code

import torch
from gensim.models import KeyedVectors

Code

model = KeyedVectors.load_word2vec_format('../GoogleNews-vectors-negative300.bin.gz', binary=True)

Code

def sent_to_vector(sent):
    lst = [torch.tensor(model[token]) for token in sent if token in model]
    return sum(lst) / len(lst)

def dataset_to_vector(dataset):
    return torch.stack([sent_to_vector(x) for x in dataset])

Code

train_v = dataset_to_vector(train_x)
valid_v = dataset_to_vector(valid_x)
test_v = dataset_to_vector(test_x)

Code

train_v[0]

Ausgabe

tensor([ 9.0576e-02,  5.4932e-02, -7.7393e-02,  1.1810e-01, -3.8849e-02,
        -2.6074e-01, -6.4484e-02,  3.2715e-02,  1.1792e-01, -3.4363e-02,
        -1.5137e-02, -1.7090e-02,  7.2632e-02,  1.0742e-02,  1.1194e-01,
         5.8945e-02,  1.6275e-01,  1.5393e-01,  7.0496e-02, -1.5210e-01,
         2.8320e-02,  1.1719e-02,  1.9702e-01, -1.5610e-02, -2.3438e-02,
         1.8921e-02,  2.8687e-02, -2.3438e-02,  2.3315e-02, -5.7480e-02,
         2.1973e-03, -1.0449e-01, -9.7534e-02, -1.3694e-01,  1.6144e-01,
        -2.6062e-02,  3.1250e-02,  1.9482e-01, -1.0788e-01,  7.2571e-02,
        -1.3916e-02,  1.1121e-01,  7.0801e-03, -4.1016e-02, -1.9580e-01,
         1.7334e-02,  1.0986e-02, -6.9485e-03,  9.2773e-02,  7.2205e-02,
         6.8298e-02, -5.3589e-02, -1.7447e-01,  1.0245e-01, -8.6426e-02,
        -9.0942e-03, -1.7212e-01, -1.3789e-01, -1.0355e-01,  1.9226e-02,
         1.0620e-02,  9.7626e-02, -5.1147e-02,  1.1371e-01,  3.5156e-02,
        -4.8523e-03, -7.1960e-02,  1.1841e-01, -1.0974e-01,  1.2878e-01,
        -7.3273e-02,  5.3711e-02,  9.6313e-02, -9.0950e-02,  4.3335e-02,
        -4.7424e-02, -3.0518e-02,  5.2856e-02,  3.7842e-02,  2.2559e-01,
         4.0161e-02, -2.3822e-01, -1.3531e-01, -3.8513e-02, -1.1475e-02,
        -7.3242e-02, -1.9324e-01,  1.9553e-01,  1.0870e-01,  1.5405e-01,
         2.8793e-02, -1.9226e-01,  3.1952e-02, -1.0471e-01,  4.9561e-02,
         6.5918e-03, -5.6793e-02,  1.8628e-01, -5.5908e-02, -9.8999e-02,
        -2.1448e-01, -1.6602e-02,  6.7627e-02,  2.1149e-02, -6.8970e-02,
         2.3804e-03, -2.1729e-02, -9.1599e-02, -8.7585e-02, -1.1963e-01,
        -8.7555e-02,  6.1768e-02, -1.6205e-02,  2.9572e-02,  1.2207e-04,
         1.3300e-01,  1.6541e-02, -1.3672e-01,  1.4978e-01, -4.8828e-03,
        -2.6172e-01,  3.9093e-02,  1.4761e-01,  1.3745e-01,  8.6670e-03,
        -1.0797e-01,  8.3801e-02,  3.2690e-01, -6.9336e-02,  6.8115e-02,
         1.0571e-01, -1.2269e-01, -1.4209e-01,  7.7923e-02, -1.6113e-02,
        -6.8039e-02,  1.2909e-02, -4.9911e-02,  2.0142e-01,  9.5764e-02,
         8.1078e-02, -2.6733e-02, -1.4606e-01, -1.0449e-01,  7.1014e-02,
         9.4604e-03,  9.6436e-02, -3.3386e-02, -6.5552e-02, -4.0009e-02,
         2.0976e-01, -9.5825e-02,  1.2494e-01, -1.1230e-02,  1.3062e-02,
         1.8829e-02, -1.7525e-01, -1.6845e-01, -3.0334e-02, -5.6152e-02,
        -2.3193e-02, -8.4961e-02,  4.6021e-02,  1.5533e-01, -2.4780e-02,
        -1.7255e-01, -2.9472e-02, -3.2959e-03, -3.2166e-02,  1.1292e-01,
        -5.0537e-02,  6.0730e-02,  1.8042e-01, -2.6678e-01,  6.5601e-02,
        -2.4567e-01, -4.1382e-02, -2.4902e-02, -7.3853e-02,  3.8330e-02,
        -3.5229e-01, -4.8477e-02,  7.8522e-02,  2.4719e-03, -1.1414e-02,
        -8.9661e-02, -2.4341e-01,  4.9133e-02, -2.7954e-02,  9.2651e-02,
        -4.8340e-02, -5.2063e-02,  5.5817e-02, -3.7842e-03, -1.6852e-01,
         9.8267e-03,  2.1698e-02, -6.5107e-02,  9.8053e-02, -3.6621e-03,
        -2.2009e-01,  1.1389e-01,  5.0537e-02, -1.4322e-01, -8.2336e-02,
        -5.0507e-02, -2.2461e-02, -9.4971e-02, -1.0464e-01, -2.0959e-01,
        -1.2964e-01, -1.0208e-02, -4.0894e-03, -1.4893e-02, -4.9637e-02,
         6.3507e-02, -8.5968e-02,  2.3340e-01,  1.2207e-01, -1.6663e-01,
        -1.6541e-01,  6.9924e-02,  2.4414e-02, -3.3630e-02, -2.2583e-02,
        -2.1289e-01,  8.4106e-02,  1.1916e-01, -1.9623e-02, -3.2654e-02,
        -3.2394e-02,  1.5515e-01, -7.9224e-02, -9.1919e-02, -6.3782e-03,
        -3.6926e-02,  8.0456e-02, -4.5288e-02,  1.9531e-02,  7.4951e-02,
        -8.0195e-02, -2.5232e-01,  1.0986e-01, -1.2573e-01, -1.0083e-01,
         2.0972e-01,  1.3380e-03,  2.2363e-01, -6.7322e-02, -6.3477e-02,
        -2.1167e-01,  5.0659e-03, -3.2227e-02, -2.0752e-02,  2.2107e-01,
        -2.4243e-01,  1.4246e-01,  1.4465e-01, -2.0691e-01, -1.0516e-01,
        -1.0327e-01,  1.6028e-01, -1.4748e-02, -1.9310e-02,  2.3193e-02,
         1.5234e-01,  2.2034e-02, -8.0872e-04, -8.7729e-02,  5.9967e-02,
        -2.6306e-02,  1.3672e-01,  1.5301e-02,  6.3965e-02,  1.9131e-02,
        -5.8695e-02,  1.4355e-01, -9.6710e-02,  7.2235e-02, -1.0620e-02,
         6.1523e-02, -1.2626e-01,  3.3813e-02, -2.1973e-03, -1.3843e-01,
        -1.3458e-01,  5.4447e-02, -2.0325e-01,  1.2244e-01,  4.3335e-02,
        -3.1372e-02, -1.9659e-01, -1.7270e-01,  2.9846e-02, -5.8533e-02,
         6.7017e-02,  1.6748e-01,  1.1859e-01,  1.2134e-01, -1.7578e-02])

Als Gurke speichern.

Code

import pickle

Code

train_t = torch.tensor(train_t).long()
valid_t = torch.tensor(valid_t).long()
test_t = torch.tensor(test_t).long()

Code

with open('data/train.feature.pickle', 'wb') as f:
    pickle.dump(train_v, f)
with open('data/train.label.pickle', 'wb') as f:
    pickle.dump(train_t, f)
    
with open('data/valid.feature.pickle', 'wb') as f:
    pickle.dump(valid_v, f)
with open('data/valid.label.pickle', 'wb') as f:
    pickle.dump(valid_t, f)
    
with open('data/test.feature.pickle', 'wb') as f:
    pickle.dump(test_v, f)
with open('data/test.label.pickle', 'wb') as f:
    pickle.dump(test_t, f)

71. Vorhersage durch einschichtiges neuronales Netzwerk

Lesen Sie die in Frage 70 gespeicherte Matrix und führen Sie die folgenden Berechnungen für die Trainingsdaten durch.

$ {\ Rm softmax} $ ist jedoch die Softmax-Funktion, $ X_ {[1: 4]} \ in \ mathbb {R} ^ {4 \ times d} $ ist der Merkmalsvektor $ \ boldsymbol x_1, \ boldsymbol x_2 , \ boldsymbol x_3, \ boldsymbol x_4 $ sind vertikal angeordnet.

Die Matrix $ W \ in \ mathbb {R} ^ {d \ times L} $ ist die Gewichtsmatrix des einschichtigen neuronalen Netzwerks, die mit einem Zufallswert initialisiert werden kann (gelernt in Aufgabe 73 und höher). .. Beachten Sie, dass $ \ hat {\ boldsymbol y_1} \ in \ mathbb {N} ^ L $ ein Vektor ist, der die Wahrscheinlichkeit der Zugehörigkeit zu jeder Kategorie darstellt, wenn der Fall $ x_1 $ durch die verlernte Matrix $ W $ klassifiziert wird. In ähnlicher Weise drückt $ \ hat {Y} \ in \ mathbb {N} ^ {n \ times L} $ die Wahrscheinlichkeit der Zugehörigkeit zu jeder Kategorie als Matrix für die Trainingsdatenbeispiele $ x_1, x_2, x_3, x_4 $ aus. tun.

Ich denke, dass der Fragesteller wahrscheinlich die Absicht hat, etwas wie "torch.empty (). Normal_ ()" und dann "F.linear ()" zu tun, aber diejenigen, die es wissen, haben bereits "nn". Ich halte es für in Ordnung, Module` zu erben. Ich habe die Absicht der Frage, Menschen, die nicht wissen, was automatische Differenzierung ist, zusammen mit den folgenden Problemen irgendwie dazu zu bringen.

Code

import torch.nn as nn

Code

class Perceptron(nn.Module):
    def __init__(self, v_size, c_size):
        super().__init__()
        self.fc = nn.Linear(v_size, c_size, bias = False)
        nn.init.xavier_normal_(self.fc.weight)
        
    def forward(self, x):
        x = self.fc(x)
        return x

Code

model = Perceptron(300, 4)

Code

x = model(train_v[0])
x = torch.softmax(x, dim=-1)
x

Ausgabe

tensor([0.2450, 0.2351, 0.2716, 0.2483], grad_fn=<SoftmaxBackward>)

Code

x = model(train_v[:4])
x = torch.softmax(x, dim=-1)
x

Ausgabe

tensor([[0.2450, 0.2351, 0.2716, 0.2483],
        [0.2323, 0.2387, 0.2765, 0.2525],
        [0.2093, 0.2120, 0.2750, 0.3037],
        [0.2200, 0.2427, 0.2623, 0.2751]], grad_fn=<SoftmaxBackward>)

Es hat eine richtige Wahrscheinlichkeitsverteilung.

72. Verlust- und Steigungsberechnung

Berechnen Sie den Kreuzentropieverlust und den Gradienten für die Matrix $ W $ für den Fall $ x_1 $ und die Fallmenge $ x_1, x_2, x_3, x_4 $ der Trainingsdaten. Für einen bestimmten Fall $ x_i $ wird der Verlust durch die folgende Gleichung berechnet.

Der Kreuzentropieverlust für die Fallmenge ist jedoch der Durchschnitt der Verluste für jeden in der Menge enthaltenen Fall.

Code

criterion = nn.CrossEntropyLoss()

Code

y = model(train_v[:1])
t = train_t[:1]
loss = criterion(y, t)
model.zero_grad()
loss.backward()
print('Verlust:', loss.item())
print('Steigung')
print(model.fc.weight.grad)

Ausgabe

Verlust: 1.2622126340866089
Steigung
tensor([[ 0.0229,  0.0139, -0.0196,  ...,  0.0300,  0.0307, -0.0044],
        [ 0.0219,  0.0133, -0.0187,  ...,  0.0287,  0.0294, -0.0043],
        [ 0.0201,  0.0122, -0.0172,  ...,  0.0263,  0.0270, -0.0039],
        [-0.0649, -0.0394,  0.0555,  ..., -0.0850, -0.0870,  0.0126]])

Wenn Sie zero_grad () vergessen, wird der Gradient endlos akkumuliert und es wird seltsam.

Code

model.zero_grad()
model.fc.weight.grad

Ausgabe

tensor([[0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]])

Code

y = model(train_v[:4])
t = train_t[:4]
loss = criterion(y, t)
model.zero_grad()
loss.backward()
print('Verlust:', loss.item())
print('Steigung')
print(model.fc.weight.grad)

Ausgabe

Verlust: 1.3049677610397339
Steigung
tensor([[ 0.0044,  0.0014, -0.0114,  ...,  0.0090,  0.0150, -0.0018],
        [-0.0008,  0.0036, -0.0066,  ...,  0.0076,  0.0111, -0.0007],
        [ 0.0038,  0.0008, -0.0114,  ...,  0.0082,  0.0145, -0.0017],
        [-0.0074, -0.0059,  0.0295,  ..., -0.0248, -0.0406,  0.0042]])

73. Lernen durch probabilistische Gradientenabstiegsmethode

Lernen Sie die Matrix $ W $ mit der SGD-Methode (Stochastic Gradient Descent). Das Lernen kann nach einem geeigneten Standard abgeschlossen werden (z. B. "Ende in 100 Epochen").

Zum Zeitpunkt der logistischen Regression haben wir für alle Daten die Quasi-Newton-Methode verwendet. Diesmal handelt es sich jedoch um einen stochastischen Gradientenabstieg. Daher werden wir den Datensatz mischen und nach und nach extrahieren.

Die Dataset-Klasse ist ein untergeordnetes Element mit Daten. Wenn __getitem__ einen ganzzahligen Datenindex empfängt, gibt es die Daten an dieser Adresse zurück.

Code

class Dataset(torch.utils.data.Dataset):
    def __init__(self, x, t):
        self.x = x
        self.t = t
        self.size = len(x)
    
    def __len__(self):
        return self.size
            
    def __getitem__(self, index):
        return {
            'x':self.x[index],
            't':self.t[index],
        }

Die Sampler-Klasse ist ein untergeordnetes Element, das mehrere Indizes eines Datasets in einen Stapel extrahiert und den gesamten Datensatz in Stapel aufteilt.

Code

class Sampler(torch.utils.data.Sampler):
    def __init__(self, dataset, width, shuffle=False):
        self.dataset = dataset
        self.width = width
        self.shuffle = shuffle
        if not shuffle:
            self.indices = torch.arange(len(dataset))
    
    def __iter__(self):
        if self.shuffle:
            self.indices = torch.randperm(len(self.dataset))
        index = 0
        while index < len(self.dataset):
            yield self.indices[index : index + self.width]
            index += self.width

Sie können den Datensatz mischen und abrufen, indem Sie den Datensatz und den Sampler an "torch.utils.data.DataLoader" übergeben.

Code

def gen_loader(dataset, width, sampler=Sampler, shuffle=False, num_workers=8):
    return torch.utils.data.DataLoader(
        dataset, 
        batch_sampler = sampler(dataset, width, shuffle),
        num_workers = num_workers,
    )

Bereiten Sie einen Data Loader mit Trainingsdaten und Verifizierungsdaten vor.

Code

train_dataset = Dataset(train_v, train_t)
valid_dataset = Dataset(valid_v, valid_t)
test_dataset = Dataset(test_v, test_t)
loaders = (
    gen_loader(train_dataset, 1, shuffle = True),
    gen_loader(valid_dataset, 1),
)

Bereiten Sie eine Aufgabe vor, um den Verlust zu berechnen, und einen Trainer, um die Optimierung durchzuführen.

Code

import torch.optim as optim

Code

class Task:
    def __init__(self):
        self.criterion = nn.CrossEntropyLoss()
    
    def train_step(self, model, batch):
        model.zero_grad()
        loss = self.criterion(model(batch['x']), batch['t'])
        loss.backward()
        return loss.item()
    
    def valid_step(self, model, batch):
        with torch.no_grad():
            loss = self.criterion(model(batch['x']), batch['t'])
        return loss.item()

Code

class Trainer:
    def __init__(self, model, loaders, task, optimizer, max_iter, device = None):
        self.model = model
        self.model.to(device)
        self.train_loader, self.valid_loader = loaders
        self.task = task
        self.max_iter = max_iter
        self.optimizer = optimizer
        self.device = device
    
    def send(self, batch):
        for key in batch:
            batch[key] = batch[key].to(self.device)
        return batch
        
    def train_epoch(self):
        self.model.train()
        acc = 0
        for n, batch in enumerate(self.train_loader):
            batch = self.send(batch)
            acc += self.task.train_step(self.model, batch)
            self.optimizer.step()
        return acc / n
            
    def valid_epoch(self):
        self.model.eval()
        acc = 0
        for n, batch in enumerate(self.valid_loader):
            batch = self.send(batch)
            acc += self.task.valid_step(self.model, batch)
        return acc / n
    
    def train(self):
        for epoch in range(self.max_iter):
            train_loss = self.train_epoch()
            valid_loss = self.valid_epoch()
            print('epoch {}, train_loss:{:.5f}, valid_loss:{:.5f}'.format(epoch, train_loss, valid_loss))

Führen Sie das Lernen durch.

Code

model = Perceptron(300, 4)
task = Task()
optimizer = optim.SGD(model.parameters(), 0.1)
trainer = Trainer(model, loaders, task, optimizer, 10)
trainer.train()

Ausgabe

epoch 0, train_loss:0.40178, valid_loss:0.32123
epoch 1, train_loss:0.29685, valid_loss:0.30087
epoch 2, train_loss:0.27381, valid_loss:0.31221
epoch 3, train_loss:0.26309, valid_loss:0.29472
epoch 4, train_loss:0.25435, valid_loss:0.29926
epoch 5, train_loss:0.24851, valid_loss:0.30723
epoch 6, train_loss:0.24424, valid_loss:0.30154
epoch 7, train_loss:0.23987, valid_loss:0.30601
epoch 8, train_loss:0.23762, valid_loss:0.30835
epoch 9, train_loss:0.23378, valid_loss:0.31116

Sie können sehen, dass der Verlust von Trainingsdaten abgenommen hat.

74. Messung der richtigen Antwortrate

Wenn Sie die Fälle von Trainingsdaten und Bewertungsdaten anhand der in Frage 73 erhaltenen Matrix klassifizieren, ermitteln Sie für jede die richtige Antwortrate.

Code

import numpy as np

Code

class Predictor:
    def __init__(self, model, loader):
        self.model = model
        self.loader = loader
        
    def infer(self, batch):
        self.model.eval()
        return self.model(batch['x']).argmax(dim=-1).item()
        
    def predict(self):
        lst = []
        for batch in self.loader:
            lst.append(self.infer(batch))
        return lst

Code

def accuracy(true, pred):
    return np.mean([t == p for t, p in zip(true, pred)])

Code

predictor = Predictor(model, Loader(train_dataset, 1))
pred = predictor.predict()
print('Richtige Antwortrate in den Trainingsdaten:', accuracy(train_t, pred))

Ausgabe

Richtige Antwortrate in den Trainingsdaten: 0.9239049045301385

Code

predictor = Predictor(model, gen_loader(train_dataset, 1))
pred = predictor.predict()
print('Richtige Antwortrate in den Trainingsdaten:', accuracy(train_t, pred))

Ausgabe

Richtige Antwortrate in den Bewertungsdaten: 0.8952095808383234

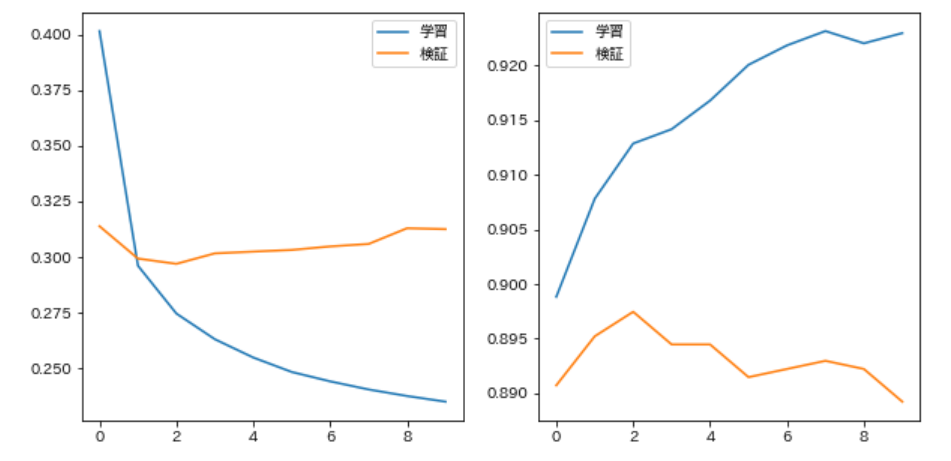
75. Verlust- und Genauigkeitsdiagramm

Durch Ändern des Codes in Q73 können jedes Mal, wenn die Parameteraktualisierung jeder Epoche abgeschlossen ist, der Verlust an Trainingsdaten, die richtige Antwortrate, der Verlust an Entwicklungsdaten und die richtige Antwortrate in einem Diagramm aufgezeichnet werden, um den Lernfortschritt zu überprüfen. Tu es.

Code

import matplotlib.pyplot as plt
import japanize_matplotlib
from IPython.display import clear_output

Es ist ein Code, der die Figur in Echtzeit auf dem Jupyter-Notebook aktualisiert.

Code

class RealTimePlot:
    def __init__(self, legends):
        self.legends = legends
        self.fig, self.axs = plt.subplots(1, len(legends), figsize = (10, 5))
        self.lst = [[[] for _ in xs] for xs in legends]
        
    def __enter__(self):
        return self
        
    def update(self, *args):
        for i, ys in enumerate(args):
            for j, y in enumerate(ys):
                self.lst[i][j].append(y)
        clear_output(wait = True)
        for i, ax in enumerate(self.axs):
            ax.cla()
            for ys in self.lst[i]:
                ax.plot(ys)
            ax.legend(self.legends[i])
        display(self.fig)
        
    def __exit__(self, *exc_info):
        plt.close(self.fig)

Code

class VerboseTrainer(Trainer):
    def accuracy(self, true, pred):
        return np.mean([t == p for t, p in zip(true, pred)])
    
    def train(self, train_v, train_t, valid_v, valid_t):
        train_loader = gen_loader(Dataset(train_v, train_t), 1)
        valid_loader = gen_loader(Dataset(valid_v, valid_t), 1)
        with RealTimePlot([['Lernen', 'Überprüfung']] * 2) as rtp:
            for epoch in range(self.max_iter):
                self.model.to(self.device)
                train_loss = self.train_epoch()
                valid_loss = self.valid_epoch()
                train_acc = self.accuracy(train_t, Predictor(self.model.cpu(), train_loader).predict())
                valid_acc = self.accuracy(valid_t, Predictor(self.model.cpu(), valid_loader).predict())
                rtp.update([train_loss, valid_loss], [train_acc, valid_acc])

Berechnen Sie die richtige Antwortrate im Trainer und wiederholen Sie das Löschen und Anzeigen auf dem Jupyter-Notebook.

Code

model = Perceptron(300, 4)
task = Task()
optimizer = optim.SGD(model.parameters(), 0.1)
trainer = VerboseTrainer(model, loaders, task, optimizer, 10)
train_predictor = Predictor(model, gen_loader(test_dataset, 1))
valid_predictor = Predictor(model, gen_loader(test_dataset, 1))
trainer.train(train_v, train_t, valid_v, valid_t)

76. Kontrollpunkt

Ändern Sie den Code in Frage 75 und schreiben Sie die Prüfpunkte (Werte der Parameter im Lernprozess (Gewichtsmatrix usw.) und den internen Status des Optimierungsalgorithmus) jedes Mal in eine Datei, wenn die Parameteraktualisierung jeder Epoche abgeschlossen ist.

Code

import os

Code

class LoggingTrainer(Trainer):
    def save(self, epoch):
        torch.save({'epoch' : epoch, 'optimizer': self.optimizer}, f'trainer_states{epoch}.pt')
        torch.save(self.model.state_dict(), f'checkpoint{epoch}.pt')
    
    def train(self):
        for epoch in range(self.max_iter):
            train_loss = self.train_epoch()
            valid_loss = self.valid_epoch()
            self.save(epoch)
            print('epoch {}, train_loss:{:.5f}, valid_loss:{:.5f}'.format(epoch, train_loss, valid_loss))

Um das Modell zu speichern, lautet das von state_dict () aufgerufene Wertewörterbuch auch torch.save.

Code

model = Perceptron(300, 4)
task = Task()
optimizer = optim.SGD(model.parameters(), 0.1)
trainer = LoggingTrainer(model, loaders, task, optimizer, 10)
trainer.train()

Ausgabe

epoch 0, train_loss:0.40303, valid_loss:0.31214
epoch 1, train_loss:0.29639, valid_loss:0.29592
epoch 2, train_loss:0.27451, valid_loss:0.29903
epoch 3, train_loss:0.26194, valid_loss:0.29984
epoch 4, train_loss:0.25443, valid_loss:0.29787
epoch 5, train_loss:0.24855, valid_loss:0.30021
epoch 6, train_loss:0.24384, valid_loss:0.30676
epoch 7, train_loss:0.24003, valid_loss:0.30658
epoch 8, train_loss:0.23756, valid_loss:0.30995
epoch 9, train_loss:0.23390, valid_loss:0.30879

Code

ls result/checkpoint*

Ausgabe

result/checkpoint0.pt  result/checkpoint4.pt  result/checkpoint8.pt
result/checkpoint1.pt  result/checkpoint5.pt  result/checkpoint9.pt
result/checkpoint2.pt  result/checkpoint6.pt
result/checkpoint3.pt  result/checkpoint7.pt

Code

ls result/trainer_states*

Ausgabe

result/trainer_states0.pt  result/trainer_states4.pt  result/trainer_states8.pt
result/trainer_states1.pt  result/trainer_states5.pt  result/trainer_states9.pt
result/trainer_states2.pt  result/trainer_states6.pt
result/trainer_states3.pt  result/trainer_states7.pt

77. Mini-Charge

Ändern Sie den Code von Problem 76, berechnen Sie den Verlust / Gradienten für jeden $ B $ -Fall und aktualisieren Sie den Wert der Matrix $ W $ (Mini-Batch). Vergleichen Sie die Zeit, die erforderlich ist, um eine Epoche zu lernen, während Sie den Wert von $ B $ in $ 1, 2, 4, 8, \ dots $ ändern.

Mini-Batch ist bereits in Dataset implementiert, ändern Sie also einfach die Breite von Sampler.

Code

from time import time
from contextlib import contextmanager

Code

@contextmanager
def timer(description):
    start = time()
    yield
    print(description, ': {:.3f}Sekunden'.format(time()-start))

Code

B = [1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024]

Code

task = Task()
for b in B:
    model = Perceptron(300, 4)
    loaders = (
        gen_loader(train_dataset, b, shuffle = True),
        gen_loader(valid_dataset, 1)
    )
    optimizer = optim.SGD(model.parameters(), 0.1 * b)
    trainer = Trainer(model, loaders, task, optimizer, 3)
    with timer(f'Chargengröße{b}'):
        trainer.train()

Ausgabe

epoch 0, train_loss:0.40374, valid_loss:0.31423
epoch 1, train_loss:0.29578, valid_loss:0.29623
epoch 2, train_loss:0.27499, valid_loss:0.29798
Chargengröße 1: 9.657 Sekunden
epoch 0, train_loss:0.39955, valid_loss:0.31440
epoch 1, train_loss:0.29591, valid_loss:0.29844
epoch 2, train_loss:0.27373, valid_loss:0.29537
Chargengröße 2: 5.325 Sekunden
epoch 0, train_loss:0.40296, valid_loss:0.31603
epoch 1, train_loss:0.29613, valid_loss:0.31031
epoch 2, train_loss:0.27469, valid_loss:0.29736
Chargengröße 4: 3.083 Sekunden
epoch 0, train_loss:0.40289, valid_loss:0.31443
epoch 1, train_loss:0.29676, valid_loss:0.30920
epoch 2, train_loss:0.27498, valid_loss:0.30645
Chargengröße 8: 1.982 Sekunden
epoch 0, train_loss:0.40211, valid_loss:0.31350
epoch 1, train_loss:0.29613, valid_loss:0.30777
epoch 2, train_loss:0.27449, valid_loss:0.29903
Chargengröße 16: 1.420 Sekunden
epoch 0, train_loss:0.40343, valid_loss:0.32170
epoch 1, train_loss:0.29695, valid_loss:0.30777
epoch 2, train_loss:0.27486, valid_loss:0.29472
Chargengröße 32: 1.202 Sekunden
epoch 0, train_loss:0.40753, valid_loss:0.32378
epoch 1, train_loss:0.29829, valid_loss:0.29770
epoch 2, train_loss:0.27663, valid_loss:0.30175
Chargengröße 64: 1.060 Sekunden
epoch 0, train_loss:0.41799, valid_loss:0.33559
epoch 1, train_loss:0.30109, valid_loss:0.30401
epoch 2, train_loss:0.27763, valid_loss:0.30351
Chargengröße 128: 0.906 Sekunden
epoch 0, train_loss:0.56407, valid_loss:0.30955
epoch 1, train_loss:0.31099, valid_loss:0.32111
epoch 2, train_loss:0.28797, valid_loss:0.29928
Chargengröße 256: 2.234 Sekunden
epoch 0, train_loss:1.19123, valid_loss:0.32315
epoch 1, train_loss:0.52350, valid_loss:0.39943
epoch 2, train_loss:0.42246, valid_loss:0.36194
Chargengröße 512: 1.323 Sekunden
epoch 0, train_loss:3.77615, valid_loss:0.60957
epoch 1, train_loss:1.05934, valid_loss:0.89198
epoch 2, train_loss:0.80346, valid_loss:0.61814
Chargengröße 1024: 1.057 Sekunden

78. Lernen auf GPU

Ändern Sie den Code in Frage 77 und führen Sie das Training auf der GPU aus.

Wenn Sie es auf "torch.device (" cuda ")" setzen, können Sie weitermachen.

Code

device = torch.device('cuda')
model = Perceptron(300, 4)
task = Task()
loaders = (
    gen_loader(train_dataset, 128, shuffle = True),
    gen_loader(valid_dataset, 1),
)
optimizer = optim.SGD(model.parameters(), 0.1 * 128)
trainer = Trainer(model, loaders, task, optimizer, 3, device=device)
with timer('Zeit'):
    trainer.train()

Ausgabe

epoch 0, train_loss:0.41928, valid_loss:0.31376
epoch 1, train_loss:0.30053, valid_loss:0.29341
epoch 2, train_loss:0.27865, valid_loss:0.29917
Zeit: 1.433 Sekunden

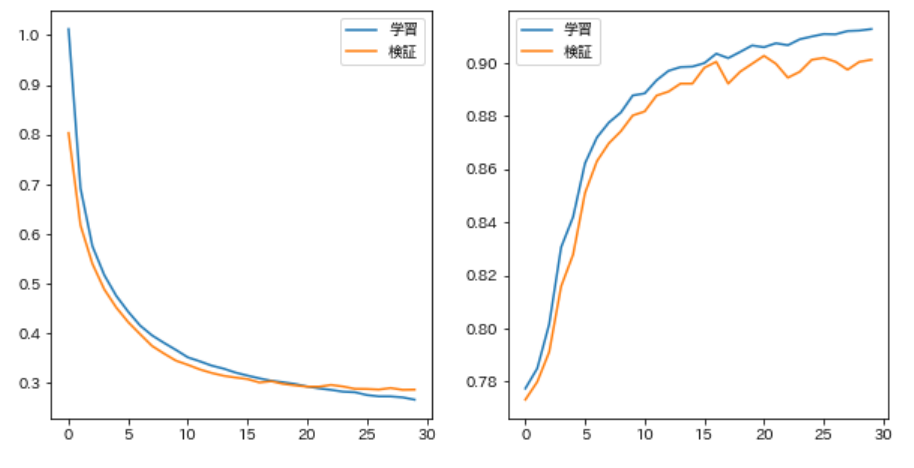
79. Mehrschichtiges neuronales Netzwerk

Ändern Sie den Code von Problem 78 und erstellen Sie einen Hochleistungs-Kategorisierer, während Sie die Form des neuronalen Netzwerks ändern, z. B. das Einführen von Bias-Begriffen und das Überlagern.

Ich habe versucht, es mehrschichtig zu machen, aber es scheint, dass sich die Leistung von selbst nicht wesentlich verbessert.

Code

class ModelNLP79(nn.Module):
    def __init__(self, v_size, h_size, c_size):
        super().__init__()
        self.fc1 = nn.Linear(v_size, h_size)
        self.act = nn.ReLU()
        self.fc2 = nn.Linear(h_size, c_size)
        self.dropout = nn.Dropout(0.2)
        nn.init.kaiming_normal_(self.fc1.weight)
        nn.init.kaiming_normal_(self.fc2.weight)
        
    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.dropout(x)
        x = self.fc2(x)
        return x

Code

model = ModelNLP79(300, 128, 4)
task = Task()
loaders = (
    gen_loader(train_dataset, 128, shuffle = True),
    gen_loader(valid_dataset, 1)
)
optimizer = optim.SGD(model.parameters(), 0.1)
trainer = VerboseTrainer(model, loaders, task, optimizer, 30, device)
trainer.train(train_v, train_t, valid_v, valid_t)

Als nächstes folgt Kapitel 9

100 Language Processing Knock 2020 Kapitel 9: RNN, CNN