[PYTHON] 100 Sprachverarbeitung Knock 2020 Kapitel 7: Word Vector

Neulich wurde 100 Language Processing Knock 2020 veröffentlicht. Ich selbst arbeite erst seit einem Jahr an natürlicher Sprache und kenne die Details nicht, aber ich werde alle Probleme lösen und veröffentlichen, um meine technischen Fähigkeiten zu verbessern.

Alle müssen auf dem Jupiter-Notizbuch ausgeführt werden, und die Einschränkungen der Problemstellung können bequem verletzt werden. Der Quellcode ist auch auf Github. Ja.

Kapitel 6 ist hier.

Die Umgebung ist Python 3.8.2 und Ubuntu 18.04.

Kapitel 7: Wortvektor

Erstellen Sie ein Programm, das die folgende Verarbeitung für einen Wortvektor (Worteinbettung) ausführt, der die Bedeutung eines Wortes als reellen Vektor ausdrückt.

Bitte laden Sie den erforderlichen Datensatz von [hier] herunter (https://nlp100.github.io/ja/ch07.html).

Die heruntergeladene Datei wird unter "Daten" abgelegt.

60. Lesen und Anzeigen von Wortvektoren

Laden Sie den gelernten Wortvektor (3 Millionen Wörter / Phrasen, 300 Dimensionen) in den Google News-Datensatz (ca. 100 Milliarden Wörter) herunter und zeigen Sie den Wortvektor von "USA" an. Beachten Sie jedoch, dass "USA" intern als "United_States" bezeichnet wird.

Verwenden Sie Gensim.

Code

from gensim.models import KeyedVectors

Code

model = KeyedVectors.load_word2vec_format('data/GoogleNews-vectors-negative300.bin.gz', binary=True)

Code

model["United_States"]

Ausgabe

array([-3.61328125e-02, -4.83398438e-02,  2.35351562e-01,  1.74804688e-01,
       -1.46484375e-01, -7.42187500e-02, -1.01562500e-01, -7.71484375e-02,
        1.09375000e-01, -5.71289062e-02, -1.48437500e-01, -6.00585938e-02,
        1.74804688e-01, -7.71484375e-02,  2.58789062e-02, -7.66601562e-02,
       -3.80859375e-02,  1.35742188e-01,  3.75976562e-02, -4.19921875e-02,
       -3.56445312e-02,  5.34667969e-02,  3.68118286e-04, -1.66992188e-01,
       -1.17187500e-01,  1.41601562e-01, -1.69921875e-01, -6.49414062e-02,
       -1.66992188e-01,  1.00585938e-01,  1.15722656e-01, -2.18750000e-01,
       -9.86328125e-02, -2.56347656e-02,  1.23046875e-01, -3.54003906e-02,
       -1.58203125e-01, -1.60156250e-01,  2.94189453e-02,  8.15429688e-02,
        6.88476562e-02,  1.87500000e-01,  6.49414062e-02,  1.15234375e-01,
       -2.27050781e-02,  3.32031250e-01, -3.27148438e-02,  1.77734375e-01,
       -2.08007812e-01,  4.54101562e-02, -1.23901367e-02,  1.19628906e-01,
        7.44628906e-03, -9.03320312e-03,  1.14257812e-01,  1.69921875e-01,
       -2.38281250e-01, -2.79541016e-02, -1.21093750e-01,  2.47802734e-02,
        7.71484375e-02, -2.81982422e-02, -4.71191406e-02,  1.78222656e-02,
       -1.23046875e-01, -5.32226562e-02,  2.68554688e-02, -3.11279297e-02,
       -5.59082031e-02, -5.00488281e-02, -3.73535156e-02,  1.25976562e-01,
        5.61523438e-02,  1.51367188e-01,  4.29687500e-02, -2.08007812e-01,
       -4.78515625e-02,  2.78320312e-02,  1.81640625e-01,  2.20703125e-01,
       -3.61328125e-02, -8.39843750e-02, -3.69548798e-05, -9.52148438e-02,
       -1.25000000e-01, -1.95312500e-01, -1.50390625e-01, -4.15039062e-02,
        1.31835938e-01,  1.17675781e-01,  1.91650391e-02,  5.51757812e-02,
       -9.42382812e-02, -1.08886719e-01,  7.32421875e-02, -1.15234375e-01,
        8.93554688e-02, -1.40625000e-01,  1.45507812e-01,  4.49218750e-02,
       -1.10473633e-02, -1.62353516e-02,  4.05883789e-03,  3.75976562e-02,
       -6.98242188e-02, -5.46875000e-02,  2.17285156e-02, -9.47265625e-02,
        4.24804688e-02,  1.81884766e-02, -1.73339844e-02,  4.63867188e-02,
       -1.42578125e-01,  1.99218750e-01,  1.10839844e-01,  2.58789062e-02,
       -7.08007812e-02, -5.54199219e-02,  3.45703125e-01,  1.61132812e-01,
       -2.44140625e-01, -2.59765625e-01, -9.71679688e-02,  8.00781250e-02,
       -8.78906250e-02, -7.22656250e-02,  1.42578125e-01, -8.54492188e-02,
       -3.18359375e-01,  8.30078125e-02,  6.34765625e-02,  1.64062500e-01,
       -1.92382812e-01, -1.17675781e-01, -5.41992188e-02, -1.56250000e-01,
       -1.21582031e-01, -4.95605469e-02,  1.20117188e-01, -3.83300781e-02,
        5.51757812e-02, -8.97216797e-03,  4.32128906e-02,  6.93359375e-02,
        8.93554688e-02,  2.53906250e-01,  1.65039062e-01,  1.64062500e-01,
       -1.41601562e-01,  4.58984375e-02,  1.97265625e-01, -8.98437500e-02,
        3.90625000e-02, -1.51367188e-01, -8.60595703e-03, -1.17675781e-01,
       -1.97265625e-01, -1.12792969e-01,  1.29882812e-01,  1.96289062e-01,
        1.56402588e-03,  3.93066406e-02,  2.17773438e-01, -1.43554688e-01,
        6.03027344e-02, -1.35742188e-01,  1.16210938e-01, -1.59912109e-02,
        2.79296875e-01,  1.46484375e-01, -1.19628906e-01,  1.76757812e-01,
        1.28906250e-01, -1.49414062e-01,  6.93359375e-02, -1.72851562e-01,
        9.22851562e-02,  1.33056641e-02, -2.00195312e-01, -9.76562500e-02,
       -1.65039062e-01, -2.46093750e-01, -2.35595703e-02, -2.11914062e-01,
        1.84570312e-01, -1.85546875e-02,  2.16796875e-01,  5.05371094e-02,
        2.02636719e-02,  4.25781250e-01,  1.28906250e-01, -2.77099609e-02,
        1.29882812e-01, -1.15722656e-01, -2.05078125e-02,  1.49414062e-01,
        7.81250000e-03, -2.05078125e-01, -8.05664062e-02, -2.67578125e-01,
       -2.29492188e-02, -8.20312500e-02,  8.64257812e-02,  7.61718750e-02,
       -3.66210938e-02,  5.22460938e-02, -1.22070312e-01, -1.44042969e-02,
       -2.69531250e-01,  8.44726562e-02, -2.52685547e-02, -2.96630859e-02,
       -1.68945312e-01,  1.93359375e-01, -1.08398438e-01,  1.94091797e-02,
       -1.80664062e-01,  1.93359375e-01, -7.08007812e-02,  5.85937500e-02,
       -1.01562500e-01, -1.31835938e-01,  7.51953125e-02, -7.66601562e-02,
        3.37219238e-03, -8.59375000e-02,  1.25000000e-01,  2.92968750e-02,
        1.70898438e-01, -9.37500000e-02, -1.09375000e-01, -2.50244141e-02,
        2.11914062e-01, -4.44335938e-02,  6.12792969e-02,  2.62451172e-02,
       -1.77734375e-01,  1.23046875e-01, -7.42187500e-02, -1.67968750e-01,
       -1.08886719e-01, -9.04083252e-04, -7.37304688e-02,  5.49316406e-02,
        6.03027344e-02,  8.39843750e-02,  9.17968750e-02, -1.32812500e-01,
        1.22070312e-01, -8.78906250e-03,  1.19140625e-01, -1.94335938e-01,
       -6.64062500e-02, -2.07031250e-01,  7.37304688e-02,  8.93554688e-02,
        1.81884766e-02, -1.20605469e-01, -2.61230469e-02,  2.67333984e-02,
        7.76367188e-02, -8.30078125e-02,  6.78710938e-02, -3.54003906e-02,
        3.10546875e-01, -2.42919922e-02, -1.41601562e-01, -2.08007812e-01,
       -4.57763672e-03, -6.54296875e-02, -4.95605469e-02,  2.22656250e-01,
        1.53320312e-01, -1.38671875e-01, -5.24902344e-02,  4.24804688e-02,
       -2.38281250e-01,  1.56250000e-01,  5.83648682e-04, -1.20605469e-01,
       -9.22851562e-02, -4.44335938e-02,  3.61328125e-02, -1.86767578e-02,
       -8.25195312e-02, -8.25195312e-02, -4.05273438e-02,  1.19018555e-02,
        1.69921875e-01, -2.80761719e-02,  3.03649902e-03,  9.32617188e-02,
       -8.49609375e-02,  1.57470703e-02,  7.03125000e-02,  1.62353516e-02,
       -2.27050781e-02,  3.51562500e-02,  2.47070312e-01, -2.67333984e-02],
      dtype=float32)

61. Wortähnlichkeit

Berechnen Sie die Kosinusähnlichkeit zwischen "USA" und "USA".

Code

model.similarity("United_States", "U.S.")

Ausgabe

0.73107743

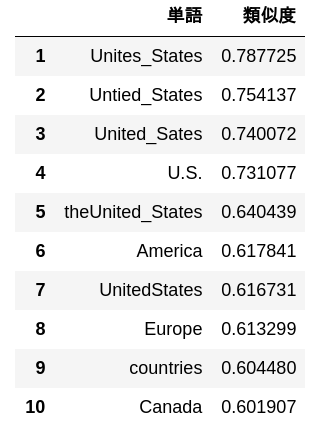
62. 10 Wörter mit hoher Ähnlichkeit

Geben Sie 10 Wörter mit hoher Kosinusähnlichkeit zu "USA" und deren Ähnlichkeit aus.

Code

import numpy as np
import pandas as pd

Code

simularities = model.most_similar("United_States")
pd.DataFrame(
    simularities,
    columns = ['Wort', 'Ähnlichkeitsgrad'],
    index = np.arange(len(simularities)) + 1
)

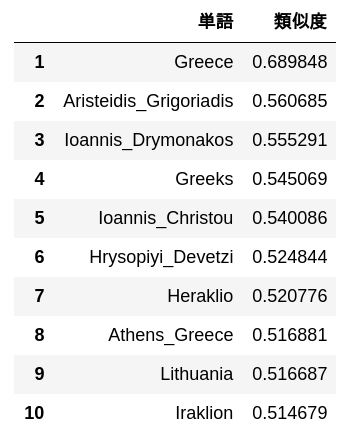
63. Analogie durch additive Zusammensetzung

Subtrahieren Sie den Vektor "Madrid" vom Wortvektor "Spanien", berechnen Sie den Vektor durch Addition des Vektors "Athen" und geben Sie 10 Wörter mit hoher Ähnlichkeit zu diesem Vektor und deren Ähnlichkeit aus.

Code

simularities = model.most_similar(positive=['Spain', 'Athens'], negative=['Madrid'])
pd.DataFrame(
    simularities,
    columns = ['Wort', 'Ähnlichkeitsgrad'],
    index = np.arange(len(simularities)) + 1
)

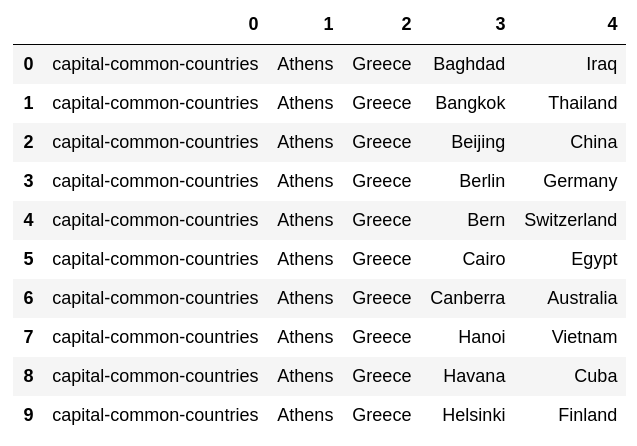
64. Experimentieren Sie mit Analogiedaten

Laden Sie die Bewertungsdaten der Wortanalogie herunter, berechnen Sie vec (Wort in der zweiten Spalte) --vec (Wort in der ersten Spalte) + vec (Wort in der dritten Spalte) und suchen Sie das Wort mit der höchsten Ähnlichkeit zum Vektor. ， Finden Sie die Ähnlichkeit. Fügen Sie das erhaltene Wort und die Ähnlichkeit am Ende jedes Falles hinzu.

Code

with open('data/questions-words.txt') as f:
    lines = f.read().splitlines()

dataset = []
category = None
for line in lines:
    if line.startswith(':'):
        category = line[2:]
    else:
        lst = [category] + line.split(' ')
        dataset.append(lst)

Code

pd.DataFrame(dataset[:10])

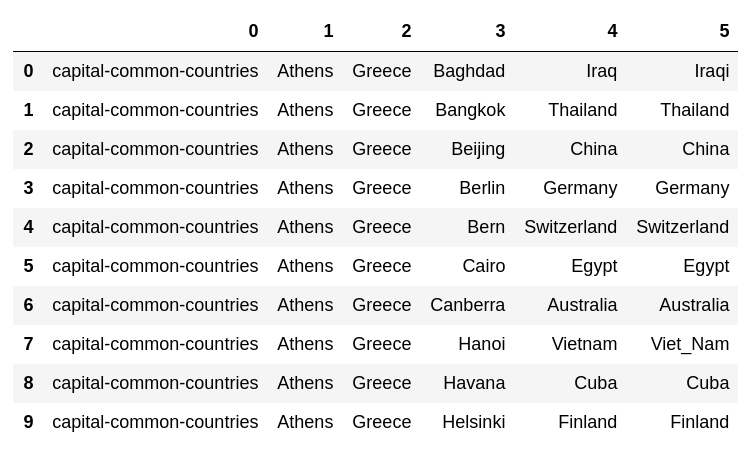
Code

from tqdm import tqdm

Code

for i, lst in enumerate(tqdm(dataset)):
    pred, prob = model.most_similar(positive = lst[2:4], negative = lst[1:2], topn = 1)[0]
    dataset[i].append(pred)

Code

pd.DataFrame(dataset[:10])

65. Richtige Antwortrate bei Analogie-Aufgaben

Verwenden Sie die Ergebnisse von> 64, um die Genauigkeitsrate der semantischen Analogie und der syntaktischen Analogie zu messen.

Die Theorie, dass evalu_word_analogies () verwendet werden sollte, ist allgemein bekannt.

Code

semantic_analogy = [lst[-2:] for lst in dataset if not lst[0].startswith('gram')]
syntactic_analogy = [lst[-2:] for lst in dataset if lst[0].startswith('gram')]

Code

acc = np.mean([true == pred for true, pred in semantic_analogy])
print('Semantische Analogie korrekte Antwortrate:', acc)

Ausgabe

Semantische Analogie korrekte Antwortrate: 0.7308602999210734

Code

acc = np.mean([true == pred for true, pred in syntactic_analogy])
print('Literarische Analogie korrekte Antwortrate:', acc)

Ausgabe

Literarische Analogie korrekte Antwortrate: 0.7400468384074942

66. Bewertung durch WordSimilarity-353

Laden Sie die Bewertungsdaten der WordSimilarity-353-Testsammlung herunter und berechnen Sie den Spearman-Korrelationskoeffizienten zwischen der durch Wortvektoren berechneten Ähnlichkeitsrangfolge und der Rangfolge der Beurteilung der menschlichen Ähnlichkeit.

Code

import zipfile

Code

#Aus Zip-Datei lesen
with zipfile.ZipFile('data/wordsim353.zip') as f:
    with f.open('combined.csv') as g:
        data = g.read()

#Byte-String dekodieren
data = data.decode('UTF-8').splitlines()
data = data[1:]

#Tabulator begrenzt
data = [line.split(',') for line in data]
len(data)

Ausgabe

353

Code

for i, lst in enumerate(data):
    sim = model.similarity(lst[0], lst[1])
    data[i].append(sim)

Code

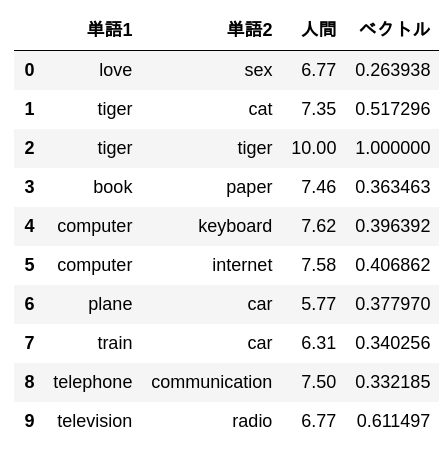
pd.DataFrame(
    data[:10],
    columns = ['Wort 1', 'Wort 2', 'Mensch', 'Vektor']
)

Code

from scipy.stats import spearmanr

Es ist möglich, argsort zweimal anzuwenden, um das Ranking zu erhalten, aber es kann in Bezug auf den Berechnungsbetrag nutzlos sein.

Code

def rank(x):
    args = np.argsort(-np.array(x))
    rank = np.empty_like(args)
    rank[args] = np.arange(len(x))
    return rank

Code

human = [float(lst[2]) for lst in data]
w2v = [lst[3] for lst in data]
human_rank = rank(human)
w2v_rank = rank(w2v)
rho, p_value = spearmanr(human_rank, w2v_rank)

Ausgabe

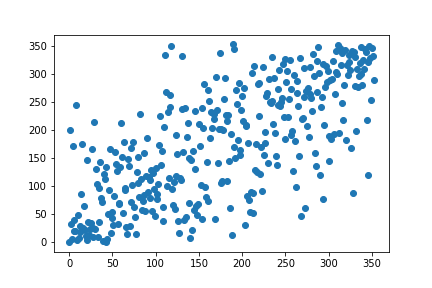
Rangkorrelationskoeffizient: 0.700313895424209
p-Wert: 2.4846350292113526e-53

Code

print('Rangkorrelationskoeffizient:', rho)
print('p-Wert:', p_value)

Code

import matplotlib.pyplot as plt

Code

plt.scatter(human_rank, w2v_rank)
plt.show()

67. k-bedeutet Clustering

Extrahieren Sie den Wortvektor für den Ländernamen und führen Sie k-means Clustering mit der Anzahl der Cluster k = 5 aus.

Ich bin mir nicht sicher, woher ich den Ländernamen beziehen soll, aber der Analogie-Datensatz macht einen guten Job

Code

countries = {
    country
    for lst in dataset
    for country in [lst[2], lst[4]]
    if lst[0] in {'capital-common-countries', 'capital-world'}
} | {
    country
    for lst in dataset
    for country in [lst[1], lst[3]]
    if lst[0] in {'currency', 'gram6-nationality-adjective'}
}
countries = list(countries)
len(countries)

Ausgabe

129

Code

country_vectors = [model[country] for country in countries]

Code

from sklearn.cluster import KMeans

Code

kmeans = KMeans(n_clusters=5)
kmeans.fit(country_vectors)

Ausgabe

KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
       n_clusters=5, n_init=10, n_jobs=None, precompute_distances='auto',
       random_state=None, tol=0.0001, verbose=0)

Code

for i in range(5):
    cluster = np.where(kmeans.labels_ == i)[0]
    print('Klasse', i)
    print(', '.join([countries[k] for k in cluster]))

Ausgabe

Klasse 0
Suriname, Honduras, Tuvalu, Guyana, Venezuela, Peru, Cuba, Ecuador, Nicaragua, Dominica, Colombia, Belize, Mexico, Bahamas, Jamaica, Chile
Klasse 1
Netherlands, Egypt, France, Syria, Finland, Germany, Uruguay, Switzerland, Greenland, Italy, Lebanon, Malta, Algeria, Europe, Tunisia, Brazil, Ireland, England, Libya, Spain, Argentina, Liechtenstein, Iran, Jordan, USA, Iceland, Sweden, Norway, Qatar, Portugal, Denmark, Canada, Israel, Belgium, Morocco, Austria
Klasse 2
Kazakhstan, Lithuania, Turkmenistan, Serbia, Croatia, Greece, Uzbekistan, Armenia, Latvia, Albania, Slovenia, Cyprus, Ukraine, Georgia, Belarus, Bulgaria, Kyrgyzstan, Macedonia, Estonia, Montenegro, Turkey, Azerbaijan, Tajikistan, Poland, Russia, Romania, Hungary, Slovakia, Moldova
Klasse 3
Ghana, Senegal, Zambia, Sudan, Somalia, Zimbabwe, Gabon, Madagascar, Angola, Liberia, Gambia, Niger, Uganda, Mauritania, Namibia, Eritrea, Botswana, Malawi, Mozambique, Guinea, Kenya, Nigeria, Burundi, Mali, Rwanda
Klasse 4
Japan, China, Pakistan, Samoa, Bahrain, Fiji, Australia, India, Laos, Bhutan, Malaysia, Taiwan, Cambodia, Nepal, Korea, Oman, Thailand, Bangladesh, Indonesia, Iraq, Vietnam, Afghanistan, Philippines

Sie sind geteilt.

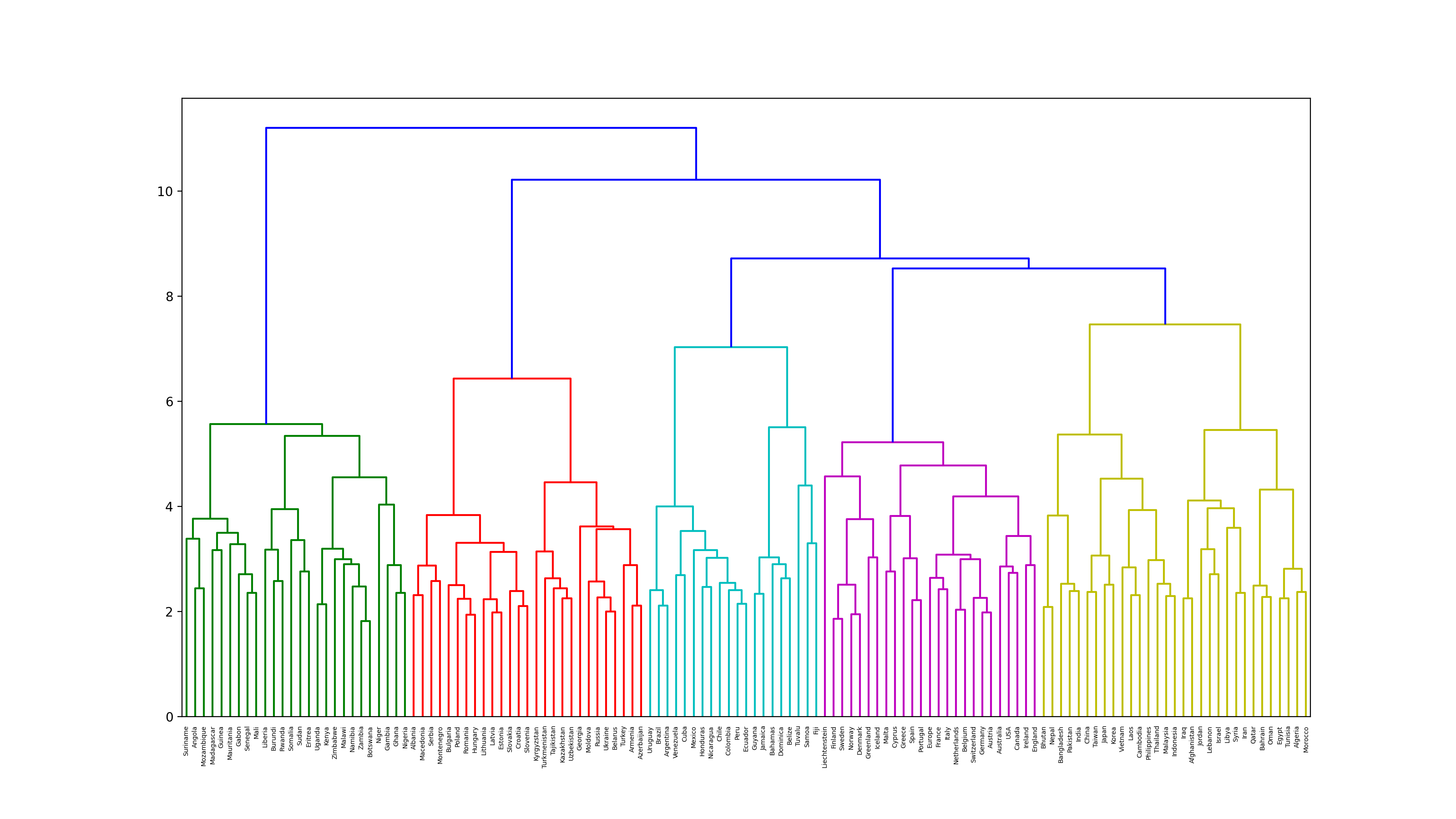
68. Ward Clustering

Führen Sie hierarchische Cluster nach der Ward-Methode für Wortvektoren aus, die sich auf Ländernamen beziehen. Stellen Sie sich das Clustering-Ergebnis außerdem als Dendrogramm vor.

Code

from scipy.cluster.hierarchy import dendrogram, linkage

Code

plt.figure(figsize=(16, 9), dpi=200)
Z = linkage(country_vectors, method='ward')
dendrogram(Z, labels = countries)
plt.show()

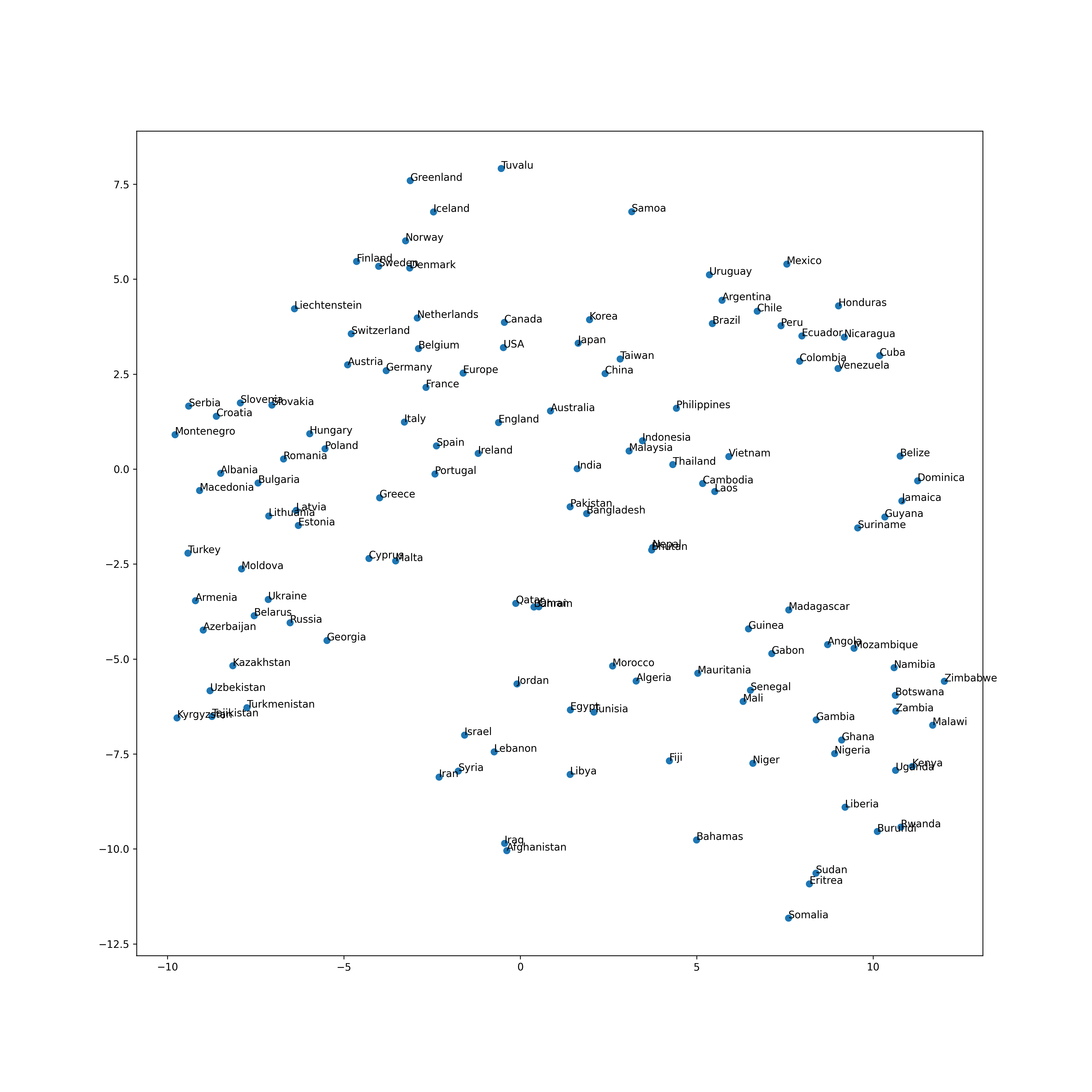
69. Visualisierung mit t-SNE

Visualisieren Sie den Vektorraum von Wortvektoren, die sich auf Ländernamen beziehen, mit t-SNE.

Code

from sklearn.manifold import TSNE

Code

tsne = TSNE()
tsne.fit(country_vectors)

Ausgabe

TSNE(angle=0.5, early_exaggeration=12.0, init='random', learning_rate=200.0,
     method='barnes_hut', metric='euclidean', min_grad_norm=1e-07,
     n_components=2, n_iter=1000, n_iter_without_progress=300, n_jobs=None,
     perplexity=30.0, random_state=None, verbose=0)

Code

plt.figure(figsize=(15, 15), dpi=300)
plt.scatter(tsne.embedding_[:, 0], tsne.embedding_[:, 1])
for (x, y), name in zip(tsne.embedding_, countries):
    plt.annotate(name, (x, y))
plt.show()

Als nächstes folgt Kapitel 8

Sprachverarbeitung 100 Schläge 2020 Kapitel 8: Neuronales Netz