[PYTHON] Zeitreihenanalyse Nr. 6 Gefälschte Rückkehr und republikanischer Teil
1. Übersicht
- In Fortsetzung von Teil 5 studiere ich basierend auf "Zeitreihenanalyse von Wirtschafts- und Finanzdaten".
- In diesem Artikel geht es um die offensichtliche Rückkehr und den republikanischen Teil von Kapitel 6.
2. Gefälschte Rückgabe
Definition
Es scheint eine signifikante Beziehung zwischen $ x_t $ und $ y_t $ zu geben, wenn für zwei nicht verwandte Einheitswurzelprozesse $ x_t $ und $ y_t $ zu $ y_t = \ alpha + \ beta x_t + \ epsilon_t $ zurückgekehrt wird Das Phänomen, das aussieht, wird als gefälschte Rückkehr bezeichnet.
Überprüfung
- Zwei unabhängige Prozesse
$ \ qquad x_t = x_ {t-1} + \ epsilon_ {x, t}, \ quad \ epsilon_ {x, t} \ sim iid (0, \ sigma_x ^ 2) $
$ \ qquad y_t = y_ {t-1} + \ epsilon_ {y, t}, \ quad \ epsilon_ {y, t} \ sim iid (0, \ sigma_y ^ 2) $
$ \ qquad y_t = \ alpha + \ beta x_t + \ epsilon_t $
Kehren Sie zum Modell zurück.
#Datengenerierung
sigma_x, sigma_y = 1, 2
T = 10000
xt = np.cumsum(np.random.randn(T) * sigma_x).reshape(-1, 1)
yt = np.cumsum(np.random.randn(T) * sigma_y).reshape(-1, 1)
- Wenn geplottet, sieht es wie folgt aus.
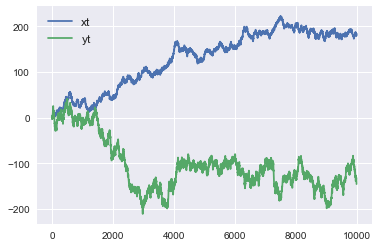
- Zuerst haben wir eine Regression mit scicit-learn durchgeführt.
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(xt,yt)
print('R-squared : ',reg.score(xt,yt))
print('coef : ',reg.coef_, 'intercept', reg.intercept_)
R-squared : 0.4794854506874714
coef : [[-0.62353254]] intercept [-24.27600549]
- Der Entscheidungskoeffizient ($ R ^ 2 $) betrug 0,479, was ein ziemlich hoher Wert war. Für das Regressionsmodell war es in Form von $ \ alpha = -24,28, \ quad \ beta = -0,6235 $.
- Um zu testen, ob $ x_t $ und $ y_t $ unabhängig sind, möchte ich $ H_0 testen: \ beta = 0 $. Eine solche Funktion konnte ich jedoch beim Scicit-Learn nicht finden.
- Als ich nach anderen Bibliotheken suchte, schienen Statistikmodelle nützlich zu sein, also ging ich wieder mit Statistikmodellen zurück.
import statsmodels.api as sm
reg = sm.OLS(yt,sm.add_constant(xt,prepend=False)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.479 |
| Model: |
OLS |
Adj. R-squared: |
0.479 |
| Method: |
Least Squares |
F-statistic: |
9210. |
| Date: |
Tue, 07 Jan 2020 |
Prob (F-statistic): |
0.00 |
| Time: |
22:36:57 |
Log-Likelihood: |
-51058. |
| No. Observations: |
10000 |
AIC: |
1.021e+05 |
| Df Residuals: |
9998 |
BIC: |
1.021e+05 |
| Df Model: |
1 |
|
|
| Covariance Type: |
nonrobust |
|
|
|
coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-24.2760 |
0.930 |
-26.113 |
0.000 |
-26.098 |
-22.454 |
| x1 |
-0.6235 |
0.006 |
-95.968 |
0.000 |
-0.636 |
-0.611 |
- add_constant hängt davon ab, ob ein konstanter Term ($ \ alpha $ in der vorherigen Regressionsgleichung) in das Regressionsmodell aufgenommen werden soll. Wenn Sie add_constant ausführen, wird der konstante Term in das Regressionsmodell aufgenommen. Wenn beim Scicit-Learn das Argument fit_intercept auf False gesetzt ist, hat die Regression keinen konstanten Term. Dies ist oben nicht angegeben, da fit_intercept = True der Standardwert ist.
- Wie beim Scikit-Lernen betrugen die Bestimmungskoeffizienten 0,479, $ \ alpha = -24,28, \ quad \ beta = -0,6235 $, was bestätigt, dass eine äquivalente Regression erreicht wurde.
- Das Schöne an Statistikmodellen ist, dass sie Ihnen 95% signifikante Werte geben. Wenn Sie dies betrachten, wird für $ H_0: \ beta = 0 $ $ H_0 $ abgelehnt, da es bei einem Signifikanzniveau von 95% zwischen -0,636 und -0,611 liegen muss. Dies ist eine gefälschte Rückkehr.
Wie vermeide ich?
Fügen Sie Verzögerungsvariablen in das Modell ein
- Ändern Sie das zurückzugebende Modell wie folgt.
$ \ qquad y_t = \ alpha + \ beta_1 x_t + \ beta_2 y_ {t-1} + \ epsilon_t $
$ y_ {t-1} $ wird zu den erklärenden Variablen von $ y_t $ hinzugefügt.
Wenn Sie mit Statistikmodellen zurückkehren, wird dies wie folgt. sm.OLS verwendet erläuterte Variablen und erklärende Variablen als Argumente, es ist jedoch erforderlich, die erklärenden Variablen wie unten gezeigt in einem Array zusammenzuführen.
x_t, y_t, y_t_1 = xt[1:], yt[1:], yt[:-1]
X = np.column_stack((x_t, y_t_1))
reg = sm.OLS(y_t,sm.add_constant(X)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.999 |
| Model: |
OLS |
Adj. R-squared: |
0.999 |
| Method: |
Least Squares |
F-statistic: |
3.712e+06 |
| Date: |
Thu, 09 Jan 2020 |
Prob (F-statistic): |
0.00 |
| Time: |
22:12:59 |
Log-Likelihood: |
-21261. |
| No. Observations: |
9999 |
AIC: |
4.253e+04 |
| Df Residuals: |
9996 |
BIC: |
4.255e+04 |
| Df Model: |
2 |
|
|
| Covariance Type: |
nonrobust |
|
|
|
coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-0.0815 |
0.049 |
-1.668 |
0.095 |
-0.177 |
0.014 |
| x1 |
-0.0004 |
0.000 |
-0.876 |
0.381 |
-0.001 |
0.000 |
| x2 |
0.9989 |
0.001 |
1964.916 |
0.000 |
0.998 |
1.000 |
- Im Vorgängermodell war das Ergebnis $ \ alpha = -0,0815, \ quad \ beta_1 = -0,0004, \ quad \ beta_2 = 0,9899 $. $ \ Alpha $ und $ \ beta_1 $ sind fast 0, was größtenteils durch $ y_ {t-1} $ erklärt werden kann. Und der Korrelationskoeffizient beträgt 0,999, was so nahe wie möglich an 1 liegt. Beachten Sie auch, dass $ H_0: \ beta_1 = 0 $ nicht abgelehnt wird.
Nehmen Sie den Unterschied des Einheitswurzelprozesses und machen Sie ihn zu einem stetigen Prozess, bevor Sie zurückkehren
- Ändern Sie das zurückzugebende Modell wie folgt.
$ \ qquad \ Delta y_t = \ alpha + \ beta \ Delta x_t + \ epsilon_t $
x_t, y_t = np.diff(xt.flatten()).reshape(-1,1), np.diff(yt.flatten()).reshape(-1,1)
reg = sm.OLS(y_t,sm.add_constant(x_t)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.000 |
| Model: |
OLS |
Adj. R-squared: |
0.000 |
| Method: |
Least Squares |
F-statistic: |
3.297 |
| Date: |
Thu, 09 Jan 2020 |
Prob (F-statistic): |
0.0694 |
| Time: |
22:33:26 |
Log-Likelihood: |
-21262. |
| No. Observations: |
9999 |
AIC: |
4.253e+04 |
| Df Residuals: |
9997 |
BIC: |
4.254e+04 |
| Df Model: |
1 |
|
|
| Covariance Type: |
nonrobust |
|
|
| coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-0.0138 |
0.020 |
-0.681 |
0.496 |
-0.054 |
| x1 |
-0.0374 |
0.021 |
-1.816 |
0.069 |
-0.078 |
- In diesem Fall ist der Korrelationskoeffizient 0, was bei $ \ beta = -0,0374 $ fast 0 ist. Es ist auch nicht möglich, $ H_0: \ beta_1 = 0 $ abzulehnen, was zu der Schlussfolgerung führt, dass es keine signifikante Beziehung zwischen $ \ Delta x_t $ und $ \ Delta y_t $ gibt.
3. Kyowa
Definition
- Sei $ x_t $ und $ y_t $ der Einheitswurzelprozess ($ \ rm I (1) $). Wenn zu diesem Zeitpunkt $ a $ und $ b $ stationäre Prozesse wie $ a x_t + by_t \ sim \ rm I (0) $ sind, besteht eine republikanische Beziehung zwischen $ x_t $ und $ y_t $. Es gibt. Außerdem wird $ (a, b) '$ als republikanischer Vektor bezeichnet.
- Im Allgemeinen existiert für $ \ mathbb y_t \ sim \ rm I (1) $ $ \ mathbb a $, so dass $ \ mathbb a '\ mathbb y_t \ sim \ rm I (0) $ Wenn Sie dies tun, hat $ \ mathbb y_t $ eine republikanische Beziehung. Außerdem wird $ \ mathbb a $ als republikanischer Vektor bezeichnet.
- Zum Beispiel ist $ u_ \ {1t}, u_ \ {2t} $ ein unabhängiger stationärer Prozess und $ w_ \ {1t}, w_ \ {2t} $ ist ein unabhängiger Einheitswurzelprozess.
$ \ qquad \ left \ {\ begin {array} {ll} x_t = \ alpha w_ \ {1t} + u_ \ {1t} \\ y_t = \ beta w_ \ {1t} + u_ \ {2t} \ end { Betrachten Sie das Array} \ right. $
. Zu diesem Zeitpunkt sind sowohl $ x_t $ als auch $ y_t $ $ \ rm I (1) $ Prozesse, aber
$ \ qquad x_t- \ frac {\ alpha} {\ beta} y_t = u_ {1t} - \ Da frac {\ alpha} {\ beta} u_ {2t} \ sim \ rm I (0) $
besteht, besteht eine republikanische Beziehung zwischen $ x_t $ und $ y_t $, und der republikanische Vektor ist . (1, - \ frac {\ alpha} {\ beta}) '.
Implikation
- Wenn $ x_t $ und $ y_t $ Einheitswurzelprozesse sind, wird der langfristige Vorhersagefehler von $ x_t $ und $ y_t $ groß.
- Wenn jedoch eine republikanische Beziehung zwischen $ x_t $ und $ y_t $ besteht, existiert $ a $, so dass $ z_t = y_t - a x_t $ ein stetiger Prozess ist. In diesem Fall ist $ z_t $ langfristig. Es ist möglich, genaue Vorhersagen mit einem gewissen Grad an Genauigkeit zu treffen.
Satz des Granger-Ausdrucks
- Ein VAR-Modell, das eine republikanische Beziehung enthält, kann durch ein Vektorfehlerkorrekturmodell (VECM) dargestellt werden.
- Für das republikanische System $ \ mathbb y_t $ mit VAR (p) -Darstellung
$ \ qquad \ begin {align} \ Delta \ mathbb y_t & = \ zeta_1 \ Delta \ mathbb y_ {t-1} + \ zeta_2 \ Delta \ mathbb y_ {t-2} + \ cdots + \ zeta_ {p-1} \ Delta \ mathbb y_ {t-p + 1} + \ mathbb \ alpha + \ zeta_0 \ Delta \ mathbb y_ {t- 1} + \ epsilon_t \\ & = \ zeta_1 \ Delta \ mathbb y_ {t-1} + \ zeta_2 \ Delta \ mathbb y_ {t-2} + \ cdots + \ zeta_ {p-1} \ Delta \ mathbb y_ {t-p + 1} + \ mathbb \ alpha + - \ mathbb B \ mathbb A '\ mathbb y_ {t-1} + \ epsilon_t \ end {align} $
mit VECM (p-1) Kann ausgedrückt werden.
- $ - \ mathbb B \ mathbb A '\ mathbb y_ {t-1} $ wird als Fehlerkorrekturterm bezeichnet. Hier stellt $ \ mathbb A $ den republikanischen Vektor dar, und der Fehlerkorrekturterm zeigt an, dass die Kraft zur Rückkehr zur Waage wirkt, wenn die Abweichung von der Waage groß wird.
