Versuchen Sie, ein neuronales Netzwerk in Python aufzubauen, ohne eine Bibliothek zu verwenden
Code hier: Der gesamte Code ist auch in Ipython Notebook auf Github verfügbar.
In diesem Beitrag werden wir ein einfaches neuronales Netzwerk mit 1 bis 3 Schichten aufbauen. Ich werde nicht die gesamte Mathematik erklären, die herauskommt, aber ich möchte die notwendigen Teile auf leicht verständliche Weise erklären. Wenn Sie sich für Details der Mathematik interessieren, sind die meisten auf Englisch, aber hier sind einige hilfreiche Links.
- Es wird davon ausgegangen, dass die Leser dieses Beitrags zumindest die Grundlagen der Differenzierung und des maschinellen Lernens (Klassifizierung, Regularisierung usw.) kennen. Es ist sogar noch besser, wenn Sie Optimierungstechniken wie Gradient Descent kennen. Selbst wenn Sie das oben Gesagte nicht kennen, denke ich, dass jeder, der sich für neuronale Netze interessiert, es genießen kann.
Warum müssen wir also ein neuronales Netzwerk von Grund auf neu aufbauen, ohne eine Bibliothek zu verwenden? Aus diesem Grund plane ich, in einem späteren Beitrag neuronale Netzwerkbibliotheken wie PyBrain und Tensorflow zu verwenden. Die Erfahrung, ein neuronales Netzwerk von Grund auf neu aufzubauen, ist äußerst wertvoll. Lassen Sie uns ein Modell entwerfen, indem wir wissen, wie das neuronale Netzwerk funktioniert und aufgebaut ist! Es ist in solchen Zeiten nützlich.
Eine Einschränkung ist, dass sich dieser Beitrag auf die Lesbarkeit konzentriert, sodass der folgende Code nicht effizient geschrieben wird. Ich werde in einem späteren Beitrag erklären, wie man effizienten Code schreibt. Verwenden Sie in diesem Fall Theano.
Daten generieren
Lassen Sie uns nun zuerst die Daten generieren. Glücklicherweise verfügt Scikit-learn über ein verwendbares Kit zur Generierung von Datensätzen, sodass Sie keinen eigenen Code schreiben müssen. Dieses Mal erstellen wir mondförmige Daten mit der Funktion make_moons.
#Daten generieren und zeichnen
np.random.seed(0)
X, y = sklearn.datasets.make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)

Es gibt zwei Klassen generierter Daten (rote und blaue Punkte in der Grafik). Betrachten Sie beispielsweise die blauen Punkte als männliche und rote Punkte als weibliche Patientendatenproben und die X- und Y-Achse als spezifische Messungen.
Unser Ziel ist es, das Klassifizierungsmodell so zu trainieren, dass für jeden Stichprobenpunkt die richtige Klasse vorhergesagt und angegeben wird. Es ist zu beachten, dass diese Daten nicht durch eine gerade Linie klassifiziert werden können. Daher können lineare Klassifizierer wie die logistische Regression nur dann ein gutes Modell erstellen, wenn Sie Ihre eigenen nichtlinearen Merkmale wie Polynome erstellen. Für diese Daten ist es jedoch möglich, ein gutes Modell zu erstellen, indem die Polynomeigenschaften geführt werden.
Sie können dieses Problem lösen, indem Sie ein neuronales Netzwerk führen. Weil Sie kein Feature Engineering durchführen müssen. Die verborgene Schicht des neuronalen Netzwerks findet die Eigenschaften.
Logistische Rückgabe
Bevor wir das neuronale Netzwerk erklären, wollen wir zunächst das logistische Regressionsmodell trainieren. Die Eingabedaten sind ein Punkt auf der X / Y-Achse und die Ausgabedaten sind ihre Klasse (0 oder 1). Hier ist eine Vorbereitung für die Erklärung des neuronalen Netzwerks unten. Erstellen wir also ein logistisches Regressionsmodell mit Schikit-Learn.
#Trainieren Sie ein logistisches Regressionsmodell
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X, y)
#Zeichnen Sie die Entscheidungsgrenze
plot_decision_boundary(lambda x: clf.predict(x))
plt.title("Logistic Regression")

In der Grafik direkt darüber wird das logistische Regressionsmodell trainiert und die Klassen werden mit der Entscheidungsgrenze als Grenze klassifiziert. Dieser Rand führt eine gerade Linie und klassifiziert sie so weit wie möglich, erkennt jedoch nicht den "Monat" der Daten.
Trainiere ein neuronales Netzwerk
Bauen wir nun ein dreischichtiges neuronales Netzwerk auf (1 Eingangsschicht, 1 verborgene Schicht, 1 Ausgangsschicht). Die Anzahl der Knoten in der Eingabeebene (Kreise in der folgenden Abbildung) entspricht der Anzahl der Dimensionen der Daten (diesmal 2). Und die Anzahl der Knoten in der Ausgabeschicht ist die Anzahl der Klassen, diesmal auch 2 (Da es sich übrigens um 2 Klassen handelt, ist es möglich, einen von 1 oder 0 zu einem Ausgabeknoten zu machen, später jedoch mehrere Klassen Dieses Mal werden wir unter Berücksichtigung der Handhabung zwei Knoten verwenden. Die Eingabe des Netzwerks ist der Punkt (X, Y) und die Ausgabe ist die Wahrscheinlichkeit, entweder Klasse 0 (weiblich) oder Klasse 1 (männlich) zu sein. Bitte beachten Sie die Abbildung unten.

Bestimmen Sie als Nächstes die Abmessungen der verborgenen Ebene (die Anzahl der Knoten). Mit zunehmender Anzahl von Knoten mit versteckten Ebenen können komplexere Modelle erstellt werden. Andererseits ist mit zunehmender Anzahl von Knoten Rechenleistung erforderlich, um Parameter zu lernen und vorherzusagen. Es ist auch wichtig zu beachten, dass das Risiko einer Überanpassung mit zunehmender Anzahl von Parametern zunimmt.
Wie wählst du die Anzahl der versteckten Ebenen? Obwohl es allgemeine Richtlinien gibt, erfolgt die Auswahl von Fall zu Fall und sollte eher als Kunst als als Wissenschaft betrachtet werden. Im Folgenden werden wir mit einigen unterschiedlichen Anzahlen versteckter Ebenen experimentieren, um zu sehen, wie sie sich auf die Ausgabe auswirken.
Eine andere zu entscheidende Sache ist die Aktivierungsfunktion für versteckte Schichten. Dies ist eine Funktion zum Transformieren und Ausgeben der Eingabedaten. Sie können nichtlineare Daten trainieren, indem Sie eine nichtlineare Aktivierungsfunktion ausführen. Häufige Beispiele für Aktivierungsfunktionen sind Tanh, Sigmaid Function. Sigmoid_function) und ReLUs. Dieses Mal werde ich Tanh verwenden, was in verschiedenen Fällen zu relativ guten Ergebnissen führen kann. Eine praktische Eigenschaft dieser Funktion ist, dass Sie den ursprünglichen Wert führen und den differenzierten Wert berechnen können. Zum Beispiel ist der Differenzwert von $ tanhx $ $ 1-tanh ^ 2x $. Sobald $ tanhx $ berechnet ist, kann es daher später wiederverwendet werden.
Dieses Mal möchte ich der Ausgabe eine Wahrscheinlichkeit geben, daher werde ich die Softmax-Funktion für die Aktivierungsfunktion der Ausgabeebene verwenden. Sie können nicht wahrscheinliche Zahlen in Wahrscheinlichkeiten konvertieren, indem Sie diese Funktion ausführen. Wenn Sie mit dem logistischen Regressionsmodell vertraut sind, stellen Sie sich die Softmax-Funktion als verallgemeinerte Version mehrerer Klassen vor.
Wie die Vorhersage neuronaler Netze funktioniert
Dieses neuronale Netzwerk verwendet eine Art Matrixmultiplikation, die als Vorwärtsausbreitung bezeichnet wird, und eine Anwendung der oben definierten Aktivierungsfunktion. Wenn die Eingabe x zweidimensional ist, wird der vorhergesagte Wert $ \ hat {y} $ (ebenfalls zweidimensional) wie folgt berechnet.
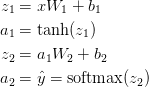
$ z_i $ ist die Eingabeebene i und $ a_i $ ist die von der Aktivierungsfunktion konvertierte Ausgabeebene i. $ W_1 $, $ b_1 $, $ W_2 $, $ b_2 $ sind Netzwerkparameter, die aus den Trainingsdaten gelernt werden müssen. Sie können sich das als Matrixtransformation zwischen Netzwerkschichten vorstellen. Wenn Sie sich die Matrixmultiplikation oben ansehen, können Sie die Anzahl der Dimensionen der Matrix sehen. Wenn Sie beispielsweise 500 versteckte Ebenen verwenden, $ W_1 \ in \ mathbb {R} ^ {2 \ times 500} $, $ b_1 \ in \ mathbb {R} ^ {500} $, $ W_2 \ in \ mathbb {R. } ^ {2 \ times 500} $, $ b_2 \ in \ mathbb {R} ^ {2} $. Sie können also sehen, warum das Erhöhen der Größe der verborgenen Ebene auch die Parameter erhöht.
Zugparameter
Das Trainieren der Parameter bedeutet, nach den Parametern zu suchen ($ W_1 $, $ b_1 $, $ W_2 $, $ b_2 $), die den Fehlerwert in den Trainingsdaten minimieren. Wie definieren Sie den Fehlerwert? Die Funktion, die den Fehlerwert misst, wird als Verlustfunktion bezeichnet. Für Softmax die häufig verwendete Verlustfunktion [Kreuzentropie minimieren](https://ja.wikipedia.org/wiki/%E4%BA%A4%E5%B7%AE%E3%82%A8%E3 Blei% 83% B3% E3% 83% 88% E3% 83% AD% E3% 83% 94% E3% 83% BC) (auch als negative log-Wahrscheinlichkeit bezeichnet). Wenn es N Lerndaten gibt und es eine C-Klasse gibt, kann die Verlustfunktion des vorhergesagten Wertes $ \ hat {y} $ für den richtigen Antwortwert y wie folgt geschrieben werden.

Diese Methode mag kompliziert erscheinen, aber ihre Rolle ist so einfach wie das Addieren der Trainingsdaten und das Hinzufügen des Werts zum Verlust, wenn die Klasse versehentlich vorhergesagt wird. Je weiter die beiden Wahrscheinlichkeitsverteilungen des vorhergesagten Wertes $ \ hat {y} $ und des richtigen Antwortwerts y entfernt sind, desto größer ist der Verlust. Die Suche nach einem Parameter, der den Verlust minimiert, entspricht daher der Maximierung der Wahrscheinlichkeit von Trainingsdaten.
Verwenden Sie den Gradientenabstieg, um den minimalen Verlustwert zu berechnen. Dieses Mal werde ich einen einfachen Batch-Gradientenabstieg durchführen (Lernrate ist konstant), aber probabilistischer Gradientenabstieg E7% 9A% 84% E5% 8B% BE% E9% 85% 8D% E9% 99% 8D% E4% B8% 8B% E6% B3% 95) und Mini-Batch-Gradientenabstieg wären praktischer. Es ist auch praktischer, die Lernrate schrittweise zu reduzieren.
Als Eingabe werden Gradientenabstiegsparameter ($ \ frac {\ partiell {L}} {\ partiell {W_1}} $, $ \ frac {\ partiell {L}} {\ partiell {b_1}} $, $ \ frac { Berechnen Sie die Steigung der Verlustfunktion (Differenzwert des Vektors) für \ partielle {L}} {\ partielle {W_2}} $, $ \ frac {\ partielle {L}} {\ partielle {b_2}} $) wird gebraucht. Verwenden Sie den Back-Propagation-Algorithmus, um diese Steigung zu berechnen. Dieser Algorithmus ist eine effiziente Methode zur Berechnung der Steigung aus der Ausgabe. Diejenigen, die an diesem mathematischen Kommentar interessiert sind, sind hier und [hier](http://cs231n.github.io/optimization- Bitte lesen Sie die Erklärung in 2 /).
Bei Verwendung der Rückübertragung gilt Folgendes.

Schreiben Sie tatsächlich den Code
Lassen Sie uns das bisherige akademische Wissen beenden und den Code tatsächlich schreiben! Lassen Sie uns zunächst die Variablen und Parameter für den Gradientenabstieg festlegen.
num_examples = len(X) #Datengröße für das Training
nn_input_dim = 2 #Anzahl der Dimensionen der Eingabeebene
nn_output_dim = 2 #Anzahl der Dimensionen der Ausgabeschicht
# Gradient descent parameters (Verwenden Sie häufig verwendete Werte)
epsilon = 0.01 #Lernrate mit Gradientenabstieg
reg_lambda = 0.01 #Stärke der Regularisierung
Schreiben wir die oben definierte Verlustfunktion. Sie können dies veranlassen, um die Leistung Ihres Modells zu überprüfen.
#Hilfsfunktion zur Berechnung aller Verluste
def calculate_loss(model):
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
#Vorwärtsausbreitung zur Berechnung von Prognosen
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
#Verlust berechnen
corect_logprobs = -np.log(probs[range(num_examples), y])
data_loss = np.sum(corect_logprobs)
#Geben Sie Loss einen Reguratisierungsbegriff(optional)
data_loss += reg_lambda/2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))
return 1./num_examples * data_loss
Schreiben Sie eine Hilfsfunktion, um die Ausgabeebene zu berechnen. Führt die oben beschriebene Vorwärtsausbreitung an und gibt die höchste Wahrscheinlichkeit zurück.
# Helper function to predict an output (0 or 1)
def predict(model, x):
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
# Forward propagation
z1 = x.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
return np.argmax(probs, axis=1)
Schreiben Sie abschließend den Code, um das neuronale Netzwerk zu generieren. Schreiben Sie einen Batch-Gradientenabstieg unter Verwendung der oben beschriebenen Backpropagation-Differentiale.
# This function learns parameters for the neural network and returns the model.
# - nn_hdim: Number of nodes in the hidden layer
# - num_passes: Number of passes through the training data for gradient descent
# - print_loss: If True, print the loss every 1000 iterations
def build_model(nn_hdim, num_passes=20000, print_loss=False):
# Initialize the parameters to random values. We need to learn these.
np.random.seed(0)
W1 = np.random.randn(nn_input_dim, nn_hdim) / np.sqrt(nn_input_dim)
b1 = np.zeros((1, nn_hdim))
W2 = np.random.randn(nn_hdim, nn_output_dim) / np.sqrt(nn_hdim)
b2 = np.zeros((1, nn_output_dim))
# This is what we return at the end
model = {}
# Gradient descent. For each batch...
for i in xrange(0, num_passes):
# Forward propagation
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
# Backpropagation
delta3 = probs
delta3[range(num_examples), y] -= 1
dW2 = (a1.T).dot(delta3)
db2 = np.sum(delta3, axis=0, keepdims=True)
delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))
dW1 = np.dot(X.T, delta2)
db1 = np.sum(delta2, axis=0)
# Add regularization terms (b1 and b2 don't have regularization terms)
dW2 += reg_lambda * W2
dW1 += reg_lambda * W1
# Gradient descent parameter update
W1 += -epsilon * dW1
b1 += -epsilon * db1
W2 += -epsilon * dW2
b2 += -epsilon * db2
# Assign new parameters to the model
model = { 'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
# Optionally print the loss.
# This is expensive because it uses the whole dataset, so we don't want to do it too often.
if print_loss and i % 1000 == 0:
print "Loss after iteration %i: %f" %(i, calculate_loss(model))
return model
Neuronales Netz mit 3 versteckten Schichten
Erstellen wir nun ein Netzwerk mit drei versteckten Ebenen.
#Erstellen Sie ein Modell mit einer dreidimensionalen verborgenen Ebene
model = build_model(3, print_loss=True)
#Zeichnen Sie die Entscheidungsgrenze
plot_decision_boundary(lambda x: predict(model, x))
plt.title("Decision Boundary for hidden layer size 3")

Ich habe die Mondform gut erkannt! Sie können die Klassen richtig durch das neuronale Netzwerk unterteilen.
Überprüfen Sie die kompatible Größe der ausgeblendeten Ebene
Oben habe ich 3 versteckte Ebenen ausgewählt. Vergleichen wir unten, während wir die Anzahl der ausgeblendeten Ebenen ändern.
plt.figure(figsize=(16, 32))
hidden_layer_dimensions = [1, 2, 3, 4, 5, 20, 50]
for i, nn_hdim in enumerate(hidden_layer_dimensions):
plt.subplot(5, 2, i+1)
plt.title('Hidden Layer size %d' % nn_hdim)
model = build_model(nn_hdim)
plot_decision_boundary(lambda x: predict(model, x))
plt.show()

In der obigen Abbildung haben wir einen guten Überblick über das Datenmuster bei niedrigdimensionalen verborgenen Schichten (pro 3 oder 4). Andererseits scheint die Gefahr einer Überanpassung bei höheren Abmessungen zu bestehen. In diesem Fall wird die Daten in ihrer Gesamtheit gespeichert, anstatt die wahre Form der Daten zu erfassen. Wenn Sie die Testdaten zur Überprüfung des Modells führen, sollten Sie in der Lage sein, genauer vorherzusagen, dass es sich um eine niedrigdimensionale verborgene Schicht handelt. Es wäre (computertechnisch) "wirtschaftlicher", die Versteckschicht der richtigen Größe zu wählen, als die Überanpassung stark zu regulieren.
Nun, diesmal habe ich versucht, ein Netzwerk von Grund auf neu zu erstellen, ohne eine Bibliothek zu verwenden. Als nächstes werde ich das tiefe Lernen unter Verwendung der Bibliothek des neuronalen Netzwerks genauer erklären.
- Geschrieben mit Denny Britz, der den wildML-Blog schreibt
Recommended Posts