[PYTHON] Versuchen Sie es mit TensorFlow-Part 2-Convolution Neural Network (MNIST).

Dieses Mal werden wir Zahlen durch ein Faltungs-Neuronales Netzwerk unter Verwendung von MNIST klassifizieren.

MNIST MNIST ist ein Datensatz handgeschriebener Textbilder von 0 bis 9. Dieser Datensatz enthält 60.000 Trainingsdaten mit einer Bildgröße von 28 x 28. Es enthält 10.000 Testdaten. Die gleiche Anzahl korrekter Etikettendaten ist ebenfalls enthalten.

Verwenden Sie diesen Datensatz, um herauszufinden, wie die Zahlen im Zielbild lauten.

Vorbereitungen

Laden Sie den MNIST-Beispielcode im Voraus herunter.

Ganzer Implementierungscode

Der Implementierungsinhalt basiert auf dem [MNIST-Beispielcode] von TensorFlow (https://github.com/tensorflow/tensorflow/tree/master/tensorflow/examples/tutorials/mnist). Der Inhalt von Deep MNIST for Experts wurde importiert und teilweise geändert.

Der gesamte Implementierungscode lautet wie folgt. Platzieren Sie diesen Quellcode direkt unter dem Verzeichnis mnist des zuvor heruntergeladenen Beispiels. ※ tensorflow/tensorflow/examples/tutorials/mnist

deep_mnist_softmax.py

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import argparse
import sys

from tensorflow.examples.tutorials.mnist import input_data

import tensorflow as tf

#Gewichtsvariable
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

#Vorspannungsvariable
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

#Falten
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

#Pooling
def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')

def main(_):
  #Datenerfassung
  mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

  #Platzhaltererstellung
  x = tf.placeholder(tf.float32, [None, 784])
  y_ = tf.placeholder(tf.float32, [None, 10])

  #1. Faltschicht
  W_conv1 = weight_variable([5, 5, 1, 32])
  b_conv1 = bias_variable([32])
  x_image = tf.reshape(x, [-1,28,28,1])
  h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
  h_pool1 = max_pool_2x2(h_conv1)

  #2. Faltschicht
  W_conv2 = weight_variable([5, 5, 32, 64])
  b_conv2 = bias_variable([64])
  h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
  h_pool2 = max_pool_2x2(h_conv2)

  #Vollständig verbundene Schicht
  W_fc1 = weight_variable([7 * 7 * 64, 1024])
  b_fc1 = bias_variable([1024])
  h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
  h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

  #Dropout-Ebene
  keep_prob = tf.placeholder(tf.float32)
  h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

  #Ausgabeschicht
  W_fc2 = weight_variable([1024, 10])
  b_fc2 = bias_variable([10])
  y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

  #Verlustfunktion (Kreuzentropiefehler)
  cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv, y_))

  #Steigung
  train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

  #Richtigkeit
  correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
  accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

  #Session
  sess = tf.InteractiveSession()
  sess.run(tf.global_variables_initializer())

  #Ausbildung
  for i in range(5000):
    batch = mnist.train.next_batch(50)

    if i % 500 == 0:
      #Fortschritt (alle 500 Fälle)
      train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
      print("step %d, training accuracy %f" % (i, train_accuracy))

    #Durchführung des Trainings
    train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

  #Auswertung
  print("test accuracy %f" % accuracy.eval(feed_dict={
    x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))

if __name__ == '__main__':
  parser = argparse.ArgumentParser()
  parser.add_argument('--data_dir', type=str, default='/tmp/tensorflow/mnist/input_data',
                      help='Directory for storing input data')
  FLAGS, unparsed = parser.parse_known_args()
  tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

neurales Netzwerk

Der Verarbeitungsablauf des obigen Codes und die Form des neuronalen Netzwerks sind wie folgt.

Prozessablauf

gestalten

Details zum Implementierungscode

Die Details des Implementierungscodes werden unten beschrieben.

• Gewicht

#Gewichtsvariable
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

Initialisieren Sie mit einem Zufallswert aus einer Normalverteilung als Gewichtsvariable.

--Vorspannen

#Vorspannungsvariable
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

Initialisieren Sie mit einer Konstanten (0,1) als Bias-Variable.

Form [2, 3] [[0.1, 0.1, 0.1], [0.1, 0.1, 0.1]]

--Falten

#Falten
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

Gewicht (Filtergröße) Geben Sie Schritt Schritte``` und Polsterung``` Polsterung``` in Form von `W``` an Falten Sie es nach oben.

--Poolen

#Pooling
def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')

Geben Sie Schritt Schritte``` und Polsterung``` Polsterung``` in Form der Poolgröße `ksize``` an Führen Sie ein Pooling durch.

ksize: So legen Sie die Poolgröße fest Für 2x2 [1, 2, 2, 1] Für 3x3 [1, 3, 3, 1]

--Datenerfassung

  #Datenerfassung
  mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

Erfasst MNIST-Daten.

• placeholder

 #Platzhaltererstellung
 x = tf.placeholder(tf.float32, [None, 784])
 y_ = tf.placeholder(tf.float32, [None, 10])

Eingabedaten: Erstellen Sie n x 784 als Platzhalter als `x```. Beschriften Sie (korrekte) Daten: Erstellen Sie n x 10 als Platzhalter als `y_```. Der Platzhalter füllt die Daten zur Laufzeit aus.

784 ist der Wert, wenn das 28x28-Bild (= 784) als eine Dimension behandelt wird.

• Faltschicht

#1. Faltschicht
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1,28,28,1])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

#2. Faltschicht
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

Hier wird der Prozess gemäß dem folgenden Ablauf ausgeführt.

1. Mit Filtergröße (5x5) und 32 Ausgängen einklappen
2. Vorspannungsaddition
3. Aktivieren Sie die Aktivierungsfunktion ReLU
4. Pooling in Poolgröße (2x2)
5. Zur zweiten Schicht
6. Filtergröße (5x5) einklappen, Ausgabe 64
7. Führen Sie die gleiche Behandlung wie die erste Schicht mit der vollständig verbundenen Schicht durch

• Volle Haftschicht

#Vollständig verbundene Schicht
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

[7 * 7 * 64, 1024]Ist7 * 7Die Größe, die in der zweiten Schicht der Faltung zusammengefasst wurde, 64Die Anzahl der Ausgänge in der zweiten Faltschicht,1024Ist die Anzahl der Ausgänge der vollständig verbundenen Schicht.

Hier wird der Prozess gemäß dem folgenden Ablauf ausgeführt.

1. Formatieren Sie das Ausgabeergebnis der zweiten Faltungsschicht zur Multiplikation in zwei Dimensionen
2. Multiplizieren Sie mit der Ausgabe der zweiten Faltungsschicht (n, 7 x 7 x 64) und dem Gewicht (7 x 7 x 64, 1024).
3. Vorspannungsaddition
4. Aktivieren Sie die Aktivierungsfunktion ReLU
5. Zur nächsten Schicht

• Drop-Layer

#Dropout-Ebene
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

keep_probGibt die Droprate an.

• Da es sich um einen Platzhalter handelt, geben Sie die Drop-Rate zur Laufzeit ein.

--Ausgabeschicht

#Ausgabeschicht
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

Geben Sie die Anzahl der auszugebenden Klassifikationen an: `` `10```.

• Verlustfunktion / Gradient / Genauigkeit

#Verlustfunktion (Kreuzentropiefehler)
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(y_conv, y_))

#Steigung
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

#Richtigkeit
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

Geben Sie den Kreuzentropiefehler als Verlustfunktion an Geben Sie Adam für den Farbverlauf an. `` `1e-4``` ist die Lernrate. Die Genauigkeit ist der Durchschnitt der richtigen Antworten (Anzahl der richtigen Antworten / n).

--Session

#Session
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())

Erstellen Sie eine Sitzung. Hier,

sess.run(tf.global_variables_initializer())Bei tf.Variable initialisieren.

 - Ausbildung

```python
#Ausbildung
for i in range(5000):
  batch = mnist.train.next_batch(50)

  if i % 500 == 0:
    #Fortschritt (alle 500 Fälle)
    train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})
    print("step %d, training accuracy %f" % (i, train_accuracy))

  #Durchführung des Trainings
  train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

Stellen Sie die Anzahl der Schulungen auf 5000 ein (geben Sie weniger an, da dies Zeit kostet). Lesen Sie in einem Training jeweils 50 Trainingsdaten und führen Sie `` `train_step``` aus. Im weiteren Verlauf wird die Genauigkeit alle 500 Mal ausgedruckt. (Für die Genauigkeitsausgabe dieses Fortschritts werden die Trainingsdaten unverändert als Berechnungsdaten verwendet. Darüber hinaus beträgt die Anzahl der Daten nur 50, sodass die Zuverlässigkeit gering ist.)

Ergänzung · `Mnist.train.next_batch ()` mischt die Daten, wenn sie bis zum Ende gelesen werden Lesen Sie die Daten von Anfang an erneut. - Feed_dict = {x: batch [0], y_: batch [1] `` `gibt Platzhalterdaten ein. - Keep_prob: 0.5``` gibt eine Droprate von 50% an. Wenn 1.0 angegeben ist, wird sie nicht fallen gelassen. Geben Sie 1.0 für die Bewertung und Vorhersage an.

--Auswertung

#Auswertung
print("test accuracy %f" % accuracy.eval(feed_dict={
  x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))

Hier wird die Genauigkeit anhand von 10.000 Testdaten berechnet.

keep_prob ist 1.0 ist angegeben.

## Lauf

 Führen Sie den Code aus.

python deep_mnist_softmax.py

 * Wenn Sie in der Umgebung ausführen, die im vorherigen [Eintrag](http://qiita.com/fujin/items/93aa9144d756eb85004d) erstellt wurde, führen Sie die Ausführung nach dem Starten der virtuellen Umgebung aus.

## Ergebnis

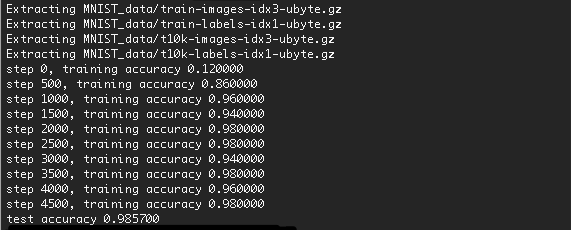
 Das Ausführungsergebnis ist wie folgt.
 Die Genauigkeit wurde auf 98,57% erhöht.
 Durch Erhöhen der Anzahl der Schulungen sollte die Genauigkeit etwas verbessert werden.

 ![sc_2017-02-001.png](https://qiita-image-store.s3.amazonaws.com/0/134550/55eafe53-65bd-e8bd-b73c-1e66b96f2ee0.png)

 > Es wird zum ersten Mal einige Zeit dauern, da die Daten heruntergeladen werden.

 Wie oben erwähnt, führten wir diesmal eine numerische Klassifizierung durch ein Faltungsnetzwerk unter Verwendung von MNIST durch.