2. Multivariate Analyse in Python 7-3. Entscheidungsbaum [Rückgabebaum]

Ein weiterer Aspekt des Entscheidungsbaums, ** Regressionsbaum ** mit der Zielvariablen als numerischen Daten.
Verwenden Sie für den ** Klassifizierungsbaum **, dessen Zielvariable kategoriale Daten sind, den ** DecisionTreeClassifier ** des Moduls scikit-learn.tree, aber den ** DecisionTreeRegressor ** für das ** Regressionsbaum ** -Modell.

⑴ Bibliothek importieren

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.tree import DecisionTreeRegressor #Klasse zum Erstellen eines Regressionsbaummodells

⑵ Datenerfassung und Lesen

from sklearn.datasets import load_boston
boston_dataset = load_boston()

Verwenden Sie für Daten den "Bostoner Immobilienpreis-Datensatz", der mit scikit-learn geliefert wird.
Es gibt 13 Merkmale und 506 Beispiele im Zusammenhang mit der Wohnsituation in Boston, einer großen Stadt im Nordosten der USA.
Ziel dieses Datensatzes ist es, die Immobilienpreise anhand bestimmter Funktionen vorherzusagen.
Das Ziel ist der Preis des Hauses mit dem Variablennamen MEDV (Abkürzung für Medianwert), und die 13 Merkmalsgrößen sind erklärende Variablen für die Vorhersage des Preises des Hauses.
Klicken Sie hier, um Details wie den Inhalt der erklärenden Variablen https://qiita.com/y_itoh/items/aaa2056aac0c270ba7d2 anzuzeigen

** Erstellen Sie ein Regressionsbaummodell, das den Preis eines Hauses anhand der 13 erklärenden Variablen vorhersagt, die das Haus charakterisieren. ** ** **

Konvertieren Sie zunächst 13 erklärende Variablen in einen Datenrahmen.

#Speichern Sie erklärende Variablen in DataFrame
boston = pd.DataFrame(boston_dataset.data, columns=boston_dataset.feature_names)

print(boston.head()) #Zeigen Sie die ersten 5 Zeilen an
print(boston.columns) #Spaltennamen anzeigen
print(boston.shape) #Überprüfen Sie die Form

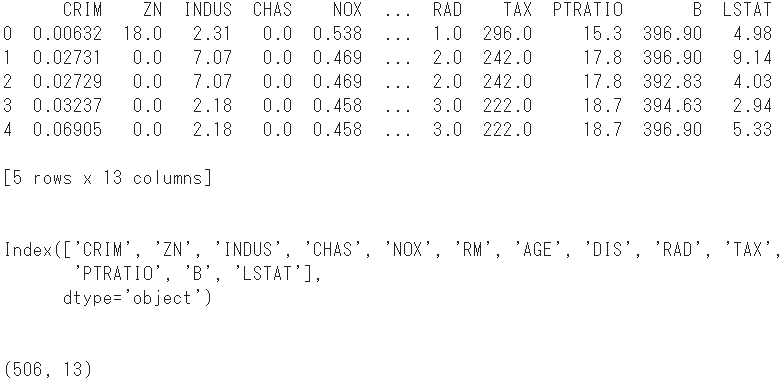
Fügen Sie dort die Zielvariable als Spaltennamen MEDV hinzu.

#Zielvariable hinzufügen
boston['MEDV'] = boston_dataset.target

print(boston.head()) #Zeigen Sie die ersten 5 Zeilen an
print(boston.shape) #Bestätigen Sie die Form erneut

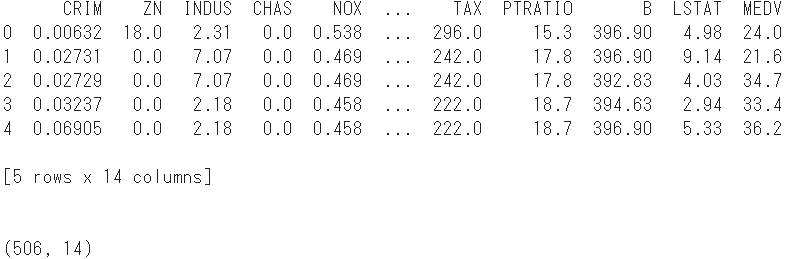
Die Anzahl der Stichproben beträgt 14 Spalten, indem die Zielvariable zu den erklärenden Variablen von 506 und 13 hinzugefügt wird.
Teilen Sie diesen Datensatz zufällig in zwei Gruppen ein, einen Trainingsdatensatz und einen Testdatensatz.

⑶ Datenaufteilung

#Konvertieren Sie das Dataset in ein Numpy-Array
array = boston.values

#Teilen Sie in erklärende Variablen und objektive Variablen
X = array[:,0:13]
Y = array[:,13]

70% der Daten werden als Trainingsdaten und die restlichen 30% als Testdaten verwendet.

#Importieren Sie ein Modul, das Daten aufteilt
from sklearn.model_selection import train_test_split

#Daten teilen
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=1234)

⑷ Konstruktion eines Regressionsbaummodells

Wie beim Klassifizierungsbaum wird die "Fit" -Methode durch Übergeben der Arrays X und Y trainiert, aber in diesem Fall ist Y vom numerischen Typ.
Das optionale max_leaf_nodes gibt an, wie viel der Baum wachsen wird. Hier beträgt die maximale Anzahl von Blattknoten 20.

#Modellinstanziierung
reg = DecisionTreeRegressor(max_leaf_nodes = 20)

#Modellgenerierung durch Lernen
model = reg.fit(X_train, Y_train)
print(model)

⑸ Bewertung des Regressionsbaummodells

Das erhaltene Regressionsbaummodell wird aus zwei Richtungen getestet: der Gültigkeit der Vorhersage (➀) und der Vielseitigkeit des Modells selbst (➁).
Um die Gültigkeit der Vorhersage zu bestätigen, wird zunächst zufällig aus 506 Stichproben ausgewählt und der aus der Merkmalsmenge vorhergesagte Preis mit dem tatsächlich beobachteten Preis verglichen.

➀ Bestätigen Sie die Gültigkeit der Vorhersage

Ruft zufällig nur eine ID aus dem Originaldatensatz X ab.

#Importieren Sie das Python-Standard-Pseudozufallszahlenmodul
import random
random.seed(1)

#Wählen Sie die ID nach dem Zufallsprinzip aus
id = random.randrange(0, X.shape[0], 1)
print(id)

#Extrahieren Sie die relevante Probe aus dem Originaldatensatz
x = X[id]
x = x.reshape(1,13)

#Prognostizieren Sie die Immobilienpreise anhand erklärender Variablen
YHat = model.predict(x)

#Konvertieren Sie die erklärende Variable der ID in DataFrame
df = pd.DataFrame(x, columns = boston_dataset.feature_names)
#Vorhersagewert y hinzugefügt
df["Predicted Price"] = YHat

Holen Sie sich die tatsächlich beobachteten Immobilienpreise und vergleichen Sie sie.

boston.iloc[id]

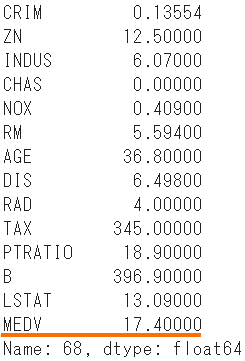
Der erwartete Preis beträgt 20,45, verglichen mit dem tatsächlichen Preis von 17,40.
Die nächste Überprüfung ist, inwieweit der vorhergesagte Wert des Modells die Informationsmenge des beobachteten Werts erklären kann.

➁ Überprüfen Sie den Entscheidungskoeffizienten als Index für die Vielseitigkeit

Der Entscheidungskoeffizient $ R ^ 2 $ ist ein Index, der die Erklärungskraft des vorhergesagten Werts $ \ hat {y} $ für den beobachteten Wert $ y $ in der Regressionsanalyse ausdrückt und auch als Beitragssatz bezeichnet wird.
Nimmt einen Wert von 0 bis 1 an und je näher $ R ^ 2 $ an 1 liegt, desto gültiger ist das Modell.

#Importieren Sie die Funktion zur Berechnung des Entscheidungskoeffizienten
from sklearn.metrics import r2_score

Übergeben Sie die erklärende Variable zum Testen (X_test) an das Modell, um den vorhergesagten Wert zu berechnen.

YHat = model.predict(X_test)

Übergeben Sie diese vorhergesagten Werte und die Zielvariable zum Testen (Y_test), um den Entscheidungsfaktor zu berechnen.

r2 = r2_score(Y_test, YHat)
print("R^2 = ", r2)

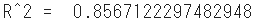
Die Anpassung des Modells an die Testdaten beträgt 0,86, was ein gutes Ergebnis ist.

⑹ Visualisierung des Regressionsbaummodells

#Importieren Sie das sklearn-Baummodul
from sklearn import tree

#Modul zum Anzeigen von Bildern in Notebook
from IPython.display import Image

#Modul zur Visualisierung des Entscheidungsbaummodells
import pydotplus

#Konvertieren Sie das Entscheidungsbaummodell in DOT-Daten
dot_data = tree.export_graphviz(model,
                                out_file = None,
                                feature_names = boston_dataset.feature_names,
                                class_names = 'MEDV',
                                filled = True)

#Zeichnen Sie ein Diagramm
graph = pydotplus.graph_from_dot_data(dot_data)  

#Diagramm anzeigen
Image(graph.create_png())

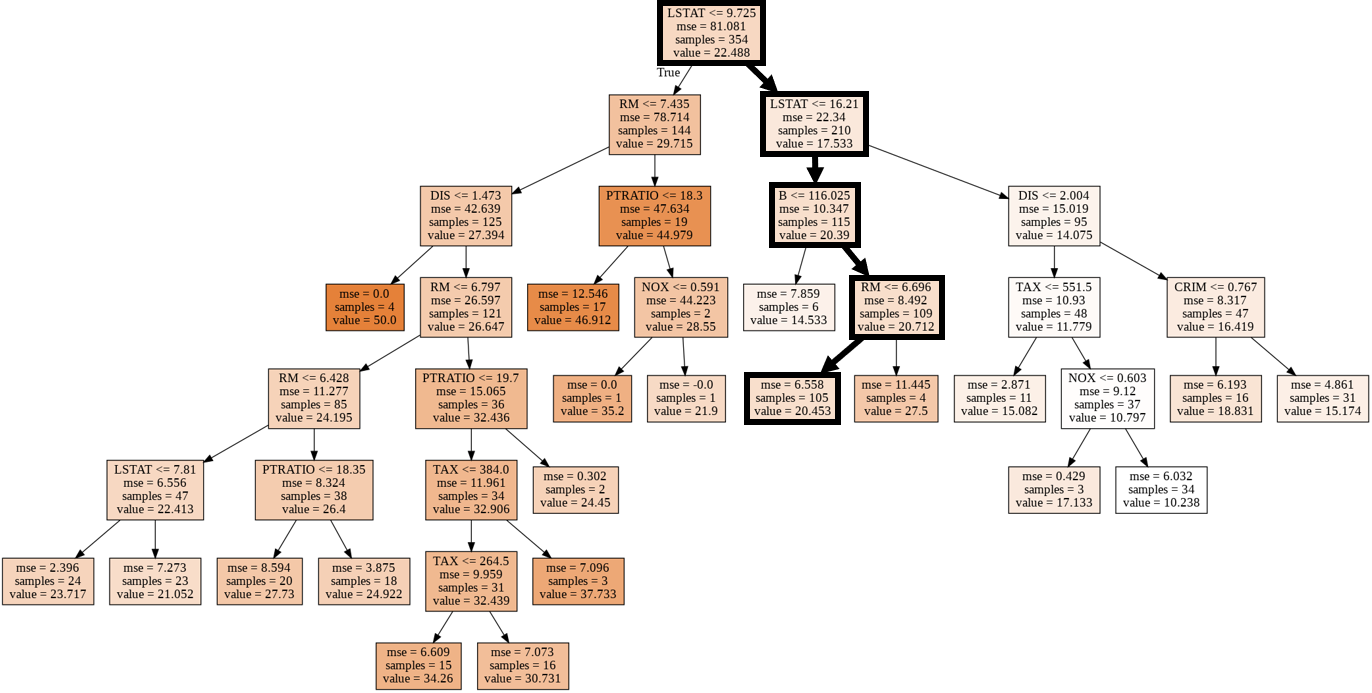
Die Route der zufällig extrahierten Probe (ID: 68) wird durch eine dicke Linie angezeigt.
Die Merkmalsmenge "LSTAT" des übergeordneten Knotens und des untergeordneten Knotens der ersten Schicht ist übrigens eine Abkürzung für "niedrigerer Status" und bedeutet das Verhältnis der unteren Klasse zur Bevölkerung.