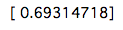Ich habe versucht, Couseras logistische Regression in Python zu implementieren

Cousera - Ich habe die logistische Regression von Dr. Andrew Ngs Machine3 Week3 implementiert. Ich habe versucht, so viel wie möglich nur numpy zu verwenden.

Die übliche Magie.

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

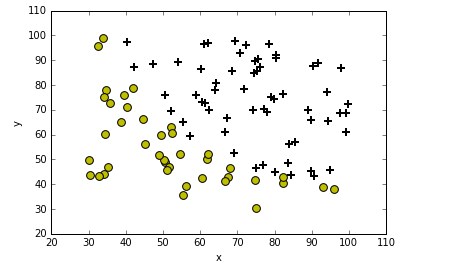
Lesen Sie die Daten und zeichnen Sie sie auf.

def plotData(data):
    neg = data[:,2] == 0
    pos = data[:,2] == 1

    plt.scatter(data[pos][:,0], data[pos][:,1], marker='+', c='k', s=60, linewidth=2)
    plt.scatter(data[neg][:,0], data[neg][:,1], c='y', s=60)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend(frameon= True, fancybox = True)
    plt.show()


data = np.loadtxt('ex2data1.txt', delimiter=',')
plotData(data)

Als nächstes Implementierung der Kostenfunktion und der Sigmoidfunktion

h_θ(x)=g(θ^Tx)

g(z)= \frac{1}{1+e^{-z}}

Sigmaid-Funktion

j(θ)= \frac{1}{m}(log(g(Xθ))^Ty+(log(1-g(Xθ))^T(1-y)))

Kostenfunktion

def sigmoid(z):
    return(1 / (1 + np.exp(-z)))

def CostFunction(theta, X, y):
    m = len(y)
    h = sigmoid(X.dot(theta))
    
    j = -1*(1/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y))
    
    return j

Schauen wir uns die ersten Kosten an.

X = np.c_[np.ones((data.shape[0],1)), data[:,0:2]]
y = np.c_[data[:,2]]

initial_theta = np.zeros(X.shape[1])
cost = CostFunction(initial_theta, X, y)
print(cost)

Die Kosten sind so. Als nächstes folgt die Implementierung der Methode mit dem steilsten Abstieg.

def gradient_decent (theta, X, y, alpha = 0.001, num_iters = 100000):
    m = len(y)
    history = np.zeros(num_iters)
    
    for inter in np.arange(num_iters):
        h = sigmoid(X.dot(theta))
        theta = theta - alpha *(1/m)*(X.T.dot(h-y))
        history[inter] = CostFunction(theta,X,y)

    return(theta, history)
    
initial_theta = np.zeros(X.shape[1])
theta = initial_theta.reshape(-1,1)
cost = CostFunction(initial_theta,X,y)
theta, Cost_h= gradient_decent(theta, X, y)

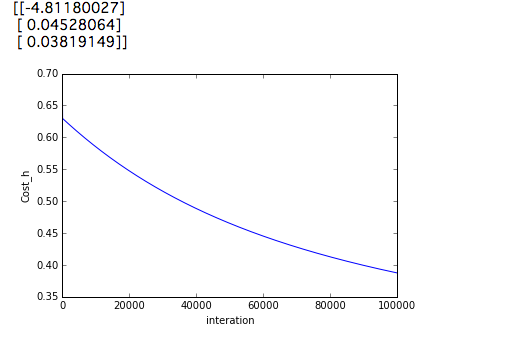
print(theta)
plt.plot(Cost_h)
plt.ylabel('Cost_h')
plt.xlabel('interation')
plt.show()

Das Ergebnis der Ausführung ist wie folgt.

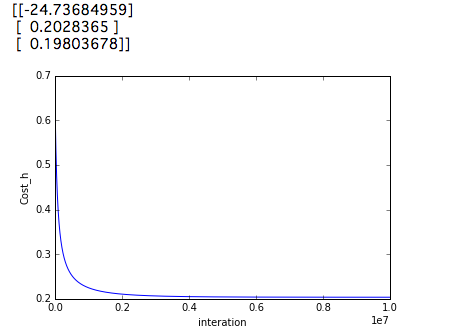
Aus irgendeinem Grund führt dies zu besseren Ergebnissen als das Setzen von num_iters auf 10000000. Mal sehen, das Ergebnis.

def predict(theta, X, threshold = 0.5):
    p = sigmoid(X.dot(theta)) >= threshold
    
    return(p.astype('int'))

p = predict(theta,X)
y = y.astype('int')

accuracy_cnt = 0
for i in range(len(y)):
    if p[i,0] == y[i,0]:
        accuracy_cnt +=1

print(accuracy_cnt/len(y) * 100)

Wenn Sie den obigen Code ausführen, erhalten Sie 91,0%. Was ist, wenn Sie num_inter bei 1000000 ausführen? ..

Wenn Sie diese Genauigkeit überprüfen, beträgt sie 89,0%. Es ist unklar, warum die oben genannten Ergebnisse trotz der geringeren Kosten schlechter sind.