Implementierte Perceptron-Lernregeln in Python
Über diesen Beitrag
Ich habe Perceptrons Lernregel, eine der Methoden zum Bestimmen der Unterscheidungsgrenze für linear trennbare Datengruppen, in Python ohne Verwendung einer Bibliothek implementiert. Ich bin ein Anfänger sowohl in Python als auch im maschinellen Lernen. Bitte weisen Sie auf schlechte Punkte hin.
Für "Widrow-Hoff-Lernregeln", die neben "Perceptron-Lernregeln" verglichen werden, ["Implementieren von Widrow-Hoff-Lernregeln in Python"](http: / /qiita.com/s-kiriki/items/6a90beede4c139558bcc).
Perceptrons Theorie der Lernregeln
Die Umrisse und Formeln der Lernregeln von Perceptron sind in der folgenden Folie (ab der Mitte der Folie) grob zusammengefasst.
https://speakerdeck.com/kirikisinya/xin-zhe-renaiprmlmian-qiang-hui-at-ban-zang-men-number-2
Implementierung
Für eine Dimension
Finden Sie die Trennungsgrenze von linear trennbaren Trainingsdaten, die in einer Dimension vorhanden sind (siehe Abbildung unten) und zu einer der beiden Klassen gehören.

Als Umsetzungspunkt
- Der anfängliche Gewichtsvektor ist "w = (0,2,0,3)" und der Lernkoeffizient ist "ρ = 0,5".
- Wir haben die Konvergenz der Trennungsgrenze nicht beurteilt und die Korrektur (Lernen) des Gewichtsvektors ausreichend oft (100 Mal) wiederholt (ich denke, es ist nicht wirklich gut, aber ich dachte, es wäre gut, die Maschine viel Arbeit machen zu lassen. .)
Der eigentliche Code sieht folgendermaßen aus:
# coding: UTF-8
#Implementierungsbeispiel für eine eindimensionale Perceptron-Lernregel
import numpy as np
import matplotlib.pyplot as plt
def train(wvec, xvec, is_c1):
low = 0.5#Lernkoeffizient
if (np.dot(wvec,xvec) > 0) != is_c1:
if is_c1:
wvec_new = wvec + low*xvec
else:
wvec_new = wvec - low*xvec
return wvec_new
else:
return wvec
if __name__ == '__main__':
data = np.array([[1.0, 1],[0.5, 1],[-0.2, 2],[-1.3, 2]])#Datengruppe
features = data[:,0].reshape(data[:,0].size,1)#Merkmalsvektor
labels = data[:,1]#Klasse (diesmal c1=1,c2=2)
wvec = np.array([0.2, 0.3])#Anfangsgewichtsvektor
is_c1s = (labels == 1)#Ein Array von c1 oder boolean
xvecs = np.c_[np.ones(features.size), features]#xvec[0] = 1
loop = 100
for j in range(loop):
for xvec, is_c1 in zip(xvecs, is_c1s):
wvec = train(wvec, xvec, is_c1)
print wvec
print -(wvec[0]/wvec[1])
#Diagrammdarstellung
plt.axhline(y=0, c='gray')
plt.scatter(features[is_c1s], np.zeros(features[is_c1s].size), c='red', marker="o")
plt.scatter(features[~is_c1s], np.zeros(features[~is_c1s].size), c='yellow', marker="o")
#Trennungsgrenze
plt.axvline(x=-(wvec[0]/wvec[1]), c='green')
plt.show()
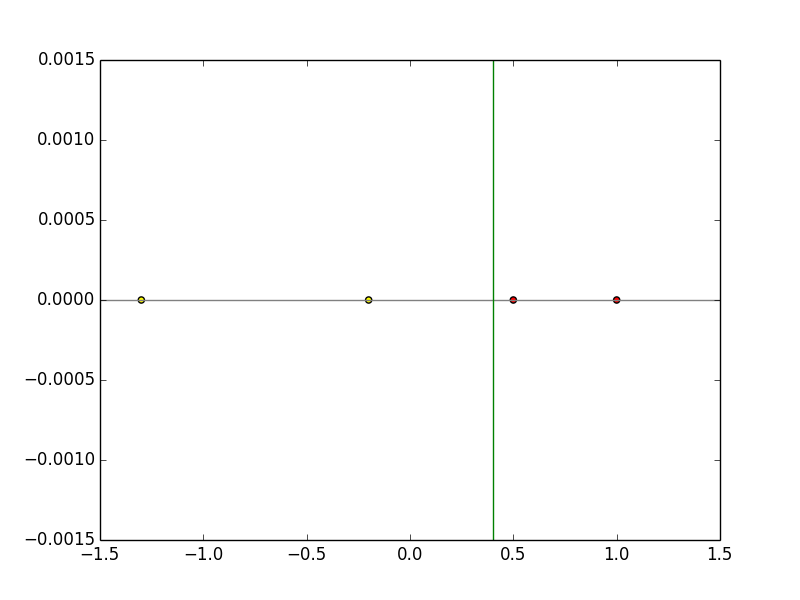
Der Gewichtsvektor nach dem Training ist "w = (-0,3, 0,75)". Wenn dies in die Formel "wx = 0" eingesetzt wird, wird die Diskriminanzfunktion zu "x = 0,4", und es ist ersichtlich, dass die lineare Trennung erfolgreich durch Lernen durchgeführt wird, wie in der folgenden Abbildung gezeigt.
Bei 2 Dimensionen
Wie in der folgenden Abbildung (Bild) gezeigt, finden Sie die Trennungsgrenzlinie linear trennbarer Trainingsdaten, die in zwei Dimensionen vorhanden sind und zu einer der beiden Klassen gehören.

Als Umsetzungspunkt
- Verwenden Sie
np.random.rand, um zwei Klassen linear trennbarer Daten zu generieren - Der anfängliche Gewichtsvektor ist "w = (2, -1,3)" und der Lernkoeffizient ist "ρ = 0,5".
- Wie im Fall einer Dimension wurde die Konvergenz der Trenngrenze nicht beurteilt, und die Korrektur (Lernen) des Gewichtsvektors wurde ausreichend oft (100 Mal) wiederholt.
Der eigentliche Code sieht folgendermaßen aus:
# coding: UTF-8
#Implementierungsbeispiel für eine 2D-Perceptron-Lernregel
import numpy as np
import matplotlib.pyplot as plt
import sys
def train(wvec, xvec, label):
low = 0.5#Lernkoeffizient
if (np.dot(wvec,xvec) * label < 0):
wvec_new = wvec + label*low*xvec
return wvec_new
else:
return wvec
if __name__ == '__main__':
train_num = 100#Anzahl der Trainingsdaten
#Trainingsdaten der Klasse 1
x1_1=np.random.rand(train_num/2) * 5 + 1 #x Komponente
x1_2=np.random.rand(int(train_num/2)) * 5 + 1 #y-Komponente
label_x1 = np.ones(train_num/2) #Etikett (alle 1)
#Trainingsdaten der Klasse 2
x2_1=(np.random.rand(train_num/2) * 5 + 1) * -1 #x Komponente
x2_2=(np.random.rand(train_num/2) * 5 + 1) * -1 #y-Komponente
label_x2 = np.ones(train_num/2) * -1 #Etiketten (alle-1)
x0=np.ones(train_num/2) #x0 ist immer 1
x1=np.c_[x0, x1_1, x1_2]
x2=np.c_[x0, x2_1, x2_2]
xvecs=np.r_[x1, x2]
labels = np.r_[label_x1, label_x2]
wvec = np.array([2,-1,3])#Anfangsgewichtsvektor Entsprechend bestimmen
loop = 100
for j in range(loop):
for xvec, label in zip(xvecs, labels):
wvec = train(wvec, xvec, label)
print wvec
plt.scatter(x1[:,1], x1[:,2], c='red', marker="o")
plt.scatter(x2[:,1], x2[:,2], c='yellow', marker="o")
#Trennungsgrenze
x_fig = np.array(range(-8,8))
y_fig = -(wvec[1]/wvec[2])*x_fig - (wvec[0]/wvec[2])
plt.plot(x_fig,y_fig)
plt.show()
Da die Trainingsdaten zufällig generiert werden, unterscheiden sich der Gewichtsvektor und die Unterscheidungsfunktion nach dem Training jedes Mal. Als Beispiel für das tatsächliche Ausführungsergebnis ist es in der folgenden Abbildung dargestellt, und es ist ersichtlich, dass die lineare Trennung durch Lernen erfolgreich durchgeführt wird.

Recommended Posts