[PYTHON] Vorhersage von Zeitreihendaten mit einem neuronalen Netzwerk
Verwenden Sie beim Umgang mit Zeitreihendaten in einem neuronalen Netzwerk ein wiederkehrendes neuronales Netzwerk. Dieses Mal werde ich das wiederkehrende neuronale Netzwerk erklären.
(Da es lang ist, wird das neuronale Netzwerk als NN und das wiederkehrende neuronale Netzwerk als RNN abgekürzt.)
Übersicht über RNN
In einigen Daten haben die vorherigen Daten eine Korrelation mit den nächsten Daten, z. B. wenn ein "x" erscheint, besteht eine hohe Wahrscheinlichkeit, dass ein "y" kommt. Insbesondere ist es so etwas wie Wörter oder Musik (wie "ha" oder "ga" kommt oft nach "I"). Für solche zeitreihenkorrelierten Daten ist es natürlich verlockend, zuvor generierte Daten zu berücksichtigen. Ist es möglich, zuvor generierte Daten in NN einzugeben? Die Antwort lautet RNN.
Insbesondere ist es wie in der folgenden Abbildung gezeigt.

Der Inhalt der verborgenen Ebene zum Zeitpunkt $ t $ wird beim nächsten Mal $ t + 1 $ als Eingabe behandelt. Die verborgene Ebene von $ t + 1 $ wird mit $ t + 2 $ ... fortgesetzt, aber der Punkt ist, dass die vorherige verborgene Ebene auch zum Lernen der nächsten verborgenen Ebene verwendet wird.
RNN-Typ
| Name | Kombiniertes Ziel | Charakteristisch |
|---|---|---|
| Fully recurrent network | Alle Knoten(1:N) | Kombinieren Sie vollständig bidirektional, einschließlich sich selbst |
| Hopfield network | Alle Knoten(1:N-1) | Bidirektionaler Join, schließt sich nicht in das Join-Ziel ein |
| Elman network | 1:1 (Versteckte Ebene->Versteckte Ebene) | Eingabeebene / Kontext(Versteckte Ebene)・ Dreischichtige Struktur der Ausgabeschicht |
| Jordan network | 1:1 (Ausgabeschicht->Versteckte Ebene) | Eingabeebene / Kontext(Versteckte Ebene)・Ausgabeschichtの3層構造 |
| Echo state network (ESN) | 1->1? | Das Ziel der Verbindung ist eine Reihe von Knoten(reservoir)Zufällig bestimmt aus |
| Long short term memory network (LSTM) | - | Anstelle des RNN-Knotens wird ein Block verwendet, der den Eingabewert enthalten kann. Hohe Präzision |
| Bi-directional RNN (BRNN) | - | Bidirektional(Vergangenheit->Zukunft/Zukunft->Vergangenheit)Eine Kombination von RNNs |
Hopfield-Netzwerk hat anwendbar auf Optimierungsprobleme zusätzlich zur allgemeinen Klassifizierung. /~kanakubo/research/neuro/hopfieldnetwork.html) Dies ist ein Modell.
Elman / Jordan ist die einfachste Form (wie es heißt, einfache wiederkehrende Netzwerke) (http://en.wikipedia.org/wiki/Types_of_artificial_neural_networks#Simple_recurrent_networks). Wenn Sie RNN verwenden möchten, versuchen Sie es zuerst. Wenn bei der Genauigkeit ein Problem auftritt, wechseln Sie zu einer anderen Methode. Der Unterschied zwischen Elman / Jordan ist wie oben (unabhängig davon, ob die vorherigen Daten von der verborgenen Schicht oder der Ausgabeschicht wiedergegeben werden), jedoch hier. Es ist auch ausführlich in geschrieben. Es gibt keinen genauen Vorteil, aber ich denke, Elman ist flexibler, da die Menge der nächsten Ausbreitung abhängig von der Anzahl der verborgenen Schichten geändert werden kann.
Echo State Network ist ein Modell mit unterschiedlicher Haarfarbe, und die Knoten werden nicht im Voraus kombiniert und in einem Pool namens Reservoir (dh Reservoir usw.) gespeichert. Es ist ein Stil, der sich nach der Eingabe zufällig / dynamisch verbindet. Der Punkt ist, dass es im menschlichen Gehirn keine vorgegebene Verbindung gibt, daher wurde sie mit dem Konzept geschaffen, sie zu imitieren und fließend zu verbinden. Es scheint, dass dies auch als Liquid State Machines (wörtlich: Flüssigkeitsmechanismus) bezeichnet wird.
Langzeit-Kurzzeitgedächtnisnetzwerk (LSTM) und bidirektionales RNN (BRNN) unterliegen keinen besonderen Einschränkungen hinsichtlich des Beitritts. LSTM verwendet einen LSTM-Block, der sich Gewichte anstelle einfacher Knoten merken kann. Dies dient zur Lösung der Lernherausforderungen in RNN und wird später erläutert.
Bidirektionales RNN kann die Genauigkeit verbessern, indem es nicht nur in eine Richtung von Vergangenheit zu Zukunft lernt, sondern auch Zeitreihen in einer bestimmten negativen Richtung von Zukunft zu Vergangenheit lernt.
RNN lernen
Die folgenden Dokumente sind sehr sorgfältig über das Erlernen von RNN geschrieben. Obwohl es auf Englisch ist, gibt es zu diesem Zeitpunkt (2015/1) fast keine japanische Literatur zu RNN, so dass es keine andere Wahl gibt, als aufzugeben und es zu lesen.
Das RNN-Lernen konvergiert im Allgemeinen nur sehr langsam. Sie müssen die Lernrate für die Genauigkeit verringern, aber wenn Sie sie verringern, wird die bereits langsame Konvergenz verlangsamt. Dies ist ein Kompromiss, aber es scheint eine Möglichkeit zu geben, ihn zu lösen, indem die Gradienteninstabilität im Optimierungsprozess berücksichtigt wird (Einzelheiten finden Sie unter [EFFIZIENTE LERNALGORITHMEN ZWEITER ORDNUNG FÜR NEUHEITLICHE NETZWERKE IM DISKRETEN ZEITRAUM]]. (Siehe http://ir.nmu.org.ua/bitstream/handle/123456789/120274/866d31771b48ba40c56fcc039f091b9b.pdf?sequence=1&isAllowed=y#page=58).
Eine Sache, die ich sagen kann, ist, dass es derzeit (2015/1) keine etablierte Methode gibt, die keine Probleme mit Genauigkeit und Geschwindigkeit beim RNN-Lernen hat. Daher gibt es natürlich keine Bibliothek, die dies implementiert. .. Hier muss man stetig üben.
BPTT (BackPropagation Through Time) Die Grundidee ist, dass die Backpropagation wie gewohnt anwendbar sein sollte, da RNNs beim Erweitern als lange NNs betrachtet werden können. Das Bild ist wie folgt.

Der Fehler breitet sich vom letzten Mal T zur ersten 0 aus. Daher ist der Fehler der Ausgabeschicht zu einem bestimmten Zeitpunkt t die Summe aus "der Differenz zwischen Lehrer (Lehrerdaten) und Ausgabe (Ausgabe) zum Zeitpunkt t" und "dem von t + 1 übertragenen Fehler".
Wie aus der Abbildung hervorgeht, kann BPTT nicht ohne die Daten bis zum letzten T, dh allen Zeitreihendaten, trainieren. Daher müssen Maßnahmen ergriffen werden, z. B. nur die neuesten Daten für lange Daten herauszuschneiden.
Dieses BPTT weist verschiedene Probleme auf, und es wurden verschiedene Lernmethoden entwickelt, um diese zu lösen.
LSTM(Long short term memory) Wenn T zu groß ist, dh für lange Zeitreihendaten, kann der Fehler aus der oberen Schicht aufgrund eines Berechnungsproblems verringert oder umgekehrt sehr groß sein (dies wird hier detailliert beschrieben (p8 ~)]( http://www.slideshare.net/beam2d/pfi-seminar-20141030rnn)). Wenn der Wert zunimmt, ist der Maximalwert begrenzt, aber es kann nicht geholfen werden, ihn zu verschwinden. Daher besteht die Idee von LSTM darin, den Fehler so zu verbreiten, dass er nicht abfällt.
teacher forcing In RNN wird die Ausgabe von t zur Eingabe von t + 1 usw., aber zum Zeitpunkt des Lernens ist die korrekte Antwort der Eingabe auf t + 1 für den Lehrer klar, also die Methode, sie so zu verwenden, wie sie ist ist. Dies macht es möglich, jede Schicht zu trainieren, wobei der Einfluss der unteren Schicht ignoriert und die Konvergenzgeschwindigkeit erhöht wird, aber es scheint, dass die Ausgabe nicht stabil ist, wenn sie tatsächlich ausgeführt wird (nach dem Lernen).
RPROP(Resilient backpropagation) Dies ist die Methode, die auch für reguläre NNs verwendet wird. Beim Training von NN wird der Gradient berechnet und das Gewicht ($ \ eta $) damit multipliziert, wie sich die Richtung (Vorzeichen) des Gradienten zwischen dem letzten Mal und jetzt geändert hat (siehe [hier](http für Details). Sie können mehr über //paginas.fe.up.pt/~ee02162/dissertacao/RPROP%20paper.pdf) lesen.
- Wenn das Vorzeichen zwischen dem vorherigen und diesem Zeitpunkt gleich ist, wird das Lernen durch Gewichtung des Gradienten beschleunigt.
- Wenn sich das Vorzeichen zwischen dem vorherigen und diesem Zeitpunkt unterscheidet, wird der Gradient abgebremst und die Lösung kehrt zur übersehenen optimalen Lösung zurück.
Ich denke, es heißt Resilient, weil sich dieses Verhalten wie das Rollen eines Balls anfühlt (Beschleunigen auf einem Gefälle, Verlangsamen, wenn das Gefälle die Richtung ändert und Ausüben einer Kraft in die entgegengesetzte Richtung). ..
Mit einer Funktion wie der Sigmoid-Funktion wird das Lernen schwierig, da es flach ist (Gradient ist fast 0), wenn der Wert einen bestimmten Bereich überschreitet (Flat Spot Problem. wiki / Flat_Spot_Problem)))) Die Anwendung dieser Methode verhindert auch eine Lernstagnation aufgrund des Gewichts.
Es gibt viele Variationen dieser Technik. Weitere Informationen finden Sie unter hier.
Zusätzlich zu den verschiedenen oben beschriebenen Methoden ist es auch wichtig, Parameter wie die Lernrate, die den Grad der Fehlerausbreitung anpasst, und den Impuls, der den Einfluss der vorherigen Schicht anpasst, wie bei normalem NN einzustellen.
BPTT konvergiert im Allgemeinen nur langsam und das Erlernen dauert lange. Daher werden Knoten mit versteckten Schichten häufig in kleinen Netzwerken von etwa 3 bis 20 verwendet, und wenn dies überschritten wird, kann das Lernen mehrere Stunden oder sogar länger dauern.
RTRL (Real Time Recurrent Learning) Im Gegensatz zu BPTT ist RTRL eine Methode zur zukünftigen Verbreitung von Fehlern, die es für das Online-Lernen geeignet macht.

Aktualisiert das Gewicht beim nächsten Mal t + 1 mit dem Fehler, der zum Zeitpunkt t aufgetreten ist. In der obigen Abbildung wird der Fehler zu jedem Zeitpunkt berechnet und weitergegeben, es gibt jedoch auch eine Methode zum Aktualisieren nach einem bestimmten Zeitraum (Epoche). Da jedoch das Gewicht, das auf einmal aktualisiert werden muss, größer als das von BPTT ist, ist die Berechnungslast hoch.
EKF (Extended Kalman Filter) Es ist EKF, das den erweiterten Kalman-Filter auf RNN anwendet und das Gewicht aktualisiert. Das erweiterte Kalman-Filter ist eine nichtlineare Erweiterung des Kalman-Filters, das lineare Systeme verarbeitet und den Status des Systems wie folgt schätzt.
$ x(n+1) = f(x(n)) + q(n) $ $ d(n) = h_n(x(n)) $
Die obige Formel drückt das Folgende aus.
- Der nächste Zustand $ x (n + 1) $ repräsentiert die Eingabe $ f (x (n)) $ aus dem vorherigen Zustand $ x (n) $ und $ q (n) $ (externes Rauschen) Wird bestimmt durch
- Die Ausgabe des Zustands $ x (n) $ ist $ h_n (x (n)) $
Das Bild ist in der folgenden Abbildung dargestellt.

Und RNN kann als dieser erweiterte Kalman-Filter angesehen werden. Die folgende Abbildung zeigt dies.
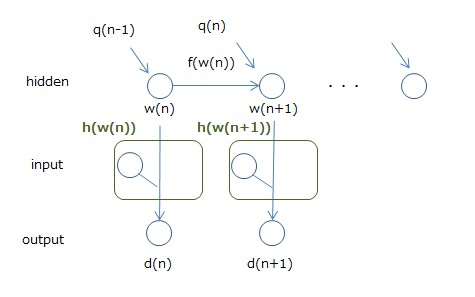
Ich denke, es ist in Ordnung, das Gewicht $ w $ als Zustand und die Ausgabe als $ d $ zu haben. Das Problem ist die Eingabe, aber wenn wir sie als Teil der Funktion $ h $ zur Berechnung der Ausgabe $ d $ betrachten, sagen wir, dass es sich um einen erweiterten Kalman-Filter handelt (tatsächlich die Eingabe und die Gewichte der Eingabe). Es wird in $ w $ berechnet, daher denke ich nicht, dass es zu schwierig ist.
Dann kann das Verfahren zum Aktualisieren des Zustands des erweiterten Kalman-Filters angewendet werden, ebenso wie das Aktualisieren des Zustands von RNN, dh des Gewichts. Die Formel zum Aktualisieren des Status ist ziemlich kompliziert, daher werde ich die Details weglassen, aber die Methode namens EKF bringt die Methode des erweiterten Kalman-Filters auf diese Weise zu RNN. Es gibt auch eine Methode zur Vereinfachung der Berechnung, die vielversprechend ist. Wie bei BPTT und RTRL ist jedoch eine empirische Abstimmung (Lernrate, Netzwerkkonfiguration usw.) erforderlich, um Genauigkeit zu erzielen.
RNN-Bibliothek
Pybrain wird eindeutig von großen Bibliotheken unterstützt. Ein Tutorial für wiederkehrende Netzwerke (http://pybrain.org/docs/tutorial/netmodcon.html#using-recurrent-networks) ist ebenfalls verfügbar.
Es scheint, dass es mit pylearn2 möglich ist, das für Deep Learning bekannt ist, aber wie Sie auf dem Pfad sehen können, befindet es sich derzeit (2015/1) noch im Sandkasten und es ist in einem unangenehmen Zustand, es tatsächlich zu verwenden.
lisa-lab/pylearn2 pylearn2/pylearn2/sandbox/rnn/models/tests/test_rnn.py
Wenn Sie es selbst implementieren möchten, wird die Methode mit Theano eingeführt.
Implementing a recurrent neural network in python gwtaylor/theano-rnn
Dies ist eine Kombination aus RNN und RBM, aber die Implementierung einschließlich des Codes wird eingeführt.
Modeling and generating sequences of polyphonic music with the RNN-RBM Einführung in die Vorhersage und Erzeugung von Melodien durch RNN-RBM und die Verarbeitung von Musikinformationen
Darüber hinaus scheint neuraltalk ein Modell zu sein, das ein Bild und seine Erklärung trainiert und eine Erklärung ausgibt, wenn ein Bild gegeben wird. Es ist eher eine fertige als eine Bibliothek zum Bauen, aber ich denke, es ist gut, sie für diesen Zweck zu verwenden.
RNN-Implementierung
Dieses Mal werde ich RNN mit "pybrain" implementieren, das ein Implementierungsbeispiel wie oben beschrieben enthält.
Die neueste Version von PyBrain ist 0.3.3 (Stand Januar 2015). Es scheint, dass es auf die PYPI-Site hochgeladen wurde (https://pypi.python.org/pypi/PyBrain/0.3.3) ... aber da es 0.3.2 ist, von pip einzugeben, git clone Löschen Sie das Repository mit und installieren Sie es. Die Vorgehensweise und die abhängigen Bibliotheken finden Sie hier.
Die Hauptabhängigkeit ist Scipy. Python ist als 2.5 geschrieben, aber ich habe bestätigt, dass der Test (python runtests.py) mit Python 3.4.2 in meiner Umgebung bestanden werden kann. Wenn man sich das Problem usw. ansieht, scheint es, dass Python 3 in einigen Teilen nicht unterstützt wird, aber es gab kein Problem bei der Verwendung (es sei denn, es liegt ein Fehler vor, ohne es zu wissen ...).
Für die vorhergesagten Zeitreihendaten haben wir Balltrajektoriendaten generiert und verwendet. Ballgebundene Daten (www.cs.utoronto.ca/~ilya/code), die ursprünglich in [diesem Dokument] verwendet wurden (http://arxiv.org/ftp/arxiv/papers/1206/1206.6392.pdf) /2008/RTRBM.tar), aber die Betriebsumgebung ist alt wie Python2, und wenn Sie der Beschreibung in README glauben, wird das Lernen eine Woche dauern (Zitat: Die Probleme mit springenden Bällen trainieren für eine erheblich längere Anzahl von) Da es Zeit war (ungefähr eine Woche auf einem schnellen Computer ...)), beschloss ich, eine einfache Flugbahn zu generieren und zu verwenden.
Der Aufbau des Modells wird im PyBrain-Tutorial sorgfältig beschrieben, die wichtigsten Beschreibungsmethoden sind jedoch nachstehend zusammengefasst.
Welcome to PyBrain’s documentation!
Aufbau eines Netzwerks
Mit "pybrain.structure" zusammenbauen. Im Folgenden bauen wir ein normales Netzwerk mit einem Bias-Term in 2-3-1 auf.
Building Networks with Modules and Connections
from pybrain.structure import FeedForwardNetwork, LinearLayer, SigmoidLayer, BiasUnit, FullConnection
net = FeedForwardNetwork()
net.addInputModule(LinearLayer(2, name='i'))
net.addModule(BiasUnit('bias'))
net.addModule(SigmoidLayer(3, name='h'))
net.addOutputModule(LinearLayer(1, name='o'))
# connect nodes
net.addConnection(FullConnection(net['i'], net['h']))
net.addConnection(FullConnection(net['bias'], net['h']))
net.addConnection(FullConnection(net['bias'], net['o']))
net.addConnection(FullConnection(net['h'], net['o']))
Es ist einfacher, mit buildNetwork zu erstellen. Das Folgende ist das gleiche wie der obige Prozess.
net = buildNetwork(2, 3, 1, bias=True, hiddenclass=SigmoidLayer)
Das Netzwerk lernen
Bereiten Sie für das Training zunächst einen Datensatz vor. Im Folgenden werden die Daten von Ausgabe 1 gemäß dem oben aufgebauten Netzwerk als "addSample" an Eingabe 2 übergeben (Beachten Sie, dass "appendLinked" und "addSample" im Dokument äquivalent sind. //github.com/pybrain/pybrain/blob/1dd5086a51c3c98497ef85b31178588a89d8951e/pybrain/datasets/unsupervised.py#L31)).
from pybrain.datasets import SupervisedDataSet
ds = SupervisedDataSet(2, 1)
ds.addSample((0, 0), (0,))
...
Das Training wird anhand des vorbereiteten Datensatzes durchgeführt. training.train gibt ein doppeltes Verhältnis zum Fehler zurück, mit dem Sie die Anpassung an Ihre Trainingsdaten bewerten können.
Training your Network on your Dataset
from pybrain.supervised.trainers import BackpropTrainer
net = buildNetwork(2, 3, 1, bias=True, hiddenclass=TanhLayer)
trainer = BackpropTrainer(net, ds)
err = trainer.train()
Netzwerkvorhersage
Die Vorhersage erfolgt mit der Funktion "Aktivieren".
net.activate([1, 2])
Erstellen Sie RNN
Im Fall von RNN entspricht dies fast einem normalen Netzwerkaufbau. RNN verwendet "RecurrentNetwork" und stellt beim Herstellen einer rekursiven Verbindung eine Verbindung mit "addRecurrentConnection" her.
Dann wird die Vorhersage durch "Aktivieren" ausgeführt, nachdem sie einmal mit "net.reset ()" zurückgesetzt wurde. In Bezug auf "Aktivieren" habe ich im obigen Beispiel vorausgesagt, dass ich immer den gleichen Wert eingegeben habe, aber in Wirklichkeit war dies nicht der Fall, es sei denn, ich habe den vorhergesagten Wert erneut eingegeben und dies getan (theoretisch sogar die erste Eingabe). Wenn ja, kann es danach immer mehr vorhergesagt werden, so dass ich das Gefühl habe, dass es kein Problem gibt, selbst wenn der Anfangswert so bleibt, wie er ist ...).
Diesmal habe ich es mit Elman und Jordan versucht. Unten ist ein Bild in Jordanien. Die x- und y-Koordinaten und ihre jeweiligen Beschleunigungen werden als Eingaben übergeben.

Da die Beschleunigung durch die Position der Zeit t und die Position der Zeit t + 1 bestimmt wird, dachte ich, dass sie in der verborgenen Schicht gut lernen würde ... aber ich fügte sie als Eingabeparameter hinzu, weil sie nicht genau war.
Für die Trainingsdaten haben wir mehrere Chargen mit unterschiedlichen Ausgangspositionen bei gleicher Anfangsbeschleunigung vorbereitet und damit trainiert / getestet. Da die anfängliche Beschleunigung für die Trainings- / Testdaten gleich ist, ist dieses Modell ein Modell, das schätzt, welche Art von Flugbahn gezogen wird, wenn der Ball an einem bestimmten Punkt unter dieser Beschleunigung platziert wird.
Es ist eine interessante Genauigkeit, aber der Fehler mit den Testdaten betrug durchschnittlich etwa 5,7, was nicht sehr gut war. Da diese Daten die Flugbahn eines Balls vorhersagen, der in einem Quadrat von 10 x 10 springt, ist ein Fehler von 5,7 ein Wert, der als fast völlig falsch bezeichnet werden kann.
Obwohl es sich so weit bewegt, dass Sie das Gefühl in der Animation verstehen können, ist es viel für eine vollständige Reproduktion. Ich habe auch versucht, die verborgenen Ebenen und Knoten zu vergrößern oder zu verkleinern, aber es hat sich nicht geändert.
Tatsächliche Umlaufbahn
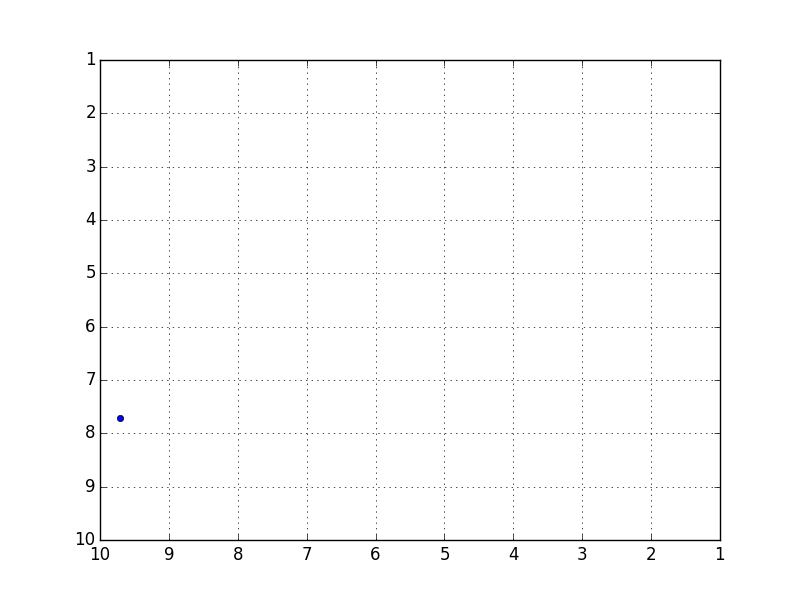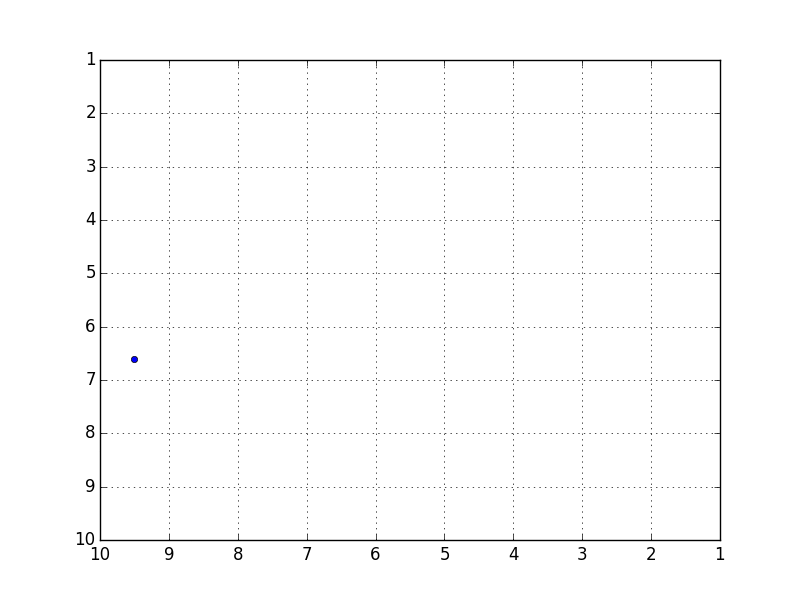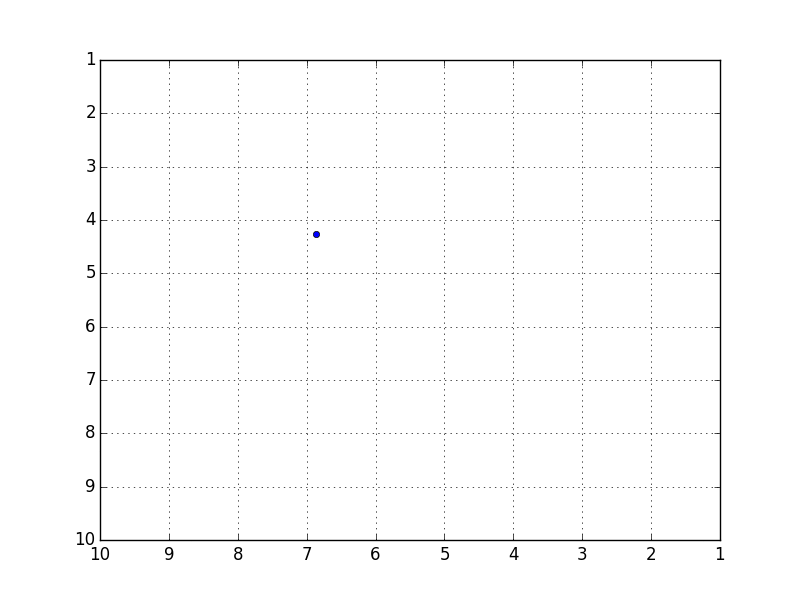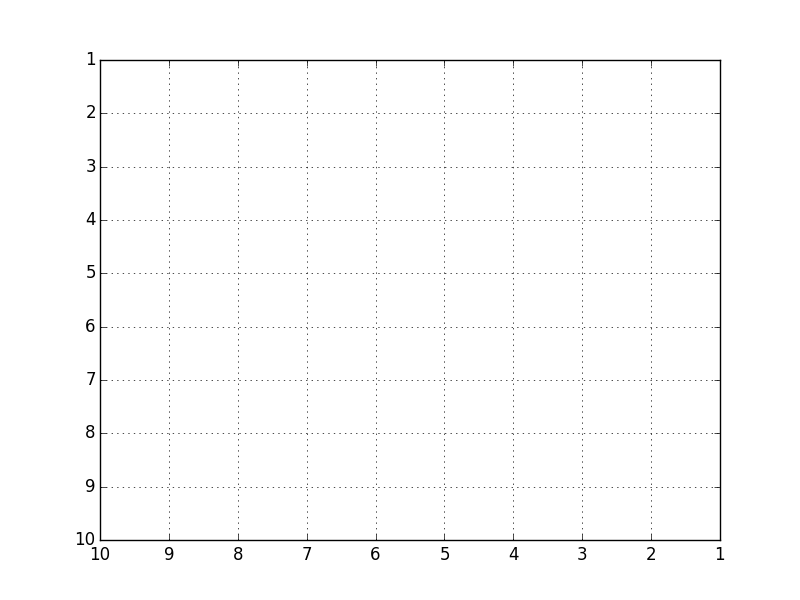
Voraussichtliche Flugbahn (ziemlich nahe an der besten)

Der zur Überprüfung verwendete Code ist hier. Wenn jemand sagt, dass ich es bin, warte ich auf eine Pull-Anfrage.
Referenz
- Über RNN
- Recurrent neural network
- Types of artificial neural networks
- Hopfield network
- Echo state network
- What is the difference between Elman and Jordan neural networks
- Recurrent Neural Networks
- Bidirectional recurrent neural networks
- A tutorial on training recurrent neural networks, covering BPPT, RTRL, EKF and the "echo state network" approach
- A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm
- Papiere zur RNN-Implementierung usw.
- Modeling and generating sequences of polyphonic music with the RNN-RBM
- Modeling Temporal Dependencies in High-Dimensional Sequences:Application to Polyphonic Music Generation and Transcription
- ↑ Artikel, der das Papier auf Japanisch erklärt [Einführung in die Vorhersage und Erzeugung von Melodien durch RNN-RBM und die Verarbeitung von Musikinformationen](http://xiangze.hatenablog.com/entry/2014/09/28/ 143934)
- Continuous time recurrent neural networks for grammatical induction
- Über PyBrain
- Welcome to PyBrain’s documentation!
Recommended Posts