google traduit http://scikit-learn.org/0.18/modules/outlier_detection.html [scikit-learn 0.18 Guide de l'utilisateur 2. Apprendre sans enseignant](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA À partir de% E3% 81% 97% E5% AD% A6% E7% BF% 92)

2.7. Détection de la nouveauté et des valeurs aberrantes

De nombreuses applications doivent être en mesure de déterminer si une nouvelle observation appartient à la même distribution (inlier) qu'une observation existante ou si elle est différente (outlier). Cette fonctionnalité est souvent utilisée pour effacer le jeu de données réel. Deux distinctions importantes doivent être faites:

** Détection de nouveauté: **
Les données d'entraînement ne sont pas polluées par des valeurs aberrantes, je suis donc intéressé par la détection d'anomalies avec de nouvelles observations.
** Détection des valeurs aberrantes: **
Les données d'entraînement contiennent des valeurs aberrantes et les observations d'écart doivent être ignorées pour s'insérer dans le mode central des données d'entraînement.

Le projet scikit-learn fournit un ensemble d'outils d'apprentissage automatique qui peuvent être utilisés à la fois pour la détection de nouveautés et de valeurs aberrantes. Cette stratégie est mise en œuvre avec des objets qui apprennent à partir des données sans surveillance.

estimator.fit(X_train)

Les nouvelles observations peuvent être classées comme valeurs aberrantes ou inliers à l'aide de méthodes prédictives.

estimator.predict(X_train)

La valeur inlier est étiquetée 1 et la valeur aberrante est étiquetée -1.

2.7.1. Détection de nouveauté

Considérons un ensemble de données de $ n $ observations avec la même distribution que celle décrite par $ p $ features. Pensez maintenant à ajouter une autre observation à cet ensemble de données. Les nouvelles observations sont-elles si différentes des autres observations? (C'est-à-dire, vient-il de la même distribution?) Ou, au contraire, est-il si semblable aux autres qu'il est impossible de le distinguer de l'observation originale? C'est un problème résolu par les outils et méthodes de détection de nouveauté. En général, il essaie d'apprendre les limites approximatives et proches qui définissent la distribution d'observation initiale, tracée en incorporant l'espace de dimension $ p $. Ensuite, si d'autres observations se trouvent dans le sous-espace délimité par la frontière, elles sont considérées comme appartenant à la même population que la première observation. Sinon, s'ils se trouvent en dehors de la frontière, nous pouvons dire qu'ils sont anormaux avec une certaine confiance dans notre évaluation. La SVM à une classe a été introduite par Schölkopf et al. À cette fin, les machines vectorielles de support de l'objet svm.OneClassSVM (http://scikit-learn.org/0.18/modules/generated/sklearn.svm.OneClassSVM.html#sklearn.svm.OneClassSVM). http://qiita.com/nazoking@github/items/2b16be7f7eac940f2e6a) Il est implémenté dans le module. Pour définir la frontière, vous devez sélectionner les paramètres noyau et scalaire. Les noyaux RBF n'ont généralement pas de formule ou d'algorithme exact pour définir les paramètres de bande passante, mais ils sont choisis. Il s'agit de la valeur par défaut pour l'implémentation scicit-learn. Le paramètre $ \ nu $, également appelé marge SVM One-Class, correspond à la probabilité de trouver des observations nouvelles mais régulières en dehors de la frontière.

Les références:
Estimation de la prise en charge de la distribution haute dimension Schölkopf, Bernhard, et al. Neural Computing 13,7 (2001): 1443-1471.
Exemple:
svm.OneClassSVM La frontière apprise autour de certaines données par l'objet Pour la visualisation, [1 classe SVM avec noyau non linéaire (RBF)](http://scikit-learn.org/0.18/auto_examples/svm/plot_oneclass.html#sphx-glr-auto-examples-svm-plot Voir -oneclass-py).

2.7.2. Détection des valeurs aberrantes

La détection hors valeur est similaire à la détection de nouveauté en ce qu'elle sépare le noyau des observations normales de certains matériaux contaminés (appelés «valeurs aberrantes»). Cependant, dans le cas de la détection des valeurs aberrantes, nous n'avons pas de jeu de données propre qui représente une population d'observations régulières pouvant être utilisées pour entraîner n'importe quel outil.

2.7.2.1. Installer l'enveloppe ovale

Une manière courante d'effectuer la détection des valeurs aberrantes consiste à supposer que les données normales proviennent d'une distribution connue (par exemple, les données sont une distribution gaussienne). À partir de cette hypothèse, nous essayons généralement de définir la «forme» des données, et la valeur de l'écart peut être définie comme une valeur d'observation bien éloignée de la forme d'ajustement. scikit-learn fournit la co-distribution d'objets. L'enveloppe elliptique ajuste une estimation de covariance robuste aux données et ajuste l'ellipse au point de données central, en ignorant les points autres que le mode central. Par exemple, en supposant que les données initiales sont gaussiennes, la position initiale et la covariance sont estimées de manière robuste (c'est-à-dire non affectées par la valeur aberrante). La distance maharanobis obtenue à partir de cette estimation est utilisée pour dériver une mesure de l'exogène. Cette stratégie est illustrée ci-dessous.

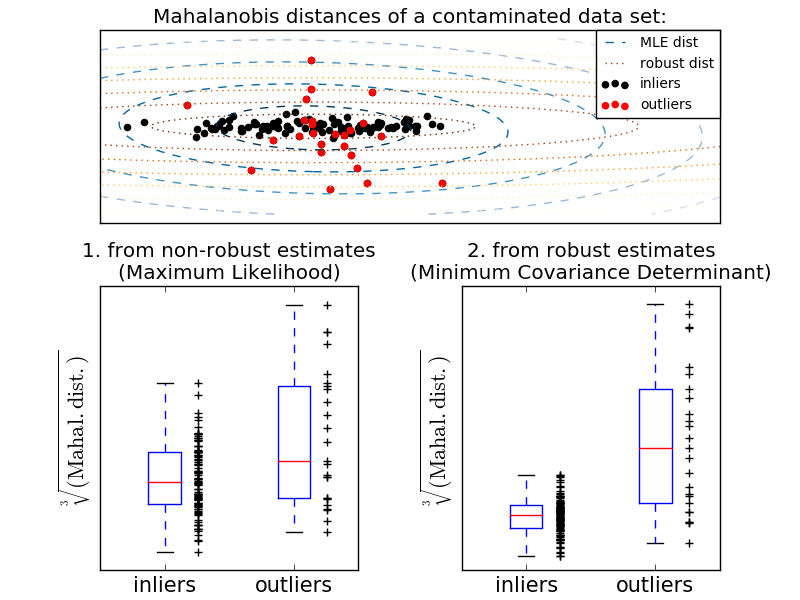
Exemple:
Standard (covariance.EmpiricalCovariance) pour évaluer le degré d'écart par rapport à l'observation ) Ou l'utilisation d'estimations robustes (covariance.MinCovDet) Pour expliquer la différence, voir [Relation entre l'estimation de la covariance robuste et la distance de Maharanobis](http://scikit-learn.org/0.18/auto_examples/covariance/plot_mahalanobis_distances.html#sphx-glr-auto-examples-covariance- Voir plot-mahalanobis-distances-py).
Les références:
[RD1999] Rousseeuw, P.J., Van Driessen, K. "Fast Algorithm for Minimum Covariance Matrix Estimator" Technometrics 41 (3), 212 (1999)

2.7.2.2. Forêt d'isolement

Un moyen efficace de détecter les valeurs aberrantes dans les ensembles de données de grande dimension consiste à utiliser une forêt aléatoire. ensemble.IsolationForest sélectionne au hasard les caractéristiques et maximise les caractéristiques sélectionnées. «Séparez» les observations en choisissant au hasard une répartition entre la valeur et le minimum. Les fractionnements récursifs peuvent être représentés dans une structure arborescente, de sorte que le nombre de fractionnements requis pour séparer les échantillons correspond à la longueur du chemin du nœud racine au nœud final. La longueur de ce chemin, moyennée sur une forêt d'arbres aussi aléatoire, est une mesure de normalité et de jugement. La division aléatoire produit un chemin significativement plus court pour les anomalies. Par conséquent, si une forêt d'arbres aléatoires produit de manière générique des chemins plus courts pour un échantillon particulier, ils sont susceptibles d'être anormaux. Cette stratégie est illustrée ci-dessous.

Exemple:
Pour des exemples d'utilisation d'IsolationForest, voir [Exemples IsolationForest](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_isolation_forest.html#sphx-glr-auto-examples-ensemble-plot-isolation-forest- Voir py).
Détection des valeurs aberrantes par plusieurs méthodes Prière de se référer à. ensemble.IsolationForest et [svm.OneClassSVM](http: // scikit-learn) .org / 0.18 / modules / generated / sklearn.svm.OneClassSVM.html # sklearn.svm.OneClassSVM) (optimisé pour la méthode de détection des valeurs aberrantes) et [covariance.MinCovDet](http: // scikit- Comparez la détection des valeurs aberrantes basée sur la covariance à l'aide de learn.org/0.18/modules/generated/sklearn.covariance.MinCovDet.html#sklearn.covariance.MinCovDet).
Les références:
[LTZ2008] Liu, Fei Tony, Ting, Kai Ming, Zhou, Zhi-Hua. Exploration de données "Separated Forest", 2008. ICDM '08. 8e conférence internationale de l'IEEE

2.7.2.3.1 Classe SVM vs enveloppe elliptique vs forêt d'isolement

Strictement parlant, un SVM à une classe est une nouvelle méthode de détection, pas une méthode de détection des valeurs aberrantes: l'ensemble d'apprentissage ne doit pas être contaminé car il est ajusté par les valeurs aberrantes. En bref, il est très difficile de détecter les valeurs aberrantes dans des dimensions plus élevées, ou de ne faire aucune hypothèse sur la distribution des données sous-jacentes, et les SVM à classe unique fournissent des résultats utiles dans ces situations. L'exemple suivant montre comment les performances co-distribuées se dégradent avec moins de données et moins.

svm.OneClassSVM fonctionne bien avec des données avec plusieurs modes et ensembles. IsolationForest fonctionne bien dans tous les cas.

Comparaison de l'approche SVM 1 classe et de l'enveloppe elliptique

Pour un mode inlier ovale bien centré, svm.OneClassSVM Vous ne pouvez pas bénéficier de la symétrie de rotation de la population inlier. De plus, il s'inscrit légèrement dans les valeurs aberrantes présentes dans l'ensemble d'apprentissage. Inversement, covariance.EllipticEnvelope basé sur l'ajustement de la covariance est une distribution inlier. Apprenez une ellipse qui ressemble beaucoup à. ensemble.IsolationForest fonctionne également.

L'enveloppe elliptique ne s'adapte pas bien aux inliers lorsque la distribution inlier devient bimodale. Cependant, covariance.EllipticEnvelope et [svm.OneClassSVM](http: // scikit) -Learn.org/0.18/modules/generated/sklearn.svm.OneClassSVM.html#sklearn.svm.OneClassSVM) ont tous deux des difficultés à détecter les deux modes, [svm.OneClassSVM](http: // scikit) Vous pouvez voir que -learn.org/0.18/modules/generated/sklearn.svm.OneClassSVM.html#sklearn.svm.OneClassSVM) a tendance à se substituer. Puisqu'il n'y a pas de modèle d'inliers, la zone dans laquelle certaines valeurs aberrantes sont regroupées est interprétée comme une valeur d'entrée.

Si la distribution initiale est forte et non gaussienne, svm.OneClassSVM est [ensemble.IsolationForest] ](Http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.IsolationForest.html#sklearn.ensemble.IsolationForest) peut restaurer une approximation raisonnable, mais covariance.EllipticEnvelope échoue complètement.

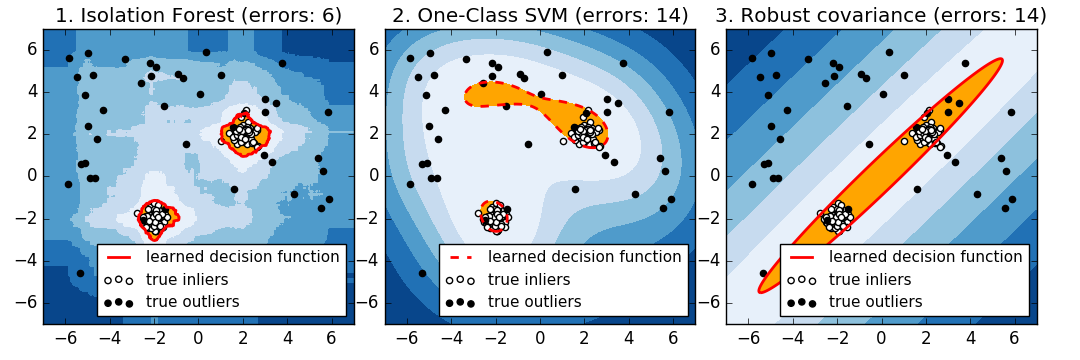
Exemple:
Pour des exemples d'utilisation d'IsolationForest, voir [Exemples IsolationForest](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_isolation_forest.html#sphx-glr-auto-examples-ensemble-plot-isolation-forest- Voir py).
Détection des valeurs aberrantes par plusieurs méthodes Prière de se référer à. ensemble.IsolationForest et [svm.OneClassSVM](http: // scikit-learn) .org / 0.18 / modules / generated / sklearn.svm.OneClassSVM.html # sklearn.svm.OneClassSVM) (optimisé pour la méthode de détection des valeurs aberrantes) et [covariance.MinCovDet](http: // scikit- Comparez la détection des valeurs aberrantes basée sur la covariance à l'aide de learn.org/0.18/modules/generated/sklearn.covariance.MinCovDet.html#sklearn.covariance.MinCovDet).

[scikit-learn 0.18 Guide de l'utilisateur 2. Apprendre sans enseignant](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA À partir de% E3% 81% 97% E5% AD% A6% E7% BF% 92)

[PYTHON] [Français] scikit-learn 0.18 Guide de l'utilisateur 2.7. Détection des nouveautés et des valeurs aberrantes