[PYTHON] [Français] scikit-learn 0.18 Guide de l'utilisateur 1.11. Méthode Ensemble
google traduit http://scikit-learn.org/0.18/modules/ensemble.html [scikit-learn 0.18 Guide de l'utilisateur 1. Apprentissage supervisé](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98 À partir de% E3% 81% 8D% E5% AD% A6% E7% BF% 92)
1.11. Méthode d'ensemble
L'objectif de ** Ensemble Learning ** est de combiner les prédictions de plusieurs estimateurs de base construits avec un algorithme d'apprentissage donné pour améliorer la polyvalence / robustesse pour un seul estimateur.
L'apprentissage d'ensemble est généralement divisé en deux familles.
-
** La méthode de moyennage ** est basée sur le principe que plusieurs estimateurs sont créés indépendamment et leurs valeurs prédites sont moyennées. En moyenne, les estimateurs combinés sont généralement meilleurs qu'un estimateur unique en raison de leur dispersion réduite.
-
Exemple: méthode d'ensachage, forêt d'arbres randomisée, ...
-
En revanche, la ** méthode d'amplification ** construit des estimateurs de base séquentiellement pour tenter de réduire le biais de l'estimateur de couplage. La motivation est de combiner plusieurs modèles faibles pour créer un ensemble puissant.
-
Exemple: AdaBoost, Gradient Tree Boost, ...
1.11.1. Méta-estimateur par ensachage
Dans l'algorithme d'ensemble, la méthode de bagging construit un estimateur de boîte noire sur un sous-ensemble aléatoire de l'ensemble d'apprentissage d'origine et forme une classe d'algorithmes qui agrège les prédictions individuelles pour former la prédiction finale. Ces méthodes introduisent la randomisation dans leurs procédures de construction et réduisent la dispersion des estimateurs de base (par exemple, les arbres de décision) en créant un ensemble. Dans de nombreux cas, la méthode de bagging constitue un moyen très simple d'améliorer sur un modèle unique sans avoir à adapter les algorithmes sous-jacents sous-jacents. Les méthodes d'ensachage sont généralement des modèles forts et complexes (par exemple, complètement), par opposition aux méthodes de stimulation les plus efficaces pour les modèles faibles (par exemple, arbres de décision peu profonds), car elles fournissent un moyen de réduire le surajustement. C'est le plus efficace dans l'arbre de décision déplié). Il existe de nombreux types de méthodes d'ensachage, mais la plupart d'entre elles diffèrent selon la façon dont vous dessinez un sous-ensemble aléatoire de votre ensemble d'entraînement.
- Cet algorithme est appelé Collage lorsqu'un sous-ensemble aléatoire de l'ensemble de données est dessiné comme un sous-ensemble aléatoire de l'échantillon. [B1999]
- Si vous souhaitez remplacer et prélever l'échantillon, cette méthode est connue sous le nom d'ensachage. [B1996]
- Lorsqu'un sous-ensemble aléatoire d'un ensemble de données est dessiné comme un sous-ensemble aléatoire d'entités, la méthode est connue sous le nom de sous-ensemble aléatoire. [H1998]
- Enfin, si l'estimateur de base est construit sur un sous-ensemble d'échantillons et de caractéristiques, cette méthode est connue sous le nom de patch aléatoire. [LG2012]
Dans scikit-learn, la méthode de bagging est BaggingClassifier Meta-estimator (et BaggingRegressor) ) avec des paramètres qui spécifient la stratégie pour dessiner un sous-ensemble aléatoire. Il prend un estimateur de base spécifié par l'utilisateur comme entrée. En particulier, «max_samples» et «max_features» contrôlent la taille du sous-ensemble (en termes d'échantillons et de fonctionnalités), tandis que «bootstrap» et «bootstrap_features» contrôlent s'il faut remplacer les échantillons et les fonctionnalités. Si vous utilisez un sous-ensemble des échantillons disponibles, vous pouvez estimer la précision de la généralisation dans l'échantillon hors sac en définissant ʻoob_score = True`. À titre d'exemple, l'extrait de code suivant montre comment instancier un ensemble d'ensachage de valeur de fonctionnalité basée sur KNeighborsClassifier construit avec un sous-ensemble aléatoire de 50% de l'échantillon et 50% de la fonctionnalité.
>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
... max_samples=0.5, max_features=0.5)
-
Exemple:
-
[Single Estimeter and Bagging: Bias Dispersion Decomposition](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_bias_variance.html#sphx-glr-auto-examples-ensemble-plot-bias-variance- py)
-
Les références
-
[B1999] L. Breiman, "Mettez un petit vote pour les grandes bases de données et la classification en ligne" Machine Learning, 36 (1), 85-103, 1999
-
[B1996] L. Breiman, "Prédicteurs d'ensachage", Machine Learning, 24 (2), 123-140, 1996 [H1998] T. Ho, «Méthode de sous-espace aléatoire pour la construction de forêts décisionnelles», Analyse de modèle et intelligence artificielle, 20 (8), 832-844, 1998.
-
[LG2012] G. Louppe et P. Geurts, «Ensemble de correctifs aléatoires», Apprentissage automatique et découverte des connaissances dans les bases de données, 346-361, 2012.
1.11.2. Forêt arborée aléatoire
sklearn.ensemble Le module a un [arbre de décision] randomisé appelé algorithme RandomForest et méthode Extra-Trees. Il contient deux algorithmes de calcul de moyenne basés sur (http://scikit-learn.org/0.18/modules/tree.html#tree). Les deux algorithmes sont des techniques de perturbation et de couplage spécialement conçues pour les arbres [B1998]. Cela signifie qu'en introduisant le caractère aléatoire dans la construction du classificateur, un ensemble diversifié de classificateurs est créé. Les prédictions d'ensemble sont données sous forme de prévisions moyennes pour les classificateurs individuels.
En tant qu'autre classificateur, le classificateur de forêt nécessite deux séquences. Tableau clairsemé ou dense X de taille [n_samples, n_features] pour contenir les échantillons d'apprentissage et le tableau Y de taille [n_samples] pour contenir les valeurs cibles (étiquettes de classe) Exemple d'entraînement:
>>> from sklearn.ensemble import RandomForestClassifier
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, Y)
Similaire à Arbre de décision, Tree Forest est un problème à sorties multiples. Il s'étend également à /modules/tree.html#tree-multioutput) (si Y est un tableau de taille [n_samples, n_outputs]).
1.11.2.1. Forêt aléatoire
Random Forest (RandomForestClassifier classe et [RandomForestRegressor](http: // scikit-learnRegressor](http: // scikit-learnRegressor)) Dans la classe .org / 0.18 / modules / generated / sklearn.ensemble.RandomForestRegressor.html # sklearn.ensemble.RandomForestRegressor)), chaque arbre de l'ensemble a été dessiné avec un remplacement de jeu de formation (c'est-à-dire, un échantillon bootstrap). Il est construit à partir de l'échantillon. De plus, si vous divisez un nœud lors de la construction d'un arbre, la division sélectionnée n'est plus la meilleure division de toutes les entités. Au lieu de cela, la division choisie est la meilleure division d'un sous-ensemble aléatoire de fonctionnalités. En raison de ce caractère aléatoire, le biais de la forêt augmente généralement légèrement (par rapport au biais d'un seul arbre non aléatoire), mais en raison de la moyenne, l'écart diminue également, compensant généralement le biais accru. Non seulement vous obtiendrez un meilleur modèle dans l'ensemble. Contrairement à l'article original [B2001], l'implémentation de scicit-learn combine des classificateurs en faisant la moyenne des prédictions probabilistes au lieu de faire voter chaque classificateur pour une seule classe.
1.11.2.2. Arbre très aléatoire
Arbre hautement aléatoire (classe ExtraTreesClassifier et [ExtraTreesRegressor](http :: //scikit-learn.org/0.18/modules/generated/sklearn.ensemble.ExtraTreesRegressor.html#sklearn.ensemble.ExtraTreesRegressor) Voir class)), ce qui pousse le caractère aléatoire un peu plus loin dans la façon dont les fractionnements sont calculés. Je vais. Comme pour les forêts aléatoires, un sous-ensemble aléatoire d'entités candidates est utilisé, mais au lieu de rechercher les seuils les plus importants, des seuils sont tirés au hasard pour chaque entité candidate et ceux-ci sont générés aléatoirement. La valeur la plus élevée du seuil est sélectionnée comme règle de fractionnement. Cela permet généralement de réduire la variance du modèle, même légèrement au prix d'une légère augmentation du biais.
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import make_blobs
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.tree import DecisionTreeClassifier
>>> X, y = make_blobs(n_samples=10000, n_features=10, centers=100,
... random_state=0)
>>> clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2,
... random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean()
0.97...
>>> clf = RandomForestClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean()
0.999...
>>> clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y)
>>> scores.mean() > 0.999
True
1.11.2.3. Paramètres
Les principaux paramètres à ajuster lors de l'utilisation de ces méthodes sont n_estimators et max_features. Le premier est le nombre d'arbres. Plus grand est mieux, mais le calcul prend plus de temps. De plus, gardez à l'esprit que traverser un nombre important d'arbres n'améliore pas significativement les résultats. Ce dernier est la taille d'un sous-ensemble aléatoire d'entités à prendre en compte lors de la division des nœuds. Plus la valeur est basse, plus la diminution de la dispersion est importante, mais plus l'augmentation du biais est importante. Une valeur par défaut empiriquement bonne est max_features = n_features pour les problèmes de régression et max_features = sqrt (n_features) pour les tâches de classification (n_features est le nombre de caractéristiques dans les données). Définir max_depth = None en combinaison avec min_samples_split = 1 (c'est-à-dire lorsque l'arborescence est complètement développée) donne souvent de bons résultats. Cependant, gardez à l'esprit que ces valeurs ne sont généralement pas optimales et peuvent entraîner des modèles qui consomment beaucoup de RAM. Les meilleures valeurs de paramètre doivent toujours être validées de manière croisée. Notez également que dans une forêt aléatoire, l'exemple de bootstrap est utilisé par défaut (bootstrap = True), et la stratégie par défaut de l'arborescence supplémentaire utilise l'ensemble de données ( bootstrap = False). Lors de l'utilisation de l'échantillonnage bootstrap, la précision de la généralisation peut être estimée avec des échantillons laissés de côté ou hors sac. Pour activer cela, définissez ʻoob_score = True`.
1.11.2.4. Parallélisation
Enfin, le module propose également une structure parallèle d'arbres et des calculs parallèles de prédictions avec le paramètre n_jobs. Si n_jobs = k, le calcul est divisé en k travaux et exécuté sur les cœurs k de la machine. Si n_jobs = -1, tous les cœurs disponibles sur la machine seront utilisés. En raison de la surcharge de communication inter-processus, l'accélération peut ne pas être linéaire (c'est-à-dire que l'utilisation d'un travail «k» n'est malheureusement pas «k» fois plus rapide). Des accélérations significatives peuvent être obtenues même lorsque la construction d'un grand nombre d'arbres ou même lorsque la construction d'un seul arbre nécessite un temps considérable (par exemple, un grand ensemble de données).
-
Exemple:
-
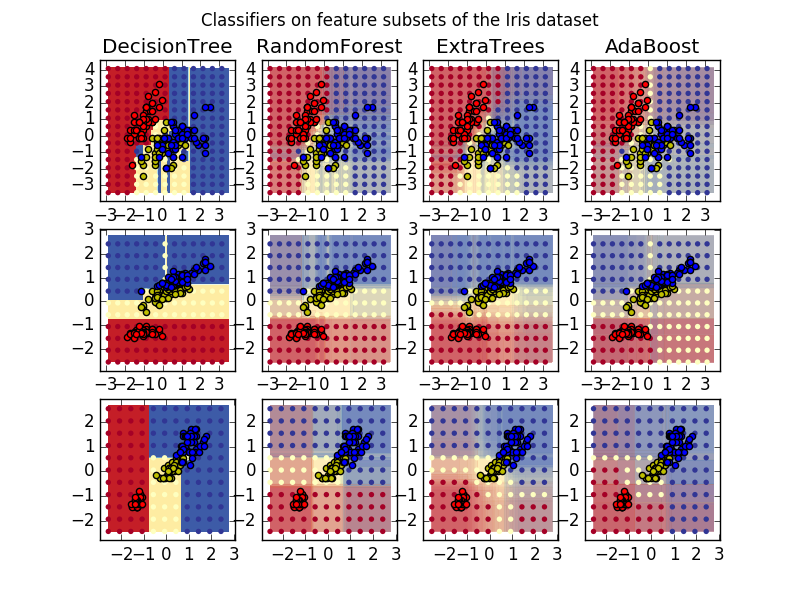
[Tracer le plan de décision de l'ensemble arborescent sur l'ensemble de données iris](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_forest_iris.html#sphx-glr-auto-examples-ensemble-plot-forest -iris-py)
-
[Importance des pixels dans les forêts d'arbres parallèles](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_forest_importances_faces.html#sphx-glr-auto-examples-ensemble-plot-forest-importances -faces-py)
-
Les références
-
[B2001] Breiman, "Random Forest", Machine Learning, 45 (1), 5-32, 2001.
- [B1998] Breiman、 "Arcing Classifiers"、Annals of Statistics 1998
-
[GEW2006] P. Geurts, D. Ernst. , Et L. Wehenkel, "Arbres super aléatoires", Machine Learning, 63 (1), 3-42, 2006.
1.11.2.5. Évaluation de l'importance de la quantité de caractéristiques
Le rang relatif (c'est-à-dire la profondeur) d'une entité utilisée comme nœud de décision dans l'arborescence peut être utilisé pour évaluer l'importance relative de cette caractéristique pour la prévisibilité de la variable cible. Les caractéristiques utilisées en haut de l'arbre contribuent à la détermination prédictive finale de la plus grande partie de l'échantillon d'entrée. Par conséquent, * la proportion attendue d'échantillons auxquels ils contribuent * peut être utilisée comme une estimation de l'importance relative * des * caractéristiques (variables explicatives). En * faisant la moyenne * de ces taux d'activité attendus sur plusieurs arbres randomisés, la * variance * de ces estimations peut être réduite * et utilisée pour la sélection des caractéristiques. .. L'exemple suivant est pour chaque pixel d'une tâche de reconnaissance faciale utilisant le modèle ExtraTreesClassifier. Affiche une représentation codée par couleur de la lecture relative.
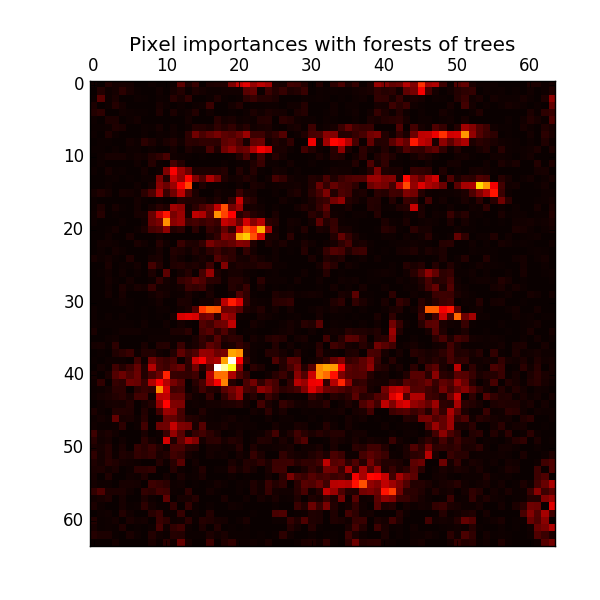
En pratique, ces estimations sont stockées dans le modèle ajusté sous la forme d'un attribut nommé «feature_importances_». C'est un tableau avec des valeurs positives pour la forme (n_features,) et une somme de 1,0. Plus la valeur est élevée, plus la contribution de la fonction de correspondance à la fonction prédictive est importante.
- Exemple:
- [Importance des pixels dans les forêts d'arbres parallèles](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_forest_importances_faces.html#sphx-glr-auto-examples-ensemble-plot-forest-importances -faces-py)
- Importation de fonctionnalités dans la forêt arborescente
1.11.2.6. Incorporation d'arbres entièrement aléatoire
RandomTreesEmbedding implémente une transformation de données non supervisée. À l'aide d'une forêt arborescente complètement aléatoire, RandomTreesEmbedding encode les données par l'index de la feuille où les points de données se terminent. Cet index est codé de manière K un-à-un, conduisant à un codage binaire clairsemé de plus grande dimension. Ce codage est calculé très efficacement et peut être utilisé comme base pour d'autres tâches d'apprentissage. La taille et la rareté du code peuvent être affectées en choisissant le nombre d'arbres et la profondeur maximale par arbre. Pour chaque arbre de l'ensemble, le codage contient une entrée. La taille de codage maximale est n_estimators * 2 ** max_depth, qui est le nombre maximum de feuilles dans la forêt.
La transformation effectue une estimation de densité non paramétrique implicite car les points de données adjacents sont susceptibles de se trouver dans la même feuille de l'arbre.
- Exemple:
- [Conversion de hachage utilisant un arbre complètement aléatoire](http://scikit-learn.org/0.18/auto_examples/ensemble/plot_random_forest_embedding.html#sphx-glr-auto-examples-ensemble-plot-random-forest-embedding -py)
- [Apprentissage multiple des nombres manuscrits: incorporation linéaire locale, Isomap ...](http://scikit-learn.org/0.18/auto_examples/manifold/plot_lle_digits.html#sphx-glr-auto-examples-manifold-plot -lle-digits-py) compare les techniques de réduction de dimension non linéaire pour les nombres manuscrits.
- Transformation des caractéristiques par ensemble d'arbres Compare une arborescence supervisée avec une transformation de fonctionnalité basée sur une arborescence non gérée.
Voir aussi: Manifold Learning (http://scikit-learn.org/0.18/modules/manifold.html#manifold) La technique permet également de dériver une représentation non linéaire de l'espace des fonctionnalités. Ces approches se concentrent également sur la réduction des dimensions.
1.11.3. AdaBoost
Le module sklearn.ensemble est un algorithme de boosting commun introduit par Freund et Schapire en 1995. Inclut AdaBoost [FS1995]. Le principe de base d'AdaBoost est d'adapter une séquence d'apprenants faibles (un modèle légèrement meilleur qu'une estimation aléatoire, comme un petit arbre de décision) à une version itérativement modifiée des données. Les prédictions de tous sont combinées par une majorité pondérée (ou somme) pour générer la prédiction finale. La modification des données à chaque itération d'amplification consiste à appliquer des poids $ w_1, w_2, ..., w_N $ à chacun des échantillons d'apprentissage. Au départ, tous ces poids sont fixés à $ w_i = 1 / N $, donc la première étape consiste simplement à former l'apprenant faible avec les données d'origine. À chaque itération, les poids de l'échantillon sont modifiés individuellement et l'algorithme d'apprentissage est réappliqué aux données repondérées. Dans une étape donnée, les exemples d'entraînement incorrectement prédits par le modèle boosté évoqué à l'étape précédente auront un poids accru, et ceux qui sont correctement prédits auront un poids diminué. Au fur et à mesure que les itérations progressent, les cas difficiles à prévoir sont de plus en plus affectés. Chaque apprenant faible suivant est obligé de se concentrer sur les exemples manqués par l'apprenant faible avant la séquence [HTF].
- AdaBoost peut être utilisé pour les problèmes de classification et de régression.
- Dans la classification multi-classes, [AdaBoostClassifier](http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.AdaBoostClassifier.html#sklearn] qui implémente AdaBoost-SAMME et AdaBoost-SAMME.R [ZZRH2009] .ensemble.AdaBoostClassifier).
- Pour la régression, utilisez AdaBoostRegressor qui implémente AdaBoost.R2 [D1997].
1.11.3.1. Utilisation
L'exemple suivant montre comment s'entraîner avec le classificateur AdaBoost en utilisant 100 apprenants faibles.
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import AdaBoostClassifier
>>> iris = load_iris()
>>> clf = AdaBoostClassifier(n_estimators=100)
>>> scores = cross_val_score(clf, iris.data, iris.target)
>>> scores.mean()
0.9...
Le nombre d'apprenants faibles est contrôlé par le paramètre n_estimators. Le paramètre learning_rate contrôle la contribution de l'apprenant faible à la combinaison finale. Par défaut, l'apprenant faible est Decision Stock. Vous pouvez spécifier un apprenant faible en utilisant le paramètre base_estimator. Les principaux paramètres à ajuster pour obtenir de bons résultats sont n_estimator et la complexité de l'estimation de base (par exemple, pour les arbres de profondeur, le nombre minimum d'échantillons requis en profondeur max_depth ou leaf min_samples_leaf). est.
-
Exemple:
-
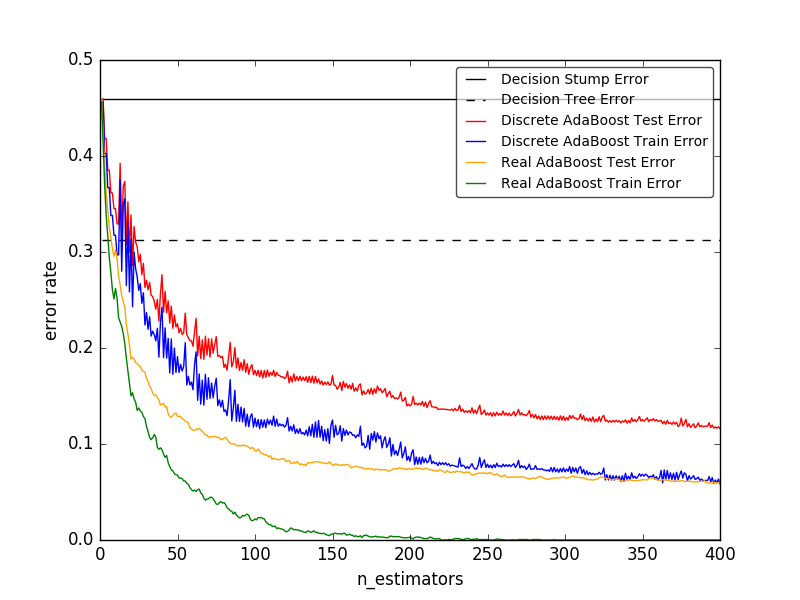
AdaBoost en nombre discret ou réel Utilise AdaBoost-SAMME et AdaBoost-SAMME.R pour comparer les erreurs de classification des souches de décision, des arbres de décision et des souches de décision boostées.
-
Arbres de décision Multiclass Ada Boosted Affiche les performances d'AdaBoost-SAMME et AdaBoost-SAMME.R pour les problèmes multiclasses.
-
2 classes d'AdaBoost est AdaBoost- Utilisez SAMME pour afficher la limite de décision et les valeurs de la fonction de décision pour un problème à deux classes séparables de manière non linéaire.
-
Decision Tree Regression by AdaBoost est AdaBoost Affiche la régression par l'algorithme .R2.
-
Les références
-
[FS1995] Y. Freund et R. Schapire, "Généralisation décisive de l'apprentissage en ligne et son application à la stimulation", 1997.
-
[ZZRH2009] J. Zhu, H. Zou, S. Rosset, T. Hastie. «Multiclass Ada Boost», 2009.
-
[D1997] Drucker. «Amélioration de la machine de retour utilisant la technologie de suralimentation», 1997.
-
[HTF] T. Hastie, R. Tibshirani et J. Friedman, «Elements of Statistical Learning Ed. 2», Springer, 2009.
1.11.4. Boost d'arbre de dégradé
Gradient Tree Boost (https://en.wikipedia.org/wiki/Gradient_boosting) ou Gradient Boost Regression Tree (GBRT) est une généralisation qui augmente à toute fonction de perte divisible. Le GBRT est une procédure prête à l'emploi précise et efficace qui peut être utilisée pour les problèmes de régression et de classification. Le modèle Gradient Tree Boosting est utilisé dans divers domaines, y compris les classements de recherche Web et l'écologie.
- Les avantages du GBRT sont:
- Traitement naturel des données mixtes (= caractéristiques hétérogènes)
- Puissance prédictive
- Robustesse aux valeurs aberrantes dans l'espace de sortie (grâce à une fonction de perte robuste)
- Les inconvénients du GBRT sont:
- En raison de la nature séquentielle du boosting, il peut difficilement être parallélisé.
Le module sklearn.ensemble fournit des méthodes de classification et de régression avec des arbres de régression boostés par gradient. Des offres.
1.11.4.1. Classification
GradientBoostingClassifier prend en charge la classification binaire et multiclasse. L'exemple suivant montre comment adapter un classificateur d'amplification de gradient en tant qu'apprenant faible avec 100 souches déterminées.
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.913...
Le nombre d'apprenants faibles (c'est-à-dire les arbres de régression) est contrôlé par le paramètre n_estimators. Pour chaque taille d'arbre (http://scikit-learn.org/0.18/modules/ensemble.html#gradient-boosting-tree-size), définissez la profondeur de l'arbre avec max_depth oumax_leaf_nodes Il peut être contrôlé en définissant le nombre de nœuds feuilles avec. learning_rate est un hyperparamètre de la plage (0.0, 1.0] qui contrôle le surajustement par shrink. est.
** Note: ** Une classification avec deux classes ou plus nécessite l'induction d'un arbre de régression n_classes à chaque itération, donc le nombre total d'arbres d'induction est égal à n_classes * n_estimators. Pour les ensembles de données avec de nombreuses classes, au lieu de GradientBoostingClassifier Nous vous recommandons vivement d'utiliser (http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.RandomForestClassifier.html#sklearn.ensemble.RandomForestClassifier).
1.11.4.2. Retour
GradientBoostingRegressor est une variété de pertes de régression qui peuvent être spécifiées par l'argument loss. Fonctions](http://scikit-learn.org/0.18/modules/ensemble.html#gradient-boosting-loss) est pris en charge. La fonction de perte par défaut pour la régression est le moindre carré (`` ls '').
>>> import numpy as np
>>> from sklearn.metrics import mean_squared_error
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
>>> X_train, X_test = X[:200], X[200:]
>>> y_train, y_test = y[:200], y[200:]
>>> est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
... max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
>>> mean_squared_error(y_test, est.predict(X_test))
5.00...
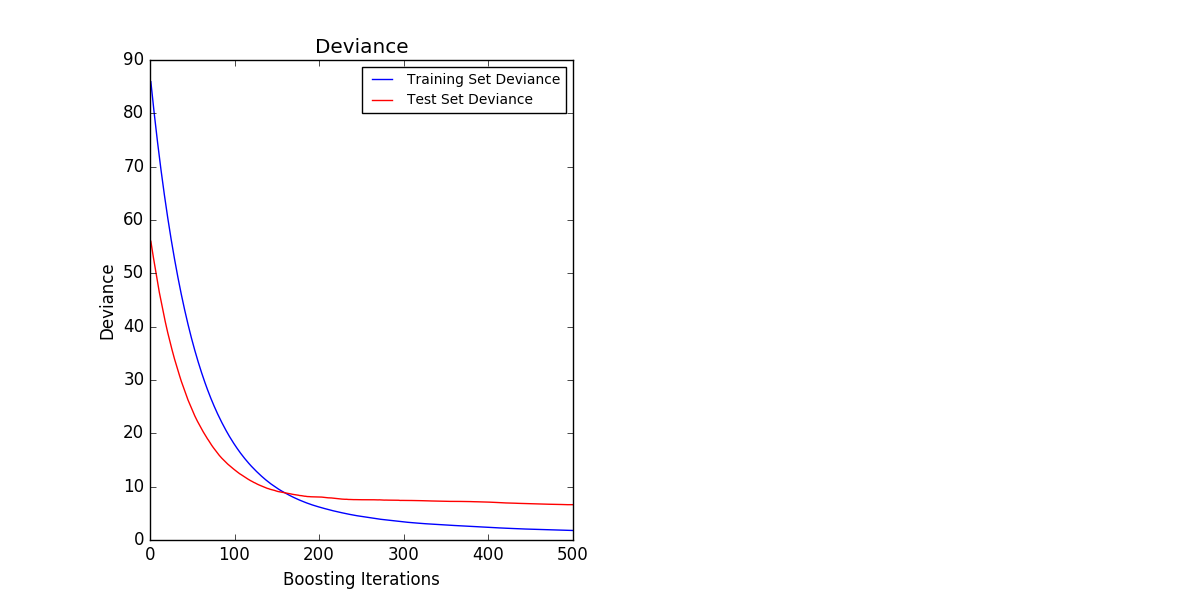
La figure ci-dessous montre l'ensemble de données sur les prix des maisons à Boston (sklearn.datasets.load_boston). ) Avec une perte quadratique minimale et un apprenant basé sur 500 appliqué [GradientBoostingRegressor](http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble. Le résultat de GradientBoostingRegressor) est affiché. Le tracé de gauche montre le train et l'erreur de test à chaque itération. L'erreur de train à chaque itération est stockée dans l'attribut train_score_ du modèle d'amplification de gradient. L'erreur de test à chaque itération renvoie un générateur qui génère une prédiction pour chaque étape [staged_predict](http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble. Elle peut être obtenue à l'aide de la méthode GradientBoostingRegressor.staged_predict). Vous pouvez utiliser un tel graphique pour déterminer le nombre optimal d'arbres (n_estimators) par arrêt anticipé. Le tracé de droite montre les importations d'entités qui peuvent être obtenues à l'aide de la propriété feature_importances_.
1.11.4.3. Apprentissage supplémentaire
GradientBoostingRegressor et [GradientBoostingClassifier.org](http://scikit-learn.org. /modules/generated/sklearn.ensemble.GradientBoostingClassifier.html#sklearn.ensemble.GradientBoostingClassifier) tous deux prennent en charge warm_start = True. Cela vous permet d'ajouter une formation à un modèle que vous avez déjà installé.
>>> _ = est.set_params(n_estimators=200, warm_start=True) # set warm_start and new nr of trees
>>> _ = est.fit(X_train, y_train) # fit additional 100 trees to est
>>> mean_squared_error(y_test, est.predict(X_test))
3.84...
1.11.4.4. Contrôle de la taille des arbres
La taille de l'instrument d'étude basé sur un arbre de régression définit le niveau d'interaction variable capturé par le modèle d'amplification de gradient. En général, les arbres avec une profondeur de «h» peuvent capturer des interactions de degré «h». Il existe deux façons de contrôler la taille des arbres de régression individuels.
Spécifier max_depth = h complète un arbre binaire avec une profondeur de h. Un tel arbre a (jusqu'à) un nœud feuille de «2 ** h» et un nœud divisé de «2 ** h-1».
Vous pouvez également utiliser le paramètre max_leaf_nodes pour contrôler la taille de l'arbre en spécifiant le nombre de nœuds feuilles. Dans ce cas, l'arbre s'agrandit en utilisant la meilleure première recherche, où le nœud avec les impuretés les plus améliorées est développé en premier. Un arbre avec max_leaf_nodes = k a k-1 nœuds séparés et peut modéliser les interactions jusqu'à max_leaf_nodes-1.
Nous avons trouvé que max_leaf_nodes = k donne des résultats comparables à max_depth = k-1, mais il est beaucoup plus rapide de s'entraîner, mais au prix d'erreurs d'entraînement légèrement plus élevées. Le paramètre max_leaf_nodes correspond à la variable J dans le chapitre Gradient Boost de [F2001] et est lié au paramètre ʻinteraction.depth du paquet gbm de R avec max_leaf_nodes == interaction.depth + 1`.
1.11.4.5. Prescription mathématique
GBRT considère un modèle additif de la forme:
F(x) = \sum_{m=1}^{M} \gamma_m h_m(x)
Où $ h_m (x) $ est une fonction de base, généralement appelée apprenant faible dans le contexte du boosting. Gradient Tree Boosting utilise un [arbre de décision] de taille fixe (http://scikit-learn.org/0.18/modules/tree.html#tree) comme apprenant faible. L'arbre de décision a plusieurs capacités qui peuvent être utiles pour améliorer votre capacité à travailler avec des données mixtes et à modéliser des fonctionnalités complexes. Comme d'autres algorithmes d'amplification, GBRT construit le modèle d'additionneur dans la phase directe.
F_m(x) = F_{m-1}(x) + \gamma_m h_m(x)
A chaque étape, l'arbre de décision $ h_m (x) $ est la fonction de perte $ L $ étant donné le modèle courant $ F_ {m-1} $ et son ajustement $ F_ {m-1} (x_i) $. Est sélectionné pour minimiser.
F_m(x) = F_{m-1}(x) + \arg\min_{h} \sum_{i=1}^{n} L(y_i,
F_{m-1}(x_i) - h(x))
Le modèle initial $ F_ {0} $ est spécifique au problème et choisit généralement la moyenne des valeurs cibles pour la régression au carré minimal.
Remarque: Le modèle initial peut également être spécifié avec l'argument init. L'objet transmis doit implémenter l'ajustement et la prédiction.
L'amplification du gradient tente de résoudre ce problème de minimisation numériquement par la descente la plus raide. La direction de descente la plus raide est le gradient négatif de la fonction de perte évaluée par le modèle courant $ F_ {m-1} $, qui peut être calculé pour toute fonction de perte divisible.
F_m(x) = F_{m-1}(x) + \gamma_m \sum_{i=1}^{n} \nabla_F L(y_i,
F_{m-1}(x_i))
Si vous spécifiez la longueur de ligne et sélectionnez la longueur de pas $ \ gamma_m $,
\gamma_m = \arg\min_{\gamma} \sum_{i=1}^{n} L(y_i, F_{m-1}(x_i)
- \gamma \frac{\partial L(y_i, F_{m-1}(x_i))}{\partial F_{m-1}(x_i)})
Les algorithmes de régression et de classification ne diffèrent que par la fonction de perte spécifique utilisée.
1.11.4.5.1. Fonction de perte
Les fonctions de perte suivantes sont prises en charge et peuvent être spécifiées à l'aide du paramètre loss.
- Revenir
- Carré minimum (`` ls ''): sélection naturelle de la régression grâce à d'excellentes caractéristiques de calcul. Le modèle initial est donné par la moyenne des valeurs cibles.
- Écart absolu minimum (`` lad ''): fonction Robustros de régression. Le modèle initial est donné par la valeur cible médiane.
- Huber (`` huber ''): Une autre fonction Robustros qui combine le moindre carré et l'écart absolu minimum. Utilisez ʻalpha` pour contrôler la sensibilité par rapport aux contours (voir [F2001] pour plus de détails).
- Quantile (`` quantile ''): fonction de perte de la régression par division. Utilisez «0 <alpha <1» pour spécifier le nombre de fractions. Vous pouvez utiliser cette fonction de perte pour créer un intervalle de prédiction (Intervalle de prédiction pour la régression d'amplification de gradient (http://scikit-learn.org/0.18/auto_examples/ensemble/plot_gradient_boosting_quantile.html#sphx-glr-) (voir auto-examples-ensemble-plot-gradient-boosting-quantile-py)).
- Classification
- Classification binaire (`` déviance ''): fonction de perte de probabilité log binaire négative pour la classification binomiale (fournit une estimation de probabilité). Le modèle initial est donné par le logarithme du rapport de cotes.
- Déviation polygonale (`` déviance ''): Logarithme polynomial négatif pour la classification multiclasse avec fonction de perte de probabilité de classe
n_classesmutuellement exclusive. Il fournit une estimation probabiliste. Le modèle initial est donné par la pré-probabilité de chaque classe. À chaque itération, vous devez créer un arbre de régression qui rend le GBRT plutôt inefficace pour les ensembles de données avec de nombreuses classes. - Perte exponentielle (`` exponentielle ''): Identique à AdaBoostClassifier Fonction de perte. Les exemples qui ne sont pas correctement étiquetés comme «déviance» ne sont pas très forts. Ne peut être utilisé que pour la classification binaire.
1.11.4.6. Normalisation
1.11.4.6.1. Rétrécissement
[F2001] a proposé une stratégie de régularisation simple qui met à l'échelle la contribution de chaque apprenant faible par un facteur. $ \ nu $:
F_m(x) = F_{m-1}(x) + \nu \gamma_m h_m(x)
Le paramètre $ \ nu $ est également appelé ** taux d'apprentissage ** car il met à l'échelle la longueur du pas de la procédure de descente de gradient. Il peut être défini à l'aide du paramètre learning_rate.
Le paramètre «learning_rate» interagit fortement avec le paramètre «n_estimators», qui correspond au nombre d'apprenants faibles. Plus la valeur de «learning_rate» est petite, plus les apprenants faibles sont nécessaires pour maintenir des erreurs d'entraînement constantes. Des preuves empiriques montrent que des valeurs plus petites pour learning_rate améliorent les erreurs de test. [HTF2009] recommande de régler le taux d'apprentissage sur une petite constante (par exemple, learning_rate <= 0.1) et de sélectionner n_estimators par arrêt anticipé. Pour plus d'informations sur l'interaction entre learning_rate et n_estimators, voir [R2007].
1.11.4.6.2. Sous-échantillonnage
[F1999] a proposé une augmentation de gradient probabiliste qui combine l'augmentation de gradient avec la moyenne bootstrap (bagging). A chaque itération, le classificateur de base est entraîné sur la fraction «sous-échantillon» des données d'apprentissage disponibles. Les sous-échantillons sont dessinés sans remplacement. Une valeur typique pour «sous-échantillon» est 0,5. La figure ci-dessous montre l'effet du retrait et du sous-échantillonnage sur l'ajustement du modèle. Vous pouvez clairement voir que la contraction ne se contracte pas. Le sous-échantillonnage avec retrait peut encore améliorer la précision du modèle. En revanche, le sous-échantillonnage sans retrait ne fonctionne pas très bien.
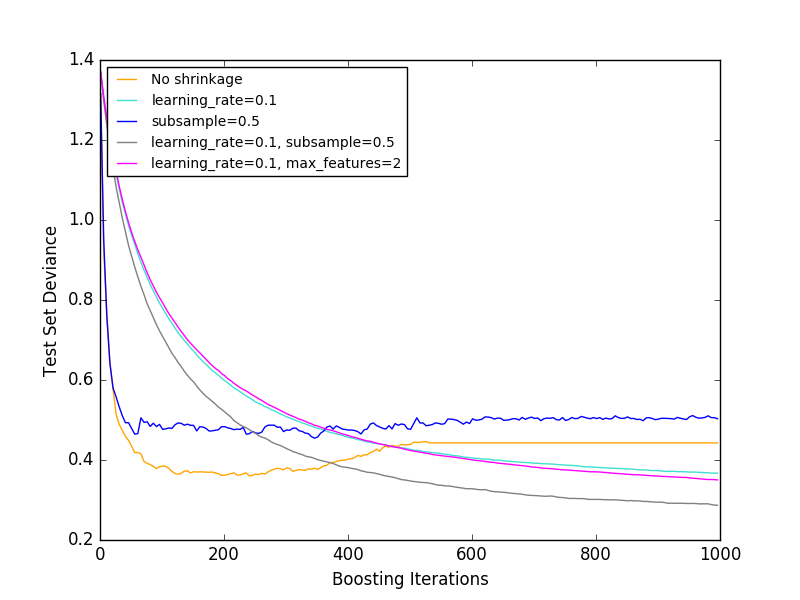
Une autre stratégie pour réduire la dispersion est similaire à la division aléatoire avec RandomForestClassifier. Il s'agit de sous-échantillonner la quantité de caractéristiques. Le nombre d'entités sous-échantillonnées peut être contrôlé par le paramètre max_features.
Remarque: la diminution de la valeur de max_features peut réduire considérablement le temps d'exécution.
L'amplification de gradient probabiliste permet de calculer des estimations hors sac des écarts de test en calculant l'amélioration des écarts pour les exemples non inclus dans l'échantillon bootstrap (c'est-à-dire les exemples hors sac). Les améliorations sont stockées dans l'attribut ʻoob_improvement_. ʻOob_improvement_ [i] conserve l'amélioration de la perte d'échantillon OOB lors de l'ajout de la i-ème étape à la prévision actuelle. Vous pouvez utiliser des estimations hors sac pour la sélection du modèle, comme la détermination du nombre optimal d'itérations. Les estimateurs OOB sont généralement très pessimistes, il est donc recommandé d'utiliser la validation mutuelle à la place et d'utiliser OOB uniquement si la validation mutuelle prend trop de temps.
- Exemple:
- Gradient Boosting Regularization
- Gradient Boost Out of Bag Estimate
- Erreur OOB de forêt aléatoire
1.11.4.7. Interprétation
Les arbres de décision individuels peuvent être facilement interprétés en visualisant simplement la structure arborescente. Cependant, le modèle de renforcement de gradient contient des centaines d'arbres de retour et ne peut pas être facilement interprété par une inspection visuelle des arbres individuels. Heureusement, de nombreuses techniques ont été proposées pour résumer et interpréter les modèles d'amplification de gradient.
1.11.4.7.1. Importance des fonctionnalités
Dans de nombreux cas, les fonctionnalités ne contribuent pas uniformément à prédire la réponse cible. Dans de nombreux cas, la plupart des fonctionnalités ne sont en fait pas pertinentes. Lors de l'interprétation d'un modèle, la première question est généralement de savoir quelles sont leurs principales caractéristiques et comment elles contribuent à prédire la réponse cible.
L'arbre de décision individuel effectue essentiellement la sélection des caractéristiques en sélectionnant les points de division appropriés. Ces informations peuvent être utilisées pour mesurer l'importance de chaque fonctionnalité. L'idée de base est que plus une fonction est utilisée fréquemment au niveau d'un point de division d'arbre, plus la fonction devient importante. Ce concept important peut être étendu à un ensemble d'arbres de décision en faisant simplement la moyenne de l'importance des fonctionnalités de chaque arbre (pour plus d'informations, Severity Rating (http: // scikit-). Voir learn.org/0.18/modules/ensemble.html#random-forest-feature-importance).
Le score d'importance des caractéristiques du modèle de renforcement du gradient d'ajustement est accessible à partir de la propriété feature_importances_.
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_
array([ 0.11, 0.1 , 0.11, ...
- Exemple:
- Gradient Boost Regression
1.11.4.7.2. Partiellement dépendant
Le diagramme de dépendance partielle (PDP) montre la dépendance entre la réponse cible et un ensemble de caractéristiques «cibles» qui délimitent les valeurs de toutes les autres caractéristiques (caractéristiques «complémentaires»). Intuitivement, nous pouvons interpréter la dépendance partielle comme une fonction de la caractéristique «cible» [2] et comme la réponse cible attendue [1]. En raison des limites de la perception humaine, la taille de l'ensemble de caractéristiques cible doit être petite (généralement une ou deux), de sorte que la caractéristique cible est généralement sélectionnée parmi les caractéristiques les plus importantes. La figure ci-dessous montre quatre parcelles unidirectionnelles et unidirectionnelles partiellement dépendantes de l'ensemble de données résidentielles de la Californie.
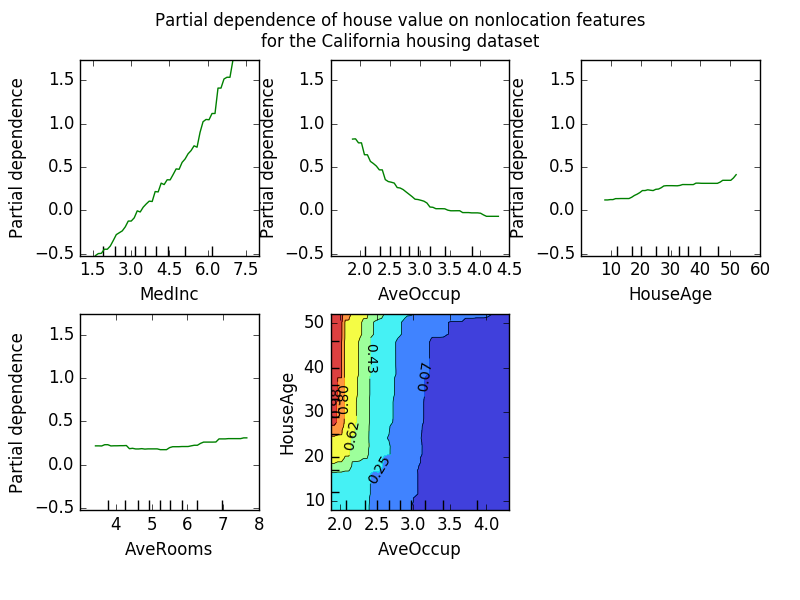
Le PDP unidirectionnel enseigne l'interaction entre la réponse cible et les caractéristiques cibles (par exemple linéaire, non linéaire). Le graphique en haut à gauche de la figure ci-dessus montre l'effet du revenu moyen dans un quartier sur les prix médians des logements. Nous pouvons clairement voir la relation linéaire entre eux. Un PDP avec deux fonctionnalités cibles - montre une interaction entre les deux fonctionnalités. Par exemple, le PDP à deux variables de la figure ci-dessus montre comment le prix médian du logement dépend de la valeur conjointe de l'âge du ménage et de la moyenne. Nombre d'occupants par ménage. Vous pouvez clairement voir l'interaction entre les deux fonctionnalités. Pour deux personnes ou plus, le prix de la maison est presque indépendant de l'âge de la maison, tandis que pour moins de deux personnes, il dépend fortement de l'âge. Le module partial_dependence est une fonction pratique plot_partial_dependence qui crée des tracés de dépendance partiels unidirectionnels et bidirectionnels. sklearn.ensemble.partial_dependence.plot_partial_dependence). L'exemple suivant montre comment créer une grille de graphiques partiellement dépendants. Deux PDP unidirectionnels avec des caractéristiques «0» et «1» et des PDP bidirectionnels entre les deux caractéristiques.
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.ensemble.partial_dependence import plot_partial_dependence
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> fig, axs = plot_partial_dependence(clf, X, features)
Pour les modèles multiclasses, vous devez utiliser l'argument label pour définir l'étiquette de classe qui crée le PDP.
>>>
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
... max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> fig, axs = plot_partial_dependence(mc_clf, X, features, label=0)
Si vous voulez la valeur brute d'une fonction partiellement dépendante au lieu d'un tracé, alors [partial_dependence](http://scikit-learn.org/0.18/modules/generated/sklearn.ensemble.partial_dependence.partial_dependence.html#sklearn.ensemble. Vous pouvez utiliser la fonction partial_dependence.partial_dependence):
>>>
>>> from sklearn.ensemble.partial_dependence import partial_dependence
>>> pdp, axes = partial_dependence(clf, [0], X=X)
>>> pdp
array([[ 2.46643157, 2.46643157, ...
>>> axes
[array([-1.62497054, -1.59201391, ...
La fonction nécessite soit l'argument «grid», qui spécifie la valeur de la fonction cible pour laquelle la fonction de dépendance partielle doit être évaluée, soit l'argument «X», qui est un mode simple pour créer automatiquement une grille à partir des données d'entraînement. Faire. Si «X» est spécifié, la valeur de l'axe renvoyée par la fonction sera l'axe de chaque quantité d'entités cible. Pour chaque valeur de la caractéristique «cible» dans la «grille», la fonction partiellement dépendante doit éloigner la prédiction de l'arbre à travers toutes les valeurs possibles de la caractéristique «complémentaire». Dans l'arbre de décision, cette fonctionnalité peut être évaluée efficacement sans référence aux données d'apprentissage. Pour chaque point de la grille, un parcours d'arborescence pondéré est effectué: si le nœud fractionné contient des entités "cibles", il se branche vers la gauche ou la droite correspondante. Sinon, suivez les deux branches. Chaque branche est pondérée avec le pourcentage d'échantillons d'apprentissage dans cette branche. Enfin, la dépendance partielle est donnée par la moyenne pondérée de tous les récifs visités. Pour les ensembles d'arbres, les résultats pour les arbres individuels sont recalibrés.
-
Note de bas de page
-
[1] Dans la classification perte = 'écart', la réponse cible est logit (p).
-
[2] Plus précisément, l'attente de la réponse cible après avoir considéré le modèle initial. Le graphe de dépendances partielles n'inclut pas le modèle init.
-
Exemple:
-
Les références
-
[F2001](1, 2, 3) J. Friedman, "Approximation de fonction gourmande: Machine à booster de gradient", Rapport statistique annuel, vol. Volume 29, numéro 5, 2001.
-
[F1999] Friedman, "Probabilistic Gradient Boost", 1999
-
[HTF2009] Hastie, R. Tibshirani et J. Friedman, «Elements of Statistical Learning Ed. 2», Springer, 2009.
-
[R2007] Ridgeway, "Generalized Boosted Models: gbm Package Guide", 2007
1.11.5. VotingClassifier
L'idée derrière l'implémentation du classificateur de vote est de combiner des classificateurs d'apprentissage automatique conceptuellement différents et de prédire les étiquettes de classe à l'aide du vote majoritaire ou de la probabilité prédictive moyenne (vote doux). Ces classificateurs peuvent être utiles dans un ensemble de modèles qui fonctionnent tout aussi bien pour équilibrer les faiblesses individuelles.
1.11.5.1. Étiquettes pour la majorité des classes (majorité / sélection rigoureuse)
Lors d'un vote majoritaire, l'étiquette de classe prédictive pour un échantillon particulier est l'étiquette de classe qui représente la majorité (mode) de l'étiquette de classe prédite par les classificateurs individuels.
Par exemple, la prédiction d'un échantillon donné
- Classificateur 1 → Classe 1
- Classificateur 2 → Classe 1
- Classificateur 3 → Classe 2
VotingClassifier (oting = 'hard') classe les échantillons comme "Classe 1" en fonction d'un grand nombre d'étiquettes de classe.
S'ils sont égaux, VotingClassifier sélectionne la classe en fonction de l'ordre de tri croissant. Par exemple, dans le scénario suivant
- Classificateur 1 → Classe 2
- Classificateur 2 → Classe 1
L'étiquette de classe 1 est attribuée à l'échantillon.
1.11.5.1.1. Utilisation
L'exemple suivant montre comment adapter un classificateur de règle majoritaire.
>>> from sklearn import datasets
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import VotingClassifier
>>> iris = datasets.load_iris()
>>> X, y = iris.data[:, 1:3], iris.target
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='hard')
>>> for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
... scores = cross_val_score(clf, X, y, cv=5, scoring='accuracy')
... print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
Accuracy: 0.90 (+/- 0.05) [Logistic Regression]
Accuracy: 0.93 (+/- 0.05) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [naive Bayes]
Accuracy: 0.95 (+/- 0.05) [Ensemble]
1.11.5.2. Probabilité moyenne pondérée (vote modéré)
Contrairement à la majorité des votes (votes durs), les votes doux renvoient l'étiquette de classe comme l'argmax total des probabilités prédites.
Des poids spécifiques peuvent être attribués à chaque classificateur via le paramètre «poids». Compte tenu des poids, les probabilités de classe prédites pour chaque classificateur sont collectées, les poids du classificateur sont multipliés et moyennés. L'étiquette de classe finale est dérivée de l'étiquette de classe avec la probabilité moyenne la plus élevée.
Pour expliquer cela avec un exemple simple, supposons qu'il existe trois classificateurs, w1 = 1, w2 = 1 et w3 = 1, et trois classes de problèmes de classification qui attribuent des poids égaux à tous les classificateurs. Je vais.
La probabilité moyenne pondérée de l'échantillon est calculée comme suit:
| Trieur | Classe 1 | Classe 2 | Classe 3 |
|---|---|---|---|
| Classificateur 1 | w1 * 0.2 | w1 * 0.5 | w1 * 0.3 |
| Classificateur 2 | w2 * 0.6 | w2 * 0.3 | w2 * 0.1 |
| Classificateur 3 | w3 * 0.3 | w3 * 0.4 | w3 * 0.3 |
| moyenne pondérée | 0.37 | 0.4 | 0.23 |
Ici, l'étiquette de classe prédictive est 2 car elle a la probabilité moyenne la plus élevée. L'exemple suivant montre comment la région de décision change lorsque le logiciel VotingClassifier est utilisé sur la base d'une machine vectorielle de support linéaire, d'un arbre de décision et d'un classificateur près de K.
>>> from sklearn import datasets
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> from sklearn.svm import SVC
>>> from itertools import product
>>> from sklearn.ensemble import VotingClassifier
>>> # Loading some example data
>>> iris = datasets.load_iris()
>>> X = iris.data[:, [0,2]]
>>> y = iris.target
>>> # Training classifiers
>>> clf1 = DecisionTreeClassifier(max_depth=4)
>>> clf2 = KNeighborsClassifier(n_neighbors=7)
>>> clf3 = SVC(kernel='rbf', probability=True)
>>> eclf = VotingClassifier(estimators=[('dt', clf1), ('knn', clf2), ('svc', clf3)], voting='soft', weights=[2,1,2])
>>> clf1 = clf1.fit(X,y)
>>> clf2 = clf2.fit(X,y)
>>> clf3 = clf3.fit(X,y)
>>> eclf = eclf.fit(X,y)
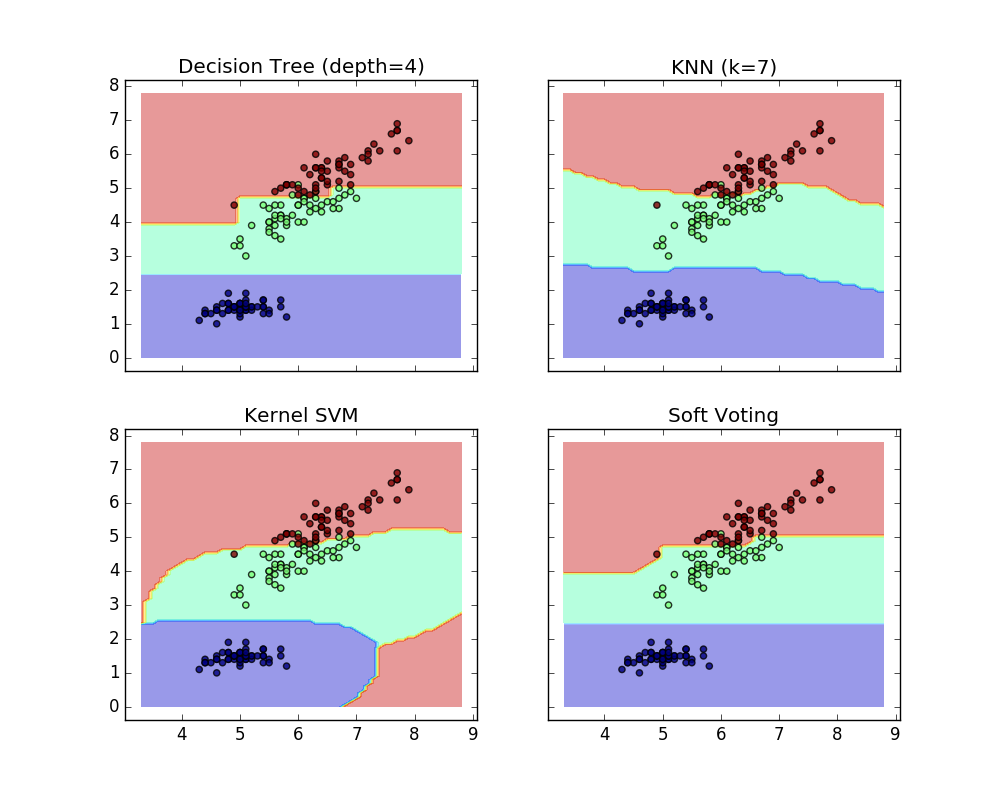
1.11.5.3. Utilisation du classificateur de vote avec la recherche de grille
VotingClassifier peut également être utilisé avec GridSearch pour ajuster les hyperparamètres des estimateurs individuels.
>>> from sklearn.model_selection import GridSearchCV
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft')
>>> params = {'lr__C': [1.0, 100.0], 'rf__n_estimators': [20, 200],}
>>> grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
>>> grid = grid.fit(iris.data, iris.target)
1.11.5.3.1 Utilisation
Pour prédire les étiquettes de classe en fonction des probabilités de classe prédites (les estimateurs scikit-learn de VotingClassifier doivent prendre en charge la méthode predict_proba)
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft')
Vous pouvez éventuellement pondérer des classificateurs individuels.
>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='soft', weights=[2,5,1])
[scikit-learn 0.18 Guide de l'utilisateur 1. Apprentissage supervisé](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98 À partir de% E3% 81% 8D% E5% AD% A6% E7% BF% 92)
© 2010 --2016, développeurs scikit-learn (licence BSD).
Recommended Posts