[PYTHON] [Français] scikit-learn 0.18 Guide de l'utilisateur 2.5. Décomposer les signaux en composants (problème de décomposition de la matrice)

google traduit http://scikit-learn.org/0.18/modules/decomposition.html

[Contenu du guide de l'utilisateur](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA%E3%81%97%E5 % AD% A6% E7% BF% 92)

2.5. Décomposer le signal dans le composant (problème de décomposition matricielle)

2.5.1. Analyse en composantes principales (ACP)

2.5.1.1. ACP précise et interprétation probabiliste

La PCA est utilisée pour décomposer des ensembles de données multivariées en un ensemble de composantes orthogonales consécutives qui expliquent la quantité maximale de dispersion. Dans scikit-learn, PCA utilise la méthode fit pour n composants. Il est implémenté en tant qu'objet transformateur qui forme et projette sur ces composants avec de nouvelles données. Le paramètre facultatif whiten = True vous permet de projeter des données dans un espace singulier tout en mettant à l'échelle chaque composant à une distribution d'unité. Ceci est souvent utile si l'aval du modèle présuppose fortement le signal isotrope. C'est le cas, par exemple, d'une machine à vecteur de support utilisant le noyau RBF et l'algorithme de clustering K-Means. Voici un exemple de jeu de données iris. Il se compose de quatre éléments, projetés sur deux dimensions, et la majeure partie de la dispersion est décrite.

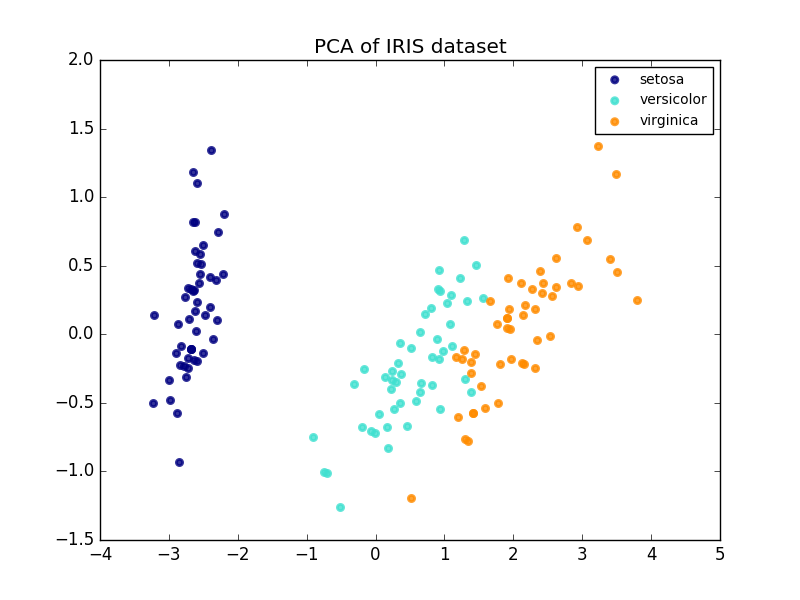
L'objet PCA fournit également une interprétation probabiliste de l'ACP, qui peut donner un potentiel de données basé sur la quantité de variance qu'il décrit. De cette façon, nous implémentons une méthode de score qui peut être utilisée pour l'authentification mutuelle.

• Exemple:
• [Comparaison de la projection 2D LDA et PCA du jeu de données iris](http://scikit-learn.org/0.18/auto_examples/decomposition/plot_pca_vs_lda.html#sphx-glr-auto-examples-decomposition-plot-pca-vs -lda-py)
• [Sélection du modèle par PCA probabiliste et analyse factorielle (FA)](http://scikit-learn.org/0.18/auto_examples/decomposition/plot_pca_vs_fa_model_selection.html#sphx-glr-auto-examples-decomposition-plot-pca- vs-fa-model-selection-py)

2.5.1.2. ACP incrémentale

PCA Les objets sont très utiles, mais présentent certaines limitations pour les grands ensembles de données. il y a. PCA ne prend en charge que le traitement par lots, toutes les données traitées doivent donc tenir dans la mémoire principale. IncrementalPCA L'objet utilise une forme de traitement différente et est presque le même que le résultat de l'ACP. Il permet des calculs partiels qui correspondent exactement et traite les données de manière mini-batch. IncrementalPCA vous permet de mettre en œuvre une analyse des composants principaux hors cœur de l'une des manières suivantes:

• Utilisez la méthode partial_fit pour les morceaux de données récupérés séquentiellement à partir d'un disque dur local ou d'une base de données réseau.
• Appelez la méthode fit sur un fichier mappé en mémoire en utilisant numpy.memmap.

IncrementalPCA ne stocke que les estimations de la distribution des composants et du bruit et met à jour ʻexplain_variance_ratio_` par étapes. Pour cette raison, l'utilisation de la mémoire dépend du nombre d'échantillons par lot, et non du nombre d'échantillons traités par l'ensemble de données.

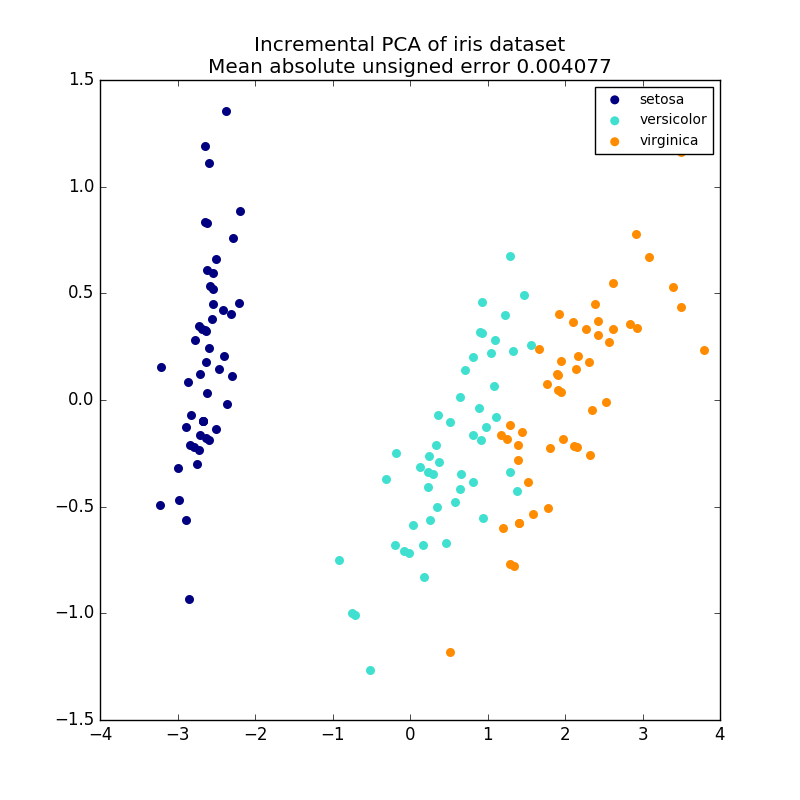
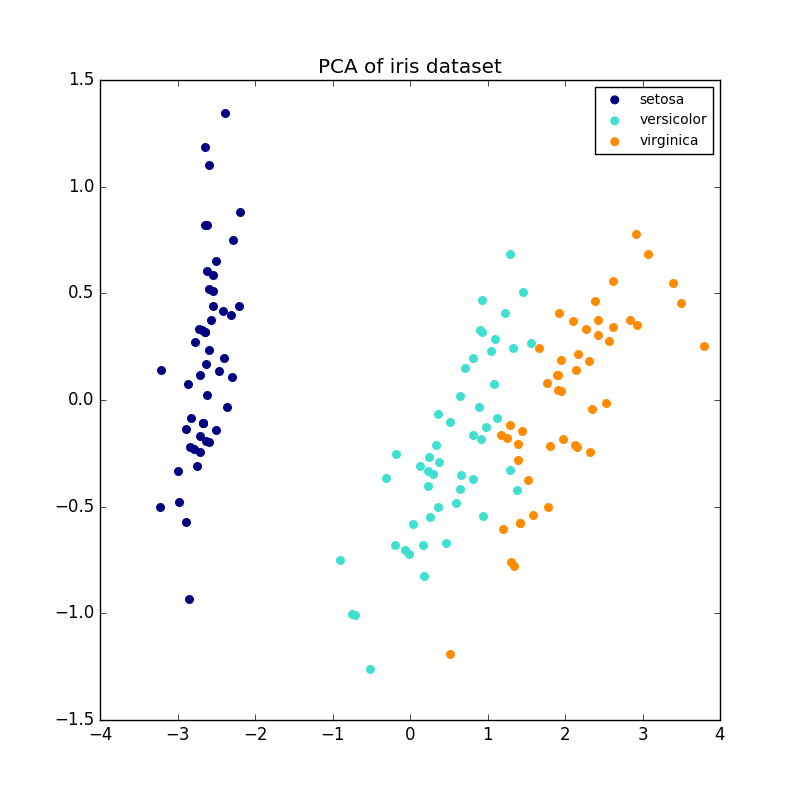
• Exemple:
• PCA incrémental

2.5.1.3. PCA avec SVD aléatoire

Il est souvent intéressant de projeter des données dans un espace dimensionnel inférieur qui préserve la plupart des variances en supprimant les vecteurs de singularité des composants associés à des valeurs plus singulières. Par exemple, lorsqu'il s'agit d'une image de niveau de gris de 64 x 64 pixels pour la reconnaissance faciale, la dimension des données est de 4 096 et l'apprentissage d'une machine vectorielle de support RBF pour une si large gamme de données est lent. De plus, toutes les images du visage humain sont quelque peu similaires, nous pouvons donc voir que l'égalité des données est bien inférieure à 4096. L'échantillon est sur une variété de dimensions beaucoup plus faibles (par exemple, environ 200). L'algorithme PCA peut être utilisé pour transformer linéairement des données, tout en réduisant les dimensions et en préservant la plupart des variances décrites. La classe PCA utilisée avec le paramètre optionnel svd_solver = 'randomized' est très utile dans de tels cas. Il est beaucoup plus efficace de limiter le calcul à des estimations approximatives du vecteur singulier, car il supprime la plupart des vecteurs singuliers. Veuillez effectuer la conversion. Par exemple, voici 16 exemples de portraits (centrés autour de 0,0) du jeu de données Olivetti. Sur la droite se trouvent les 16 premiers vecteurs singuliers reconstruits sous forme de portraits. Le temps de calcul est inférieur à 1 seconde car seuls les 16 premiers vecteurs singuliers de l'ensemble de données de $ n_ {samples} = 400 $ et $ n_ {features} = 64 \ times 64 = 4096 $ sont nécessaires.

Remarque: Vous devez également utiliser le paramètre facultatif svd_solver = 'randomized' pour donner à l'ACP la taille de l'espace de faible dimension n_components comme paramètre d'entrée obligatoire.

En se concentrant sur $ n_ {max} = max (n_ {échantillons}, n_ {fonctionnalités}) $ et $ n_ {min} = min (n_ {échantillons}, n_ {fonctionnalités}) $, la complexité temporelle de l'ACP aléatoire Soit $ O (n_ {max} ^ 2 \ cdot n_ {min}) $ au lieu de $ O (n_ {max} ^ 2 \ cdot n_ {composants}) $ dans la méthode exacte implémentée dans PCA. L'empreinte mémoire aléatoire PCA est de $ n_ {max} de la manière exacte Il est proportionnel à $ 2 \ cdot n_ {max} \ cdot n_ {composants} $ au lieu de \ cdot n_ {min} $. Remarque: l'implémentation de ʻinverse_transform dans PCA avec svd_solver = 'randomized'n'est pas l'inverse exact detransform même avec whiten = False` (par défaut).

• Exemple:
• Exemple de reconnaissance utilisant un visage unique et SVM
• Face Dataset Decomposition
• Les références:
• Trouver des structures aléatoires: algorithmes probabilistes pour construire une décomposition matricielle approximative Halko, et al. , 2009

2.5.1.4. PCA du noyau

KernelPCA est une extension de PCA qui réalise une réduction de dimension non linéaire en utilisant le noyau. (Voir Pair Metrics, Affinity and Kernel (http://scikit-learn.org/0.18/modules/metrics.html#metrics)). Il a de nombreuses applications telles que la réduction du bruit, la compression et la prédiction structurée (estimation des dépendances du noyau). KernelPCA prend en charge à la fois transform et ʻinverse_transform`.

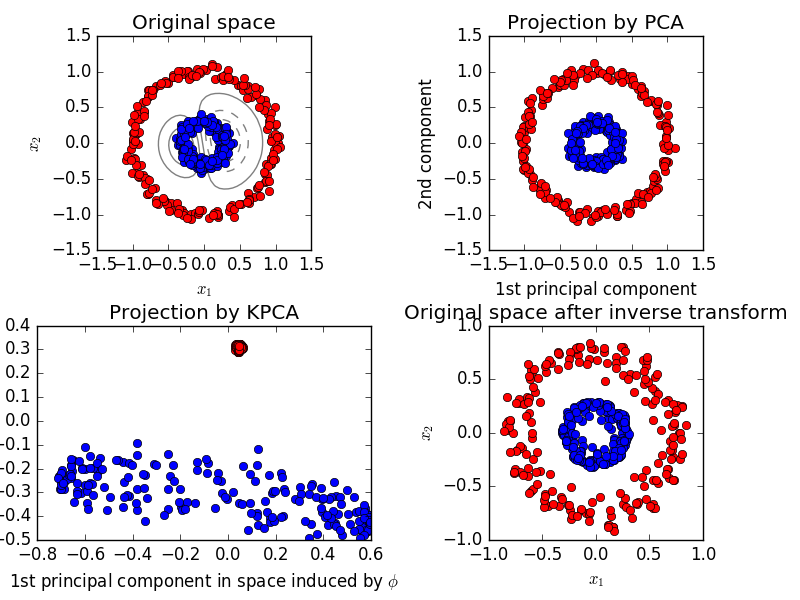
• Exemple:
• Kernel PCA

2.5.1.5. Analyse fragmentaire des principaux composants (SparsePCA et MiniBatchSparsePCA)

SparsePCA extrait l'ensemble des composants clairsemés qui reconstruisent le mieux les données. C'est une variante du PCA dans le but de MiniBatchSparsePCA (MiniBatchSparsePCA) est une variante de SparsePCA et est plus rapide. Cependant, la précision est inférieure. L'augmentation de la vitesse est obtenue en répétant de petits morceaux de l'ensemble de fonctionnalités pour un nombre spécifié d'itérations. L'analyse en composantes principales (ACP) présente l'inconvénient que les composantes extraites par cette méthode ont une représentation exclusivement dense, c'est-à-dire un coefficient non nul lorsqu'elles sont représentées comme une combinaison linéaire des variables d'origine. Cela peut être difficile à interpréter. Dans de nombreux cas, le composant sous-jacent réel peut être plus naturellement imaginé comme un vecteur clairsemé. Par exemple, dans la reconnaissance faciale, les composants peuvent naturellement correspondre à des parties du visage. La composante principale clairsemée souligne clairement laquelle des caractéristiques originales contribue aux différences entre les échantillons, ce qui donne une représentation plus concise et interprétable. L'exemple suivant montre 16 composants extraits à l'aide de SparsePCA à partir du jeu de données de face Olivetti. Vous pouvez voir comment le terme de normalisation dérive de nombreux zéros. De plus, la structure naturelle des données rend les coefficients non nuls verticalement adjacents. Le modèle ne force pas cela mathématiquement. Chaque composant est un vecteur $ h \ in \ mathbf {R} ^ {4096} $, et il n'y a pas de concept de contiguïté verticale sauf lors de visualisations conviviales telles que des images de 64 x 64 pixels. Le fait que les composants présentés ci-dessous apparaissent localement est un effet de la structure unique des données, et de tels modèles locaux minimisent les erreurs de reconstruction. Il existe des normes qui induisent une parcimonie compte tenu de la contiguïté et de divers types de structures. Voir [Jen09] pour une revue de ces méthodes. Pour plus d'informations sur l'utilisation de Sparse PCA, consultez la section exemple ci-dessous.

Notez qu'il existe de nombreuses expressions différentes dans le problème SparsePCA. Ce qui est implémenté ici est basé sur [Mrl09]. Le problème d'optimisation résolu est le problème PCA (apprentissage du dictionnaire), qui a une pénalité $ \ ell_1 $ sur le composant.

(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2}
             ||X-UV||_2^2+\alpha||V||_1 \\
             \text{subject to\,} & ||U_k||_2 = 1 \text{ for all }
             0 \leq k < n_{components}

La norme $ \ ell_1 $, qui induit une parcimonie, protège également le composant d'apprentissage du bruit lorsque peu d'échantillons d'apprentissage sont disponibles. Le degré de pénalité (et donc la parcimonie) peut être ajusté via l'hyperparamètre «alpha». Les petites valeurs entraînent une factorisation vaguement régularisée et les grandes valeurs réduisent de nombreux coefficients à zéro.

** Remarque: ** Dans l'algorithme en ligne, la classe MiniBatchSparsePCA est `` partial_fit Il n'implémente pas parce que l'algorithme est en ligne le long de la direction de l'entité, pas de la direction de l'échantillon.

• Exemple:
• Ensemble de données de visage de décomposition
• Les références:
• \ [Mrl09] Apprentissage de dictionnaires en ligne pour le codage clairsemé J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009
• \ [Jen09] Analyse en composantes principales structurées éparses R. Jenatton, G. Obozinski , F. Bach, 2009

2.5.2. Décomposition des singularités de troncature et analyse sémantique latente

TruncatedSVD a $ k $ dont $ k $ est un paramètre spécifié par l'utilisateur. Implémente une variante de la décomposition de singularité (SVD) qui ne calcule que la singularité maximale de. Lorsque le SVD tronqué est appliqué à une matrice terme-document (renvoyée par CountVectorizer ou TfidfVectorizer), cette transformation est [analyse sémantique latente (LSA)](http: //nlp.stanford). Connu sous le nom de .edu / IR-book / pdf / 18lsi.pdf). Il s'agit de transformer la matrice en un espace «sémantique» de dimension inférieure. En particulier, les LSA sont connus pour combattre les effets des synonymes et des polynomies (les deux signifiant au sens large plusieurs significations). Cela indique que le terme matrice de document est trop clairsemé et a une faible similitude par des moyens tels que la similitude cosinus.

** Remarque: ** LSA, également connu sous le nom d'indexation latente, LSI, est strictement utilisé pour les index persistants à des fins de recherche d'informations.

Mathématiquement, le SVD tronqué appliqué à l'échantillon d'apprentissage $ X $ produit une approximation de rang bas $ X $.

X \approx X_k = U_k \Sigma_k V_k^\top

Après cette opération, $ U_k \ Sigma_k ^ \ top $ est un ensemble d'entraînement transformé avec des fonctionnalités $ k $ (appelé n_components dans l'API). Il multiplie également $ V_k $ pour convertir l'ensemble de test $ X $.

X' = X V_k

** Remarque: ** La plupart des traitements LSA dans la littérature sur le traitement du langage naturel (NLP) et la recherche d'information (IR) doivent être sous la forme n_features x n_samples en permutant les axes de la matrice $ n $. Je vais. Nous présentons les LSA de différentes manières qui correspondent bien à l'API scicit-learn, mais les singularités trouvées sont les mêmes.

TruncatedSVD est très similaire à PCA, sauf qu'il fonctionne directement sur la matrice échantillon $ X $ au lieu de la matrice covariante. En soustrayant la moyenne de $ X $ dans la direction de la colonne (par entité) de la quantité d'entités, le SVD tronqué résultant sur la matrice est équivalent à PCA. En pratique, cela ne densifie pas la matrice «scipy.sparse», car le convertisseur SVD tronqué peut remplir la mémoire même pour des collections de documents de taille moyenne. Moyens d'accepter. Le convertisseur TruncatedSVD fonctionne avec n'importe quelle matrice de fonctionnalités (clairsemée), mais son utilisation avec la matrice tf-idf est recommandée par rapport au nombre de fréquences non traitées des paramètres de traitement LSA / document. En particulier, pour compenser les fausses hypothèses de LSA sur les données textuelles, la mise à l'échelle sous-linéaire et la fréquence inverse du document doivent être activées pour rapprocher les valeurs des caractéristiques de la distribution gaussienne (sublinear_tf = True, ʻuse_idf =". Vrai`).

• Exemple:
• Clustering des documents texte à l'aide de k-means
• Les références:
• Christopher D. Manning, Prabhakar Raghavan et Hinrich Schütze (2008), Cambridge University Press, Chapitre 18: Matrix Decomposition and Latent Semantic Indexing .pdf)

2.5.3. Apprentissage du dictionnaire

2.5.3.1. Codage fragmentaire avec dictionnaire pré-calculé

SparseCoder L'objet est un signal précalculé fixe, tel qu'une base d'ondelettes discrète. Un estimateur qui peut être utilisé pour convertir en jointures linéaires éparses à partir d'un dictionnaire. Par conséquent, cet objet n'implémente pas la méthode «fit». Cette conversion devient un problème de codage clairsemé. Trouver une représentation des données sous la forme d'une jointure linéaire d'aussi peu d'atomes de dictionnaire que possible. Toutes les variantes d'apprentissage du dictionnaire implémentent les méthodes de transformation suivantes qui peuvent être contrôlées via le paramètre d'initialisation transform_method.

• Poursuite de l'appariement orthogonal (OMP: Orthogonal Matching Pursuit)
• Régression d'angle minimum (Régression d'angle minimum)
• Lasso calculé par régression d'angle minimum
• Lasso utilisant la descente de coordonnées (Lasso) (Lasso)
• Seuil

Les seuils sont très rapides, mais ils ne peuvent pas être reconstruits avec précision. Ils se sont révélés utiles dans la littérature pour les travaux de classification. Pour les tâches de reconstruction d'image, le suivi de correspondance orthogonale fournit la reconstruction la plus précise et la plus impartiale. L'objet d'apprentissage dictionnaire offre la possibilité de séparer les valeurs positives et négatives dans le résultat d'un codage fragmenté via le paramètre split_code. Il s'agit d'une formation par dictionnaire pour extraire les fonctionnalités utilisées pour l'apprentissage supervisé afin que l'algorithme d'apprentissage puisse attribuer différents poids allant des charges positives aux charges négatives correspondant à la charge négative d'un atome particulier Ceci est utile lors de l'utilisation. Le code fractionné pour un échantillon a une longueur de 2 * n_components et est créé à l'aide des règles suivantes: Tout d'abord, le code normal de longueur «n_composants» est calculé. La première entrée n_components pour split_code est alors remplie avec la partie positive du vecteur de code régulier. La seconde moitié du code fractionné est remplie avec la partie négative du vecteur de code avec uniquement des signes positifs. Par conséquent, split_code n'est pas négatif.

• Exemple:
• Codage épars avec dictionnaire pré-calculé

2.5.3.2. Apprentissage général du dictionnaire

L'apprentissage par dictionnaire (DictionaryLearning) consiste à encoder de manière clairsemée les données correspondantes. C'est un problème de décomposition matricielle qui correspond à la recherche d'un dictionnaire (généralement excessif) qui fonctionne bien avec. Représenter les données comme une combinaison diluée d'atomes du dictionnaire trop complet suggère le travail des principales zones visuelles des mammifères. En conséquence, l'apprentissage du dictionnaire appliqué aux correctifs d'image s'est avéré donner de bons résultats dans les tâches de traitement d'image telles que l'achèvement, la réparation et l'élimination du bruit d'image, ainsi que les tâches de reconnaissance surveillées. L'apprentissage du dictionnaire est un problème d'optimisation qui est résolu en mettant à jour le code fragmenté d'une manière alternative et en modifiant le dictionnaire pour l'adapter au mieux au code fragmenté comme solution au problème de lasso multiple. ..

(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2}
             ||X-UV||_2^2+\alpha||U||_1 \\

             \text{subject to\,} & ||V_k||_2 = 1 \text{ for all }
             0 \leq k < n_{atoms}

Après adaptation à un dictionnaire à l'aide de ces étapes, la transformation est une étape de codage simple qui partage la même implémentation avec tous les objets d'apprentissage du dictionnaire (Sparse Coding with Pre-Calculated Dictionaries) (http: // Voir scikit-learn.org/0.18/modules/decomposition.html#sparsecoder). L'image suivante montre comment le dictionnaire a été formé à partir d'un patch d'image de 4 x 4 pixels extrait d'une partie de l'image du visage du raigma.

• Exemple:
• Suppression du bruit d'image à l'aide de l'apprentissage par dictionnaire
• Les références:
• "Apprendre un dictionnaire en ligne pour le codage clairsemé" J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009

2.5.3.3. Apprentissage du dictionnaire par mini-lots

MiniBatchDictionaryLearning est un algorithme d'apprentissage de dictionnaire plus rapide adapté aux grands ensembles de données. Cependant, il implémente une version moins précise. Par défaut, MiniBatchDictionaryLearning divise les données en mini-lots et les optimise en ligne en faisant circuler le mini-lot un nombre spécifié d'itérations. Cependant, il n'implémente pas un état arrêté pour le moment. L'estimateur implémente également partial_fit. Cela ne mettra à jour le dictionnaire qu'une seule fois dans un mini-lot. Cela peut être utilisé pour l'apprentissage en ligne si les données ne sont pas facilement disponibles depuis le début ou si les données ne tiennent pas dans la mémoire.

** Clustering pour l'apprentissage du dictionnaire **

Notez que le clustering peut être un bon proxy pour l'apprentissage des dictionnaires lors de l'utilisation de l'apprentissage par dictionnaire pour extraire des expressions (par exemple dans le cas d'un codage clairsemé). Par exemple, MiniBatchKMeans L'estimateur est efficace en calcul et la méthode partial_fit Effectuer un apprentissage en ligne en utilisant.

• Exemple: [Apprentissage en ligne du dictionnaire des parties du visage](http://scikit-learn.org/0.18/auto_examples/cluster/plot_dict_face_patches.html#sphx-glr-auto-examples-cluster-plot-dict-face-patches -py)

2.5.4. Analyse factorielle

Dans l'apprentissage non supervisé, l'ensemble de données est $ X = \ {x_1, x_2, \ dots, x_n Il n'y a que } $. Comment cet ensemble de données peut-il être décrit mathématiquement? Dans un modèle de variable latente continue très simple, $ X $ est

x_i = W h_i + \mu + \epsilon

Le vecteur $ h \ _i $ n'est pas observé et est donc appelé "latent". $ ε $ est considéré comme un terme de bruit distribué selon une distribution gaussienne de moyenne 0 et de covariance $ \ Psi $ (ie $ \ epsilon \ sim \ mathcal {N} (0, \ Psi)) $). $ μ $ est un vecteur de décalage arbitraire. Un tel modèle est appelé "génératif" car il décrit comment $ x \ _i $ est généré à partir de $ h \ _i $. Utiliser tous les $ x \ _i $ comme colonnes pour créer la matrice $ \ mathbf {X} $ et tous les $ h_i $ comme colonnes dans la matrice $ \ mathbf {H} $ (bien défini) Vous pouvez écrire (en utilisant $ \ mathbf {M} $ et $ \ mathbf {E} $) comme suit:

\mathbf{X} = W \mathbf{H} + \mathbf{M} + \mathbf{E}

En d'autres termes, nous avons décomposé la matrice $ \ mathbf {X} $. Étant donné $ h_i $, l'équation ci-dessus signifie automatiquement l'interprétation probabiliste suivante:

p(x_i|h_i) = \mathcal{N}(Wh_i + \mu, \Psi)

Pour le modèle de probabilité parfait, nous avons également besoin d'une distribution préalable pour la variable latente $ h $. L'hypothèse la plus simple basée sur les bonnes caractéristiques de la distribution gaussienne est $ h \ sim \ mathcal {N} (0, \ mathbf {I}) $. Cela produit une distribution gaussienne comme la distribution marginale de $ x $:

p(x) = \mathcal{N}(\mu, WW^T + \Psi)

Or, sans autre hypothèse, l'idée d'avoir la variable latente $ h $ serait superflue. $ x $ peut être entièrement modélisé avec la moyenne et la covariance. Nous devons imposer une structure plus spécifique à l'un de ces deux paramètres. Une simple hypothèse supplémentaire concerne la structure de la covariance d'erreur $ \ Psi $:

• $ \ Psi = \ sigma ^ 2 \ mathbf {I} $: Cette hypothèse conduit à un modèle probabiliste de l'ACP.
• $ \ Psi = diag (\ psi_1, \ psi_2, \ dots, \ psi_n) $: Ce modèle est un modèle statistique classique Factor Analysis Factor Analysis Il s'appelle /generated/sklearn.decomposition.FactorAnalysis.html#sklearn.decomposition.FactorAnalysis). La matrice W est parfois appelée «matrice de chargement factoriel».

Les deux modèles estiment essentiellement une distribution gaussienne avec une matrice de covariance de faible rang. Les deux modèles sont probabilistes et peuvent être intégrés dans des modèles plus complexes. Par exemple, une combinaison d'analyses factorielles. Modèles très différents (par exemple FastICA lorsque des probabilités a priori non gaussiennes sur des variables latentes sont supposées .decomposition.FastICA)) est obtenu. L'analyse factorielle place un composant similaire (la colonne dans sa matrice de chargement) dans PCA. Peut être généré. Cependant, il n'est pas possible de faire une description générale de ces composants (par exemple, s'ils sont orthogonaux ou non).

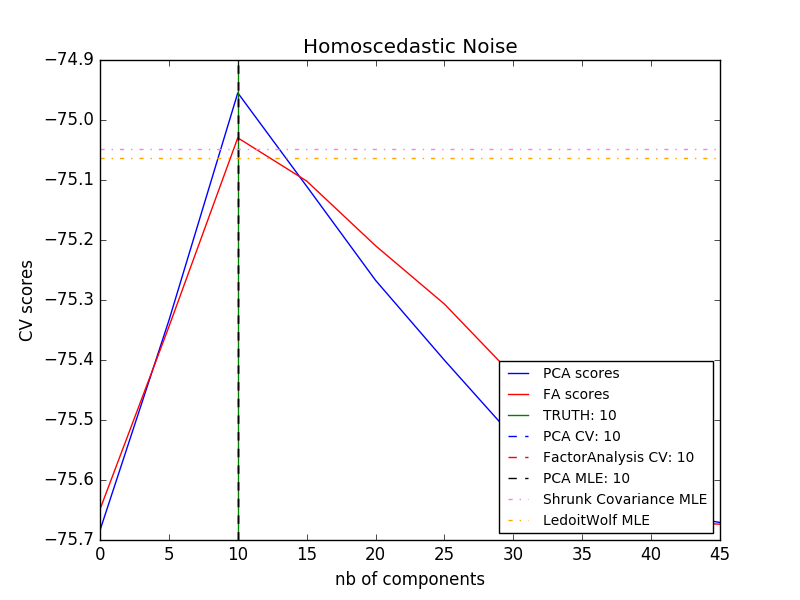
Le principal avantage de l'analyse factorielle par rapport à PCA est dans toutes les directions de l'espace d'entrée. La possibilité de modéliser la dispersion individuellement (bruit hétéroscédastique).

Cela permet une meilleure sélection de modèle que l'ACP probabiliste en présence de bruit anisotrope.

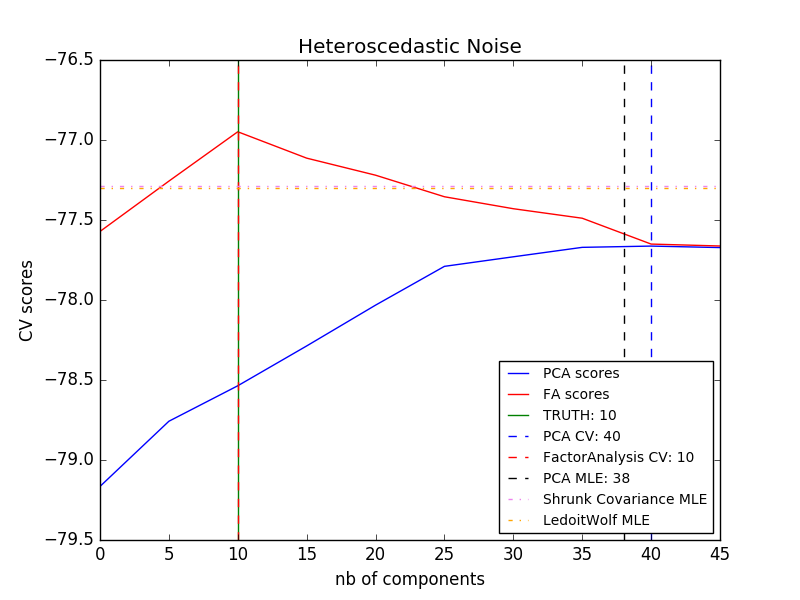
• Exemple:
• [Sélection du modèle par PCA probabiliste et analyse factorielle (FA)](http://scikit-learn.org/0.18/auto_examples/decomposition/plot_pca_vs_fa_model_selection.html#sphx-glr-auto-examples-decomposition-plot-pca- vs-fa-model-selection-py)

2.5.5. Analyse des composants indépendants (ICA)

L'analyse indépendante des composants sépare les signaux multivariés en sous-composants additifs au maximum indépendants. FastICA Implémenté dans scikit-learn en utilisant l'algorithme. Typiquement, ICA est utilisé pour séparer les signaux superposés, pas pour réduire la dimensionnalité. Le modèle ICA ne contient pas de terme de bruit, donc un blanchiment doit être appliqué pour que le modèle soit correct. Cela peut être fait en interne en utilisant l'argument whiten ou manuellement en utilisant PCA ou l'une de ses variantes. Il est classiquement utilisé pour séparer les signaux mixés (un problème appelé séparation aveugle de la source sonore), comme dans l'exemple ci-dessous.

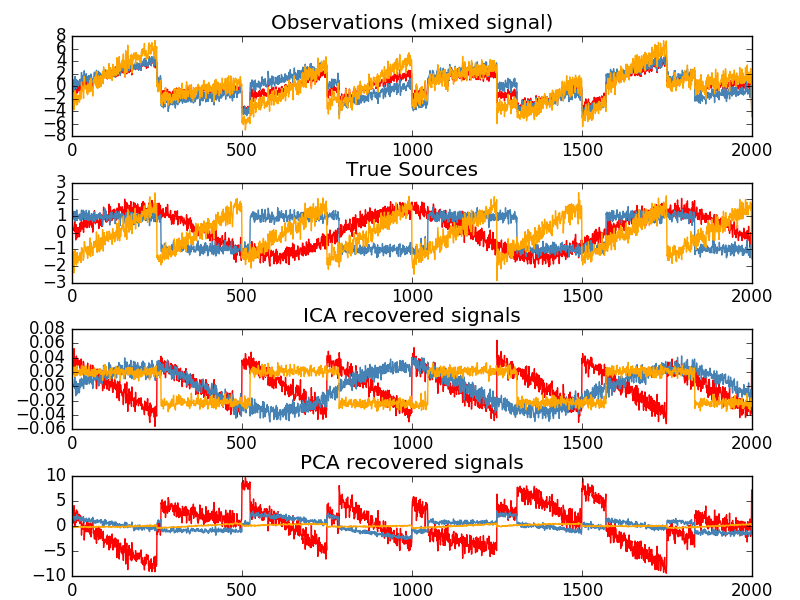
L'ICA peut également être utilisé comme une autre décomposition non linéaire qui trouve des composants clairsemés.

• Exemple:
• [Séparation des sources aveugles à l'aide de FastICA](http://scikit-learn.org/0.18/auto_examples/decomposition/plot_ica_blind_source_separation.html#sphx-glr-auto-examples-decomposition-plot-ica-blind-source- séparation-py)
• Groupe de points 2D FastICA
• Face Dataset Decomposition

2.5.6. Décomposition matricielle non négative (NMF ou NNMF)

Original

2.5.6.1. NMF avec norme Frobenius

NMF est une décomposition qui suppose que les données et les composants ne sont pas négatifs. Une approche alternative. Si la matrice de données ne contient pas de valeurs négatives, vous pouvez insérer NMF au lieu de PCA ou de ses variantes. En optimisant la distance $ d $ entre $ X $ et le produit matriciel $ WH $, nous trouvons la décomposition de l'échantillon $ X $ en deux éléments non négatifs, $ W $ et $ H $. La fonction de distance la plus largement utilisée est la norme de Frobenius au carré, qui est une extension évidente de la matrice de distance euclidienne.

d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{\mathrm{Fro}}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2

Contrairement à l'ACP, la représentation du vecteur est obtenue de manière additive en superposant les composantes sans soustraction. Un tel modèle additif est utile pour représenter des images et du texte. Dans [Hoyer, 04], il a été observé que NMF produit une représentation à base de parties d'un jeu de données, qui, lorsqu'elle est soigneusement contrainte, fournit un modèle interprétable. L'exemple suivant montre 16 composants dilués trouvés par NMA par rapport à une surface spécifique PCA à partir d'une image du jeu de données de visage Olivetti. L'attribut ʻinitdétermine la méthode d'initialisation appliquée. Cela a un impact significatif sur les performances de la méthode. NMF implémente la méthode de décomposition de double singularité non négative (NNDSVD). NNDSVD est basé sur deux processus SVD qui se rapprochent de la matrice de données, et les autres sections positives similaires du coefficient SVD partiel résultant tirent parti de la nature algébrique de la matrice de rang unitaire. L'algorithme de base NNDSVD convient à la décomposition en facteurs clairsemés. Pour la haute densité, ses variantes NNDSVDa (tous les zéros sont mis égaux à la moyenne de tous les éléments des données) et NNDSVDar (où zéro est une perturbation aléatoire plus petite que la moyenne des données divisée par 100). Est réglé sur) est recommandé. NMF peut également être initialisé avec une matrice aléatoire non négative correctement mise à l'échelle en définissant ʻinit = "random". Vous pouvez également passer une graine entière ou RandomState à random_state pour contrôler la reproductibilité. NMF vous permet d'ajouter des fonctions L1 et L2 à la fonction de perte pour normaliser le modèle. L2 a priori utilise la norme de Frobenius et L1 a priori la norme élément unité L1. Comme ElasticNet, la combinaison de L1 et L2 est contrôlée par le paramètre l1_ratio ($ \ rho ), et la force de la régularisation est contrôlée par le paramètre ʻalpha` ( \ alpha $). Les termes a priori sont:

\alpha \rho ||W||_1 + \alpha \rho ||H||_1
+ \frac{\alpha(1-\rho)}{2} ||W||_{Fro} ^ 2
+ \frac{\alpha(1-\rho)}{2} ||H||_{Fro} ^ 2

La fonction objectif normalisée est:

\frac{1}{2}||X - WH||_{Fro}^2
+ \alpha \rho ||W||_1 + \alpha \rho ||H||_1
+ \frac{\alpha(1-\rho)}{2} ||W||_{Fro} ^ 2
+ \frac{\alpha(1-\rho)}{2} ||H||_{Fro} ^ 2

NMF normalise à la fois W et H. La fonction non_negative_factorization a un contrôle plus fin sur les attributs de normalisation et peut normaliser W, H seulement, ou les deux.

• Exemple:
• Face Dataset Decomposition
• [Extraction de sujets à l'aide de la décomposition de facteurs matriciels non négatifs et de l'attribution potentielle de jilliclets](http://scikit-learn.org/0.18/auto_examples/applications/topics_extraction_with_nmf_lda.html#sphx-glr-auto-examples-applications-topics- extraction-avec-nmf-lda-py)
• Les références:
• "Apprendre la partie d'un objet par décomposition matricielle non négative" D. Lee, S. Seung, 1999
• "Décomposition factorielle de la matrice non négative avec contrainte de parcimonie" P. Hoyer, 2004
• "Méthode du gradient de projection pour la décomposition matricielle non négative" C.-J. Lin, 2007
• "Initialisation basée sur SVD: début de la décomposition de la matrice non négative" C. Boutsidis, E. Gallopoulos, 2008
• "Algorithme local rapide pour la décomposition de matrice et tenseur non négative à grande échelle" A. Cichocki, P. Anh-Huy, 2009

2.5.7. Méthode d'attribution de direction potentielle (LDA)

Original

L'allocation de dirichlet latent est un modèle probabiliste génératif pour collecter des ensembles de données discrets tels que des corpus de texte. C'est également le modèle de sujet utilisé pour découvrir des sujets abstraits à partir d'une collection de documents. Le modèle graphique LDA est un modèle de bassin à trois niveaux.

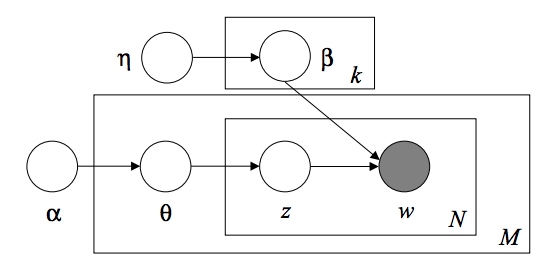
Lors de la modélisation d'un corpus de texte, le modèle suppose le processus de génération suivant pour un corpus avec un document D et une rubrique K.

• Pour chaque sujet $ k $, $ \ beta_k \ sim Dirichlet (\ eta), : k = 1 ... K $
• Pour chaque document $ d $, $ \ theta_d \ sim Dirichlet (\ alpha), : d = 1 ... D $
• Pour chaque mot $ i $ du document $ d $:
• Dessiner l'index du sujet $ z_ {di} \ sim Multinomial (\ theta_d) $
• Représente le mot observé $ w_ {ij} \ sim Multinomial (beta_ {z_ {di}}.) $

Pour l'estimation des paramètres, la distribution a posteriori est:

p(z, \theta, \beta |w, \alpha, \eta) =
  \frac{p(z, \theta, \beta|\alpha, \eta)}{p(w|\alpha, \eta)}

Comme le dos est gênant, la méthode bayésienne Variante utilise une distribution plus simple pour approximer $ q (z, \ theta, \ beta | \ lambda, \ phi, \ gamma) $ et leurs paramètres variant $ \ lambda, \ phi, \ gamma $ sont optimisés pour maximiser la limite inférieure des preuves (ELBO).

log\: P(w | \alpha, \eta) \geq L(w,\phi,\gamma,\lambda) \overset{\triangle}{=}
  E_{q}[log\:p(w,z,\theta,\beta|\alpha,\eta)] - E_{q}[log\:q(z, \theta, \beta)]

Maximiser ELBO est un Kullback-Leibler entre $ q (z, \ theta, \ beta) $ et le vrai postérieur $ p (z, \ theta, \ beta | w, \ alpha, \ eta) $ Équivaut à minimiser la différence de (KL).

LatentDirichletAllocation implémente la variante en ligne de l'algorithme bayésien pour les mises à jour en ligne et par lots. Prend en charge les deux méthodes. La méthode par lots met à jour la variable variable après avoir transmis chaque chemin complet aux données, tandis que la méthode en ligne met à jour la variable variable à partir du point de données du mini-lot. ** Remarque: ** La méthode en ligne est garantie de converger vers le point optimal local, mais la qualité et la vitesse de convergence du point optimal peuvent dépendre de la taille du mini-lot et des attributs associés au paramètre de vitesse d'apprentissage. Lorsque LatentDirichletAllocation est appliqué à la matrice "Document-Termes", la matrice est décomposée en une matrice "Topic-Terms" et une matrice "Document-Topic". La matrice "topic-terms" est stockée en tant que "components_" dans le modèle, mais vous pouvez calculer la matrice "document-topic" avec la méthode transform. LatentDirichletAllocation implémente également la méthode partial_fit. Ceci est utilisé lorsque les données sont récupérées en continu.

• Exemple:
• [Extraction de sujets à l'aide de la décomposition de facteurs matriciels non négatifs et de l'attribution potentielle de jilliclets](http://scikit-learn.org/0.18/auto_examples/applications/topics_extraction_with_nmf_lda.html#sphx-glr-auto-examples-applications-topics- extraction-avec-nmf-lda-py)
• Les références:
• Méthode d'attribution potentielle de Diricle D. Bray, A. N, M. Jordan, 2003
• Apprentissage en ligne pour la méthode d'attribution potentielle de Diricle M. Hoffman, D.Blei, F.Bach, 2010
• Inférence de variante probabiliste M. Hoffman, D.Blei, C.Wang, J.Pasley, 2013

[Contenu du guide de l'utilisateur](http://qiita.com/nazoking@github/items/267f2371757516f8c168#2-%E6%95%99%E5%B8%AB%E3%81%AA%E3%81%97%E5 % AD% A6% E7% BF% 92)

© 2010 --2016, développeurs scikit-learn (licence BSD).