[PYTHON] [Français] scikit-learn 0.18 Guide de l'utilisateur 4.5. Projection aléatoire
google traduit http://scikit-learn.org/0.18/modules/random_projection.html [scikit-learn 0.18 User Guide 4. Dataset Conversion](http://qiita.com/nazoking@github/items/267f2371757516f8c168#4-%E3%83%87%E3%83%BC%E3%82%BF % E3% 82% BB% E3% 83% 83% E3% 83% 88% E5% A4% 89% E6% 8F% 9B)
4.5. Projection aléatoire
sklearn.random_projection Les modules sont une quantité contrôlée pour des temps de traitement plus rapides et des modèles plus petits Implémente un moyen simple et efficace de réduire la dimension des données en échangeant la précision de (comme une variance supplémentaire). Ce module implémente deux types de matrices aléatoires non structurées, la matrice aléatoire gaussienne et la matrice aléatoire Sparse. Les dimensions et la distribution de la matrice de projection aléatoire sont contrôlées pour préserver la distance appariée entre deux échantillons quelconques de l'ensemble de données. Par conséquent, la projection aléatoire est une bonne technique d'approximation pour les méthodes basées sur la distance.
- Les références:
- Sanjoy Das gupta. Expérience par projection aléatoire. Compte-rendu de la 16e réunion sur l'incertitude de l'intelligence artificielle (UAI'00), Craig Boutilier et Moisés Goldszmidt (dir.). Morgan Kaufmann Publishers Inc., San Francisco, Californie, États-Unis, 143-151.
- Ella Bingham et Heiki Mannilla 2001 [Projection aléatoire dans la réduction de dimension: application aux données image et texte](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.24.5135&rep=rep1&type = pdf) Conférence à la 7e Conférence internationale ACM SIGKDD sur la découverte des connaissances et l'exploration de données (KDD'01) ACM, New York, NY, USA, 245-250.
4.5.1. Supplément Johnson-Lindenstrauss
Le principal résultat théorique de l'efficacité de la projection aléatoire est Johnson Lindenstrauss Supplement (citant Wikipedia).
En mathématiques, l'annexe de Johnson-Lindenstrauss est le résultat d'un encastrement à faible distorsion de points dans un espace euclidien de dimension élevée à faible. Le supplément indique qu'un petit ensemble de points dans un espace dimensionnel plus élevé peut être intégré dans un espace dimensionnel beaucoup plus bas de sorte que la distance entre les points soit largement préservée. La carte utilisée pour l'intégration est au moins Lipschitz et peut également être considérée comme une projection orthodoxe.
[sklearn.random_projection.johnson_lindenstrauss_min_dim](http://scikit-learn.org/0.18/modules/generated/sklearn.random_projection.johnson_lindenstrauss_min_dim.html#sklearn.random_projection.johnson_linden.random_projection.johnson_dim.html#sklearn.random_projection. Il estime de manière prudente la taille minimale du sous-espace artificiel et garantit la distorsion bornée introduite par la projection aléatoire.
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
663
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894, 9868, 11841])
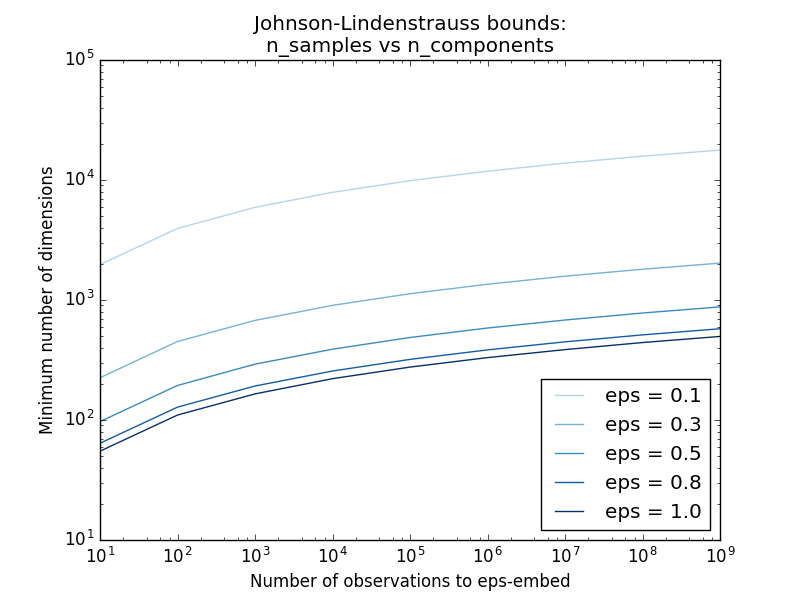
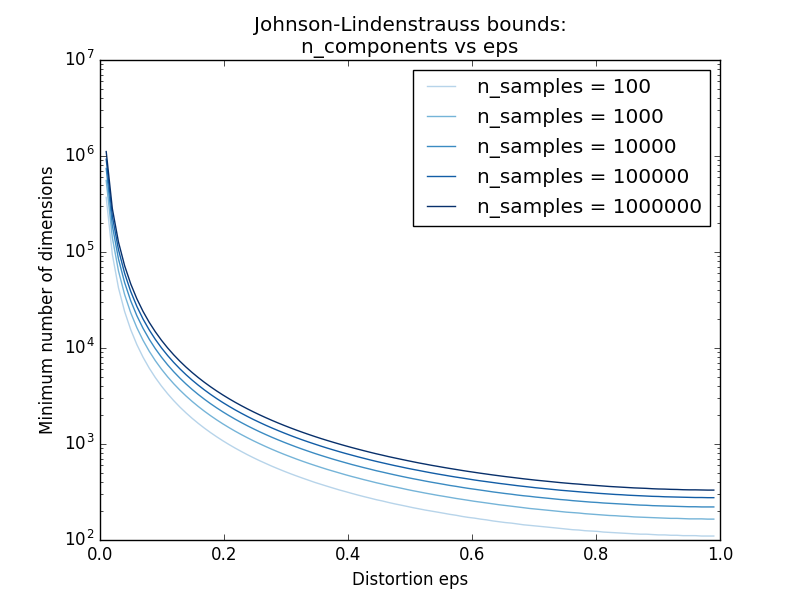
- Exemple:
- Voir Johnson-Lindenstrauss pour un commentaire théorique sur l'annexe et Johnson-Lindenstrauss pour l'inclusion de projection aléatoire pour une vérification empirique à l'aide de matrices aléatoires clairsemées.
- Les références:
- Sanjoy Das gupta et Anupam Gupta, 1999. Preuve de base du supplément Johnson-Lindenstrauss.
4.5.2. Projection aléatoire gaussienne
sklearn.random_projection.GaussianRandomProjection projette l'espace d'entrée d'origine sur une matrice générée aléatoirement pour réduire les dimensions. Ici, les composants sont dérivés de la distribution suivante $ N (0, \ frac {1} {n_ {composants}}) $. Voici un petit extrait montrant comment utiliser le transformateur de projection aléatoire gaussien:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
4.5.3. Projection aléatoire éparse
sklearn.random_projection.SparseRandomProjection est l'entrée d'origine utilisant une matrice aléatoire clairsemée Réduisez les dimensions en projetant de l'espace.
La matrice aléatoire clairsemée est une alternative à la matrice de projection aléatoire gaussienne dense, qui garantit une qualité d'incorporation similaire, est plus efficace en mémoire et permet un calcul rapide des données projetées.
Si vous définissez s = 1 / densité, les éléments de la matrice aléatoire
\left\{
\begin{array}{c c l}
-\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\
0 &\text{with probability} & 1 - 1 / s \\
+\sqrt{\frac{s}{n_{\text{components}}}} & & 1 / 2s\\
\end{array}
\right.
Où $ n_ {\ text {components}} $ est la taille du sous-espace projeté. Par défaut, la densité des éléments non nuls est définie sur la densité minimale suivante recommandée par Ping Li et al. $ 1 / \ sqrt {n_ {\ text {features}}} $
Un petit extrait montrant comment utiliser la transformation de projection aléatoire clairsemée:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100,10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
- Les références:
- D. Achlioptas Projection aléatoire compatible avec la base de données: Johnson-Lindenstrauss et pièces binaires Science des systèmes informatiques 66 (2003) 671-687
- Ping Li, Trevor J. Hastie et Kenneth W. Church 2006 [Projection aléatoire très clairsemée](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.62.585&rep=rep1&type= pdf) Conférence à la 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '06) ACM, New York, NY, USA, 287-296.
[scikit-learn 0.18 User Guide 4. Dataset Conversion](http://qiita.com/nazoking@github/items/267f2371757516f8c168#4-%E3%83%87%E3%83%BC%E3%82%BF % E3% 82% BB% E3% 83% 83% E3% 83% 88% E5% A4% 89% E6% 8F% 9B)
© 2010 --2016, développeurs scikit-learn (licence BSD).
Recommended Posts