[PYTHON] [Français] scikit-learn 0.18 Guide de l'utilisateur 3.3. Évaluation du modèle: quantifier la qualité de la prédiction
google traduit http://scikit-learn.org/0.18/modules/model_evaluation.html [scikit-learn 0.18 Guide de l'utilisateur 3. Sélection et évaluation du modèle](http://qiita.com/nazoking@github/items/267f2371757516f8c168#3-%E3%83%A2%E3%83%87%E3%83] À partir de% AB% E3% 81% AE% E9% 81% B8% E6% 8A% 9E% E3% 81% A8% E8% A9% 95% E4% BE% A1)
3.3. Évaluation du modèle: quantifier la qualité des prévisions
Il existe trois approches différentes pour évaluer la qualité des prévisions des modèles.
- ** Méthode de score de l'estimateur **: L'estimateur a une méthode de «score» qui fournit des métriques par défaut pour les problèmes destinés à être résolus. Ce n'est pas sur cette page, mais dans la documentation de chaque estimateur.
- ** Paramètres de notation **: outil d'évaluation de modèle ([model_selection.cross_val_score](http: // scikit-learn)) utilisant la validation croisée .org / 0.18 / modules / generated / sklearn.model_selection.cross_val_score.html # sklearn.model_selection.cross_val_score) et [model_selection.GridSearchCV](http://scikit-learn.org/0.18/modules/generated/sklearn.model_selection. GridSearchCV.html # sklearn.model_selection.GridSearchCV), etc.) repose sur une stratégie de notation interne. Pour cela, voir Paramètres de notation: Définition des règles d'évaluation du modèle (# 331-% E5% BE% 97% E7% 82% B9% E3% 83% 91% E3% 83% A9% E3% 83% A1% E3% 83% BC% E3% 82% BF% E3% 83% A2% E3% 83% 87% E3% 83% AB% E8% A9% 95% E4% BE% A1% E3% 83% AB% E3% Il est expliqué dans la section 83% BC% E3% 83% AB% E3% 81% AE% E5% AE% 9A% E7% BE% A9).
- ** Fonction métrique **: le module métrique implémente une fonction qui évalue les erreurs de prédiction dans un but précis. Ces métriques sont décrites en détail dans les sections sur les métriques de classification, les métriques de classement multi-étiquettes, les métriques de régression et les métriques de clustering.
Enfin, les évaluateurs fictifs sont utiles pour obtenir des valeurs de référence pour ces métriques pour la prédiction aléatoire.
- ** Voir: ** Métriques "par paires", pour les différences entre les échantillons et les estimations ou prédictions, voir les métriques par paires, l'affinité et les noyaux (http://scikit-learn.org/0.18/modules) Voir la section /metrics.html#metrics).
3.3.1. Paramètres de score: définition des règles d'évaluation du modèle
model_selection.GridSearchCV et [model_selection.cross_val_score](http: // scikit-learn) Pour la sélection et l'évaluation des modèles à l'aide d'outils tels que .org / 0.18 / modules / generated / sklearn.model_selection.cross_val_score.html # sklearn.model_selection.cross_val_score), le paramètre scoring qui contrôle les métriques appliquées aux métriques Utiliser.
3.3.1.1. Cas général: valeur prédéfinie
Pour les cas d'utilisation les plus courants, vous pouvez utiliser le paramètre scoring pour spécifier un objet de scoring. Le tableau ci-dessous montre toutes les valeurs possibles. Tous les objets scorer suivent la règle selon laquelle ** les valeurs de retour supérieures sont meilleures que les valeurs de retour inférieures **. Par conséquent, la distance entre le modèle et les données, telle que metrics.mean_squared_error La métrique que vous mesurez est disponible sous la forme neg_mean_squared_error, qui renvoie la valeur négative de la métrique.
| Scoring | Function | Comment |
|---|---|---|
| Classification | ||
| ‘accuracy’ | metrics.accuracy_score |
|
| ‘average_precision’ | metrics.average_precision_score |
|
| ‘f1’ | metrics.f1_score |
Pour les cibles binaires |
| ‘f1_micro’ | metrics.f1_score |
Micro moyennage |
| ‘f1_macro’ | metrics.f1_score |
Moyenne macro |
| ‘f1_weighted’ | metrics.f1_score |
moyenne pondérée |
| ‘f1_samples’ | metrics.f1_score |
Échantillon multi-étiquettes |
| ‘neg_log_loss’ | metrics.log_loss |
predict_probaBesoin de soutien |
| ‘precision’ etc. | metrics.precision_score |
Le suffixe est'f1'S'applique de la même manière que. |
| ‘recall’ etc. | metrics.recall_score |
Le suffixe est'f1'S'applique de la même manière que. |
| ‘roc_auc’ | metrics.roc_auc_score |
|
| Clustering | ||
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score |
|
| Revenir | ||
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error |
|
| ‘neg_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_median_absolute_error’ | metrics.median_absolute_error |
|
| ‘r2’ | metrics.r2_score |
Usage examples:
>>>
>>> from sklearn import svm, datasets
>>> from sklearn.model_selection import cross_val_score
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> clf = svm.SVC(probability=True, random_state=0)
>>> cross_val_score(clf, X, y, scoring='neg_log_loss')
array([-0.07..., -0.16..., -0.06...])
>>> model = svm.SVC()
>>> cross_val_score(model, X, y, scoring='wrong_choice')
Traceback (most recent call last):
ValueError: 'wrong_choice' is not a valid scoring value. Valid options are ['accuracy', 'adjusted_rand_score', 'average_precision', 'f1', 'f1_macro', 'f1_micro', 'f1_samples', 'f1_weighted', 'neg_log_loss', 'neg_mean_absolute_error', 'neg_mean_squared_error', 'neg_median_absolute_error', 'precision', 'precision_macro', 'precision_micro', 'precision_samples', 'precision_weighted', 'r2', 'recall', 'recall_macro', 'recall_micro', 'recall_samples', 'recall_weighted', 'roc_auc']
- ** Remarque: ** Les valeurs répertoriées par l'exception ValueError correspondent aux fonctions qui mesurent la précision prédictive décrites dans la section suivante. Les objets scorer pour ces fonctions sont stockés dans le dictionnaire sklearn.metrics.SCORERS.
3.3.1.2. Définition des stratégies de notation à partir des fonctions métriques
Le module sklearn.metric expose également un ensemble de fonctions simples qui mesurent les valeurs mesurées et les erreurs de prédiction en fonction d'une prédiction:
- Les fonctions se terminant par
_scorerenvoient la valeur à maximiser. - Les fonctions se terminant par
_errorou_lossrenvoient une valeur pour revenir à la valeur minimale. Lors de la conversion en objet scorer à l'aide de make_scorer, le paramètregreater_is_betterEst défini sur False (True par défaut, voir la description des paramètres ci-dessous). Les mesures pouvant être utilisées dans diverses tâches d'apprentissage automatique sont décrites en détail dans les sections ci-dessous.
De nombreuses métriques peuvent nécessiter des paramètres supplémentaires tels que fbeta_score Par conséquent, il n'y a pas de nom à utiliser comme valeur de score. Dans de tels cas, vous devez générer un objet de notation approprié. Le moyen le plus simple de générer un objet appelable est d'utiliser make_scorer Le chemin. Cette fonction transforme la métrique en un objet appelable qui peut être utilisé pour l'évaluation du modèle.
Un cas d'utilisation typique consiste à encapsuler une fonction métrique existante à partir d'une bibliothèque avec une valeur autre que celle par défaut pour un paramètre, tel que le paramètre beta de la fonction fbeta_score.
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]}, scoring=ftwo_scorer)
Le deuxième cas d'utilisation est de créer un objet scorer complètement personnalisé à partir d'une simple fonction Python en utilisant make_scorer qui peut prendre certains paramètres:
--Fonction Python à utiliser (my_custom_loss_func dans l'exemple ci-dessous)
--Si la fonction python renvoie un score (par défaut greater_is_better = True) ou une perte ( greater_is_better = False). En cas de perte, l'objet scorer invalide la sortie de la fonction python et le scorer renvoie une valeur plus élevée pour un meilleur modèle.
- Métriques de classification uniquement: indique si la fonction Python que vous avez fournie nécessite une certitude de décision continue (
needs_threshold = True) La valeur par défaut est False. - Paramètres supplémentaires tels que bêta et étiquettes pour f1_score.
L'exemple suivant crée un scorer personnalisé et utilise le paramètre «greater_is_better».
>>> import numpy as np
>>> def my_custom_loss_func(ground_truth, predictions):
... diff = np.abs(ground_truth - predictions).max()
... return np.log(1 + diff)
...
>>> # loss_func est mon_custom_loss_Désactive la valeur de retour de func.
>>> #C'est le terrain_np s'il y a une valeur de vérité et la prédiction définie ci-dessous.log(2)、0.Ce sera 693.
>>> loss = make_scorer(my_custom_loss_func, greater_is_better=False)
>>> score = make_scorer(my_custom_loss_func, greater_is_better=True)
>>> ground_truth = [[1, 1]]
>>> predictions = [0, 1]
>>> from sklearn.dummy import DummyClassifier
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf = clf.fit(ground_truth, predictions)
>>> loss(clf,ground_truth, predictions)
-0.69...
>>> score(clf,ground_truth, predictions)
0.69...
3.3.1.3. Mise en œuvre de l'objet de notation original
Vous pouvez générer un scoreur de modèle plus flexible en créant votre propre objet de scoring à partir de zéro sans utiliser la fabrique make_scorer. Pour que l'objet appelable soit un marqueur, il doit respecter le protocole spécifié dans les deux règles suivantes.
--Peut être appelé avec (estimator, X, y). ʻEstimatorest le modèle à évaluer,X est les données de validation et y est la cible mesurée de X(avec l'enseignant) ouAucun` (sans l'enseignant).
- Reportez-vous à «y» et renvoie un nombre à virgule flottante qui quantifie la qualité prédite de «l'estimateur» sur «X». Encore une fois, plus le nombre est élevé, mieux c'est, par convention, donc si le marqueur renvoie une perte, vous devez invalider cette valeur.
3.3.2. Métrique de classification
sklearn.metrics Le module implémente plusieurs fonctions de perte, de score et d'utilité pour mesurer les performances de classification Faire. Certaines mesures peuvent nécessiter une estimation probabiliste de la classe positive, des valeurs de confiance ou des valeurs de détermination binaire. Dans la plupart des implémentations, le paramètre sample_weight peut être utilisé pour permettre à chaque échantillon d'apporter une contribution pondérée au score global.
Ceux-ci sont limités à la classification binaire:
| matthews_corrcoef(y_true、y_pred [、...]) | Coefficient de corrélation de Matthews de classe binaire(MCC) |
| precision_recall_curve(y_true、probas_pred) | Taux d'adaptation à divers seuils de probabilité-Calculer les paires de rappel |
| roc_curve(y_true、y_score [、pos_label、...]) | Caractéristiques de fonctionnement du récepteur(ROC) |
Ceux-ci fonctionnent également en multi-classes:
| cohen_kappa_score(y1、y2 [、labels、weights]) | Cohen's kappa: statistiques qui mesurent les accords entre annotateurs. |
| confusion_matrix(y_true、y_pred [、labels、...]) | Calculer une matrice de confusion pour évaluer l'exactitude de la classification |
| hinge_loss(y_true、pred_decision [、labels、...]) | Perte de charnière moyenne(Dénormalisé) |
Ceux-ci fonctionnent également pour les multi-étiquettes:
| accuracy_score(y_true、y_pred [、normalize、...]) | Score de classification de la précision. |
| classification_report(y_true、y_pred [、...]) | Créer un rapport texte affichant les métriques de classification clés |
| f1_score(y_true、y_pred [、labels、...]) | Calculez le score F1. Ceci est également appelé un score F équilibré ou F majeur |
| fbeta_score(y_true、y_pred、beta [、labels、...]) | Calculer le score F Beta |
| hamming_loss(y_true、y_pred [、labels、...]) | Calculez la perte moyenne de bourdonnement. |
| jaccard_similarity_score(y_true、y_pred [、...]) | Score de similarité Jaccard |
| log_loss(y_true、y_pred [、eps、normalize、...]) | Perte de journal, également appelée perte logistique ou perte d'entropie croisée. |
| precision_recall_fscore_support(y_true、y_pred) | Taux de conformité, taux de rappel, F de chaque classe-Calculer la mesure et le support |
| precision_score(y_true、y_pred [、labels、...]) | Calculez la précision |
| recall_score(y_true、y_pred [、labels、...]) | Calculer le rappel |
| zero_one_loss(y_true、y_pred [、normalize、...]) | Aucune perte de classification. |
Ceux-ci fonctionnent avec binaire et multi-label (pas multi-classes)
| average_precision_score(y_true、y_score [、...]) | Précision moyenne à partir du score prévu(AP) |
| roc_auc_score(y_true、y_score [、average、...]) | Aire sous la courbe à partir du score prédit(AUC) |
Les sous-sections suivantes décrivent chacune de ces fonctions et préviennent certaines notes sur les définitions d'API et de métriques courantes.
3.3.2.1. Du binaire au multi-classes et multi-étiquettes
Fondamentalement, certaines métriques sont définies pour la tâche de classification binaire ([f1_score](http://scikit-learn.org/0.18/modules/generated/sklearn.metrics.f1_score.html#sklearn. metrics.f1_score), roc_auc_score. Dans de tels cas, par défaut, seules les étiquettes positives sont évaluées et la classe positive est étiquetée 1 (bien qu'elle puisse être configurée avec le paramètre pos_label).
Lors de l'extension d'une métrique binaire à un problème multi-classe ou multi-étiqueté, les données sont traitées comme un ensemble de problèmes binaires (un par classe). Il existe plusieurs façons de faire la moyenne des calculs de métriques binaires sur un ensemble de classes, ce qui est utile dans certains scénarios. Si possible, vous devez choisir entre ceux-ci en utilisant le paramètre ʻaverage`.
--` "macro" "calcule la moyenne des métriques binaires et donne à chaque classe des poids égaux. Néanmoins, pour les problèmes où les classes peu fréquentes sont importantes, la moyenne des macros peut être un moyen de mettre l'accent sur les performances. D'un autre côté, l'hypothèse selon laquelle toutes les classes sont également importantes n'est souvent pas vraie, de sorte que les moyennes macro surestiment généralement les performances médiocres dans les classes rares.
- «pondérés» «Les déséquilibres de classe sont« pondérés »en calculant la moyenne des métriques binaires pondérées par la présence du score de chaque classe dans un véritable échantillon de données.
-
"micro" "contribue également à la métrique globale pour chaque paire de classes d'échantillon (sauf pour les résultats de poids d'échantillon). Au lieu de faire la somme des mesures par classe, additionnez les dividendes et les diviseurs qui composent les mesures par classe pour calculer le quotient global. La micro-moyenne peut avoir la priorité dans les paramètres multi-étiquettes, y compris la classification multi-classes qui ignore de nombreuses classes. -"samples" ʻapplique uniquement aux problèmes multi-étiquettes. Au lieu de cela, il calcule les métriques de classe vraies et prédites pour chaque échantillon de données d'évaluation et renvoie sa moyenne (pondérée par «sample_weight»). --Sélectionner ʻaverage = None` renvoie un tableau contenant les scores de chaque classe.
Les données multi-classes sont fournies sous la forme d'un tableau d'étiquettes de classe métriquement comme une cible binaire, tandis que les données multi-étiquettes sont la cellule «[i, j» si l'échantillon «i» a l'étiquette «j». ] `Renvoie la valeur 1 dans le cas contraire.
3.3.2.2. Score d'exactitude
precision_score La fonction est un pourcentage prédictif précis (par défaut) ou un compte (normaliser" = False) est calculé.
Pour la classification multi-étiquettes, cette fonction renvoie un sous-ensemble de précision. Si l'ensemble complet d'étiquettes prédites dans l'échantillon correspond exactement à l'ensemble réel d'étiquettes, la précision du sous-ensemble est de 1,0. Sinon, c'est 0,0.
\texttt{accuracy}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} 1(\hat{y}_i = y_i)
Où $ 1 (x) $ est la fonction d'indicateur (https://en.wikipedia.org/wiki/Indicator_function).
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
>>> accuracy_score(y_true, y_pred, normalize=False)
2
Pour multi-étiquettes avec indicateur d'étiquette binaire:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5
--Exemple:
- Test de l'importance des scores de classification en séquence dans l'exemple d'utilisation des scores de précision en utilisant la séquence dans un ensemble de données (http://scikit-learn.org/0.18/auto_examples/feature_selection/plot_permutation_test_for_classification.html#sphx-glr Voir (-auto-examples-feature-selection-plot-permutation-test-for-classification-py).
3.3.2.3. Coefficient Kappa
La fonction cohen_kappa_score est le [coefficient Kappa](https: //en.wikipedia. org / wiki / Cohen% 27s_kappa) est calculé. Cette échelle vise à comparer l'étiquetage de différents commentateurs humains. Le score κ (voir docstring) est un nombre compris entre -1 et 1. Les scores supérieurs à 8 sont généralement considérés comme de bons résultats. En dessous de zéro, aucun accord (étiquette pratiquement aléatoire) Le score κ peut être calculé pour des problèmes binaires ou multiclasses, mais pas pour des problèmes à étiquettes multiples (sauf si vous calculez manuellement le score par étiquette) et pour deux annotations ou plus.
>>> from sklearn.metrics import cohen_kappa_score
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> cohen_kappa_score(y_true, y_pred)
0.4285714285714286
3.3.2.4. Matrice de confusion
confusion_matrix La fonction est [Confusion Matrix](https: //en.wikipedia. Évaluez la précision de la classification en calculant (org / wiki / Confusion_matrix). Par définition, l'entrée de la matrice de confusion $ i, j $ est le nombre réel d'observations pour le groupe $ i $, mais devrait appartenir au groupe $ j $. Voici un exemple:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
Ceci est une représentation visuelle d'une telle matrice de confusion (cette figure est la matrice de confusion](http://scikit-learn.org/0.18/auto_examples/model_selection/plot_confusion_matrix.html#sphx-glr-auto-examples- Un exemple de model-selection-plot-confusion-matrix-py)).
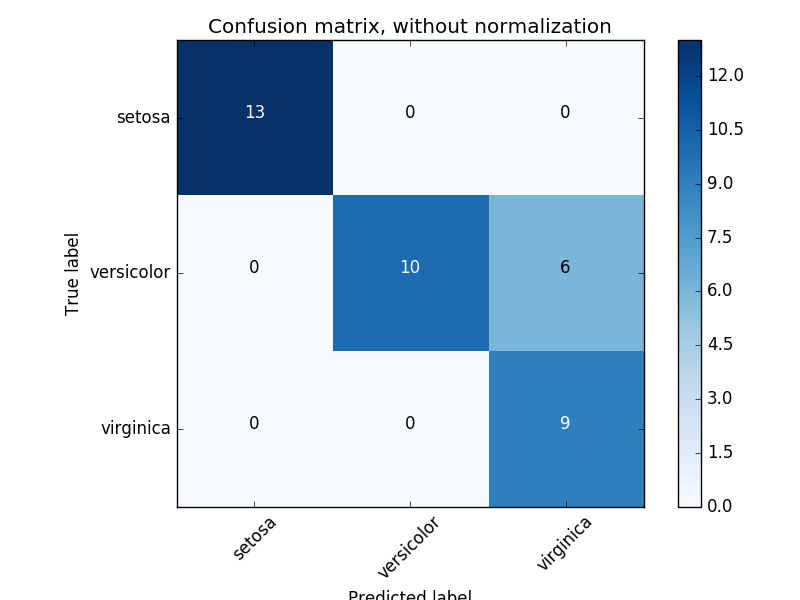
Pour les problèmes binaires, vous pouvez obtenir des nombres vrais négatifs, faux positifs, faux négatifs et vrais positifs comme suit:
--Exemple:
- Pour un exemple d'utilisation d'une matrice de confusion pour évaluer la qualité de sortie d'un classificateur, voir "[Matrice de confusion](http://scikit-learn.org/0.18/auto_examples/model_selection/plot_confusion_matrix.html#sphx-glr-auto". -examples-model-selection-plot-confusion-matrix-py) ".
- Pour un exemple d'utilisation d'une matrice de confusion pour classer des nombres manuscrits, voir Reconnaissance des nombres manuscrits (http://scikit-learn.org/0.18/auto_examples/classification/plot_digits_classification.html#sphx-glr-auto- Voir exemples-classification-plot-digits-classification-py).
- Pour un exemple de classification de documents texte à l'aide d'une matrice de confusion, voir Classifier des documents texte à l'aide de fonctions fragmentées (http://scikit-learn.org/0.18/auto_examples/text/document_classification_20newsgroups.html#sphx- glr-auto-exemples-texte-classification-de-documents-20newsgroups-py).
3.3.2.5. Rapport de classification
La fonction classification_report crée un rapport texte affichant les principales métriques de classification. Ce qui suit est un petit exemple d'un target_names personnalisé et d'une étiquette estimée.
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
avg / total 0.67 0.60 0.59 5
--Exemple:
- Pour un exemple d'utilisation du rapport de classification des numéros manuscrits, voir Reconnaissance des nombres manuscrits (http://scikit-learn.org/0.18/auto_examples/classification/plot_digits_classification.html#sphx-glr-auto-examples-classification-plot Voir -digits-classification-py). --Pour un exemple d'utilisation d'un rapport de classification de document texte, voir [Classifier des documents texte à l'aide de fonctions éparses](http://scikit-learn.org/0.18/auto_examples/text/document_classification_20newsgroups.html#sphx-glr-auto- Voir exemples-texte-document-classification-20newsgroups-py).
- Pour un exemple d'utilisation d'un rapport de classification de recherche de grille avec validation mutuelle imbriquée, voir Estimation des paramètres à l'aide de la recherche de grille avec validation mutuelle (http://scikit-learn.org/0.18/auto_examples/model_selection/grid_search_digits.html). Voir # sphx-glr-auto-examples-model-selection-grid-search-digits-py).
3.3.2.6. Perte de bourdonnement
hamming_loss calcule la perte moyenne de bourdonnement ou la distance de bourdonnement entre deux ensembles d'échantillons Faire. Si $ \ hat {y} j $ est la valeur prédite du $ j $ th label de l'échantillon donné, alors $ y_j $ est la valeur vraie correspondante et $ n \ text {labels} $ est la classe ou Le nombre d'étiquettes, la perte de bourdonnement $ L_ {Hamming} $, est défini comme suit.
L_{Hamming}(y, \hat{y}) = \frac{1}{n_\text{labels}} \sum_{j=0}^{n_\text{labels} - 1} 1(\hat{y}_j \not= y_j)
Où $ 1 (x) $ est la fonction d'indicateur (https://en.wikipedia.org/wiki/Indicator_function).
>>> from sklearn.metrics import hamming_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> hamming_loss(y_true, y_pred)
0.25
Pour multi-étiquettes avec indicateur d'étiquette binaire:
>>>
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2)))
0.75
** (Remarque) ** Dans la classification multi-classes, la perte de bourdonnement est [Zero One Loss](# 33213-% E3% 82% BC% E3% 83% AD1% E3% 81% A4% E3% 81% AE% E6 % 90% 8D% E5% A4% B1) Correspond à la distance de bourdonnement entre «y_true» et «y_pred», qui est similaire à la fonction. Cependant, les pertes en un contre un pénalisent les ensembles prédictifs qui ne correspondent pas exactement à l'ensemble réel, tandis que les pertes en bourdonnement pénalisent les étiquettes individuelles. Par conséquent, la perte de bourdonnement plafonnée par la perte de zéro 1 est toujours comprise entre 0 et 1, et prédire le sous-ensemble ou le sur-ensemble approprié du véritable label est un bourdonnement entre zéro et 1. La perte sera éliminée.
3.3.2.7. Score du coefficient de similarité Jacquard
jaccard_similarity_score La fonction est également appelée index Jaccard entre des ensembles d'étiquettes appariés] Calculez la moyenne (par défaut) ou le total des facteurs de genre (https://en.wikipedia.org/wiki/Jaccard_index). Le coefficient de similarité Jaccard pour le $ i $ ème échantillon avec le jeu d'étiquettes de valeur mesurée $ y_i $ et le jeu d'étiquettes prédites $ \ hat {y} _i $ est défini comme suit:
J(y_i, \hat{y}_i) = \frac{|y_i \cap \hat{y}_i|}{|y_i \cup \hat{y}_i|}.
Pour la classification binaire et multiclasse, le score du coefficient de similarité Jaccard est égal à la précision de la classification.
>>> import numpy as np
>>> from sklearn.metrics import jaccard_similarity_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> jaccard_similarity_score(y_true, y_pred)
0.5
>>> jaccard_similarity_score(y_true, y_pred, normalize=False)
2
Pour multi-étiquettes avec indicateur d'étiquette binaire:
>>>
>>> jaccard_similarity_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.75
3.3.2.8. Taux de conformité, taux de rappel, valeur F (mesure F)
Intuitivement, Fitility est la capacité du classificateur à empêcher les échantillons négatifs d'être étiquetés comme positifs. Rate](https://en.wikipedia.org/wiki/Precision_and_recall#Recall) est la capacité du classificateur à trouver tous les échantillons positifs. Les valeurs F (mesures $ F_β $ et $ F \ 1 $) peuvent être interprétées comme des moyennes harmonisées pondérées de précision et de rappel. Si $ \ beta = 1 $, $ F \ beta $ et $ F \ _1 $ sont équivalents, et le rappel et la précision sont tout aussi importants. precision_recall_curve est la courbe de taux de rappel de précision de l'étiquette de vérité. Calculez le score donné par le classifieur en modifiant le seuil. average_precision_score La fonction calcule la précision moyenne (AP) à partir du score prévu. .. Ce score correspond à la zone sous la courbe du taux de précision-rappel. La valeur est comprise entre 0 et 1, la plus élevée est la meilleure. Dans la prédiction aléatoire, AP est le pourcentage d'échantillons positifs.
Plusieurs fonctionnalités peuvent être utilisées pour analyser les scores de précision, de rappel et de valeur F.
| average_precision_score(y_true,y_score [,...]) | Taux de précision moyen à partir du score prévu(AP)Calculer |
| f1_score(y_true,y_pred [,labels,...]) | Calculez le score F1. Ceci est également appelé un score F équilibré ou F majeur |
| fbeta_score(y_true,y_pred,beta [,labels,...]) | Calculer le score F Beta |
| precision_recall_curve(y_true,probas_pred) | Taux d'adaptation à divers seuils de probabilité-Calculer les paires de rappel |
| precision_recall_fscore_support(y_true,y_pred) | Taux de conformité de chaque classe,Rappel,F-Calculer la mesure et le support |
| precision_score(y_true,y_pred [,labels,...]) | Calculez la précision |
| recall_score(y_true,y_pred [,labels,...]) | Calculer le rappel |
precision_recall_curve Notez que la fonction est limitée au binaire. .. La fonction average_precision_score ne fonctionne qu'en classification binaire et au format d'indicateur multi-étiquettes.
--Exemple: --Pour un exemple d'utilisation de f1_score pour classer des documents texte, cliquez sur Fonction Sparse Classer les documents texte utilisés S'il te plait donne moi.
- [Precision_score](http://scikit-learn.org/0.18/modules/generated/sklearn.metrics.precision_score.html#sklearn.metrics] pour estimer les paramètres à l'aide de la recherche de grille dans la validation mutuelle imbriquée Pour des exemples d'utilisation de .precision_score) et rappel_score, consultez Grid Search by Cross Validation. Estimation des paramètres à l'aide de [http://scikit-learn.org/0.18/auto_examples/model_selection/grid_search_digits.html#sphx-glr-auto-examples-model-selection-grid-search-digits-py) S'il vous plaît. --Pour un exemple d'utilisation de precision_recall_curve pour évaluer la qualité de sortie du classificateur Voir, Precision-Recall S'il vous plaît. --Pour un exemple d'utilisation de precision_recall_curve pour sélectionner des entités dans un modèle linéaire clairsemé , [Récupération parcimonieuse de modèles linéaires clairsemés: sélection de fonctionnalités](http://scikit-learn.org/0.18/auto_examples/linear_model/plot_sparse_recovery.html#sphx-glr-auto-examples-linear-model-plot-sparse-recovery Voir -py).
| average_precision_score(y_true,y_score [,...]) | Précision moyenne à partir du score prévu(AP)Calculer |
| f1_score(y_true,y_pred [,labels,...]) | Calculez le score F1. Ceci est également appelé un score F équilibré ou F majeur |
| fbeta_score(y_true,y_pred,beta [,labels,...]) | Calculer le score F Beta |
| precision_recall_curve(y_true,probas_pred) | Taux d'adaptation par rapport à des seuils de probabilités diverses-Calculer les paires de rappel |
| precision_recall_fscore_support(y_true,y_pred) | Taux de conformité de chaque classe,Rappel,Calculer la valeur F et le support |
| precision_score(y_true,y_pred [,labels,...]) | Calculez la précision |
| recall_score(y_true,y_pred [,labels,...]) | Calculer le rappel |
| precision_recall_Notez que la fonction de courbe est limitée au cas binaire. | average_precision_fonction de score,Ne fonctionne qu'en classification binaire et au format d'indicateur multi-étiquettes. |
Notez que la fonction precision_recall_curve est limitée aux cas binaires. La fonction average_precision_score fonctionne uniquement dans le format de classification binaire et d'indicateur multi-étiquettes. Exemple: Pour obtenir un exemple d'utilisation de f1_score pour classer des documents texte, voir Classifier des documents texte à l'aide de fonctions fragmentées. Pour obtenir un exemple d'utilisation de precision_score et rappel_score pour estimer des paramètres à l'aide de la recherche de grille dans la validation mutuelle imbriquée, consultez Estimation de paramètre à l'aide de la recherche de grille avec validation croisée. Voir Precision-Recall pour un exemple d'utilisation de precision_recall_curve pour évaluer la qualité de sortie d'un classificateur. Pour obtenir un exemple d'utilisation de precision_recall_curve pour sélectionner des entités dans un modèle linéaire clairsemé, voir Récupération clairsemée pour les modèles linéaires clairsemés: sélection d'entités.
3.3.2.8.1. Classification binaire
Dans la tâche de classification binaire, les termes «positif» et «négatif» font référence aux prédictions du classifieur, et les termes «vrai» et «faux» indiquent «observation» si les prédictions correspondent à des jugements externes. Aussi appelé). Compte tenu de ces définitions, vous pouvez créer le tableau suivant.
| Classe réelle (observation) | ||
|---|---|---|
| Classe de prédiction (valeur attendue) | tp (vrai positif) résultat correct | fp (faux positif) Résultat inattendu |
| résultat manquant fn (faux négatif) | Le résultat tn (vrai négatif) est incorrect |
Dans ce contexte, vous pouvez définir les concepts de précision, de rappel et de valeur F.
\text{precision} = \frac{tp}{tp + fp}, \\
\text{recall} = \frac{tp}{tp + fn}, \\
F_\beta = (1 + \beta^2) \frac{\text{precision} \times \text{recall}}{\beta^2 \text{precision} + \text{recall}}.
Voici quelques petits exemples de classification binaire:
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=0.5)
0.83...
>>> metrics.fbeta_score(y_true, y_pred, beta=1)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=2)
0.55...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5)
(array([ 0.66..., 1. ]), array([ 1. , 0.5]), array([ 0.71..., 0.83...]), array([2, 2]...))
>>> import numpy as np
>>> from sklearn.metrics import precision_recall_curve
>>> from sklearn.metrics import average_precision_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> precision, recall, threshold = precision_recall_curve(y_true, y_scores)
>>> precision
array([ 0.66..., 0.5 , 1. , 1. ])
>>> recall
array([ 1. , 0.5, 0.5, 0. ])
>>> threshold
array([ 0.35, 0.4 , 0.8 ])
>>> average_precision_score(y_true, y_scores)
0.79...
3.3.2.8.2. Classification des multi-classes et multi-étiquettes
Les tâches de classification multi-classes et multi-étiquettes vous permettent d'appliquer les concepts de précision, de rappel et de valeur F à chaque étiquette individuellement. Comme ci-dessus average_precision_score (multilabel uniquement), [f1_score](http: / /scikit-learn.org/0.18/modules/generated/sklearn.metrics.f1_score.html#sklearn.metrics.f1_score), [fbeta_score](http://scikit-learn.org/0.18/modules/generated/sklearn. metrics.fbeta_score.html # sklearn.metrics.fbeta_score), [precision_recall_fscore_support](http://scikit-learn.org/0.18/modules/generated/sklearn.metrics.precision_recall_fscore_support.html#sklearn_support.html#sklearn_fscore_support.html#sklearn. ](Http://scikit-learn.org/0.18/modules/generated/sklearn.metrics.precision_score.html#sklearn.metrics.precision_score) et [rappel_score](http://scikit-learn.org/0.18/ modules / generated / sklearn.metrics.recall_score.html # sklearn.metrics.recall_score) Il existe plusieurs façons de combiner les résultats entre les étiquettes spécifiées par l'argument ʻaverage` de la fonction. Une moyenne «micro» dans un cadre multi-classes qui inclut toutes les étiquettes produit des valeurs d'ajustement, de rappel et de F égales, mais une moyenne «pondérée» n'est pas entre l'ajustement et le rappel. Notez qu'un score F est généré.
Pour rendre cela plus explicite, considérez la notation suivante:
- $ y $ est l'ensemble des paires $ (échantillon, étiquette) $ prédites
- $ \ hat {y} $ est un ensemble de $ true (échantillon, étiquette) $ paires
- $ L $ est un ensemble d'étiquettes
- $ S $ est un ensemble d'échantillons
- $ y_s $ est un sous-ensemble de y, c'est-à-dire $ y_s: = \ left \\ {(s ', l) \ in y | s' = s \ right \} $
- $ y_l $ est un sous-ensemble de $ y $ avec l'étiquette $ l $
- De même, $ \ hat {y} \ _s $ et $ \ hat {y} \ _l $ sont des sous-ensembles de $ \ hat {y} $
P(A, B) := \frac{\left| A \cap B \right|}{\left|A\right|} R(A, B) := \frac{\left| A \cap B \right|}{\left|B\right|} (La règle de notation estB = \emptyset Cela dépend de la manipulation de. Cette implémentationR(A, B):=0 En utilisant,P Est le même).
F_\beta(A, B) := \left(1 + \beta^2\right) \frac{P(A, B) \times R(A, B)}{\beta^2 P(A, B) + R(A, B)}
Ensuite, la métrique est définie comme:
| average | Precision | Recall | F_beta |
|---|---|---|---|
"micro" | $P(y, \hat{y})$ | $R(y, \hat{y})$ | $F_\beta(y, \hat{y})$ |
"samples" |
$\frac{1}{\left|S\right|} \sum_{s \in S} P(y_s, \hat{y}_s)$ | $\frac{1}{\left|S\right|} \sum_{s \in S} R(y_s, \hat{y}_s)$ | $\frac{1}{\left|S\right|} \sum_{s \in S} F_\beta(y_s, \hat{y}_s)$ |
"macro" |
$\frac{1}{\left|L\right|} \sum_{l \in L} P(y_l, \hat{y}_l)$ | $\frac{1}{\left|L\right|} \sum_{l \in L} R(y_l, \hat{y}_l)$ | $\frac{1}{\left|L\right|} \sum_{l \in L} F_\beta(y_l, \hat{y}_l)$ |
"weighted" |
$\frac{1}{\sum_{l \in L} \left|\hat{y}_l\right|} \sum_{l \in L} \left|\hat{y}_l\right| P(y_l, \hat{y}_l)$ | $\frac{1}{\sum_{l \in L} \left|\hat{y}_l\right|} \sum_{l \in L} \left|\hat{y}_l\right| R(y_l, \hat{y}_l)$ | $\frac{1}{\sum_{l \in L} \left|\hat{y}_l\right|} \sum_{l \in L} \left|\hat{y}_l\right| F_\beta(y_l, \hat{y}_l)$ |
None |
$\langle P(y_l, \hat{y}_l) | l \in L \rangle$ | $\langle R(y_l, \hat{y}_l) | l \in L \rangle$ | $\langle F_\beta(y_l, \hat{y}_l) | l \in L \rangle$ |
>>> from sklearn import metrics
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> metrics.precision_score(y_true, y_pred, average='macro')
0.22...
>>> metrics.recall_score(y_true, y_pred, average='micro')
...
0.33...
>>> metrics.f1_score(y_true, y_pred, average='weighted')
0.26...
>>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5)
0.23...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None)
...
(array([ 0.66..., 0. , 0. ]), array([ 1., 0., 0.]), array([ 0.71..., 0. , 0. ]), array([2, 2, 2]...))
Certaines étiquettes peuvent être exclues des classifications multiclasses qui incluent des «classes négatives».
>>>
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro')
... # excluding 0, no labels were correctly recalled
0.0
De même, les étiquettes qui ne sont pas présentes dans l'échantillon de données peuvent être expliquées dans le calcul de la moyenne des macros.
>>>
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro')
...
0.166...
3.3.2.9. Perte de charnière
hinge_loss La fonction est une métrique unilatérale qui ne tient compte que des erreurs de prédiction [perte charnière] ](Https://en.wikipedia.org/wiki/Hinge_loss) est utilisé pour calculer la distance moyenne entre le modèle et les données. (La perte de charnière est utilisée dans les classificateurs de marge maximale tels que les machines vectorielles de support).
Si l'étiquette est codée avec +1 et -1, $ y: $ est la valeur vraie, $ w $ est la décision prédite comme sortie de decision_function, et la perte de charnière est la suivante: Il est défini.
L_\text{Hinge}(y, w) = \max\left\{1 - wy, 0\right\} = \left|1 - wy\right|_+
S'il y a plus d'une étiquette, hinte_loss utilise une variante multi-classes pour Crammer & Singer. Voici un article qui le décrit. Multiclasse si $ y_w $ est la décision prédite de la vraie étiquette et $ y_t $ est la décision maximale prévue de toutes les autres étiquettes pour lesquelles la décision prédite par la fonction de décision est sortie. Perte de charnière
L_\text{Hinge}(y_w, y_t) = \max\left\{1 + y_t - y_w, 0\right\}
Voici un petit exemple montrant comment utiliser la fonction hidden_loss avec le classificateur svm pour les problèmes de classe binaire.
>>> from sklearn import svm
>>> from sklearn.metrics import hinge_loss
>>> X = [[0], [1]]
>>> y = [-1, 1]
>>> est = svm.LinearSVC(random_state=0)
>>> est.fit(X, y)
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=0, tol=0.0001,
verbose=0)
>>> pred_decision = est.decision_function([[-2], [3], [0.5]])
>>> pred_decision
array([-2.18..., 2.36..., 0.09...])
>>> hinge_loss([-1, 1, 1], pred_decision)
0.3...
Voici un exemple d'utilisation de la fonction hige_loss avec le classificateur svm pour les problèmes multiclasses:
>>>
>>> X = np.array([[0], [1], [2], [3]])
>>> Y = np.array([0, 1, 2, 3])
>>> labels = np.array([0, 1, 2, 3])
>>> est = svm.LinearSVC()
>>> est.fit(X, Y)
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
verbose=0)
>>> pred_decision = est.decision_function([[-1], [2], [3]])
>>> y_true = [0, 2, 3]
>>> hinge_loss(y_true, pred_decision, labels)
0.56...
3.3.2.10. Perte de journal
La perte logarithmique, également appelée perte de régression logistique ou perte d'entropie croisée, est définie par l'estimation de probabilité. Il est couramment utilisé dans la régression logistique (polypoly) et les réseaux de neurones ainsi que dans certaines variantes de maximisation prédictive, et est utilisé pour évaluer la sortie probabiliste du classifieur (prédire_proba) au lieu de la prédiction discrète. peut faire.
Pour les classifications binaires avec le vrai libellé $ y \ in \ {0,1 } $ et l'estimation de probabilité $ p = \ operatorname {Pr} (y = 1) $, la perte de journal par échantillon est le vrai libellé Probabilité logarithmique négative d'un classificateur donné.
L_{\log}(y, p) = -\log \operatorname{Pr}(y|p) = -(y \log (p) + (1 - y) \log (1 - p))
Cela s'étend au cas des multi-classes comme suit. Encodez la vraie étiquette de l'ensemble d'échantillons comme l'une des K matrice d'indicateurs binaires $ Y $. Autrement dit, si l'échantillon i a une étiquette k tirée d'un ensemble de K étiquettes, alors $ y_ {i, k} = 1 $. Soit $ P $ la matrice d'estimation probabiliste et $ p_ {i, k} = \ operatorname {Pr} (t_ {i, k} = 1) $. Ensuite, la perte logarithmique de l'ensemble entier est
L_{\log}(Y, P) = -\log \operatorname{Pr}(Y|P) = - \frac{1}{N} \sum_{i=0}^{N-1} \sum_{k=0}^{K-1} y_{i,k} \log p_{i,k}
Si c'est binaire, $ p_ {i, 0} = 1 --p_ {i, 1} $ et $ y_ {i, 0} = 1 --y_ {i, 1} $ Par conséquent, le total interne est $ y_ {i, Supérieur à k} \ in \ {0,1 } $ entraînera une perte de journal binaire.
log_loss La fonction est maintenant renvoyée par la méthode d'estimation predire_proba. Calcule la perte logarithmique à partir d'une étiquette de vérité terrain et d'une liste de matrices de probabilité.
>>> from sklearn.metrics import log_loss
>>> y_true = [0, 0, 1, 1]
>>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
>>> log_loss(y_true, y_pred)
0.1738...
Le premier «[.9, .1]» de «y_pred» indique que le premier échantillon a 90% de chances d'avoir l'étiquette 0. La perte de journal n'est pas négative.
3.3.2.11. Coefficient de corrélation de Matthews
matthews_corrcoef La fonction est une classe binaire [Matthew Correlation Coefficient (MCC)]( (https://en.wikipedia.org/wiki/Matthews_correlation_coefficient) est calculé. Citer Wikipedia:
Les coefficients de corrélation de Matthews sont utilisés dans l'apprentissage automatique comme une mesure de la qualité de la classification binaire (2 classes). Compte tenu des vrais positifs et négatifs, positifs et négatifs, il est généralement considéré comme une mesure équilibrée qui peut être utilisée même dans des classes de tailles très différentes. MCC est essentiellement une valeur de coefficient de corrélation entre -1 et +1. Un coefficient de +1 représente une prédiction complète, 0 représente une prédiction aléatoire moyenne et -1 représente une prédiction inverse. Les statistiques sont également connues sous le nom de coefficient φ.
Si $ tp $, $ tn $, $ fp $ et $ fn $ sont respectivement des nombres vrais positifs, vrais négatifs, faux positifs et faux négatifs, le coefficient MCC est
MCC = \frac{tp \times tn - fp \times fn}{\sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.
Voici un petit exemple montrant comment utiliser la fonction matthews_corrcoef.
>>>
>>> sklearn.Importer à partir de métriques Matthews_corrcoef
>>> y_true = [+1、+1、+1、-1]
>>> y_pred = [+1、-1、+1、+1]
>>> matthews_corrcoef(y_true、y_pred)
-0.33 ...
3.3.2.12. Caractéristiques de fonctionnement du récepteur (ROC)
La fonction roc_curve est la [Recipient Behavior Characteristic Curve ou ROC Curve](https :: //en.wikipedia.org/wiki/Receiver_operating_characteristic) est calculé. Citer Wikipedia:
Les caractéristiques de fonctionnement du récepteur (ROC), ou simplement la courbe ROC, est un graphique montrant les performances du système de classification binaire lorsque le seuil discriminant change. Il est créé en traçant le pourcentage de vrais positifs à partir de positifs (TPR = taux de vrais positifs) par rapport au pourcentage de faux positifs à partir de négatifs (FPR = taux de faux positifs) à divers paramètres de seuil. La TPR est également connue sous le nom de susceptibilité, et la FPR est la spécificité ou le taux réel négatif moins un.
Cette fonction nécessite une vraie valeur binaire et un score cible. Il s'agit d'une estimation de probabilité de classe positive, d'une valeur de confiance ou d'une décision binaire. Voici un petit exemple d'utilisation de la fonction roc_curve.
>>> import numpy as np
>>> from sklearn.metrics import roc_curve
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)
>>> fpr
array([ 0. , 0.5, 0.5, 1. ])
>>> tpr
array([ 0.5, 0.5, 1. , 1. ])
>>> thresholds
array([ 0.8 , 0.4 , 0.35, 0.1 ])
Cette figure montre un exemple d'une telle courbe ROC.
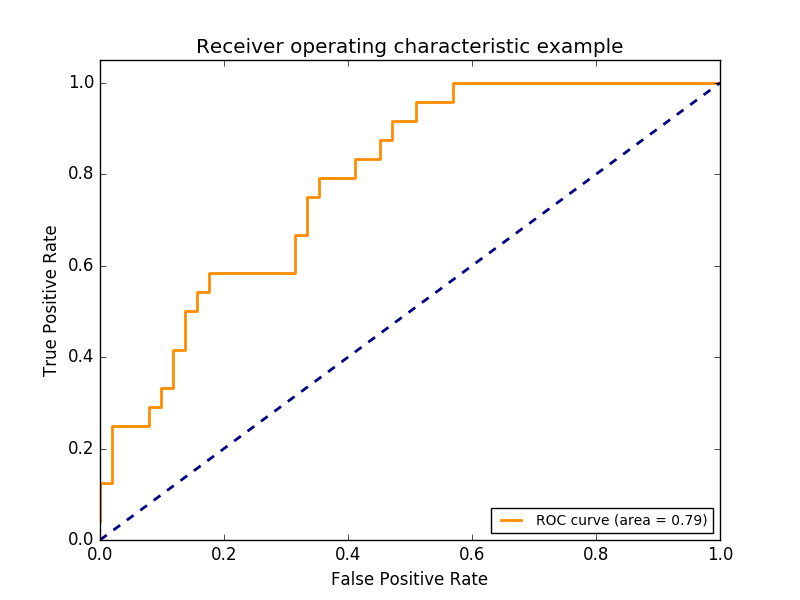
roc_auc_score La fonction est les caractéristiques de fonctionnement du récepteur (ROC) représentées par AUC ou AUROC. ) Calculez l'aire sous la courbe. En calculant l'aire sous la courbe roc, les informations de la courbe sont combinées en un seul nombre. Pour plus d'informations, consultez les articles de Wikipedia sur l'AUC (https://en.wikipedia.org/wiki/Receiver_operating_characteristic#Area_under_the_curve).
>>> import numpy as np
>>> from sklearn.metrics import roc_auc_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> roc_auc_score(y_true, y_scores)
0.75
Dans la classification multi-étiquettes, la fonction roc_auc_score est étendue en faisant la moyenne des étiquettes comme décrit ci-dessus. ROC ne nécessite pas l'optimisation du seuil pour chaque étiquette par rapport à des mesures telles que la précision du sous-ensemble, la perte de bourdonnement et le score F1. La fonction roc_auc_score peut également être utilisée dans la classification multiclasse si la sortie prédite a été évoluée en binaire.
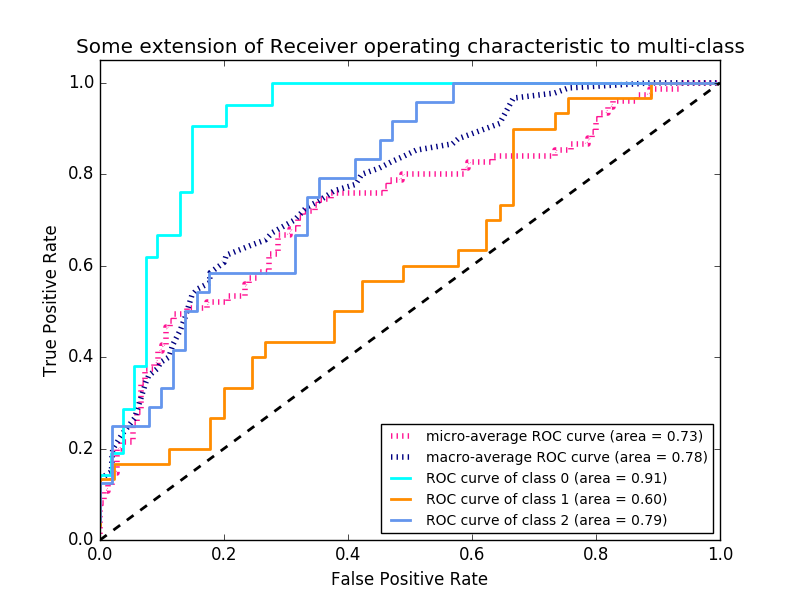
--Exemple:
- Pour un exemple d'utilisation de ROC pour évaluer la qualité de sortie d'un classificateur, voir Recipient Behavioral Characteristics (ROC) (http://scikit-learn.org/0.18/auto_examples/model_selection/plot_roc.html#sphx) Voir (-glr-auto-examples-model-selection-plot-roc-py). --Pour un exemple d'utilisation de ROC pour évaluer la qualité de sortie des classificateurs à l'aide de la validation croisée, voir [Recipient Behavior Characteristics by Mutual Verification (ROC)](http://scikit-learn.org/0.18/ Voir (auto_examples / model_selection / plot_roc_crossval.html # sphx-glr-auto-examples-model-selection-plot-roc-crossval-py). --Pour un exemple d'utilisation du ROC pour modéliser la distribution d'une espèce, voir Species Distribution Model (http://scikit-learn.org/0.18/auto_examples/applications/plot_species_distribution_modeling.html#sphx-glr-auto- Voir exemples-applications-parcelle-espèce-distribution-modélisation-py).
3.3.2.13. Perte 0-1
zero_one_loss La fonction est 0- pour $ n_ {\ text {samples}} $ 1 Calculez la somme ou la moyenne de la perte de classification $ (L_ {0-1}) $. Par défaut, la fonction est normalisée à l'échantillon. Pour trouver la somme de $ L_ {0-1} $, définissez normalize sur False.
Pour la classification multi-étiquettes, zero_one_loss attribue la valeur 1 au sous-ensemble si l'étiquette correspond exactement à la prédiction et la valeur zéro en cas d'erreur. Par défaut, cette fonction renvoie le pourcentage d'un sous-ensemble partiellement prédit. Pour obtenir le nombre de ces sous-ensembles à la place, définissez normalize sur False
Si $ \ hat {y} i $ est la valeur prédite pour le $ i $ e échantillon et $ y_i $ est la valeur vraie correspondante, alors la perte 0-1 $ L {0-1} $ est Est défini dans.
L_{0-1}(y_i, \hat{y}_i) = 1(\hat{y}_i \not= y_i)
Où $ 1 (x) $ est la fonction d'indicateur (https://en.wikipedia.org/wiki/Indicator_function).
>>> from sklearn.metrics import zero_one_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> zero_one_loss(y_true, y_pred)
0.25
>>> zero_one_loss(y_true, y_pred, normalize=False)
1
Pour les étiquettes multiples avec un indicateur d'étiquette binaire, il y a une erreur dans le premier jeu d'étiquettes [0,1].
>>>
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False)
1
--Exemple:
- Pour un exemple de perte de zéro pour la suppression de fonctionnalités récursives à l'aide de la validation croisée, voir Suppression de fonctionnalités récursives par validation croisée (http://scikit-learn.org/0.18/auto_examples) Voir /feature_selection/plot_rfe_with_cross_validation.html#sphx-glr-auto-examples-feature-selection-plot-rfe-with-cross-validation-py).
3.3.2.14. Perte du score de Brier
brier_score_loss La fonction est la classe binaire [Brier Score](https: // en) .wikipedia.org / wiki / Brier_score) est calculé. Citer Wikipedia:
Le score de Brier est une bonne fonction de notation qui mesure la précision des prédictions probabilistes. Applicable aux tâches où les prédictions doivent affecter des probabilités à un ensemble de résultats discrets mutuellement exclusifs.
Cette fonction renvoie le score de la différence quadratique moyenne entre le résultat réel et la probabilité attendue d'un résultat possible. Le résultat réel doit être 1 ou 0 (vrai ou faux), mais la probabilité prévue du résultat réel sera comprise entre 0 et 1. La perte de score de brier est également de 0 à 1, et plus le score est bas (plus la différence quadratique moyenne est petite), plus la prédiction est précise. Cela peut être considéré comme une mesure de la «mesure de distance» d'un ensemble de prédictions probabilistes.
BS = \frac{1}{N} \sum_{t=1}^{N}(f_t - o_t)^2
Où $ N $ est le nombre total de prédictions et $ f_t $ est la probabilité prédite du résultat réel $ o_t $.
Voici un petit exemple d'utilisation de cette fonction:
>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.4])
>>> y_pred = np.array([0, 1, 1, 0])
>>> brier_score_loss(y_true, y_prob)
0.055
>>> brier_score_loss(y_true, 1-y_prob, pos_label=0)
0.055
>>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham")
0.055
>>> brier_score_loss(y_true, y_prob > 0.5)
0.0
--Exemple:
- Pour un exemple d'utilisation de la perte de score de Brier pour effectuer des mesures de plage stochastique de classificateur, voir Mesures de plage probabiliste du classificateur (http://scikit-learn.org/0.18/auto_examples/calibration/plot_calibration. Voir html # sphx-glr-auto-examples-calibration-plot-calibration-py). --Référence: --G. Brier, Vérification des prévisions exprimées de manière probabiliste, Monthly Weather Assessment 78,1 (1950)
3.3.3. Métrique de classement multi-étiquettes
Avec l'apprentissage multi-étiquettes, chaque échantillon peut avoir n'importe quel nombre d'étiquettes vraies au sol qui lui sont associées. Le but est de donner un score élevé et de classer le prix de vérité sur le terrain.
3.3.3.1. Erreur de couverture
Coverage_error La fonction est définitive pour que toutes les vraies étiquettes soient prédites. Calculez le nombre moyen d'étiquettes à inclure dans une prévision typique. Ceci est utile si vous voulez savoir combien d'étiquettes de meilleur score vous devez prédire en moyenne sans perdre leur vraie valeur. Par conséquent, la meilleure valeur pour cette métrique est le nombre moyen d'étiquettes vraies. Officiellement, étant donné la matrice d'indicateurs binaires pour les étiquettes de vérité terrain et le score associé à chaque étiquette, la couverture est définie comme:
Officiellement, l'étiquette de vérité terrain $ y \ in \ left \\ {0, 1 \ right \} ^ {n \ _ \ text {samples} \ times n \ _ \ text {labels}} $ 2 Compte tenu de la matrice des indicateurs de base et du score associé à chaque étiquette $ \ hat {f} \ in \ mathbb {R} ^ {n \ _ \ text {samples} \ times n \ _ \ text {labels}} $ , Couverture
coverage(y, \hat{f}) = \frac{1}{n_{\text{samples}}}
\sum_{i=0}^{n_{\text{samples}} - 1} \max_{j:y_{ij} = 1} \text{rank}_{ij}
alorsy_scoresLes égalités sont rompues en donnant le rang maximum attribué à toutes les égalités.
Voici un petit exemple d'utilisation de cette fonction:
>>> import numpy as np
>>> from sklearn.metrics import coverage_error
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> coverage_error(y_true, y_score)
2.5
3.3.3.2. Taux de conformité moyen du rang d'étiquette
La fonction [label_ranking_average_precision_score](http://scikit-learn.org/0.18/modules/generated/sklearn.metrics.label_ranking_average_precision_score.html#sklearn.metrics.label_ranking_average_precision_score. Cette métrique est liée à la fonction average_precision_score, mais avec précision et rappel. Il est basé sur le concept de classement des étiquettes au lieu de. La précision moyenne du classement des étiquettes (LRAP) est la valeur moyenne de chaque étiquette Grand Truth attribuée à chaque échantillon et est le rapport entre les étiquettes vraies et le total des étiquettes avec un score faible. Cette métrique améliorera votre score si vous pouvez augmenter le rang de l'étiquette associée à chaque échantillon. Le score obtenu est toujours exactement supérieur à 0 et la meilleure valeur est 1. S'il existe exactement une étiquette associée par échantillon, le taux d'ajustement moyen du classement des étiquettes correspond au rang inverse moyen (https://en.wikipedia.org/wiki/Mean_reciprocal_rank). Formellement, la matrice d'index à deux éléments de la table de vérité terrain $ \ mathcal {R} ^ {n_ \ text {samples} \ times n_ \ text {labels}} $ et chaque étiquette $ \ hat {f} \ Dans mathcal {R} ^ {n_ \ text {samples} \ times n_ \ text {labels}} $, la précision moyenne est définie comme:
LRAP(y, \hat{f}) = \frac{1}{n_{\text{samples}}}
\sum_{i=0}^{n_{\text{samples}} - 1} \frac{1}{|y_i|}
\sum_{j:y_{ij} = 1} \frac{|\mathcal{L}_{ij}|}{\text{rank}_{ij}}
>>> import numpy as np
>>> from sklearn.metrics import label_ranking_average_precision_score
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_average_precision_score(y_true, y_score)
0.416...
3.3.3.3. Perte de classement
La fonction label_ranking_loss est le nombre de paires d'étiquettes mal ordonnées, ou de vraies étiquettes. Calcule une perte de classement qui fait la moyenne du nombre de paires d'étiquettes qui ont un score inférieur à la fausse étiquette et sont pondérées par l'inverse de la fausse étiquette et de la vraie étiquette. La perte de classement la plus basse possible est de zéro. La formule est 2 de l'étiquette de vérité terrain $ y \ in \ left \\ {0, 1 \ right \} \ ^ {n \ _ \ text {samples} \ times n \ _ \ text {labels}} $ Compte tenu de la matrice des indicateurs de base et du score associé à chaque étiquette $ \ hat {f} \ in \ mathbb {R} ^ {n \ _ \ text {samples} \ times n \ _ \ text {labels}} $ Si la perte de classement est
\text{ranking\_loss}(y, \hat{f}) = \frac{1}{n_{\text{samples}}}
\sum_{i=0}^{n_{\text{samples}} - 1} \frac{1}{|y_i|(n_\text{labels} - |y_i|)}
\left|\left\{(k, l): \hat{f}_{ik} < \hat{f}_{il}, y_{ik} = 1, y_{il} = 0 \right\}\right|
ici,$ |\cdot|
Un exemple d'utilisation de cette fonction est présenté ci-dessous.
>>> import numpy as np
>>> from sklearn.metrics import label_ranking_loss
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_loss(y_true, y_score)
0.75...
>>> # With the following prediction, we have perfect and minimal loss
>>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]])
>>> label_ranking_loss(y_true, y_score)
0.0
3.3.4. Métrique de régression
sklearn.metrics Les modules ont des pertes, des scores et des utilitaires pour mesurer les performances de régression. Implémente la fonction. mean_squared_error, [mean_absolute_error](http://scikit-learn.org/0.18.org /modules/generated/sklearn.metrics.mean_absolute_error.html#sklearn.metrics.mean_absolute_error), expliquer_variance_score, [Expliquer_variance_score](http://scikit-learn.org/0.18/modules/generated/sklearn.metricance_explained.variml. Gère plusieurs cas de sortie, tels que metrics.explained_variance_score) et r2_score Certains ont été étendus à.
Ces fonctions ont un argument de mot clé «multioutput» qui spécifie comment faire la moyenne des scores ou des pertes pour des cibles individuelles. La valeur par défaut est uniform_average ''. Ceci spécifie une moyenne uniformément pondérée pour la sortie. Si un `ndarray` avec une forme de` (n_outputs,) ʻest passé, l'entrée est interprétée comme un poids et une moyenne pondérée correspondante est renvoyée. Si `multioutput` vaut`'raw_values'`, tous les scores et pertes individuels qui n'ont pas changé sont renvoyés dans un tableau de formes` (n_outputs,) `. r2_score et describe_variance_score acceptent la valeur supplémentaire variance_weighted '' pour le paramètre multioutput. Cette option conduit à pondérer les scores individuels par la distribution des variables cibles correspondantes. Ce paramètre quantifie les variances non mises à l'échelle capturées globalement. Si les variables cibles sont à des échelles différentes, ce score est important pour mieux expliquer que les variables distribuées sont élevées. multioutput = 'variance_weighted' est la valeur par défaut de r2_score pour la compatibilité ascendante. Cela changera en `` uniform_average '' à l'avenir.
3.3.4.1. Score de la variable explicative
Expliquer_variance_score est [Score de régression des variables explicatives](https: //en.wikipedia) .org / wiki / Explained_variation) est calculé. Si $ \ hat {y} $ est la sortie cible estimée, $ y $ est la sortie cible correspondante (correcte) et $ Var $ est le carré de l'écart type, alors les variables explicatives sont: Est estimé comme.
\texttt{explained_variance}(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}}
Le score le plus élevé est de 1,0, plus la valeur est basse, pire c'est. Voici un exemple d'utilisation de la fonction describe_variance_score.
>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='raw_values')
...
array([ 0.967..., 1. ])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.990...
3.3.4.2. Erreur absolue moyenne
mean_absolute_error La fonction est [erreur absolue moyenne](https: //en.wikipedia) .org / wiki / Mean_absolute_error), calcule la métrique de risque correspondant à la valeur attendue de la perte d'erreur absolue ou de la perte de norme $ l1 $. Si $ \ hat {y} \ _i $ est la valeur prédite de l'échantillon $ i $ ème et $ y \ _i $ est la valeur vraie correspondante, alors $ n \ _ {\ text {samples}} $ L'erreur absolue moyenne estimée (MAE) est définie comme suit:
\text{MAE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \left| y_i - \hat{y}_i \right|.
Voici un exemple d'utilisation de la fonction mean_absolute_error.
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput='raw_values')
array([ 0.5, 1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.849...
3.3.4.3. Erreur quadratique moyenne
mean_squared_error La fonction est une perte d'erreur carrée (secondaire) ou une perte attendue Calculez la métrique de risque correspondante, l'erreur quadratique moyenne (https://en.wikipedia.org/wiki/Mean_squared_error). Si $ \ hat {y} \ _i $ est la valeur prédite de l'échantillon $ i $ ème et $ y \ _i $ est la valeur vraie correspondante, alors $ n \ _ {\ text {samples}} $ L'erreur quadratique moyenne estimée (MSE) est définie comme suit:
\text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2.
Voici un exemple d'utilisation de la fonction mean_squared_error.
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred)
0.7083...
--Exemple: --Pour un exemple d'utilisation de l'erreur moyenne au carré pour évaluer la régression d'amplification de gradient, voir Gradient Boost Regression (http://scikit-learn.org/0.18/auto_examples/ensemble/plot_gradient_boosting_regression.html#sphx-glr-auto) Voir -exemples-ensemble-plot-gradient-boosting-regression-py).
3.3.4.4. Erreur absolue centrale
median_absolute_error est particulièrement intéressant car il est robuste contre les valeurs aberrantes. Les pertes sont calculées en prenant la médiane de toutes les différences absolues entre la cible et la prévision. Si $ \ hat {y} \ _i $ est la valeur prédite de l'échantillon $ i $ ème et $ y \ _i $ est la valeur vraie correspondante, alors $ n \ _ {\ text {samples}} $ L'erreur absolue estimée en médiane (MedAE) est définie comme:
\text{MedAE}(y, \hat{y}) = \text{median}(\mid y_1 - \hat{y}_1 \mid, \ldots, \mid y_n - \hat{y}_n \mid).
median_absolute_error ne prend pas en charge la multi-sortie. Voici un exemple d'utilisation de la fonction median_absolute_error.
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
3.3.4.5. Score R², facteur de décision
r2_score La fonction est [Decision Factor](https: //en.wikipedia. org / wiki / Coefficient_of_determination) Calcule R². Cela fournit un indicateur que les futurs échantillons seront probablement prédits par le modèle. Le score le plus élevé possible est de 1,0 et peut être négatif (car le modèle peut se détériorer arbitrairement). Dans un modèle constant qui ignore les caractéristiques d'entrée et prédit toujours la valeur attendue de y, le score R ^ 2 est de 0,0. Si $ \ hat {y} \ _i $ est la valeur prédite de l'échantillon $ i $ e et $ y \ _i $ est la valeur vraie correspondante, alors $ n \ _ {\ text {samples}} $ Le score estimé R² est défini comme:
R^2(y, \hat{y}) = 1 - \frac{\sum_{i=0}^{n_{\text{samples}} - 1} (y_i - \hat{y}_i)^2}{\sum_{i=0}^{n_\text{samples} - 1} (y_i - \bar{y})^2}
$ \ bar {y} = \ frac {1} {n_ {\ text {samples}}} \ sum_ {i = 0} ^ {n_ {\ text {samples}} --1} y_i $. Voici un exemple d'utilisation de la fonction r2_score.
>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred)
0.948...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='variance_weighted')
...
0.938...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='uniform_average')
...
0.936...
>>> r2_score(y_true, y_pred, multioutput='raw_values')
...
array([ 0.965..., 0.908...])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
...
0.925...
--Exemple:
- Pour un exemple d'utilisation du score R² pour évaluer Lasso et Elastic Net avec des signaux clairsemés, voir Lasso et Elastic Net for Sparse Signals (http://scikit-learn.org/0.18/auto_examples/linear_model/plot_lasso_and_elasticnet) .html # sphx-glr-auto-examples-linear-model-plot-lasso-and-elasticnet-py).
3.3.5. Métrique de clustering
Le module sklearn.metrics implémente plusieurs fonctions de perte, de score et d'utilité. Pour plus d'informations, consultez la section Évaluation des performances du clustering (http://scikit-learn.org/0.18/modules/clustering.html#clustering-evaluation) de Instance Clustering and the Biclustering Evaluation of Biclustering (http: //: //). Voir scikit-learn.org/0.18/modules/biclustering.html#biclustering-evaluation).
3.3.6. Estimation fictive
Lors d'un apprentissage supervisé, un simple bilan de santé consiste à comparer l'estimateur à une règle empirique simple. DummyClassifier implémente certaines de ces stratégies simples de classification. Faire.
--stratified génère des prédictions aléatoires en respectant la distribution des classes de l'ensemble d'apprentissage.
--most_frequent prédit toujours les étiquettes les plus fréquentes dans l'ensemble d'apprentissage.
--prior prédit toujours la classe qui maximise la classe (comme la plus fréquente), et prédire_proba retourne la classe en premier.
--ʻUniform générera aléatoirement une prédiction uniforme. --constant` ** Renvoie toujours une étiquette de constante fournie par l'utilisateur en tant que prédiction. ** **
- La principale motivation de cette méthode est la notation F1 lorsque la classe positive est minoritaire.
Dans toutes ces stratégies, la méthode «prédire» ignore complètement les données d'entrée. Pour expliquer DummyClassifier, créons d'abord un jeu de données déséquilibré:
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> y[y != 1] = -1
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Ensuite, comparons la précision de «SVC» et de «most_frequent».
>>> from sklearn.dummy import DummyClassifier
>>> from sklearn.svm import SVC
>>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.63...
>>> clf = DummyClassifier(strategy='most_frequent',random_state=0)
>>> clf.fit(X_train, y_train)
DummyClassifier(constant=None, random_state=0, strategy='most_frequent')
>>> clf.score(X_test, y_test)
0.57...
Nous constatons que SVC n'est pas beaucoup mieux qu'un classificateur factice. Maintenant, changeons le noyau:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.97...
La précision s'est améliorée à presque 100%. Si le coût du processeur n'est pas très élevé, une validation croisée est recommandée pour une évaluation plus précise de la précision. Pour plus d'informations, consultez la section Validation croisée: évaluation des performances estimées (http://qiita.com/nazoking@github/items/13b167283590f512d99a). De plus, il est fortement recommandé d'utiliser la méthode appropriée lors de l'optimisation de l'espace des paramètres. Pour plus d'informations, reportez-vous à la section Réglage HyperParamètre Estimator (http://scikit-learn.org/0.18/modules/grid_search.html#grid-search). Plus généralement, si la précision du classifieur est trop proche de l'aléatoire, il se peut qu'il y ait un problème. Les fonctionnalités sont inutiles, les hyperparamètres ne sont pas ajustés correctement, les classificateurs souffrent de déséquilibres de classe, etc.
DummyRegressor implémente également quatre règles empiriques simples pour la régression. Je suis.
--mean prédit toujours la moyenne des objectifs d'entraînement.
- «median» prédit toujours la valeur médiane des objectifs d'entraînement.
--
quantileprédit toujours que l'utilisateur fournira un point de division pour l'objectif d'entraînement. --constantrenvoie toujours une valeur constante fournie par l'utilisateur en tant que prédiction.
Dans toutes ces stratégies, la méthode «prédire» ignore complètement les données d'entrée.
[scikit-learn 0.18 Guide de l'utilisateur 3. Sélection et évaluation du modèle](http://qiita.com/nazoking@github/items/267f2371757516f8c168#3-%E3%83%A2%E3%83%87%E3%83] À partir de% AB% E3% 81% AE% E9% 81% B8% E6% 8A% 9E% E3% 81% A8% E8% A9% 95% E4% BE% A1)
© 2010 --2016, développeurs scikit-learn (licence BSD).
Recommended Posts