[PYTHON] Comment utiliser x-means

Résumé du système k-means

--k-means: minimise l'erreur quadratique du centre de gravité du cluster. --k-medoids: Effectuez la procédure EM de sorte que la dissemblance totale des médoïdes du cluster (les points appartenant au cluster et la dissimilarité totale est la plus petite) soit minimisée. --x-means: contrôle la division du cluster basée sur BIC. --g-menas: contrôle la division du cluster par le test d'Anderson chéri, en supposant que les données sont basées sur une distribution normale. --gx-means: les deux extensions ci-dessus. --etc (Voir le readme de pyclustering. Il en existe plusieurs)

Déterminer le nombre de clusters

Ce serait bien si le nombre de grappes pouvait être connu immédiatement par les humains en regardant les données, mais c'est rare, alors j'aimerais une méthode de jugement quantitatif.

Selon feuille de triche sklearn

• MeanShift
• VBGMM

Est recommandé.

• Méthode du coude

C'est aussi utile, mais d'après mon expérience, il était rare pour moi d'obtenir un beau coude (un point où le graphique devient saccadé), et j'étais souvent confus sur le nombre de clusters.

Il existe une méthode x-means pour effectuer le clustering avec le nombre de clusters de manière entièrement automatique.

Ci-dessous, comment utiliser la bibliothèque "pyclustering" qui contient diverses méthodes de clustering, y compris x-means.

Comment utiliser le pyclustering

pyclustering est une bibliothèque d'algorithmes de clustering implémentés en python et C ++.

Installation

Paquets dépendants: scipy, matplotlib, numpy, PIL

pip install pyclustering

exemple d'utilisation de x-means

Code source

En plus de l'étape EM dans k-means, x-means détermine une nouvelle étape: si une grappe est représentée par deux ou une distribution normale, et les deux déterminent. Le cas échéant, l'opération consiste à diviser le cluster en deux.

Ci-dessous, le notebook jupyter est utilisé.

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt 
from sklearn import cluster, preprocessing
 
#Ensemble de données sur le vin
df_wine_all=pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
#Variété(Rangée 0, 1-3)Et la couleur (10 rangées) et la quantité de proline(13 rangées)Utiliser
df_wine=df_wine_all[[0,10,13]]
df_wine.columns = [u'class', u'color', u'proline']
 
#Mise en forme des données
X=df_wine[["color","proline"]]
sc=preprocessing.StandardScaler()
sc.fit(X)
X_norm=sc.transform(X)
 
#terrain
%matplotlib inline
 
x=X_norm[:,0]
y=X_norm[:,1]
z=df_wine["class"]
plt.figure(figsize=(10,10))
plt.subplot(4, 1, 1)
plt.scatter(x,y, c=z)
plt.show

# x-means
from pyclustering.cluster.xmeans import xmeans
from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer
xm_c = kmeans_plusplus_initializer(X_norm, 2).initialize()
xm_i = xmeans(data=X_norm, initial_centers=xm_c, kmax=20, ccore=True)
xm_i.process()

#Tracez les résultats
z_xm = np.ones(X_norm.shape[0])
for k in range(len(xm_i._xmeans__clusters)):
    z_xm[xm_i._xmeans__clusters[k]] = k+1

plt.subplot(4, 1, 2)
plt.scatter(x,y, c=z_xm)
centers = np.array(xm_i._xmeans__centers)
plt.scatter(centers[:,0],centers[:,1],s=250, marker='*',c='red')
plt.show

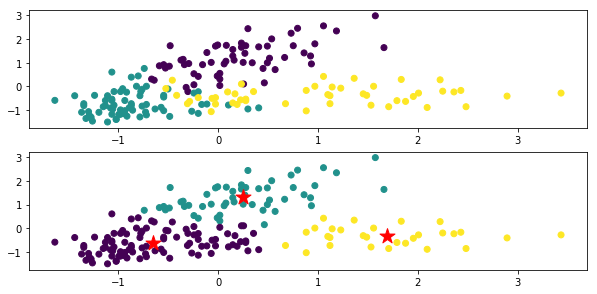
Le haut est le chiffre coloré pour chaque classe des données d'origine, et le bas est le résultat du regroupement par x-means. La marque ★ est le centre de gravité de chaque classe.

Dans le code xm_c = kmeans_plusplus_initializer (X_norm, 2) .initialize (), la valeur initiale du nombre de clusters est fixée à 2, mais elle se regroupe correctement sur 3.

J'utilise x-means avec xm_i.process ().

Pour l'instance x-means (xm_i dans le code ci-dessus), si vous regardez les variables d'instance avant et après l'apprentissage, vous pouvez voir à quoi ressemble le résultat d'apprentissage. Par exemple

xm_i.__dict__.keys()

Ou

vars(xm_i).keys()

Peut être obtenu avec

dict_keys(['_xmeans__pointer_data', '_xmeans__clusters', '_xmeans__centers', '_xmeans__kmax', '_xmeans__tolerance', '_xmeans__criterion', '_xmeans__ccore'])

Je pense que vous devriez examiner diverses choses telles que.

_xmeans__pointer_data

Une copie des données à regrouper.

_xmeans__clusters

Une liste indiquant quelle ligne des données d'origine (\ _xmeans__pointer_data) appartient à chaque cluster.

Le nombre d'éléments dans la liste est le même que le nombre de clusters, chaque élément est également une liste et le numéro de la ligne appartenant au cluster est stocké.

_xmeans__centers

Une liste de coordonnées centroïdes (listes) pour chaque cluster

_xmeans__kmax

Nombre maximum de clusters (valeur définie)

_xmeans__tolerance

Une constante qui détermine la condition d'arrêt pour l'itération x-means. L'algorithme se termine lorsque le changement maximal du centre de gravité de l'amas tombe en dessous de cette constante.

_xmeans__criterion

C'est une condition de jugement de la division de cluster. Par défaut: BIC

_xmeans__ccore

Il s'agit de la valeur de paramètre permettant d'utiliser ou non le code C ++ au lieu du code Python.