Exemple de configuration de problème

Exemple 1) Résolvez l'équation de Laplace. Comme le montre la figure, la condition aux limites est \ phi = V volt à y = 0. Il est mis à la terre à d'autres frontières et est de 0 volt. La position électrostatique à ce moment est déterminée et visualisée.

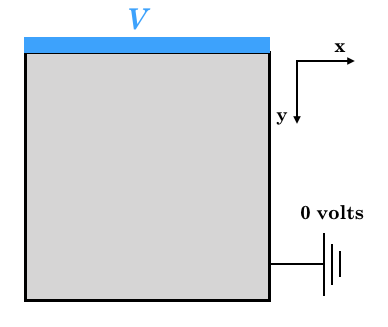
Exemple (2) Résolvez l'équation de Poisson. Mettez la charge externe Q dans la région considérée dans l'exemple (1). A ce moment, la position électrostatique $ \ phi $ et le champ électrique $ E = - \ nabla \ phi $ sont obtenus et visualisés.

Exemple (1) Équation de Poisson

L'animation est également générée dans le code. Il s'agit d'étudier comment la solution \ phi (x, y) converge.

Postscript 17 décembre 2017: il est supposé fonctionner sur jupyter. Si vous n'utilisez pas jupyter, commentez "% matplotlib nbagg" dans votre code. Du point de vue de masa_stone22.

laplace.py3

"""
Équation de Laplace:Solution numérique,Jacobi(Jacobi)Loi: 
12 Aug. 2017
"""
%matplotlib nbagg 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation #Importer des méthodes pour créer des animations

fig = plt.figure()
anim = [] 

# 
delta_L=0.1  #Largeur de la grille
LL = 10 #Largeur carrée
L = int(LL/delta_L)

V = 5.0 #Potentiel limite unilatéral
convegence_criterion = 10**-3  #Condition de convergence. Si vous souhaitez améliorer la précision, diminuez cette valeur.

phi = np.zeros([L+1,L+1])
phi[0,:] = V #condition limite
phi2 = np.empty ([L+1,L+1])

#for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])

    
#Principale
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
    if n_iter % 100 ==0:  #Suivi de l'état de la convergence
        print("iteration No =", n_iter, "delta=",delta)
    conv_check.append([n_iter, delta])
    for i in range(L+1):
        for j in range(L+1):
            if i ==0 or i ==L or j==0 or j==L:
                phi2[i,j] = phi[i,j]
            else: 
                phi2[i,j] = (phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4 #Addenda:formule(11)Voir
    delta = np.max(abs(phi-phi2))

    phi, phi2 = phi2, phi
    n_iter+=1
    
    im=plt.imshow(phi,cmap='hsv')
    anim.append([im])

#for plot        
plt.colorbar () #Affichage de la barre de couleur
plt.xlabel('X')
plt.ylabel('Y')
ani = ArtistAnimation(fig, anim, interval=100, blit=True,repeat_delay=1000)
ani.save("t.gif", writer='imagemagick')  
plt.show()

Résultat (1) Solution de l'équation de Laplace

La condition aux limites $ \ phi = 5 $ de y = 0 est satisfaite. Le changement de potentiel est important près de la frontière.

Exemple (2) Solution de l'équation de Poisson lorsqu'une charge externe est intégrée

La densité de charge externe était $ c = 1000 $, et le potentiel aux limites était $ V = 5 $.

Poisson.py3

"""
Équation de Poisson:Jacobi(Jacobi)Loi
Affiche également le champ électrique: 
12 Aug. 2017
"""
%matplotlib nbagg 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation #Importer des méthodes pour créer des animations

anim = [] 

# 
delta_L=0.01 #Largeur de la grille
LL = 1 #Largeur carrée
L = int(LL/delta_L)

V = 5.0 #Limite y=0 potentiel(condition limite)
convegence_criterion = 10**-5

phi = np.zeros([L+1,L+1])
phi[0,:] = V #condition limite
phi2 = np.empty ([L+1,L+1])

#Réglage de la densité de charge
eps0=1
charge= np.zeros([L+1,L+1])
c=1000 #Densité de charge

CC=int(L/4)
CC2=int(L/2)

#Densité de charge x=[L/4, L/2], y=[L/4,L/2]Incorporer dans la zone de
for i in range(CC, CC2+1):
    for j in range(CC,CC2+1):
        charge[i,j] = c
#

#for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])

    
#Principale
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
    if n_iter % 100 ==0:  #Suivi de l'état de la convergence
        print("iteration No =", n_iter, "delta=",delta)
    conv_check.append([n_iter, delta])
    for i in range(L+1):
        for j in range(L+1):
            if i ==0 or i ==L or j==0 or j==L:
                phi2[i,j] = phi[i,j]
            else: 
                phi2[i,j] = (phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4 + (delta_L**2/(4*eps0))*charge[i,j]
    delta = np.max(abs(phi-phi2))

    phi, phi2 = phi2, phi
    n_iter+=1
    
    im=plt.imshow(phi,cmap='hsv')
    anim.append([im])

    
#for plot    

pp=plt.colorbar (orientation="vertical") #Affichage de la barre de couleur
pp.set_label("phi", fontname="Ariel", fontsize=24)
plt.xlabel('X',fontname="Ariel", fontsize=24)
plt.ylabel('Y',fontname="Ariel", fontsize=24)
plt.title('Solution of the Poisson equation for electrostatic potential ')
#ani = ArtistAnimation(fig, anim, interval=10, blit=True,repeat_delay=1000)
#ani.save("t.gif", writer='imagemagick')  

plt.show()



#Calcul du champ électrique
Ex = np.zeros([L,L])
Ey = np.zeros([L,L])

for i in range(L):
    for j in range(L):
        Ex[i,j] = -(phi[i+1,j]-phi[i,j])/delta_L
        Ey[i,j] = -(phi[i,j+1]-phi[i,j])/delta_L

plt.figure()
        
X, Y= np.meshgrid(np.arange(0, L,1), np.arange(0, L,1))  #Génération de maillage
plt.quiver(X,Y,Ex,Ey,color='red',angles='xy',scale_units='xy', scale=40) #Champ vectoriel de tracé

plt.xlim([0,L]) #Plage de X à dessiner
plt.ylim([0,L]) #Plage de y pour dessiner

#Dessin graphique
plt.grid()
plt.draw()
plt.show()

Résultat (2): Solution de l'équation de Poisson pour un système avec charges externes intégrées

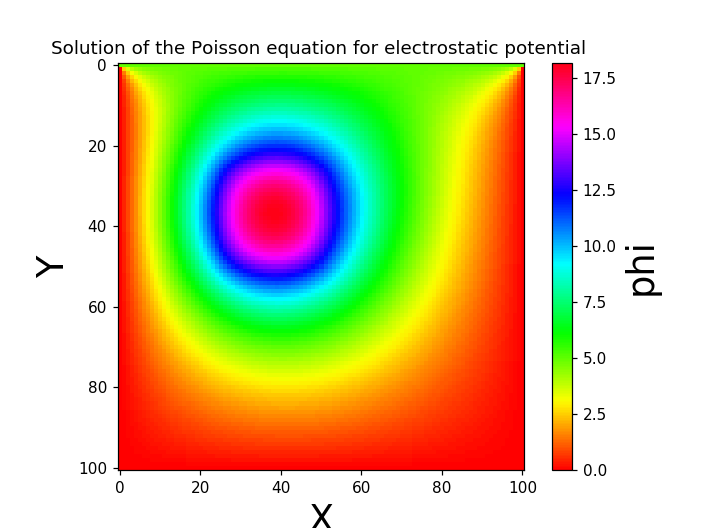
La condition aux limites en y = 0 est $ \ phi = 5 $. En raison de la charge externe intégrée, le potentiel diffère considérablement par rapport à l'exemple (1).

L'état du champ électrique. (L'axe #y a été inversé). Ce chiffre a été dessiné sous la forme delta_L = 0.1 ''`. Comme attendu de la fluctuation du potentiel, le champ électrique fluctue fortement près de la charge externe.

Addenda

Addendum (1): Théorie

L'expression relationnelle entre le champ électrostatique $ E $ et le potentiel $ \ phi $ E = - \nabla \phi \tag{1} Et la loi de Gauss entre les densités de charge $ \ rho $ et $ E $

\nabla \cdot E =\frac{\rho} {\epsilon_0} \tag{2}

Est le point de départ.

Remplacer (1) par (2)

\Delta \phi (x,y,z) =-\frac{\rho (x,y,z)} {\epsilon_0} \tag{3}

Obtenir. C'est l'équation de Poisson. Où $ \ epsilon_0 $ est la constante diélectrique dans le vide.

S'il n'y a pas de vraie charge partout dans l'espace ($ \ rho (x, y, z) = 0 $), l'équation de Poisson

\Delta \phi (x,y,z) =0 \tag{4} Sera. C'est l'équation de Laplace.

Addendum (2): Solution numérique: méthode Jacobi

Pensez à deux dimensions. Équation de Poisson

$ \frac{\partial^2 \phi(x,y)}{\partial x^2} + \frac{\partial^2 \phi(x,y)}{\partial y^2} =-\frac{\rho (x,y,z)} {\epsilon_0} \tag{5}$

Sera. Considérons une grille bidimensionnelle (voir figure ci-dessous) séparée par une largeur de $ \ Delta $ dans les directions $ x $ et $ y $. Lorsque le potentiel $ \ phi (x, y) $ est développé par Taylor au point ($ x + \ Delta, y $),

\phi(x+\Delta,y)=\phi(x,y)+\frac{\partial \phi}{\partial x}\Delta +\frac{1}{2}\frac{\partial^2 \phi}{\partial x^2}\Delta^2 + \frac{1}{6}\frac{\partial^3 \phi}{\partial x^3}\Delta^3+\frac{1}{24}\frac{\partial^4 \phi}{\partial x^4}\Delta^4 + \mathcal{O}(\Delta^5) \tag{6}

\phi(x-\Delta,y)=\phi(x,y)-\frac{\partial \phi}{\partial x}\Delta +\frac{1}{2}\frac{\partial^2 \phi}{\partial x^2}\Delta^2 - \frac{1}{6}\frac{\partial^3 \phi}{\partial x^3}\Delta^3+\frac{1}{24}\frac{\partial^4 \phi}{\partial x^4}\Delta^4 + \mathcal{O}(\Delta^5) \tag{7}

Lorsque les équations (6) et (7) sont additionnées,

$\frac{\partial^2 \phi(x,y)}{\partial x^2} = \frac{\phi(x+\Delta,y)+ \phi(x-\Delta,y)-2\phi(x,y)}{\Delta^2} +\mathcal{O}(\Delta^2) \tag{8} $

Faites l'expansion de Taylor pour y de la même manière, $\frac{\partial^2 \phi(x,y)}{\partial y^2} = \frac{\phi(x,y+\Delta)+ \phi(x,y-\Delta)-2\phi(x,y)}{\Delta^2} +\mathcal{O}(\Delta^2) \tag{9} $

Obtenir. Remplacez les équations (8) et (9) par (5) et triez-les un peu.

$ \phi(x,y) = \frac{1}{4} [\phi(x+\Delta,y)+\phi(x-\Delta,y)+\phi(x,y+\Delta)+\phi(x,y-\Delta)]+\frac{\rho(x,y)}{4 \epsilon_0}\Delta^2+\mathcal{O}(\Delta^4) \tag{10} $

Obtenir. Il s'agit d'une ** représentation différentielle de l'équation de Poisson **. L'erreur est $ \ mathcal {O} (\ Delta ^ 4) $.

Lorsque $ \ rho (x, y) = 0 $

$\phi(x,y) = \frac{1}{4} [\phi(x+\Delta,y)+\phi(x-\Delta,y)+\phi(x,y+\Delta)+\phi(x,y-\Delta)]+\mathcal{O}(\Delta^4) \tag{11} $

Sera. Il s'agit d'une ** représentation différentielle de l'équation de Laplace **.

Dans le calcul numérique, si l'indice du tableau est $ (x_i, y_j) $, l'équation (10) est

$ \phi(x_i,y_j) = \frac{1}{4} [\phi(x_{i+1},y_{j})+\phi(x_{i-1},y_{j})+\phi(x_{i},y_{j+1})+\phi(x_{i},y_{j-1})]+\frac{\rho(x_{i},y_{j})}{4\epsilon_0}\Delta^2　\tag{12} $ Sera.

Le potentiel $ \ phi (i, j) $ au point $ (x_i, y_j) $ est approximé en ajoutant le montant proportionnel à la densité de charge $ \ rho (x, y) $ à la valeur moyenne des valeurs des quatre points environnants. C'est fait (voir la figure ci-dessous).

** Tout d'abord, donnez la condition aux limites et la valeur estimée du potentiel dans la région, résolvez l'équation (12) dans toutes les régions et répétez jusqu'à ce que la solution dans la région converge. C'est la méthode Jacobi. ** Le nombre d'étapes répétées pour la convergence est approximativement proportionnel au carré du nombre de points de données [1].

Cette méthode est très lente à converger et peu pratique, mais elle fournit une base pour comprendre les méthodes modernes.

Les références

La méthode Jacobi et une bonne méthode de calcul légèrement modifiée [méthode Gauss-Seidel](https://ja.wikipedia.org/wiki/%E3%82%AC%E3%82%A6%E3%82% B9% EF% BC% 9D% E3% 82% B6% E3% 82% A4% E3% 83% 87% E3% 83% AB% E6% B3% 95) est lent à converger et peu pratique. Les schémas plus rapides incluent la méthode de sur-atténuation séquentielle (méthode SOR) (https://ja.wikipedia.org/wiki/SOR%E6%B3%95) [1,2].

[1] ["Recette numérique en version japonaise de la mer-Recette pour le calcul numérique en langage C"](https://www.amazon.co.jp/%E3%83%8B%E3%83%A5 % E3% 83% BC% E3% 83% A1% E3% 83% AA% E3% 82% AB% E3% 83% AB% E3% 83% AC% E3% 82% B7% E3% 83% 94-% E3% 82% A4% E3% 83% B3-% E3% 82% B7% E3% 83% BC-% E6% 97% A5% E6% 9C% AC% E8% AA% 9E% E7% 89% 88- C% E8% A8% 80% E8% AA% 9E% E3% 81% AB% E3% 82% 88% E3% 82% 8B% E6% 95% B0% E5% 80% A4% E8% A8% 88% E7% AE% 97% E3% 81% AE% E3% 83% AC% E3% 82% B7% E3% 83% 94-Press-William-H / dp / 4874085601 / ref = dp_return_1? _ Encoding = UTF8 & n = 465392 & s = livres) Revue technique, 1993.

Comme quelque chose qui peut être vu sur le net

http://www.na.scitec.kobe-u.ac.jp/~yamamoto/lectures/appliedmathematics2006/chapter8.PDF

Quand

http://web.econ.keio.ac.jp/staff/ito/pdf02/pde2.pdf

Je vais énumérer.

Postscript: 14 août 2017

J'ai posté un article sur la méthode SOR et la méthode Gauss Seidel.

[2] Article Qiita, [[Calcul scientifique / technique par Python] Comparaison des vitesses de convergence de la méthode Jacobi / Méthode Gauss-Seidel / Méthode SOR pour l'équation de Laplace, équation différentielle partielle, problème de valeur aux limites, calcul numérique](http: // qiita.com/sci_Haru/items/b98791f232b93690a6c3)

Addendum: ** Code pour résoudre l'équation de Poisson par la méthode SOR **

Le code pour résoudre l'équation de Poisson dans l'exemple (2) par la méthode SOR expliquée dans l'article [2] est posté. Elle converge plus de 10 fois plus vite que la méthode Jakobi </ font>, alors utilisez ceci.

"""
Équation de Poisson:Solution numérique,Méthode SOR
Affiche également le champ électrique:
14 Aug. 2017
"""
%matplotlib nbagg 
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation #Importer des méthodes pour créer des animations
import matplotlib.animation as animation


anim = [] 

# 
delta_Lx=0.01
delta_Ly=0.01
LLx = 1 #Largeur carrée
LLy= 1

Lx = int(LLx/delta_Lx)
Ly = int(LLy/delta_Ly)



V = 5.0 #Tension
convegence_criterion = 10**-5

phi = np.zeros([Lx+1,Ly+1])
phi_Bound= np.zeros([Lx+1,Ly+1])
phi_Bound[0,:] = V #condition limite

#Réglage de la densité de charge
eps0=1
charge= np.zeros([Lx+1,Ly+1])
c=1000

CC=int(Lx/4)
CC2=int(Ly/2)

for i in range(CC, CC2+1):
    for j in range(CC,CC2+1):
        charge[i,j] = c
#


# for SOR method
aa_recta=0.5*(np.cos(np.pi/Lx)+np.cos(np.pi/Ly))
omega_SOR_recta = 2/(1+np.sqrt(1-aa_recta**2)) #Paramètres d'accélération dans la méthode SOR
print("omega_SOR_rect=",omega_SOR_recta)



#for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])

    
#Principale
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
    phi_in=phi.copy()
    if n_iter % 100 ==0:  #Suivi de l'état de la convergence
        print("iteration No =", n_iter, "delta=",delta)
    conv_check.append([n_iter, delta])
    for i in range(Lx+1):
        for j in range(Ly+1):
            if i ==0 or i ==Lx or j==0 or j==Ly:
                phi[i,j] = phi_Bound[i,j]
            else: 
                phi[i,j] = phi[i,j]+omega_SOR_recta *((phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4-phi[i,j]+ (delta_Lx*delta_Ly/(4*eps0))*charge[i,j]) # SOR =Gauss-Seidel+ OR
    delta = np.max(abs(phi-phi_in))


    n_iter+=1
    
    im=plt.imshow(phi,cmap='hsv')
    anim.append([im])

    
#for plot    

pp=plt.colorbar (orientation="vertical") #Affichage de la barre de couleur
pp.set_label("phi", fontname="Ariel", fontsize=24)
plt.xlabel('X',fontname="Ariel", fontsize=24)
plt.ylabel('Y',fontname="Ariel",  fontsize=24)
plt.title('Solution of the Poisson equation for electrostatic potential ')
#ani = ArtistAnimation(fig, anim, interval=10, blit=True,repeat_delay=1000)
#ani.save("t.gif", writer='imagemagick')  

plt.show()



#Calcul du champ électrique
Ex = np.zeros([Lx,Ly])
Ey = np.zeros([Lx,Ly])

for i in range(Lx):
    for j in range(Ly):
        Ex[i,j] = -(phi[i+1,j]-phi[i,j])/delta_Lx
        Ey[i,j] = -(phi[i,j+1]-phi[i,j])/delta_Ly

plt.figure()

X, Y= np.meshgrid(np.arange(0, Lx,1), np.arange(0, Ly,1))  #Génération de maillage
plt.quiver(X,Y,Ex,Ey,color='red',angles='xy',scale_units='xy', scale=40) #Champ vectoriel de tracé

plt.xlim([0,Lx]) #Plage de X à dessiner
plt.ylim([0,Ly]) #Plage de y pour dessiner

#Dessin graphique
plt.grid()
plt.draw()
plt.show()