[PYTHON] [Maschinelles Lernen] Was ist LP-Norm?

Beim Studium des maschinellen Lernens kommen meiner Meinung nach die Begriffe L1-Regularisierung und L2-Regularisierung vor. [^ 1]

[^ 1]: TJOs "Blog der in Ginza arbeitenden Datenwissenschaftler" L1 / L2-Regularisierung in R üben Wird auch aufgenommen.

Strafbegriff für L1-Regularisierung: Die L1-Norm sieht folgendermaßen aus:

Strafbegriff für L2-Regularisierung: Die L2-Norm sieht folgendermaßen aus:

Lassen Sie uns etwas genauer untersuchen, warum die Normen L1 und L2 auf diese Weise dargestellt werden.

Definition der Lp-Norm

Vektor $ {\ bf x} $ in n Dimensionen,

{\bf x} = (x_1, \cdots, x_n)

Dann ist die $ L ^ p $ -Norm definiert als:

\| {\bf x} \|_p = (\ |x_1|^p + |x_2|^p + \cdots + |x_n|^p )^{1/p}

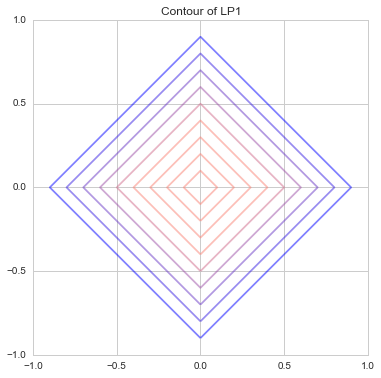
L1 Norm

Hier ist die $ L ^ 1 $ -Norm, wenn $ {\ bf x} $ zweidimensional ist, damit sie im Diagramm gezeichnet werden kann

\| {\bf x} \|_1 = |x_1| + |x_2|

Es ist nur die Addition der absoluten Werte von $ x_1 $ und $ x_2 $. Derjenige, der es mit Konturlinien darstellt So war es. Dies wird auch als [Manhattan Distance](https://ja.wikipedia.org/wiki/Manhattan Distance) bezeichnet. Da es nur vertikale und horizontale vertikale Straßen wie ein Gitter gibt, ist nur eine vertikale oder horizontale Bewegung möglich und sie bewegt sich diagonal. Es ist dasselbe wie das, das die Entfernung der Welt darstellt, die Sie nicht tun können. Mit anderen Worten, so sind die hellblauen, roten und grünen Linien alle 10 lang. Wenn Sie also denselben Abstand mit einer Linie verbinden, ist dies eine gerade Linie wie diese. Die Konturlinien in der obigen Grafik sind also rautenförmig, nicht wahr?

L2 Norm

In ähnlicher Weise ist die $ L ^ 2 $ -Norm des zweidimensionalen Vektors

\| {\bf x} \|_2 = \sqrt{|x_1|^2 + |x_2|^2}

ist. Dies ist die bekannte euklidische Distanz. Da der Abstand vom Ursprung des Punktes auf dem Umfang immer konstant ist, zeichnet die Konturlinie einen schönen Kreis, wie unten gezeigt.

Normen bei verschiedenen ps

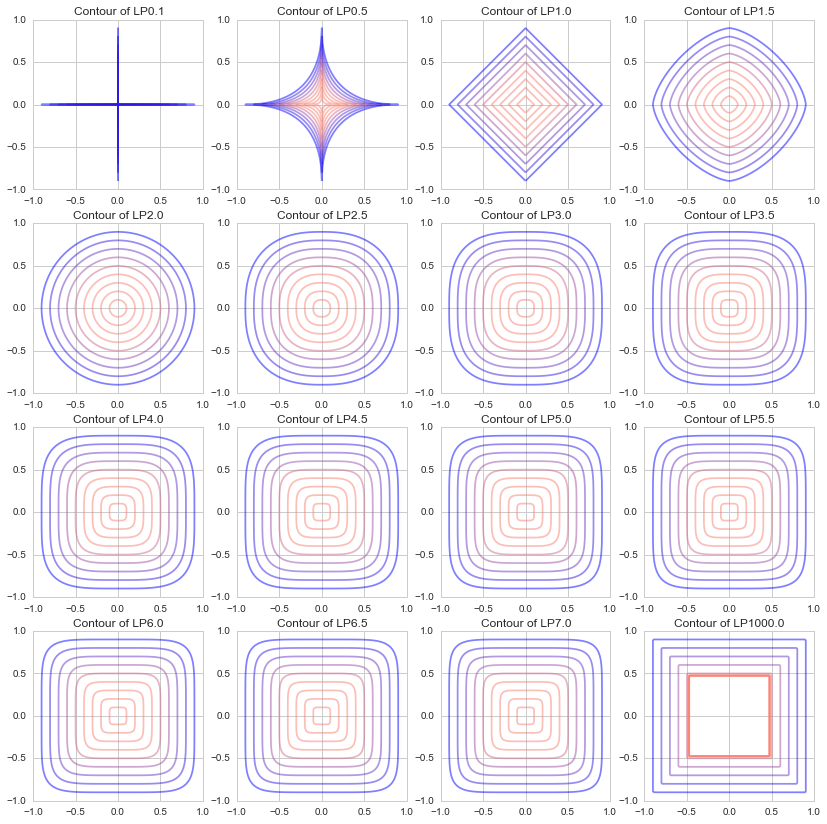
Die Normen L1 und L2 werden häufig beim maschinellen Lernen verwendet, aber zum besseren Verständnis habe ich versucht zu sehen, welche Konturlinien mit verschiedenen p-Werten gezeichnet werden.

Ich habe ein Diagramm von $ p = 1000 $ mit jeweils $ 0,5 $ von $ p = 0,1, \ p = 0,5 bis 7,5 $ gezeichnet. (Ursprünglich ist $ p $ in der Lp-Norm eine reelle Zahl von $ p \ ge1 $, aber ich habe es gewagt, 0,1 und 0,5 zu zeichnen.)

Es ist zu sehen, dass wenn p sich 0 nähert, es eine Form wie "+" wird, wenn es 1 ist, es eine Diamantform wird (ein um 45 Grad gedrehtes Quadrat), wenn es sich 2 nähert, es ein Kreis wird und wenn es sich ∞ nähert, wird es eine Form wie "□". Ich werde.

(Obwohl es außerhalb der Definition der Lp-Norm liegt, ist es eine Welt mit p = 0,1, wenn es eine Welt mit p = 0,1 gibt, sehr diagonal zu gehen: heat_smile :)

Diese L1- und L2-Normen werden angewendet und in der Lasso-Regression, der Ridge-Regression, ElasticNet usw .: Kissing_closed_eyes:

Python-Code @GitHub

Der Code für den Hauptteil dieses Artikels ist unten.

def LP(x, y, lp=1):
    x = np.abs(x) 
    y = np.abs(y)
    return (x**lp + y**lp)**(1./lp)

def draw_lp_contour(lp=1, xlim=(0, 1), ylim=(0, 1)):
    n = 201
    X, Y = np.meshgrid(np.linspace(xlim[0], xlim[1], n), np.linspace(ylim[0], ylim[1], n))
    Z = LP(X, Y, lp) 
    cm = generate_cmap(['salmon', 'salmon', 'salmon', 'salmon', 'blue'])
    interval = [i/10. -1 for i in range(20)]
    
    plt.contour(X, Y, Z, interval, alpha=0.5, cmap=cm)
    plt.title("Contour of LP{}".format(lp))
    plt.xlim(xlim[0], xlim[1])
    plt.ylim(ylim[0], ylim[1])

#Zeichnen Sie ein Diagramm mit 16 Arten von p-Werten
fig =plt.figure(figsize=(14,14))
size = 4
for i, lp in enumerate(np.r_[[0.1], np.linspace(0.5, 7, 14), [1000]]):
    plt.subplot(size, size, i+1)
    draw_lp_contour(lp, (-1, 1),(-1, 1))

Der vollständige Text des Python-Codes, der dieses Diagramm gezeichnet hat, befindet sich auf GitHub. https://github.com/matsuken92/Qiita_Contents/blob/master/General/LP-Norm.ipynb

Referenz

Wikipedia Lp Raum https://ja.wikipedia.org/wiki/Lp空間

Online Maschinelles Lernen (Machine Learning Professional Series) [Umino, Okanohara, Tokui, Tokunaga] 　http://www.kspub.co.jp/book/detail/1529038.html

Übe die L1 / L2-Regularisierung in R. 　http://tjo.hatenablog.com/entry/2015/03/03/190000

Auswirkung der L1-Regularisierung und der L2-Regularisierung auf das Regressionsmodell 　http://breakbee.hatenablog.jp/entry/2015/03/08/041411