[PYTHON] Zeitreihenanalyse Teil 4 VAR
1. Übersicht
- Nach Teil 3 (https://qiita.com/asys/items/9d40172e72dd01caa293) studiere ich basierend auf "Zeitreihenanalyse von Wirtschafts- und Finanzdaten".
- Diesmal über das VAR-Modell, das Kapitel 4 entspricht.
2. Was ist ein VAR-Modell?
- Das VAR-Modell ist eine Erweiterung des multivariaten AR-Modells.
VAR(p) : \mathbb{y}_t=\mathbb{c}+ \Phi _1 \mathbb{y} _{t-1} + \cdots + \Phi _1 \mathbb{y} _{t-p} + \epsilon _t, \quad \epsilon _t \sim W.N.(\Sigma) - Wie Sie der Formel entnehmen können, ist sie dadurch gekennzeichnet, dass sie nicht gleichzeitig andere Variablen enthält.
*Die konstante Bedingung ist, dass die Absolutwerte aller Lösungen der folgenden AR-Kennliniengleichungen größer als 1 sind.
|\mathbb{I} _n - \Phi _1 z - \cdots - \Phi _p z^p|=0
Jedoch,\mathbb{I} _n Istn\times n Ist eine Einheitsmatrix von. - Für die Modellschätzung kann jede Gleichung einzeln von OLS geschätzt werden, und sie kann durch dasselbe Verfahren wie die AR-Modellschätzung geschätzt werden.
3. Granger-Kausalität
Definition
- Die Granger-Kausalität wurde so konzipiert, dass das Vorhandensein oder Fehlen einer Kausalität nur aus den Daten zum Kausalzusammenhang zwischen Variablen bestimmt werden kann.
- Für $ \ mathbb {x} _t $ ist der zum Zeitpunkt $ t $ verfügbare Informationssatz $ \ Omega _t $, $ \ Omega _t $ minus $ \ mathbb {y} _t $ $ \ Sagen wir tilde {\ Omega} _t $. Wenn die auf $ \ Omega _t $ basierende MSE kleiner ist als die MSE für die Vorhersage des zukünftigen $ \ mathbb {x} $ basierend auf $ \ tilde {\ Omega} _t $, $ \ mathbb {y} _t $ Es gibt eine Granger-Kausalität von bis $ \ mathbb {x} _t $.
- Mit anderen Worten, es gibt eine Kausalität, wenn die Informationen in $ \ mathbb {y} _t $ die Vorhersagegenauigkeit bei der Vorhersage von $ \ mathbb {x} _t $ verbessern.
- Granger-Kausalität ist eine notwendige, aber nicht ausreichende Bedingung, damit Kausalität im üblichen Sinne existiert.
Prüfung
- Sei $ SSR _1 $ die geschätzte Restquadratsumme mit $ \ Omega _t $ und $ SSR _0 $ die geschätzte Restquadratsumme mit $ \ tilde {\ Omega} _t $.
- Berechnen Sie die $ F $ -Statistik wie folgt: $ R $ ist jedoch die Anzahl der für den Test erforderlichen Einschränkungen.
$ F \ equiv \ frac {\ frac {(SSR_0-SSR_1)} {r}} {\ frac {SSR_1} {(T-np-1)}} $ - $ rF $ folgt bekanntermaßen allmählich $ \ chi ^ 2 (r) $, wodurch die Granger-Kausalität bestimmt wird.
Analysebeispiel
Daten
- Die verwendeten Daten waren ein Datensatz namens FI2010. Von hier Sie können es herunterladen, indem Sie auf Auf diesen Datensatz frei zugreifen klicken. Unter Datenverfügbarkeit.
- Obwohl hier keine Details angegeben sind, handelt es sich um einen Datensatz mit Board-Informationen an den Börsen. Ich habe es benutzt, um mich daran zu gewöhnen, weil es ein Datensatz ist, den ich in Zukunft gerne persönlich berühren würde.
- Hier analysieren wir den Übergang der Aktienkurse (im Folgenden als Änderungsrate des mittleren Preises bezeichnet) und den Grad des Ungleichgewichts zwischen den besten Quotes. In Bezug auf die beste Quotierungsmenge zu einem bestimmten Zeitpunkt, wenn es mehr BIDs gibt, wird angenommen, dass es mehr Käufer als Verkäufer gibt, und es wird spekuliert, dass dies zu zukünftigen Aktienkurserhöhungen führen könnte.
Vorverarbeitung
#Daten lesen.
data = pd.read_csv('Train_Dst_Auction_DecPre_CF_1.txt', header=None, delim_whitespace=True)
#Die ersten 4 Zeilen sind die besten Fragen/Dies sind die Preis- und Mengenangaben für das Gebot.
#Darüber hinaus sind die ersten 3900 Spalten die Daten für die erste Ausgabe.
pr = data.iloc[:4,:3900].T
pr.columns = ['ask_p','ask_v','bid_p','bid_v']
#Berechnen Sie den mittleren Preis aus der besten ASK und dem besten BID.
pr['mid_p'] = (pr['ask_p'] + pr['bid_p']) / 2
#Berechnen Sie die Änderungsrate des mittleren Preises.
pr['p_chg'] = pr['mid_p'].pct_change()
#Berechnen Sie den Grad des Ungleichgewichts zwischen ASK- und BID-Mengen.
pr['v_imb'] = (pr['ask_v'] / pr['bid_v']).apply(np.log)
pr = pr.dropna()
#Daten lesen.
data = pd.read_csv('Train_Dst_Auction_DecPre_CF_1.txt', header=None, delim_whitespace=True)
#Die ersten 4 Zeilen sind die besten Fragen/Dies sind die Preis- und Mengenangaben für das Gebot.
#Darüber hinaus sind die ersten 3900 Spalten die Daten für die erste Ausgabe.
pr = data.iloc[:4,:3900].T
pr.columns = ['ask_p','ask_v','bid_p','bid_v']
#Berechnen Sie den mittleren Preis aus der besten ASK und dem besten BID.
pr['mid_p'] = (pr['ask_p'] + pr['bid_p']) / 2
#Berechnen Sie die Änderungsrate des mittleren Preises.
pr['p_chg'] = pr['mid_p'].pct_change()
#Berechnen Sie den Grad des Ungleichgewichts zwischen ASK- und BID-Mengen.
pr['v_imb'] = (pr['ask_v'] / pr['bid_v']).apply(np.log)
pr = pr.dropna()
-
Die Darstellung der zu verwendenden Daten ist wie folgt.

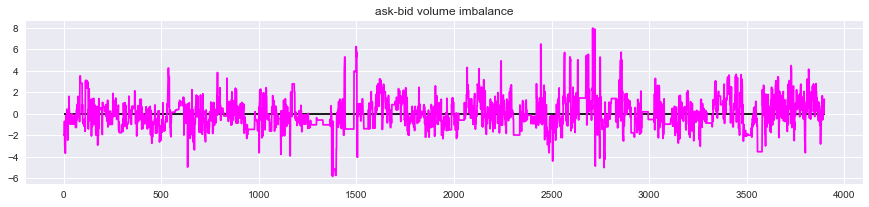
-
Der Grad des Ungleichgewichts in der besten Angebotsmenge wird berechnet als
$ \ qquad Ungleichgewicht = \ ln \ frac {V_ {ask}} {V_ {bid}} $
, und der Wert ist positiv. Im Fall von ist die Verkaufsmenge größer, und wenn der Wert negativ ist, ist die Kaufmenge größer. -
Wenn der Wert des Ungleichgewichtsgrads positiv ist und die Verkaufsmenge zum vorherigen Zeitpunkt größer ist, kann leicht überprüft werden, ob der Aktienkurs zu diesem Zeitpunkt fällt.
#Fälle, in denen es zum vorherigen Zeitpunkt mehr Verkäufer gibt
print('sell > buy ', pr.loc[pr['v_imb'].shift(-1)>1, 'p_chg'].sum())
#Fälle, in denen es zum vorherigen Zeitpunkt mehr Käufer gibt
print('sell < buy ', pr.loc[pr['v_imb'].shift(-1)<1, 'p_chg'].sum())
# sell > buy -0.0060484707428217765
# sell < buy 0.027729879129729684
Wenn es viele Verkäufe gibt, fällt der mittlere Preis im Durchschnitt, und wenn es viele Käufe gibt, steigt der mittlere Preis.
Granger-Kausaltest
- Verwenden Sie jedes Mal die bekannten Statistikmodelle.
#Laden Sie zuerst die Bibliothek und geben Sie die Daten ein.
from statsmodels.tsa.vector_ar.var_model import VAR
model = VAR(pr[['v_imb','p_chg']].values)
- Bestimmen Sie als Nächstes die Reihenfolge des Modells. Dies ist der Wert, der p in VAR (p) entspricht. Dies ist auch eine Aufnahme, wenn Sie die Bibliothek verwenden.
model.select_order(10).summary()
| AIC | BIC | FPE | HQIC | |
|---|---|---|---|---|
| 0 | -15.49 | -15.48 | 1.880e-07 | -15.49 |
| 1 | -16.29 | -16.28 | 8.405e-08 | -16.29 |
| 2 | -16.31 | -16.30 | 8.217e-08 | -16.31 |
| 3 | -16.32 | -16.30 | 8.173e-08 | -16.31 |
| 4 | -16.33* | -16.30* | 8.101e-08* | -16.32* |
| 5 | -16.33 | -16.29 | 8.103e-08 | -16.32 |
| 6 | -16.33 | -16.29 | 8.108e-08 | -16.31 |
| 7 | -16.33 | -16.28 | 8.112e-08 | -16.31 |
| 8 | -16.33 | -16.27 | 8.116e-08 | -16.31 |
| 9 | -16.33 | -16.27 | 8.111e-08 | -16.31 |
| 10 | -16.33 | -16.26 | 8.120e-08 | -16.30 |
- Bei der Betrachtung der Bestellung bis zu 10 wurde vorerst gesagt, dass $ p = 4 $ für alle vier Standardkriterien gut ist, daher wird die Bestellung auf 4 festgelegt.
- Schauen wir uns als nächstes die Granger-Kausalität an.
#Erstellen Sie ein Modell mit einer Reihenfolge von 4.
var_model = model.fit(4)
#Granger-Kausaltest. verursachen verursachen=0('v_imb')Von gebraucht=1('p_chg')Test auf Kausalität zu.
Granger = var_model.test_causality(causing=0, caused=1)
Granger.summary()
| Test statistic | Critical value | p-value | df |
|---|---|---|---|
| 9.531 | 2.373 | 0.000 | (4, 7772) |
- Betrachtet man den p-Wert, so ist er kleiner als 0,05, so dass gesagt werden kann, dass eine Granger-Kausalität vorliegt. Schließlich scheint der Grad des Ungleichgewichts des Verwaltungsrats den späteren Übergang der Aktienkurse zu beeinflussen.
- Im Gegenteil, im Gegenteil, die kausale Eigenschaft vom Übergang des Aktienkurses zum Grad des Ungleichgewichts der Kammer wurde wie folgt geprüft.
Granger = var_model.test_causality(causing=1, caused=0)
Granger.summary()
| Test statistic | Critical value | p-value | df |
|---|---|---|---|
| 0.9424 | 2.373 | 0.438 | (4, 7772) |
- Hier ist der P-Wert größer als 0,05 und das Ergebnis ist, dass keine Kausalität beobachtet wird. Es scheint, dass es einen Zusammenhang wie eine Umsatzsteigerung aufgrund des Anstiegs der Aktienkurse gibt, aber die Granger-Kausalität bestand nicht, wahrscheinlich weil die analysierte Zeitspanne zu kurz war.
4. Impulsantwortfunktion
Nicht orthogonale Impulsantwortfunktion
- In einem allgemeinen VAR-Modell die Änderung von $ y_ {i, t + k} $ nach k Periode, wenn dem störenden Term $ \ epsilon_ {jt} $ von $ y_ {jt} $ ein Schock von 1 Einheit gegeben wird Als eine Funktion.
IRF_{ij}(k)=\frac{\partial y_{i,t+k}}{\partial \epsilon_{jt}} - Es wird angenommen, dass es keine Korrelation zwischen den Störungstermen gibt, aber in Wirklichkeit gibt es viele Fälle, in denen eine Korrelation zwischen $ \ epsilon_ {it} $ und $ \ epsilon_ {jt} $ besteht. Das Problem ist, dass es nicht gut modelliert wurde.
Orthogonale Impulsantwortfunktion
- Dispersion von Störungstermen Impulsfunktion, wenn eine Co-Dispersionsmatrix trianguliert, in nicht miteinander korrelierte Störungsterme zerlegt wird und dann ein Schock von 1 Einheit auf die Störungsterme angewendet wird.
- In einem allgemeinen VAR-Modell
$ \ qquad VAR (p): \ mathbb {y} _t = \ mathbb {c} + \ Phi _1 \ mathbb {y} _ {t-1} + \ cdots + \ Phi _1 \ mathbb {y} _ {tp} + \ epsilon _t, \ quad \ epsilon _t \ sim WN (\ Sigma) $
$ A $ ist eine untere Dreiecksmatrix, deren diagonale Komponente gleich 1, $ D ist Mit $ als diagonale Matrix,
$ \ qquad \ Sigma = ADA '$
und dreieckiger Zerlegung,
$ \ qquad u \ _ t = A ^ {-1} \ epsilon \ _t $
Sie können den orthogonalen Störungsterm $ u \ _t $ in der Form> erhalten. IRF_{ij}(k)=\frac{\partial y_{i,j+k}}{\partial u_{jt}} - Aufgrund der Verwendung der dreieckigen Zerlegung ist $ \ epsilon_ {kt} $ eine lineare Summe von $ u_ {1t}, \ cdots, u_ {kt} $. Daher beeinflusst die Reihenfolge der Variablen das Ergebnis.
Analysebeispiel
- Wir werden weiterhin die für die Granger-Kausalität verwendeten Board-Daten verwenden.
#Erstellen Sie ein Modell mit einer Reihenfolge von 4.
var_model = model.fit(4)
# k=Berechnen Sie Impulsantworten bis zu 10.
IRF = var_model.irf(10)
#Zeichnen Sie die Ergebnisse. orth=Falsch bedeutet nicht orthogonal.
IRF.plot(orth=False)
plt.show()
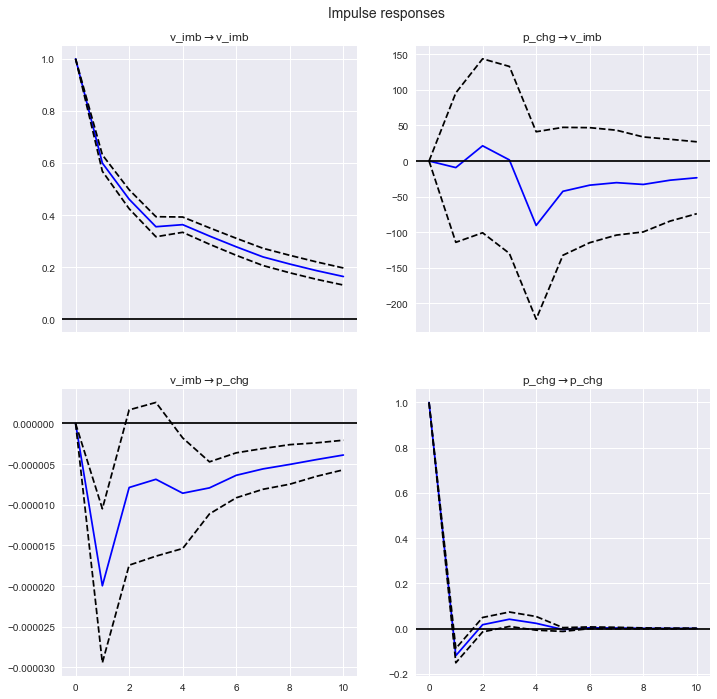
- Worauf ich achten möchte, ist die Impulsantwort von v_imb → p_chg unten links. Nach einer Periode tritt eine negative Reaktion auf, und dann nimmt die Reaktion allmählich ab. Eine Zunahme des Ungleichgewichts um eine Einheit bedeutet mehr Umsatz, was auf einen späteren Rückgang der Aktienperformance hindeutet.
5. Verteilte Zersetzung
Definition
- Das Verhältnis des orthogonalen Störungsterms $ u_ {j, t + 1}, \ cdots, u_ {j, t + k} $ von $ y_j $ zur MSE der k-Perioden-Vorhersage von $ y_i
. Es wird als relativer Dispersionsbeitragssatz (RVC) bezeichnet. *Über das n-variable VAR-Modell y_iMSE der k-Periode Zukunftsprognose von \mathbb{u}_{t+1},\cdots,\mathbb{u}_{t+k}Weil es eine lineare Summe von ist \qquad \hat{e}_{i,t+k|t}=\sum_{h=1}^{k}w_{1,t+h}^{i}u_{1,t+h}+\cdots+\sum_{h=1}^{k}w_{n,t+h}^{i}u_{n,t+h}
Dann\qquad where \quad \sigma\_l^2=E(u\_{lt}^2)
Mit\qquad RVC\_{ij}(k)=\frac{\sigma\_j^2\sum\_{h=1}^{k}(w\_{j,t+h}^i)^2}{\sum\_{l=1}^{n}\sigma\_l^2\sum\_{h=1}^{k}(w\_{l,t+h}^i)^2}
Es kann ausgedrückt werden als.
Analysebeispiel
- Verwenden Sie weiterhin FI2010-Kartendaten.
#Erstellen Sie ein Modell mit einer Reihenfolge von 4.
var_model = model.fit(4)
# k=Berechnen Sie den Dispersionsbeitragssatz bis zu 10.
FEVD = var_model.fevd(10)
#Zeichnen Sie die Ergebnisse.
FEVD.plot()
plt.show()
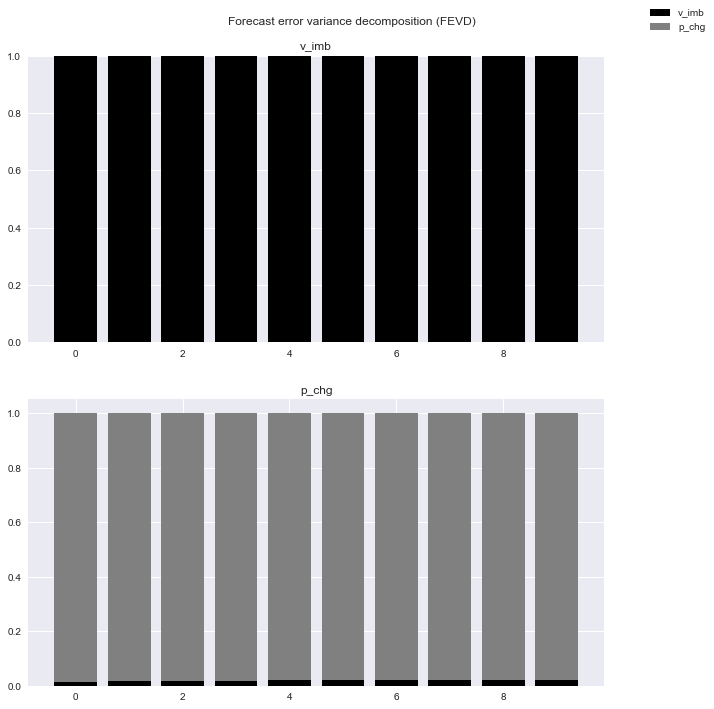
- Das ist zu schwer zu verstehen, also schauen wir uns bestimmte Zahlen an.
FEVD.summary()
| FEVD for v_imb | v_imb | p_chg |
|---|---|---|
| 0 | 1.000000 | 0.000000 |
| 1 | 0.999994 | 0.000006 |
| 2 | 0.999969 | 0.000031 |
| 3 | 0.999971 | 0.000029 |
| 4 | 0.999572 | 0.000428 |
| 5 | 0.999511 | 0.000489 |
| 6 | 0.999478 | 0.000522 |
| 7 | 0.999452 | 0.000548 |
| 8 | 0.999418 | 0.000582 |
| 9 | 0.999397 | 0.000603 |
| FEVD for p_chg | v_imb | p_chg |
|---|---|---|
| 0 | 0.012342 | 0.987658 |
| 1 | 0.018310 | 0.981690 |
| 2 | 0.018871 | 0.981129 |
| 3 | 0.019158 | 0.980842 |
| 4 | 0.019791 | 0.980209 |
| 5 | 0.020477 | 0.979523 |
| 6 | 0.020889 | 0.979111 |
| 7 | 0.021208 | 0.978792 |
| 8 | 0.021472 | 0.978528 |
| 9 | 0.021678 | 0.978322 |
- Es ist ersichtlich, dass der Beitrag von p_chg zur Streuung von v_imb sehr gering ist, was hinsichtlich der Granger-Kausalität und der Impulsantwort konsistent ist.
- Im Gegenteil, v_imb trägt ungefähr 2% zu p_chg bei. Diese Zahl ist ebenfalls sehr gering, aber der Beitrag steigt leicht an, wenn der Prognosezeitraum länger wird, was darauf hindeutet, dass es einige Zeit dauern kann, bis Änderungen der Board-Bedingungen in den Aktienkurs einbezogen werden.
Recommended Posts