[PYTHON] Einführung in die statistische Modellierung für die Datenanalyse Erweiterung des Anwendungsbereichs von GLM
Wir beschäftigen uns mit Offset-Term-Arbeiten der logistischen Regression und Poisson-Regression sowie mit GLM unter Verwendung von Normalverteilung und Gammaverteilung.
GLM, auf das verschiedene Arten von Daten angewendet werden können
Verschiedene Arten von Daten können durch GLM dargestellt werden, indem Wahrscheinlichkeitsverteilungen, Verknüpfungsfunktionen und lineare Prädiktoren kombiniert werden.
Ein Teil der Wahrscheinlichkeitsverteilung, mit der GLM in Python erstellt werden kann
Geben Sie die Zufallszahlengenerierung mit scipy.stats.X und die glm () -Familie mit statsmodels.api.families.X an.
| Wahrscheinlichkeitsverteilung | Zufällige Generierung | glm()Familienbezeichnung | Häufig verwendete Linkfunktionen | |
|---|---|---|---|---|
| (Diskret) | Binäre Verteilung | binom.rvs() | Binomial() | logit |
| Poisson-Verteilung | poisson.rvs() | Poisson() | log | |
| Negative Binomialverteilung | nbinom.rvs() | NegativeGaussian() | log | |
| (Fortlaufend) | Gammaverteilung | gamma.rvs() | Ganma() | log? |
| Normalverteilung | norm.rvs() | Gaussian() | identity |
GLM mit Binomialverteilung
Die Binomialverteilung wird verwendet, wenn ** Daten mit einer Obergrenze ** gezählt werden (Antwortvariablen sind $ y \ in \ {0, 1, 2, \ dots, N \} $).
Wenn die gleiche Behandlung auf die Versuchspersonen von N Individuen angewendet wurde, war die Reaktion bei $ y $ Individuen positiv und bei $ N-y $ Individuen negativ.
Dieses Beispiel ist
"Für jede $ i $ fiktive Pflanze $ y_i $ lebende und keimbare Samen und $ N_i-y_i $ tote Samen aus $ N_i $ beobachteten Samen."
Angenommen, insgesamt 100 Pflanzen wurden anhand der Beobachtungsdaten untersucht.
- Die Anzahl der beobachteten Samen $ N_i $ beträgt 8 für jede Person.
Über Antwortvariablen
Der mögliche Wert der Anzahl der überlebenden Samen, die die Antwortvariable ist, ist $ y_i \ in \ {0, 1, 2, 3, \ dots, 8 \} $. $ Y_i = 8 $ wenn alle am Leben sind, und $ y_i = 0 $ wenn alle tot sind.
Sei $ q_i $ die "Wahrscheinlichkeit, dass ein von einem bestimmten Individuum $ i $ erhaltener Samen lebt".
Über erklärende Variablen
Die Überlebenswahrscheinlichkeit $ q_i $ schwankt in Abhängigkeit von der Körpergröße $ x_i
>>> import pandas
>>> import matplotlib.pyplot as plt
>>> d = pandas.read_csv("data4a.csv")
>>> d.describe()
N y x
count 100 100.000000 100.000000
mean 8 5.080000 9.967200
std 0 2.743882 1.088954
min 8 0.000000 7.660000
25% 8 3.000000 9.337500
50% 8 6.000000 9.965000
75% 8 8.000000 10.770000
max 8 8.000000 12.440000
>>> plt.plot(d.x[d.f == 'C'], d.y[d.f == 'C'], 'bo')
>>> plt.plot(d.x[d.f == 'T'], d.y[d.f == 'T'], 'ro')
>>> plt.show()
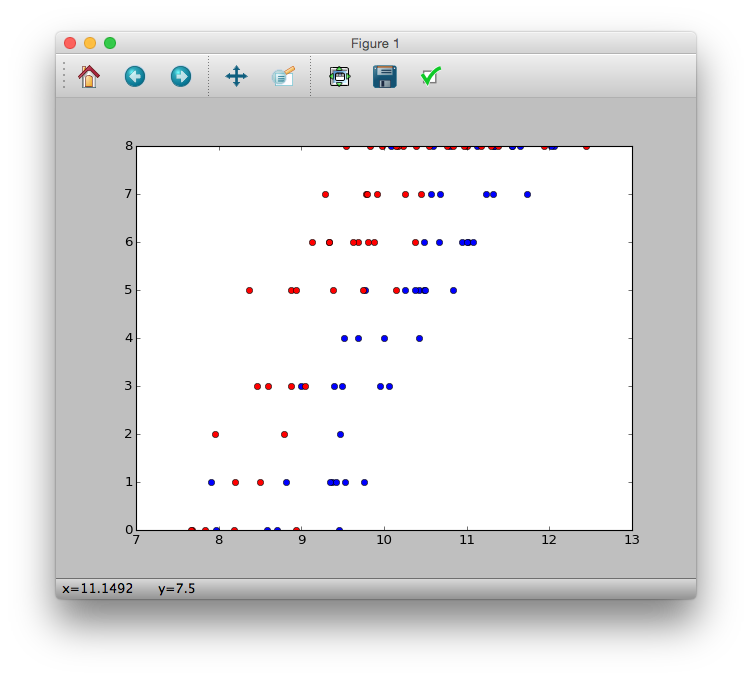
Wie Sie aus der Abbildung sehen können
- Es scheint, dass die Anzahl der überlebenden Samen $ y_i $ mit zunehmender Körpergröße $ x_i $ zunimmt.
- Es scheint, dass Dünger die Anzahl der überlebenden Samen $ y_i $ erhöht ($ f_i = T $)
Binäre Verteilung
p(y|N, q) = \left( \begin{array}{c}
N \\
y
\end{array}
\right) q^y (1-q)^{N-y}
>>> import math
>>> p = lambda y, N, q: (math.factorial(N) / (math.factorial(y) * math.factorial(N-y))) * (q ** y) * ((1-q) ** (N-y))
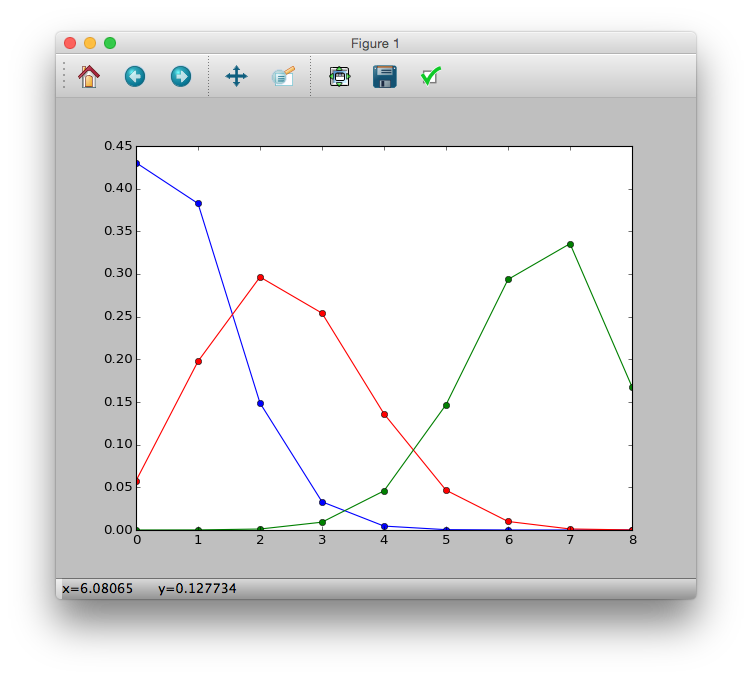
>>> p1 = [p(i, 8, 0.1) for i in y]
>>> p2 = [p(i, 8, 0.3) for i in y]
>>> p3 = [p(i, 8, 0.8) for i in y]
>>> plt.plot(y, p1, 'b-o')
>>> plt.plot(y, p2, 'r-o')
>>> plt.plot(y, p3, 'g-o')
>>> plt.show()
Logistische Regression und logistische Verknüpfungsfunktion
In der logistischen Regression
- Wahrscheinlichkeitsverteilung: ** Binäre Verteilung ** --Link-Funktion: ** Logit-Link-Funktion **
Wird genutzt.
Über ** Logistikfunktion **
q_i = logistic(z_i) = \frac{1}{1+\exp(-z_i)}
Die Variable $ z_i $ ist ein linearer Prädiktor $ z_i = \ beta_1 + \ beta_2 x_1 + \ dots $.
>>> logistic = lambda z: 1 / (1 + numpy.exp(-z))
>>> z = numpy.arange(-6, 6, 0.1)
>>> plt.plot(z, logistic(z))
>>> plt.show()

Unter der Annahme, dass die Überlebenswahrscheinlichkeit $ q_i $ eine logistische Funktion von $ z_i $ ist, ist jeder Wert des linearen Prädiktors $ z_i $ $ 0 \ leq q_i \ leq 1 $.
Unter der Annahme, dass die Überlebenswahrscheinlichkeit $ q_i $ nur von der Körpergröße $ x_i $ abhängt, ist der lineare Prädiktor $ z_i = \ beta_1 + \ beta_2 x_i $.
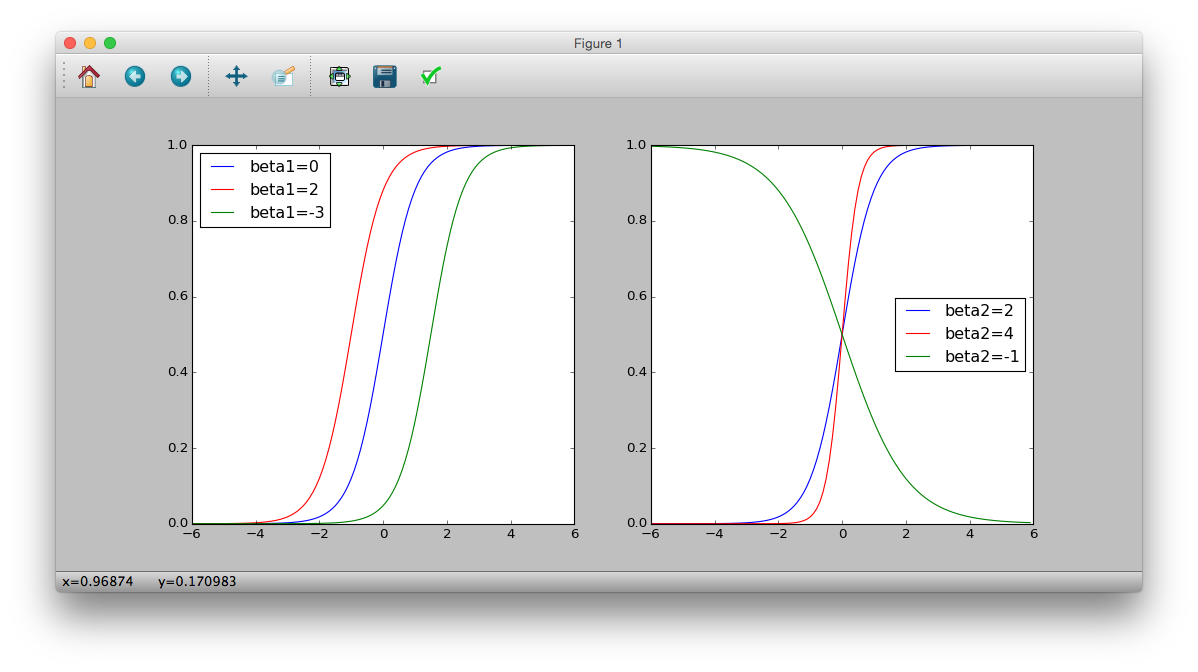
$ Q_i $ und $ x_i $ hängen von $ \ beta_1 $ und $ \ beta_2 $ ab
>>> plt.subplot(121)
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(0 + 2 * x)))
>>> plt.plot(z, logistic(z), 'b-', label='beta1=0')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(2 + 2 * x)))
>>> plt.plot(z, logistic(z), 'r-', label='beta1=2')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(-3 + 2 * x)))
>>> plt.plot(z, logistic(z), 'g-', label='beta1=-3')
>>> plt.legend(loc='middle right')
>>> plt.subplot(122)
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(2 * x)))
>>> plt.plot(z, logistic(z), 'b-', label='beta2=2')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(4 * x)))
>>> plt.plot(z, logistic(z), 'r-', label='beta2=4')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(-1 * x)))
>>> plt.plot(z, logistic(z), 'g-', label='beta2=-1')
>>> plt.legend(loc='middle right')
>>> plt.show()
Logit-Funktion
Transformieren Sie eine logistische Funktion.
\begin{eqnarray}
q_i &=& \frac{1}{1+\exp(-z_i)} \\
q_i + q_i \exp(-z_i) &=& 1 \\
1 - q_i &=& q_i \exp (-z_i)\\
\frac{1 - q_i}{q_i} &=& \exp (-z_i) \\
\log \frac{1 - q_i}{q_i} &=& -z_i \\
\log \frac{q_i}{1 - q_i} &=& z_i
\end{eqnarray}
Die linke Seite heißt ** Logit-Funktion **.
logit(q_i) = \log \frac{q_i}{1 - q_i}
- Die Logit-Funktion ist die Umkehrung der Logistikfunktion.
Parameter Schätzung
Maximieren Sie die (logische) Wahrscheinlichkeit unter der Überlebenswahrscheinlichkeit $ q_i $.
\begin{eqnarray}
L(q) &=& \prod_i p(y_i | N_i, q_i) \\
&=& \prod_i \left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right)q_i^{y_i}(1-q_i)^{N_i-y_i} \\
L(\{\beta_1, \beta_2, \beta_3\}) &=& \prod_i \left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right)q_i^{y_i}(1-q_i)^{N_i-y_i} (\because logit(q_i) = z_i = \beta_1 + \beta_2 x_i + \beta_3 d_i) \\
logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \log \left\{\left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right)q_i^{y_i}(1-q_i)^{N_i-y_i} \right\} \\
logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \left\{ \log \left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right) + \log q_i^{y_i} + \log (1-q_i)^{N_i-y_i} \right\} \\
logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \left\{ \log \left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right) + (y_i)\log q_i + (N_i-y_i)\log (1-q_i) \right\} \\
\end{eqnarray}
>>> import statsmodels.formula.api as smf
>>> import statsmodels.api as sm
>>> import pandas
>>> d = pandas.read_csv("data4a.csv")
# glm(cbind(y, N-y) ~ x + f, data=d, family=binomial)
>>> model = smf.glm('y + I(N-y) ~ x + f', data=d, family=sm.families.Binomial())
>>> fit = model.fit()
>>> fit.summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: ['y', 'I(N - y)'] No. Observations: 100
Model: GLM Df Residuals: 97
Model Family: Binomial Df Model: 2
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -133.11
Date: Sat, 06 Jun 2015 Deviance: 123.03
Time: 12:06:47 Pearson chi2: 109.
No. Iterations: 8
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -19.5361 1.414 -13.818 0.000 -22.307 -16.765
f[T.T] 2.0215 0.231 8.740 0.000 1.568 2.475
x 1.9524 0.139 14.059 0.000 1.680 2.225
==============================================================================

Über Gewinnchancen
Das Verhältnis von (Überlebenswahrscheinlichkeit) / (Nichtüberlebenswahrscheinlichkeit) heißt ** Gewinnchancen **.
\begin{eqnarray}
\frac{q_i}{1-q_i} &=& \exp(Linearer Prädiktor) \\
&=& \exp(\beta_1 + \beta_2 x_i + \beta_3 f_i) \\
&=& \exp(\beta_1)\exp(\beta_2 x_i)\exp(\beta_3 f_i)
\end{eqnarray}
Diesmal konzentrieren wir uns auf die geschätzten $ \ {\ beta_2, \ beta_3 \} $
\frac{q_i}{1-q_i} \propto \exp(1.95x_i)\exp(2.02f_i)
Und jede erklärende Variable hat eine proportionale Beziehung.
Der Effekt der Körpergröße $ x_i $ ist
\begin{eqnarray}
\frac{q_i}{1-q_i} &\propto& \exp(1.95(x_i + 1))\exp(2.02f_i) \\
&\propto& \exp(1.95x_i)\exp(1.95)\exp(2.02f_i)
\end{eqnarray}
Es ist aus diesem $ \ exp (1.95) \ Ansatz 7.03 $ mal ersichtlich. In ähnlicher Weise ist ersichtlich, dass der Befruchtungseffekt $ exp (2,02) \ ca. 7,54 $ mal beträgt.
Über Quotenverhältnis
Der Effekt des Faktors $ X $ ($ \ beta_x = 1,95 $) wird angezeigt.
\begin{eqnarray}
\frac{X Gewinnchancen}{非X Gewinnchancen} &=& \frac{\exp(X\Kugel Nicht-X gemeinsamer Teil)\times \exp(1.95 \times 1)}{\exp(X\Kugel Nicht-X gemeinsamer Teil)\times \exp(1.95 \times 0)} \\
&=& exp(1.95) \approx 7.03
\end{eqnarray}
Modellauswahl
Modellauswahl durch AIC Auswahl verschachtelter Modelle für die logistische Regression
- Konstantes Modell (nur Abschnitt) --x Modell (nur Körpergröße) --f Modell (nur Befruchtungseffekt) --x + f Modell (Körpergröße + Düngerausbringungseffekt)
Es scheint, dass R eine stepAIC () Funktion des MASS-Pakets hat.
Derzeit hat das x + f-Modell, wenn es mit dem vorherigen identisch ist, den niedrigsten AIC und ist ein gutes Modell.
Interaktionsterm
Berücksichtigen Sie den Effekt der Multiplikation der Körpergröße und den Effekt der Düngemittelanwendung. Mit anderen Worten
logit(q_i) = \beta_1 + \beta_2 x_i + \beta_3 f_i + \beta_4 x_i f_i
Denk an.
# glm(cbind(y, N-y) ~ x * f, data=d, family=binomial)
>>> model = smf.glm('y + I(N-y) ~ x * f', data=d, family=sm.families.Binomial())
>>> model.fit().summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: ['y', 'I(N - y)'] No. Observations: 100
Model: GLM Df Residuals: 96
Model Family: Binomial Df Model: 3
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -132.81
Date:Boden, 06 6 2015 Deviance: 122.43
Time: 13:44:31 Pearson chi2: 13.6
No. Iterations: 8
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -18.5233 5.335 -3.472 0.001 -28.979 -8.067
f[T.T] -0.0638 7.647 -0.008 0.993 -15.052 14.924
x 1.8525 0.525 3.529 0.000 0.824 2.881
x:f[T.T] 0.2163 0.792 0.273 0.785 -1.336 1.769
==============================================================================
Und dieses Mal stieg AIC, so dass es keine Interaktion gab.
Stoppen Sie die statistische Modellierung von Teilungswerten
Einer der Vorteile der logistischen Regression besteht darin, dass kein Teilungswert von $ (Beobachtungsdaten) / (Beobachtungsdaten) $ erstellt werden muss. Der Teilungsort wird in der Regel erstellt, wenn Sie in diesem Beispiel wissen möchten, "wovon die Überlebenswahrscheinlichkeit von Samen abhängt".
Als Nachteil
- ** Informationen gehen verloren **: Baseball-Schlagzahl als Beispiel. 300 Treffer in 1000 Schlägen und 30 Treffer in 100 Schlägen sind beide 30% Treffer, aber kann man sagen, dass sie gleichermaßen sicher sind?
- ** Wie ist die Verteilung der konvertierten Werte? **: Welcher Wahrscheinlichkeitsverteilung folgt der durch die fehlerhaften Mengen erzeugte Teilungswert?
Offset-Term-Arbeit, für die kein Teilungswert erforderlich ist
Verwenden Sie fiktive Daten wie
- 100 Vermessungsstandorte wurden rund um den Wald eingerichtet ($ i \ in \ {1, 2, \ dots, 100 \} $)
- Der Bereich $ A_i $ ist für jede Umfrageseite $ i $ unterschiedlich
- Messung der "Helligkeit" $ x_i $ der Umfrageseite $ i $
- Die Anzahl der Pflanzenindividuen $ y_i $ am Erhebungsort $ i $ wurde aufgezeichnet
- (Zweck der Analyse) Ich möchte wissen, wie die "Populationsdichte" einzelner Pflanzen am Untersuchungsort $ i $ durch die "Helligkeit" $ x_i $ beeinflusst wird.
Die Bevölkerungsdichte am Erhebungsort $ i $ mit einer Fläche von $ A_i $ beträgt
\frac{Durchschnittliche Anzahl von Personen\lambda_i}{A_i} =Bevölkerungsdichte
Ist. Die Bevölkerungsdichte ist eine positive Größe. Kombinieren Sie also die Exponentialfunktion mit der Helligkeitsabhängigkeit $ x_i $.
\begin{eqnarray}
\lambda_i &=& A_i \mal Bevölkerungsdichte\\
&=& A_i \exp(\beta_1 + \beta_2 x_i) \\
&=& \exp(\beta_1 + \beta_2 x_i + \log A_i)
\end{eqnarray}
Daher wird es zum GLM der Poisson-Verteilung der logarithmischen Verknüpfungsfunktion mit $ z_i = \ beta_1 + \ beta_2 x_i + \ log A_i $ als linearem Prädiktor.
>>> d = pandas.read_csv("data4b.csv")
>>> model = smf.glm('y ~ x', offset=numpy.log(d.A), data=d, family=sm.families.Poisson())
>>> model.fit().summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -323.17
Date: Sat, 06 Jun 2015 Deviance: 81.608
Time: 14:45:24 Pearson chi2: 81.5
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 0.9731 0.045 21.600 0.000 0.885 1.061
x 1.0383 0.078 13.364 0.000 0.886 1.191
==============================================================================
Normalverteilung und ihre Wahrscheinlichkeit
Wahrscheinlichkeitsverteilung für den Umgang mit kontinuierlichen Wertdaten in einem statistischen Modell. Es wird auch als ** Gaußsche Verteilung ** bezeichnet.
Die Parameter sind
- Durchschnittswert $ \ mu $: Kann im Bereich von $ \ pm \ infty $ frei geändert werden.
- Standardabweichung $ \ sigma $: Datenvariation kann angegeben werden.
p(y| \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp \left\{ -\frac{(y-\mu)^2}{2\sigma^2} \right\}
# y <- seq(-5, 5, 0.1)
# plot(y, dnorm(y, mean=0, sd=1), type="l")
plt.subplot(131)
plt.plot(y, sct.norm.pdf(y, loc=0, scale=1))
plt.title('$\mu=0, \sigma=1$')
plt.subplot(132)
plt.plot(y, sct.norm.pdf(y, loc=0, scale=3))
plt.title('$\mu=0, \sigma=3$')
plt.subplot(133)
plt.plot(y, sct.norm.pdf(y, loc=2, scale=1))
plt.title('$\mu=2, \sigma=1$')
plt.show()
In R ist $ \ mu $ "mean" und $ \ sigma $ ist "sd". In Python ist $ \ mu $
locund $ \ sigma $ istscale.

Angepasste Parameter für jeden. Die vertikale Achse zeigt ** Wahrscheinlichkeitsdichte **. Der rot gestrichene Bereich wird durch die Größe der Wahrscheinlichkeit dargestellt, $ 1,2 \ leq y \ leq 1,8 $ zu werden.
Wenn die Wahrscheinlichkeitsdichtefunktion der Normalverteilung $ p (y | \ mu, \ sigma) $ ist
$p(1.2 \leq y \leq 1.8| \mu, \sigma) = \int_{1.2}^{1.8}p(y| \mu, \sigma)dy
#Kumulative Verteilung
# pnorm(1.8, 0, 1) - pnorm(1.2, 0, 1)
>>> sct.norm.cdf(1.8, 0, 1) - sct.norm.cdf(1.2, 0, 1)
0.079139351108782452
Da die Wahrscheinlichkeit die Fläche ist, wird sie als Rechteck angenähert. Wenn in diesem Fall die Höhe $ p (y = 1,5 | 0, 1) $ und die Breite $ \ Delta y = 1,8-1,2 = 0,6 $ beträgt,
#Wahrscheinlichkeitsdichte
# dnorm(1.5, 0, 1) * 0.6
>>> sct.norm.pdf(1.5, 0, 1) * 0.6
0.077710557399535043
Es ist ersichtlich, dass die Annäherung erfolgt.
Höchstwahrscheinlich Schätzung
$ Probability = Basierend auf der Wahrscheinlichkeitsdichtefunktion \ times \ Delta y $.
Sei $ {\ bf Y} = \ {y_i \} $ die Höhendaten einer menschlichen Gruppe von $ N $ Personen. Die Wahrscheinlichkeit, dass a $ y_i $ $ y_i-0,5 \ Delta y \ leq y_i \ leq y_i + 0,5 \ Delta y $ ist, ist die Wahrscheinlichkeitsdichtefunktion $ p (y_i | 0, 1) $ und die Intervallbreite $ \ Delta y $. Weil es als Sitz von angenähert werden kann Die (logische) Wahrscheinlichkeitsfunktion eines statistischen Modells unter Verwendung einer Normalverteilung ist.
\begin{eqnarray}
L(\mu, \sigma) &=& \prod_i p(y_i|\mu, \sigma)\times \Delta y \\
&=& \prod_i \frac{1}{\sqrt{2\pi\sigma^2}}\exp \left\{ -\frac{(y-\mu)^2}{2\sigma^2}\right\} \Delta y \\
log L(\mu, \sigma) &=& \sum_i \left\{-\log \sqrt{2\pi\sigma^2} + \log \Delta y - \frac{(y-\mu)^2}{2\sigma^2} \right\} \\
&=& -0.5N\log(2\pi\sigma^2) + N\log \Delta y - \frac{1}{2\sigma^2}\sum_i (y-\mu)^2
\end{eqnarray}
Es wird. Beachten Sie, dass $ \ Delta y $ eine Konstante ist und den Parameter $ \ {\ mu, \ sigma \} $ nicht beeinflusst. Ignorieren Sie die obige Gleichung. Deshalb,
log L(\mu, \sigma) = -0.5N\log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_i (y-\mu)^2
Es wird.
GLM mit Gammaverteilung
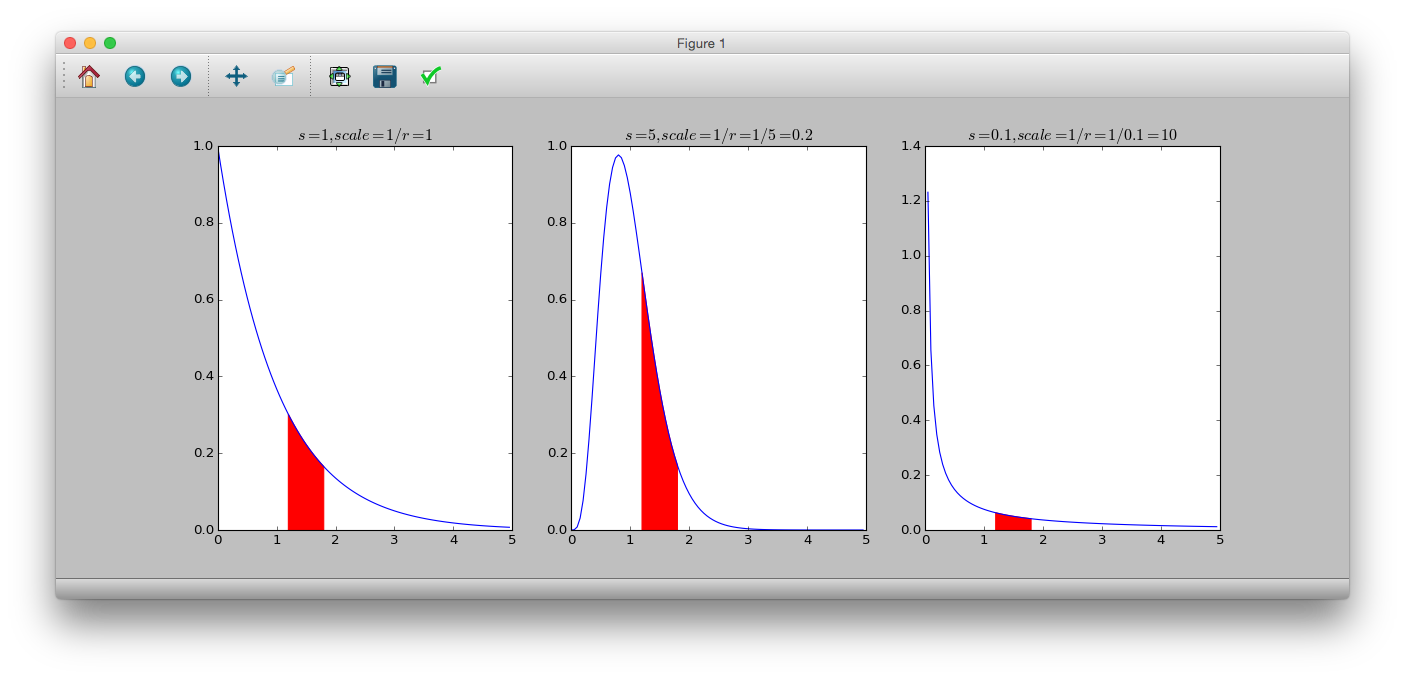
** Gammaverteilung ** ist eine kontinuierliche Wahrscheinlichkeitsverteilung, bei der der Bereich der Wahrscheinlichkeitsvariablen 0 oder mehr beträgt. Die Wahrscheinlichkeitsdichtefunktion ist.
p(y|s, r) = \frac{r^s}{\Gamma(s)}y^{s-1}\exp(-ry)
$ s $ ist der Formparameter, $ r $ ist der Ratenparameter, $ \ frac {1} {r} $ ist der Skalierungsparameter und $ \ Gamma (s) $ ist die Gammafunktion. Der Durchschnitt ist $ \ frac {s} {r} $ und die Varianz ist $ \ frac {s} {r ^ 2} $. Wenn $ s = 1 $ ist, wird auch die ** Exponentialverteilung ** erhalten.
# dgamma(y, shape, rate)
# 1/rate = scale
>>> y = numpy.arange(0, 5, 0.05)
>>> plt.subplot(131)
>>> plt.plot(y, sct.gamma.pdf(y, a=1, scale=1))
>>> plt.title('$s=1, scale=1/r=1$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=1, scale=1), color='r')
>>> plt.subplot(132)
>>> plt.plot(y, sct.gamma.pdf(y, a=5, scale=0.2))
>>> plt.title('$s=5, scale=1/r=1/5=0.2$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=5, scale=0.2), color='r')
>>> plt.subplot(133)
>>> plt.plot(y, sct.gamma.pdf(y, a=0.1, scale=10))
>>> plt.title('$s=0.1, scale=1/r=1/0.1=10$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=0.1, scale=10), color='r')
>>> plt.show()
Beispiel: Beziehung zwischen Blattgewicht und Blütengewicht einer fiktiven Pflanze
Es scheint, dass mit dem Wachstum von $ x_i $ auch $ y_i $ wächst.
\begin{eqnarray}
\mu_i &=& Ax_i^b \\
&=&\exp(a)x_i^b = \exp(a+b\log x_i) (\because A = \exp(a)) \\
\log\mu_i &=& a+blogx_i
\end{eqnarray}
>>> model = smf.glm('y ~ numpy.log(x)', data=d, family=sm.families.Gamma(link=sm.families.links.log))
>>> model.fit().summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 50
Model: GLM Df Residuals: 48
Model Family: Gamma Df Model: 1
Link Function: log Scale: 0.325084605974
Method: IRLS Log-Likelihood: 58.471
Date: Sat, 06 Jun 2015 Deviance: 17.251
Time: 20:38:39 Pearson chi2: 15.6
No. Iterations: 12
================================================================================
coef std err z P>|z| [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Intercept -1.0403 0.119 -8.759 0.000 -1.273 -0.808
numpy.log(x) 0.6832 0.068 9.992 0.000 0.549 0.817
================================================================================
get_y_mean = lambda b1, b2, x: numpy.exp(b1 + b2 * numpy.log(x))
model = smf.glm('y ~ numpy.log(x)', data=d, family=sm.families.Gamma(link=sm.families.links.log))
vc = model.fit().params
ax = plt.figure().add_subplot(111)
ax.plot(d.x, d.y, 'o')
ax.plot(d.x, get_y_mean(-1, 0.7, d.x),'--')
ax.plot(d.x, get_y_mean(vc[0], vc[1], d.x))
phi = model.fit().scale
m = get_y_mean(vc[0], vc[1], d.x)
scale = [(i * phi) for i in m]
shape = 1 / phi
def plot_pi(q):
x = numpy.r_[numpy.array(d.x), numpy.array(d.x)[::-1]]
y = numpy.r_[sct.gamma.ppf(q, a=shape, scale=scale), sct.gamma.ppf(1-q, a=shape, scale=scale)[::-1]]
pair = [(x[i], y[i]) for i in range(len(x))]
poly = plt.Polygon(pair, alpha=0.2, edgecolor='none')
return poly
ax.add_patch(plot_pi(0.05))
ax.add_patch(plot_pi(0.25))
plt.show()

Recommended Posts