Erstellen Sie in Python ein Diagramm der Standardnormalverteilung

1. Was ist Standardnormalverteilung?

Normalverteilung mit Mittelwert μ = 0, Varianz σ = 1, Das heißt, es ist eine Funktion, die durch die folgende Formel ausgedrückt wird.

f(x) =  \frac{1}{ \sqrt{2 \pi } } e^{-  \frac{x^2}{2} }

2. Erstellen Sie Ihre eigene Standardnormalverteilung

Wenn Sie f (x) selbst definieren und versuchen, [-5.0, -4.999, -4.998, ..., 4.998, 4.999, 5.0] und eine Folge von ~ 5.0 ~ 5.0, Sie erhalten ein Diagramm, das üblicherweise als Normalverteilung bezeichnet wird.

norm_original.py

# coding: utf-8
import numpy as np
import math

# f(x)Schreiben Sie selbst
f = lambda x: (math.exp(-x**2/2)) / math.sqrt(2*math.pi)

#Vektor x[-5.0, ..., 5.0]Erstellt im Abschnitt von
n = np.linspace(-5.0, 5.0, 10000)

# f(x)Holen Sie sich das Ergebnis von
p = []
for i in range(len(n)):
    p.append(f(n[i]))

#Anzeige im Diagramm
plt.scatter(n, p)
plt.show()

Ich habe eine schöne Glocke, aber es ist etwas ärgerlich, sie einzeln zu definieren. Vor allem braucht es Zeit, um den Mittelwert oder die Varianz zu ändern.

3. Verwenden Sie scipy

Mit dem Modul scipy.stats Im obigen Code (norm_original.py) kann die durch den Lambda-Ausdruck definierte Formel von der Funktion aufgerufen werden.

norm_usescipy.py

# coding: utf-8
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm

#Vektor x[-5.0, ..., 5.0]Erstellt im Abschnitt von
n = np.linspace(-5.0, 5.0, 10000)

#Durchschnitt 0,Bestimmen Sie die Wahrscheinlichkeit von x in einer Normalverteilung mit einer Standardabweichung von 1.
p = []
for i in range(len(n)):
    p.append(norm.pdf(x=n[i], loc=0, scale=1))

#Erstellen Sie ein Diagramm der Standardnormalverteilung, indem Sie die Merkmale der Zufallszahlenwahrscheinlichkeit in einem Streudiagramm anzeigen.
plt.scatter(n, p)
plt.show()

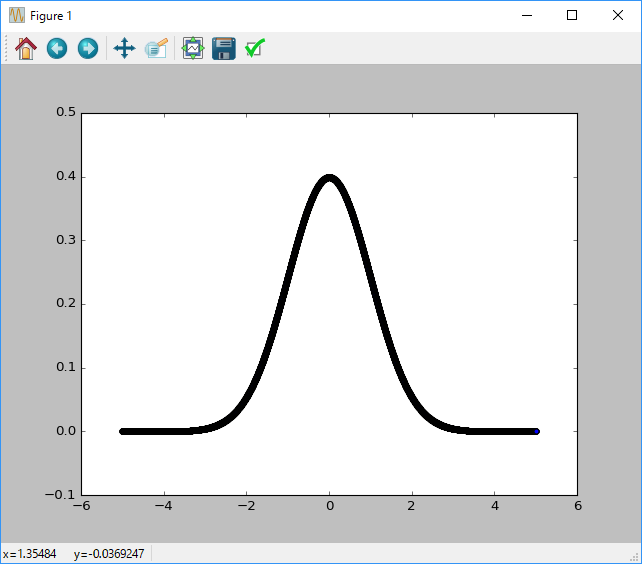
Da Sie den Mittelwert und die Varianz mit dem Argument angeben können, können Sie leicht eine Normalverteilung mit einer anderen Form erhalten.

4. Betrachten Sie die gleichzeitige Entropie aus der kumulativen Verteilungsfunktion

Im vorherigen Kapitel haben wir die normalverteilte Wahrscheinlichkeitsdichtefunktion aus scipy.stats.norm.pdf verwendet. Lassen Sie uns nun ein wenig damit spielen und die kumulative Verteilungsfunktion der Normalverteilung aus scipy.stats.norm.cdf verwenden.

Kombinierte Entropie von Wikipedia (https://ja.wikipedia.org/wiki/%E7%B5%90%E5%90%88%E3%82%A8%E3%83%B3%E3%83%88% E3% 83% AD% E3% 83% 94% E3% 83% BC) Ich werde es unter Bezugnahme auf die Beschreibung schreiben.

Die simultane Entropie (kombinierte Entropie) H (X) repräsentiert die Unsicherheit des Wertes der stochastischen Variablen X. Wenn die Wahrscheinlichkeit, dass das zu X gehörende Ereignis x eintritt, p (x) ist, ist die Entropie von X.

H(X) = - \sum_{x} p_x log_2 (p_x)

Es wird vertreten durch.

Unter der Annahme, dass die Wahrscheinlichkeit auf der Standardnormalverteilung liegt, wenn die Entropie in einem Diagramm dargestellt wird,

norm_usescipy.py

---p.append(norm.pdf(x=n[i], loc=0, scale=1))
+++p.append(norm.cdf(x=n[i], loc=0, scale=1))

Sie können H (X) so erhalten.