Google-Übersetzung von http://scikit-learn.org/stable/tutorial/statistical_inference/unsupervised_learning.html scikit-learn 0.18 Tutorial Inhaltsverzeichnis Tutorial-Tabelle zum statistischen Lernen für die wissenschaftliche Datenverarbeitung Vorherige Tutorial-Seite

Unbeaufsichtigtes Lernen: Suche nach Repräsentation von Daten

Clustering: Gruppenbeobachtungen zusammen

Durch Clustering gelöste Probleme

Wenn Sie bei einem Iris-Dataset drei Arten von Iris haben, aber keinen Zugriff auf die Kennzeichnung des Taxonomen haben, können Sie eine Clustering-Aufgabe versuchen: Beobachten Sie in gut getrennten Gruppen, die als Cluster bezeichnet werden. Teilen.

K durchschnittliche Clusterbildung

Beachten Sie, dass es viele verschiedene Clustering-Kriterien und verwandte Algorithmen gibt. Der einfachste Clustering-Algorithmus ist K Mean.

>>> from sklearn import cluster, datasets
>>> iris = datasets.load_iris()
>>> X_iris = iris.data
>>> y_iris = iris.target

>>> k_means = cluster.KMeans(n_clusters=3)
>>> k_means.fit(X_iris) 
KMeans(algorithm='auto', copy_x=True, init='k-means++', ...
>>> print(k_means.labels_[::10])
[1 1 1 1 1 0 0 0 0 0 2 2 2 2 2]
>>> print(y_iris[::10])
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]

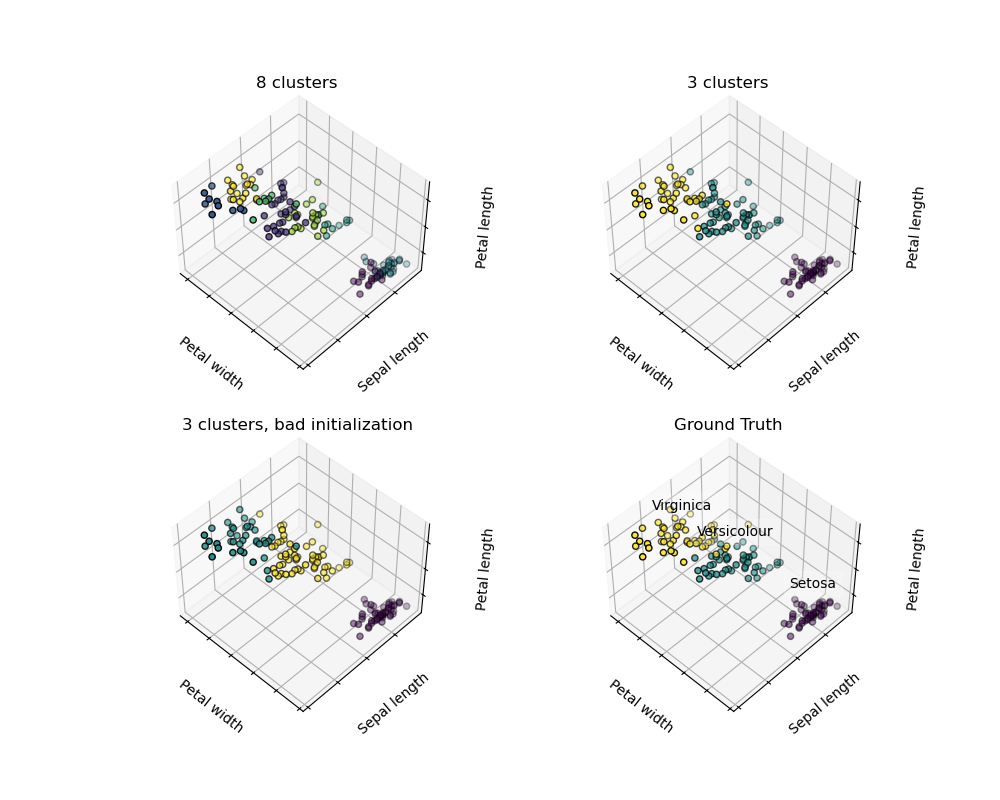
Warnung Es gibt absolut keine Garantie dafür, dass die Wahrheit auf Erden wiederhergestellt wird. Erstens ist es schwierig, die richtige Anzahl von Clustern auszuwählen. Zweitens reagiert der Algorithmus empfindlich auf Anfangswerte, und Scicit-Learn verwendet einige Tricks, um dieses Problem zu beheben, kann jedoch innerhalb des lokalen Minimums liegen.

Schlechte Initialisierung	8 Cluster	Ground truth

** Clustering-Ergebnisse nicht überinterpretieren **

Anwendungsbeispiel: Vektorquantisierung

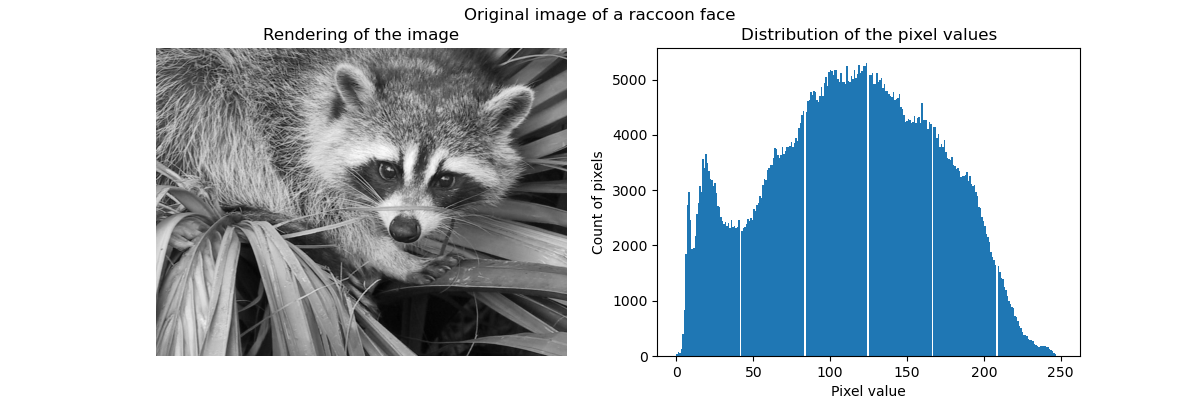
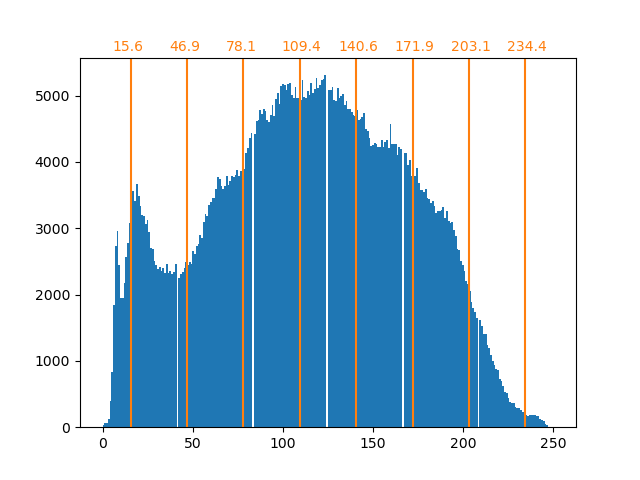
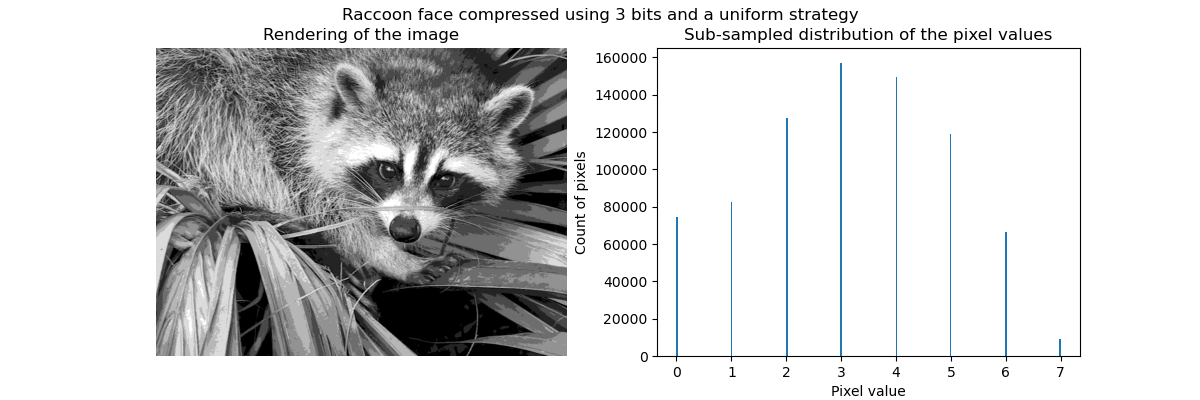
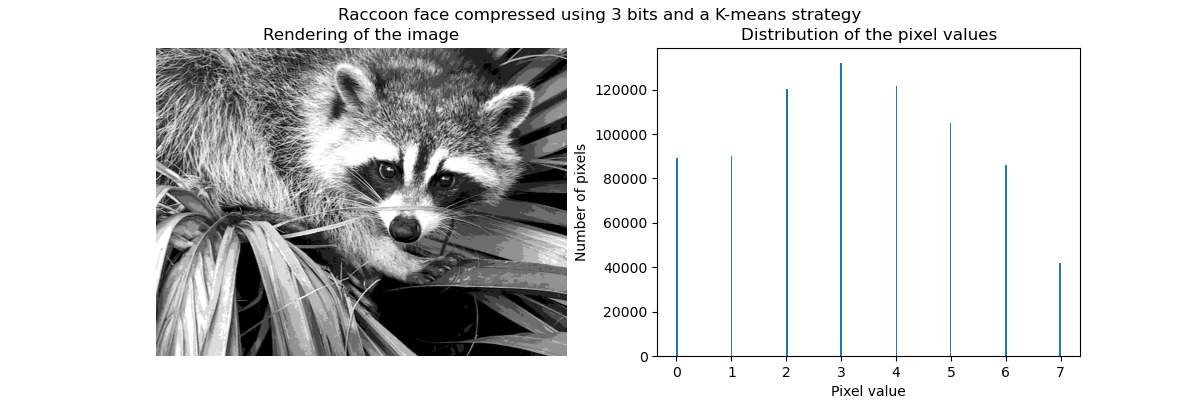
Im Allgemeinen können Clustering und K-Mittel als eine Möglichkeit angesehen werden, einige Beispiele für die Komprimierung von Informationen auszuwählen. Dieses Problem wird manchmal als Vektorquantisierung bezeichnet. Dies kann beispielsweise verwendet werden, um ein Bild zu posterisieren:

>>> import scipy as sp
>>> try:
...    face = sp.face(gray=True)
... except AttributeError:
...    from scipy import misc
...    face = misc.face(gray=True)
>>> X = face.reshape((-1, 1)) # We need an (n_sample, n_feature) array
>>> k_means = cluster.KMeans(n_clusters=5, n_init=1)
>>> k_means.fit(X) 
KMeans(algorithm='auto', copy_x=True, init='k-means++', ...
>>> values = k_means.cluster_centers_.squeeze()
>>> labels = k_means.labels_
>>> face_compressed = np.choose(labels, values)
>>> face_compressed.shape = face.shape

Rohbild	K-Quantisierung	Gleich bin	Bildhistogramm

Hierarchisches kohäsives Clustering: Ward-Methode

Die hierarchische Clustering-Methode ist eine Art Clusteranalyse, die darauf abzielt, eine Hierarchie von Clustern aufzubauen. Im Allgemeinen sind die verschiedenen Ansätze dieser Technologie

** Aggregat ** - Bottom-up-Ansatz: Jede Beobachtung beginnt mit einem eigenen Cluster, und die Cluster werden intensiv zusammengeführt, um die Bindungskriterien zu minimieren. Dieser Ansatz ist besonders interessant, wenn die interessierenden Cluster aus sehr wenigen Beobachtungen bestehen. Mit einer großen Anzahl von Clustern ist es viel rechnerisch effizienter als der k-Durchschnitt.
** Verzweigt ** - Top-Down-Ansatz: Alle Beobachtungen beginnen in einem Cluster und werden iterativ aufgeteilt, wenn Sie sich durch die Hierarchie bewegen. Um eine große Anzahl von Clustern abzuschätzen, ist dieser Ansatz langsam (für alle Beobachtungen, die als ein Cluster beginnen und rekursiv aufgeteilt werden) und statistisch böswillig.

Clustering mit eingeschränkter Konnektivität

Durch aggregiertes Clustering können Sie angeben, welche Beispiele geclustert werden sollen, indem Sie ein Verbindungsdiagramm erstellen. Das Diagramm in Scikit wird durch die benachbarte Matrix dargestellt. Oft werden spärliche Matrizen verwendet. Dies ist beispielsweise nützlich, wenn Sie Bilder gruppieren, um den verbundenen Bereich zu erhalten (auch als verbundene Komponente bezeichnet).

import matplotlib.pyplot as plt

from sklearn.feature_extraction.image import grid_to_graph
from sklearn.cluster import AgglomerativeClustering
from sklearn.utils.testing import SkipTest
from sklearn.utils.fixes import sp_version

if sp_version < (0, 12):
    raise SkipTest("Skipping because SciPy version earlier than 0.12.0 and "
                   "thus does not include the scipy.misc.face() image.")


###############################################################################
# Generate data
try:
    face = sp.face(gray=True)
except AttributeError:
    # Newer versions of scipy have face in misc
    from scipy import misc
    face = misc.face(gray=True)

# Resize it to 10% of the original size to speed up the processing
face = sp.misc.imresize(face, 0.10) / 255.

Aggregation von Merkmalen

Wir haben festgestellt, dass der Fluch der dimensionalen Zahlen, d. H. Verwendet werden kann, um unzureichende Beobachtungen im Vergleich zur Anzahl der Merkmale zu lindern. Ein anderer Ansatz besteht darin, ähnliche Funktionen zu integrieren. Agglomeration von Merkmalen. Dieser Ansatz kann durch merkmalsorientiertes Clustering erreicht werden, dh durch Clustering transponierter Daten.

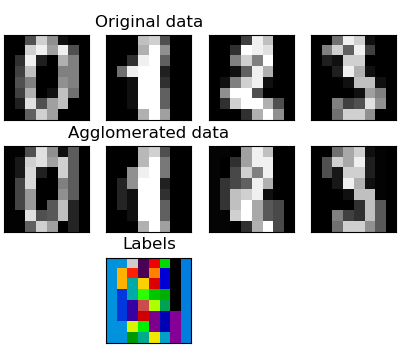
>>> digits = datasets.load_digits()
>>> images = digits.images
>>> X = np.reshape(images, (len(images), -1))
>>> connectivity = grid_to_graph(*images[0].shape)

>>> agglo = cluster.FeatureAgglomeration(connectivity=connectivity,
...                                      n_clusters=32)
>>> agglo.fit(X) 
FeatureAgglomeration(affinity='euclidean', compute_full_tree='auto',...
>>> X_reduced = agglo.transform(X)

>>> X_approx = agglo.inverse_transform(X_reduced)
>>> images_approx = np.reshape(X_approx, images.shape)

`transform` Methode und `inverse_transform` Methode

Einige Schätzer legen die Transformationsmethode offen, um beispielsweise die Anzahl der Dimensionen im Datensatz zu verringern.

Zerlegung: vom Signal zum Bauteil und Laden

Komponenten und Laden

Wenn X unsere multivariaten Daten sind, besteht das Problem, das wir zu lösen versuchen, darin, sie mit verschiedenen Beobachtungskriterien neu zu schreiben: Wir laden gerne $ L $ und $ X = LC $. Ich möchte eine Reihe von Komponenten $ C $ lernen. Es gibt verschiedene Kriterien für die Auswahl von Komponenten.

Hauptkomponentenanalyse: PCA

Die Hauptanalyse (PCA) (http://scikit-learn.org/stable/modules/decomposition.html#pca) wählt kontinuierliche Komponenten aus, die die maximale Streuung des Signals beschreiben.

Die Gruppe von Punkten, die sich über die obigen Beobachtungen erstreckt, ist in einer Richtung sehr flach. Eines der drei univariaten Merkmale kann mit den beiden anderen Funktionen fast genau berechnet werden. PCA findet Anweisungen, bei denen die Daten nicht flach sind PCA kann verwendet werden, um Daten zu transformieren, um die Dimension der Daten zu verringern, indem sie in einen Hauptunterraum projiziert werden.

>>> #Erstellen Sie ein Signal mit nur zwei gültigen Dimensionen
>>> x1 = np.random.normal(size=100)
>>> x2 = np.random.normal(size=100)
>>> x3 = x1 + x2
>>> X = np.c_[x1, x2, x3]

>>> from sklearn import decomposition
>>> pca = decomposition.PCA()
>>> pca.fit(X)
PCA(copy=True, iterated_power='auto', n_components=None, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)
>>> print(pca.explained_variance_)  
[  2.18565811e+00   1.19346747e+00   8.43026679e-32]

>>> #Wie Sie sehen können, sind nur die ersten beiden Komponenten nützlich
>>> pca.n_components = 2
>>> X_reduced = pca.fit_transform(X)
>>> X_reduced.shape
(100, 2)

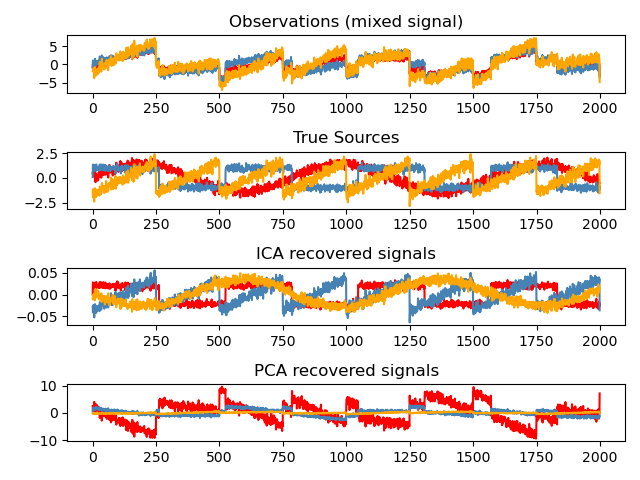
Unabhängige Komponentenanalyse: ICA

Die unabhängige Komponentenanalyse (ICA) (http://scikit-learn.org/stable/modules/decomposition.html#ica) wählt Komponenten so aus, dass die Verteilung der Komponente die maximale Menge unabhängiger Informationen enthält. .. ** Nicht-Gauß ** Unabhängige Signale können wiederhergestellt werden.

>>> # Generate sample data
>>> time = np.linspace(0, 10, 2000)
>>> s1 = np.sin(2 * time)  # Signal 1 : sinusoidal signal
>>> s2 = np.sign(np.sin(3 * time))  # Signal 2 : square signal
>>> S = np.c_[s1, s2]
>>> S += 0.2 * np.random.normal(size=S.shape)  # Add noise
>>> S /= S.std(axis=0)  # Standardize data
>>> # Mix data
>>> A = np.array([[1, 1], [0.5, 2]])  # Mixing matrix
>>> X = np.dot(S, A.T)  # Generate observations

>>> # Compute ICA
>>> ica = decomposition.FastICA()
>>> S_ = ica.fit_transform(X)  # Get the estimated sources
>>> A_ = ica.mixing_.T
>>> np.allclose(X,  np.dot(S_, A_) + ica.mean_)
True

[PYTHON] [Übersetzung] scikit-learn 0.18 Tutorial Statistisches Lernen Tutorial für die wissenschaftliche Datenverarbeitung Unbeaufsichtigtes Lernen: Suche nach Datendarstellung