[PYTHON] [Übersetzung] scikit-learn 0.18 Tutorial Statistisches Lernen Tutorial für die wissenschaftliche Datenverarbeitung Überwachtes Lernen: Vorhersage von Ausgabevariablen aus hochdimensionalen Beobachtungen
Google-Übersetzung von http://scikit-learn.org/0.18/tutorial/statistical_inference/supervised_learning.html scikit-learn 0.18 Tutorial Inhaltsverzeichnis Tutorial-Tabelle zum statistischen Lernen für die wissenschaftliche Datenverarbeitung Vorherige Seite
Überwachtes Lernen: Vorhersage von Ausgabevariablen aus hochdimensionalen Beobachtungen
Probleme, die durch überwachtes Lernen gelöst werden
[Lernen mit dem Lehrer](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98%E3%81%8D%E5 % AD% A6% E7% BF% 92) ist die Verbindung zwischen den Beobachtungsdaten "X" und der externen Variablen "y" (normalerweise als "Ziel" oder "Label" bezeichnet), die Sie vorhersagen möchten. Ist zu lernen. Oft ist "y" ein eindimensionales Array der Länge "n_samples". Alle von Scikit-Learn überwachten Schätzer haben eine "Fit (X, y)" - Methode, die zum Modell passt, und eine "Vorhersage" (gibt das prädiktive Label "y" zurück, wenn die unbeschriftete Beobachtung "X" gegeben ist. Implementieren Sie die X) `-Methode.
Wortschatz: Klassifizierung und Rückgabe
Wenn die Vorhersageaufgabe darin besteht, Beobachtungen innerhalb einer Reihe von endlichen Bezeichnungen zu klassifizieren, wird die Aufgabe des "Benennens" der beobachteten Objekte mit anderen Worten als ** Klassifizierungsaufgabe ** bezeichnet. Wenn das Ziel andererseits darin besteht, eine kontinuierliche Zielvariable vorherzusagen, spricht man von einer ** Regressionsaufgabe **.
Bei der Klassifizierung mit scikit-learn ist y ein Vektor von ganzen Zahlen oder Zeichenfolgen.
Hinweis: Eine einfache Möglichkeit zum Implementieren des grundlegenden Vokabulars für maschinelles Lernen, das in scikit-learn verwendet wird, finden Sie unter Einführung in maschinelles Lernen mit dem scikit-learn-Lernprogramm. ae16bd4d93464fbfa19b) ".
Nächster und dimensionaler Fluch
Iris kategorisieren:
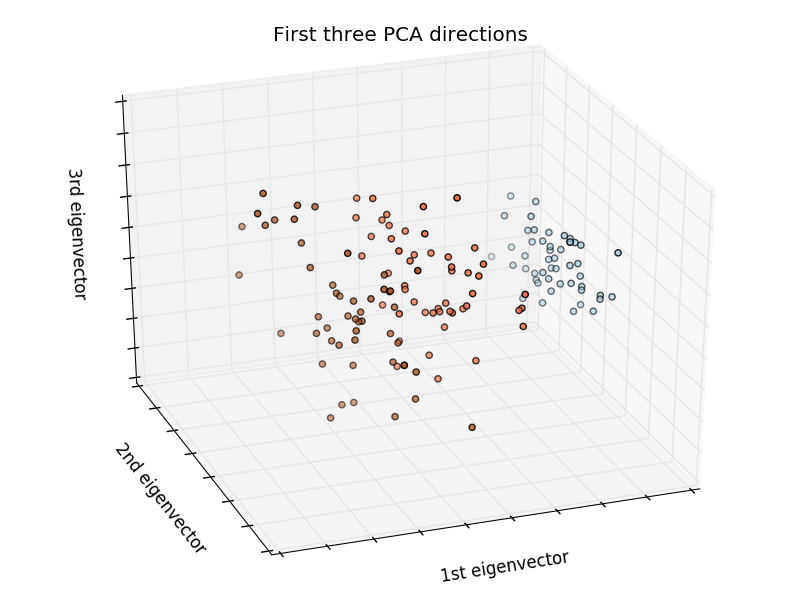
Der Iris-Datensatz ist eine Klassifizierungsaufgabe, die Iris-Typen (Setosa, Versicolour und Virginia) anhand der Länge und Breite von Blütenblättern und Blättern identifiziert.
>>> import numpy as np
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> iris_X = iris.data
>>> iris_y = iris.target
>>> np.unique(iris_y)
array([0, 1, 2])
k Nachbarschaftsklassifikator
Der einfachste mögliche Klassifikator ist die Nearest-Methode (https://en.wikipedia.org/wiki/K-nearest_neighbor_algorithm). Finden Sie bei einer neuen Stichprobe "X_test" Beobachtungen mit dem nächstgelegenen Merkmalsvektor im Trainingssatz (dh den Daten, die zum Trainieren des Schätzers verwendet wurden). (Weitere Informationen zu diesem Klassifizierertyp finden Sie im Abschnitt "Nächste Nachbarn" des Scikit-Online-Online-Handbuchs. Bitte gib mir).
Trainingsset und Testset
Während Sie mit einem Trainingsalgorithmus experimentieren, ist es wichtig, die für das Training verwendeten Daten nicht zu testen, damit Sie die Schätzerleistung für neue Daten bewerten können. Aus diesem Grund werden Datensätze häufig in Trainings- und Testdaten aufgeteilt.
KNN-Klassifizierungsbeispiel (k nächster Punkt):
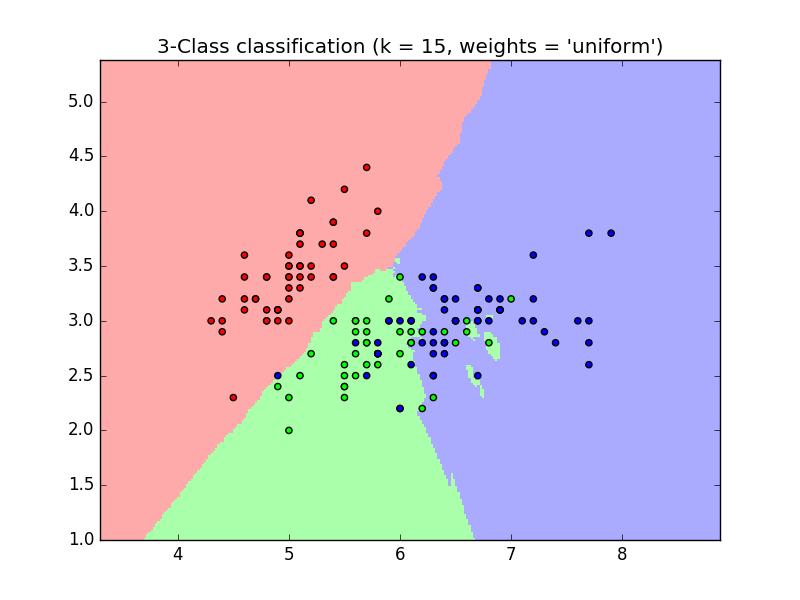
>>> #Teilen Sie die Irisdaten in Trainingsdaten und Testdaten
>>> #Zufällige Ersetzung, die die Daten zufällig teilt
>>> np.random.seed(0)
>>> indices = np.random.permutation(len(iris_X))
>>> iris_X_train = iris_X[indices[:-10]]
>>> iris_y_train = iris_y[indices[:-10]]
>>> iris_X_test = iris_X[indices[-10:]]
>>> iris_y_test = iris_y[indices[-10:]]
>>> #Erstellen Sie den nächsten Klassifikator und passen Sie ihn an
>>> from sklearn.neighbors import KNeighborsClassifier
>>> knn = KNeighborsClassifier()
>>> knn.fit(iris_X_train, iris_y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')
>>> knn.predict(iris_X_test)
array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])
>>> iris_y_test
array([1, 1, 1, 0, 0, 0, 2, 1, 2, 0])
Dimensionsfluch
Damit der Schätzer effektiv ist, muss der Abstand zwischen benachbarten Punkten je nach Problem kleiner als ein bestimmter Wert sein, $ d $. In einer Dimension erfordert dies durchschnittlich $ n ~ 1 / d $ Punkte. Im obigen $ k $ -Nachbarschaftsbeispiel werden die Daten durch eine einzelne Merkmalsgröße mit Werten im Bereich von 0 bis 1 beschrieben, und in $ n $ Trainingsbeobachtungen betragen die neuen Daten nicht mehr als $ 1 / n $. .. Wenn daher $ 1 / n $ im Vergleich zur Größe der Variation in Zwischenklassenmerkmalen klein ist, ist die Bestimmungsregel für den nächsten Nachbarn effizient. Wenn die Anzahl der Features $ p $ beträgt, benötigen Sie $ n bis 1 / d ^ p $ Punkte. Angenommen, Sie benötigen 10 Punkte in einer Dimension. Hier benötigen wir $ 10 ^ p $ Punkte in der $ p $ Dimension, um den $ [0, 1] $ Raum zu ebnen. Wenn $ p $ wächst, steigt die Anzahl der für einen guten Schätzer erforderlichen Trainingspunkte exponentiell an. Wenn beispielsweise jeder Punkt nur eine Zahl (8 Byte) ist, benötigt ein gültiger $ k $ -naher Schätzer mehr Trainingsdaten als die derzeit geschätzte Größe des gesamten Internets (± 1000 Exabyte oder mehr). .. Dies wird als Fluch der Dimension bezeichnet (https://en.wikipedia.org/wiki/Curse_of_dimensionality) und ist ein zentrales Thema, mit dem sich maschinelles Lernen befasst.
Lineares Modell: Von der Regression zur Spärlichkeit
Diabetes-Datensatz
Der Diabetes-Datensatz besteht aus 10 physiologischen Variablen (Alter, Geschlecht, Gewicht, Blutdruck) von 442 Patienten und Indikatoren für das Fortschreiten der Krankheit nach 1 Jahr:
>>> diabetes = datasets.load_diabetes()
>>> diabetes_X_train = diabetes.data[:-20]
>>> diabetes_X_test = diabetes.data[-20:]
>>> diabetes_y_train = diabetes.target[:-20]
>>> diabetes_y_test = diabetes.target[-20:]
Die aktuelle Herausforderung besteht darin, das Fortschreiten der Krankheit anhand physiologischer Variablen vorherzusagen.
Lineare Regression
LinearRegression ist die einfachste Form der Summe der Quadrate von Modellresten. Passen Sie das lineare Modell an den Datensatz an, indem Sie eine Reihe von Parametern anpassen, um es so klein wie möglich zu halten.
Lineares Modell: $ y = X \ beta + ε $
- $ X $: Daten
- $ y $: Zielvariable
- $ \ beta $: Koeffizient
- $ ε $: Beobachtungsrauschen
>>> from sklearn import linear_model
>>> regr = linear_model.LinearRegression()
>>> regr.fit(diabetes_X_train, diabetes_y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> print(regr.coef_)
[ 0.30349955 -237.63931533 510.53060544 327.73698041 -814.13170937
492.81458798 102.84845219 184.60648906 743.51961675 76.09517222]
>>> #Durchschnittlicher quadratischer Fehler
>>> np.mean((regr.predict(diabetes_X_test)-diabetes_y_test)**2)
2004.56760268...
>>> #Erklärter Varianzwert: 1 ist eine perfekte Vorhersage und 0 bedeutet, dass es keine lineare Beziehung zwischen X und y gibt.
>>> regr.score(diabetes_X_test, diabetes_y_test)
0.5850753022690...
Schrumpfen
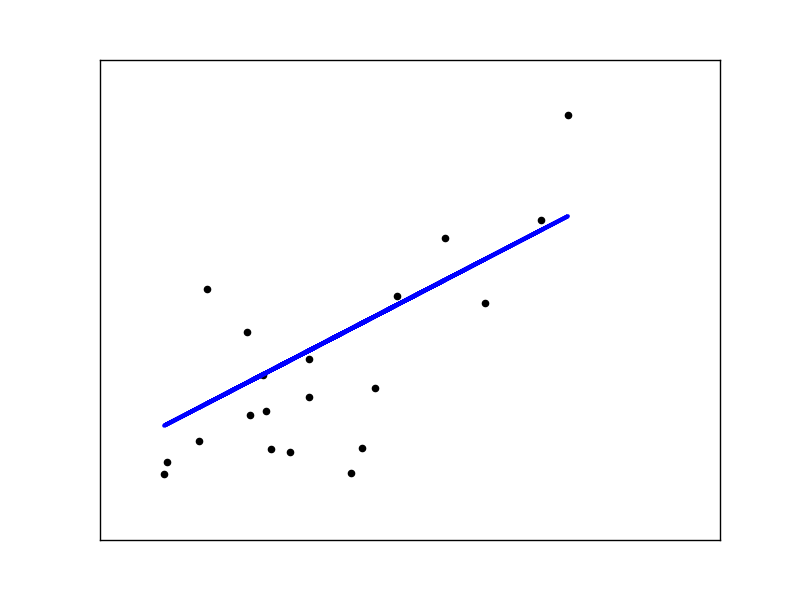
Wenn es nur wenige Datenpunkte pro Dimension gibt, verursacht das Rauschen der beobachteten Werte eine hohe Streuung.
X = np.c_[ .5, 1].T
y = [.5, 1]
test = np.c_[ 0, 2].T
regr = linear_model.LinearRegression()
import matplotlib.pyplot as plt
plt.figure()
np.random.seed(0)
for _ in range(6):
this_X = .1*np.random.normal(size=(2, 1)) + X
regr.fit(this_X, y)
plt.plot(test, regr.predict(test))
plt.scatter(this_X, y, s=3)
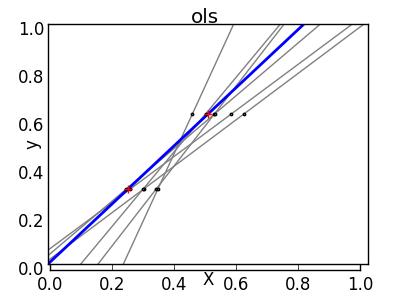
Die Lösung für statistisches Lernen höherer Ordnung besteht darin, den Regressionskoeffizienten auf Null zu reduzieren. Zwei beliebig zufällig ausgewählte Beobachtungssätze können nicht korreliert werden. Dies wird als [ridge] -Regression (http://scikit-learn.org/0.18/modules/generated/sklearn.linear_model.Ridge.html#sklearn.linear_model.Ridge) bezeichnet.
>>> regr = linear_model.Ridge(alpha=.1)
>>> plt.figure()
>>> np.random.seed(0)
>>> for _ in range(6):
... this_X = .1*np.random.normal(size=(2, 1)) + X
... regr.fit(this_X, y)
... plt.plot(test, regr.predict(test))
... plt.scatter(this_X, y, s=3)
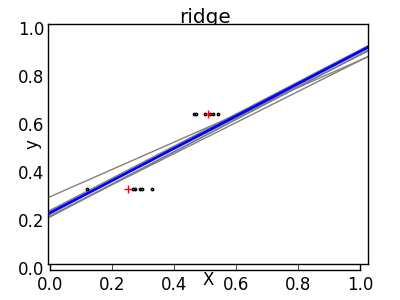
Dies ist ein Beispiel für einen Kompromiss zwischen Bias und Dispersion. Je größer der Alpha-Parameter des Kamms ist, desto höher ist die Vorspannung und desto kleiner ist die Dispersion. Sie können "Alpha" auswählen, um Fehler zu minimieren. Dieses Mal verwenden wir den Diabetes-Datensatz anstelle der synthetischen Daten.
>>> alphas = np.logspace(-4, -1, 6)
>>> from __future__ import print_function
>>> print([regr.set_params(alpha=alpha
... ).fit(diabetes_X_train, diabetes_y_train,
... ).score(diabetes_X_test, diabetes_y_test) for alpha in alphas])
[0.5851110683883..., 0.5852073015444..., 0.5854677540698..., 0.5855512036503..., 0.5830717085554..., 0.57058999437...]
** Hinweis: ** Das Erfassen von Rauschen, das verhindert, dass das Modell mit übereinstimmenden Parametern auf neue Daten verallgemeinert wird, wird als Überanpassung bezeichnet (https://en.wikipedia.org/wiki/Overfitting). Die durch die Ridge-Regression eingeführte Verzerrung wird als [Regularisierung] bezeichnet (https://en.wikipedia.org/wiki/Regularization_%28machine_learning%29).
Verdünnung
Nur für Feature 1 und Feature 2
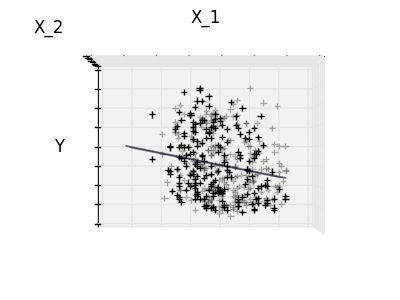
Merkmal 2 hat einen starken Koeffizienten für das vollständige Modell, aber wenn man es für Merkmal 1 betrachtet, kann man sehen, dass es sehr wenig Informationen über y vermittelt. Es wäre interessant, nur nützliche Merkmale auszuwählen und 0 für nicht vorteilhafte Merkmale wie Merkmal 2 zu setzen, um die fragliche Situation zu verbessern (dh den Fluch der Dimension zu mildern). Die Ridge-Regression reduziert ihre Beiträge, setzt sie jedoch nicht auf Null. Ein anderer Strafansatz namens Lasso (Operator für minimale absolute Reduktion und Auswahl) ermöglicht es Ihnen, einige Koeffizienten auf Null zu setzen. Eine solche Methode wird als Sparse-Methode bezeichnet, und die Spärlichkeit kann als Anwendung von Occam-Rasierapparaten angesehen werden.
>>> regr = linear_model.Lasso()
>>> scores = [regr.set_params(alpha=alpha
... ).fit(diabetes_X_train, diabetes_y_train
... ).score(diabetes_X_test, diabetes_y_test)
... for alpha in alphas]
>>> best_alpha = alphas[scores.index(max(scores))]
>>> regr.alpha = best_alpha
>>> regr.fit(diabetes_X_train, diabetes_y_train)
Lasso(alpha=0.025118864315095794, copy_X=True, fit_intercept=True,
max_iter=1000, normalize=False, positive=False, precompute=False,
random_state=None, selection='cyclic', tol=0.0001, warm_start=False)
>>> print(regr.coef_)
[ 0. -212.43764548 517.19478111 313.77959962 -160.8303982 -0.
-187.19554705 69.38229038 508.66011217 71.84239008]
Unterschiedliche Algorithmen für das gleiche Problem
Verschiedene Algorithmen können verwendet werden, um dasselbe mathematische Problem zu lösen. Beispielsweise löst das Lasso-Objekt mit Scikit-Lernfunktion das Lasso-Regressionsproblem mithilfe der effizienten Koordinatenabstiegsmethode (https://en.wikipedia.org/wiki/Coordinate_descent) für große Datenmengen. Ich werde. Scikit-learn verwendet jedoch LARS algorthm, um das Objekt LassoLars bereitzustellen. Machen. Dies ist sehr effizient bei Problemen, bei denen der geschätzte Gewichtsvektor sehr spärlich ist (Probleme mit sehr wenigen Beobachtungen).
Einstufung
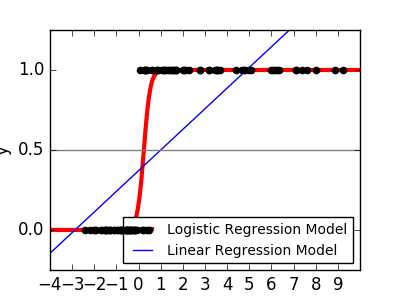
Wie bei der Irisklassifizierungsaufgabe ist die lineare Regression kein guter Ansatz, da Daten, die weit von der Entscheidungsgrenze entfernt sind, stark gewichtet werden. Der lineare Ansatz besteht darin, Sigmoid- oder Logistikfunktionen anzupassen.
y = \textrm{sigmoid}(X\beta - \textrm{offset}) + \epsilon =
\frac{1}{1 + \textrm{exp}(- X\beta + \textrm{offset})} + \epsilon
>>> logistic = linear_model.LogisticRegression(C=1e5)
>>> logistic.fit(iris_X_train, iris_y_train)
LogisticRegression(C=100000.0, class_weight=None, dual=False,
fit_intercept=True, intercept_scaling=1, max_iter=100,
multi_class='ovr', n_jobs=1, penalty='l2', random_state=None,
solver='liblinear', tol=0.0001, verbose=0, warm_start=False)
Dies wird als [LogisticRegression] bezeichnet (http://scikit-learn.org/0.18/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression).
Klassifizierung mehrerer Klassen
Wenn Sie mehrere Klassen vorhersagen müssen, können Sie häufig alle Klassifikatoren anpassen, bevor Sie die endgültige Heuristik anhand der Abstimmungsheuristik treffen.
Schrumpfung und Dünnheit aufgrund logistischer Regression
Der Parameter C steuert den Normalisierungsgrad des LogisticRegression-Objekts. Größere C-Werte führen zu einer geringeren Regularisierung. Penalty =" l2 " ergibt eine Kontraktion (dh einen nicht spärlichen Koeffizienten) und Penalty =" l2 " ergibt eine Spärlichkeit.
Übung
Versuchen Sie, Ihren numerischen Datensatz anhand des nächsten Nachbarn und eines linearen Modells zu klassifizieren. Testen Sie diese Beobachtungen und lassen Sie die letzten 10% übrig.
from sklearn import datasets, neighbors, linear_model
digits = datasets.load_digits()
X_digits = digits.data
y_digits = digits.target
Klicken Sie hier für die Antwort
Support Vector Machine (SVM)
Lineare SVM
Support-Vektor-Maschinen gehören zur diskriminanten Modellfamilie. Suchen Sie eine Kombination von Stichproben und versuchen Sie, eine Ebene zu erstellen, die den Abstand zwischen den beiden Klassen maximiert. Die Regularisierung wird durch den Parameter C eingestellt. Ein kleiner Wert für "C" bedeutet, dass viele oder alle Beobachtungen um die Trennlinie verwendet werden, um die Marge (und die Regularisierung) zu berechnen. Wenn der Wert von "C" groß ist, bedeutet dies, dass die Marge (weniger Regularisierung) mit dem beobachteten Wert nahe der Trennlinie berechnet wird.
| Nicht reguläre SVM | Regularisierte SVM(Standard) |
|---|---|
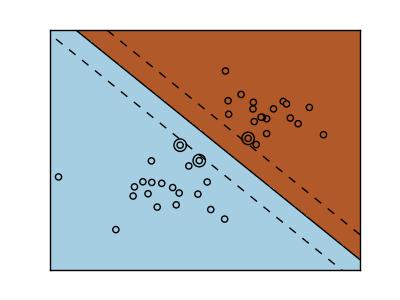 |
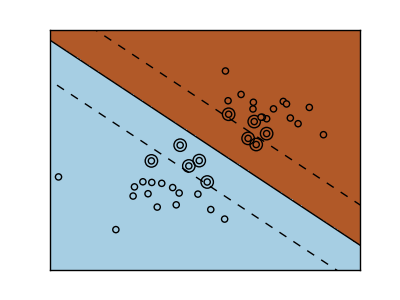 |
--Beispiel:
SVM-Regression- SVR (Support Vector Regression) -oder Klassifizierung- [SVC] Es kann unter (http://scikit-learn.org/0.18/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC) (Support Vector Classification) verwendet werden.
>>> from sklearn import svm
>>> svc = svm.SVC(kernel='linear')
>>> svc.fit(iris_X_train, iris_y_train)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma='auto', kernel='linear',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
Verwenden des Kernels
Klassen können im Feature-Space nicht immer linear getrennt werden. Die Lösung besteht darin, eine Determinante zu erstellen, die eher ein Polynom als eine lineare ist. Dies geschieht mit einem Kernel-Trick, der zur Erzeugung von Entscheidungsenergie durch Platzieren des Kernels in der Beobachtung in Betracht gezogen werden kann.
Linearer Kernel
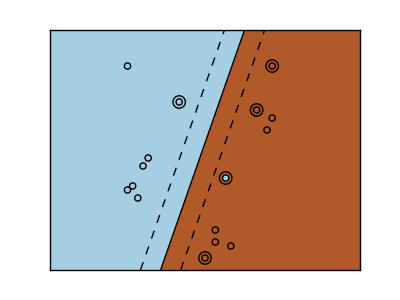
>>> svc = svm.SVC(kernel='linear')
Polygonaler Kernel
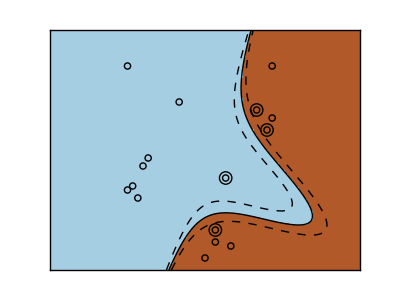
>>> svc = svm.SVC(kernel='poly',
... degree=3)
>>> # degree:Polygonreihenfolge
RBF-Kernel (Radial Basis Function)
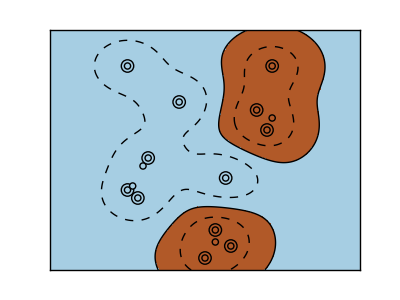
>>> svc = svm.SVC(kernel='rbf')
>>> # gamma:Die Umkehrung der Größe des Radialkerns
Interaktives Beispiel
Um svm_gui.py herunterzuladen, SVM GUI Bitte beziehen Sie sich auf. Fügen Sie mit der rechten und linken Taste Datenpunkte für beide Klassen hinzu, um sie an das Modell anzupassen, und ändern Sie die Parameter und Daten.

Übung
Versuchen Sie, Klasse 1 und Klasse 2 aus dem Iris-Dataset in einer SVM mit den ersten beiden Funktionen zu klassifizieren. Basierend auf diesen Beobachtungen werden wir die Vorhersageleistung testen und 10% jeder Klasse belassen.
WARNUNG: Klassen werden bestellt und verlassen nicht die letzten 10%. Sie testen nur in einer Klasse. Tipp: Sie können sich ein wenig ein Bild machen, indem Sie die Decision_function-Methode im Raster verwenden.
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y != 0, :2]
y = y[y != 0]
Klicken Sie hier für eine Antwort
Nächste Seite © 2010 - 2016, Entwickler von Scikit-Learn (BSD-Lizenz).
Recommended Posts