[PYTHON] Chainer und Deep Learning durch Funktionsnäherung gelernt

Lernen wir Chainer durch das Thema des Lernens der Funktion $ y = e ^ x $ durch sogenanntes Deep Learning. Das Folgende wird mit Chainer 1.6.2.1 bestätigt.

Der gleiche Inhalt wird im Jupyter-Notizbuchformat hier abgelegt. Wenn Sie ihn also beim Verschieben überprüfen möchten, lesen Sie dies bitte.

Importieren Sie zunächst die erforderlichen Module.

import numpy as np
import chainer
from chainer import cuda, Function, gradient_check, Variable, optimizers, serializers, utils
from chainer import Link, Chain, ChainList
import chainer.functions as F
import chainer.links as L

from matplotlib import pyplot as plt
%matplotlib inline

Erstellung von Lehrerdaten

Erstellen Sie zunächst eine Funktion, die Lehrerdaten ausgibt. Dieses Mal ist $ e ^ x $ der erwartete Wert für den schwebenden Bruch $ x $ von 0 bis 1,0.

Wir verwenden eine Technik namens Batch-Lernen, aber es ist praktisch, eine Funktion zu haben, die eine Reihe von $ n $ Fragen und Antworten zurückgibt.

def get_batch(n):
    x = np.random.random(n)
    y = np.exp(x)
    return x,y

print get_batch(2)

(array([ 0.25425583,  0.87356596]), array([ 1.28950165,  2.39543768]))

Neuronales Netzdesign

Als nächstes entwerfen Sie das neuronale Netz.

Da $ y = e ^ x $ eine nichtlineare Funktion ist, ist die Approximation mit nur einer linearen Funktion nicht genau genug. Wenn die Eingabe $ x $ ist, wird so etwas wie $ y = Wx + b $ als lineare Funktion bezeichnet. $ W $ wird als Gewicht und $ b $ als Bias bezeichnet, die beide nur Matrizen sind. Mit anderen Worten, es ist eine gerade Linie (wie).

Übrigens scheint es für diese lineare Operation so zu sein, dass sie als neuronales Netz bezeichnet werden kann, indem einfach eine Aktivierungsschicht durch eine nichtlineare Funktion hinzugefügt wird. Eine mehrschichtige Version davon ist ein tiefes neuronales Netz, eine nichtlineare Funktion, die beim sogenannten tiefen Lernen verwendet wird. Ich weiß nicht, wie tief es tief heißen soll, aber dieses Mal werde ich ungefähr 3 Schritte versuchen.

In einem allgemeinen Klassifizierungsproblem wird sehr oft eine nichtlineare Funktion namens relu verwendet, aber im Fall von relu verschwindet das Differential, sodass diesmal leaky_relu verwendet wird (in diesem Fall konvergierte relu nicht). .. leaky_relu ist eine einfache Funktion, die 0,2 multipliziert, wenn die Eingabe negativ ist.

Durch Optimieren der $ W- und b $ -Parameter jeder linearen Schicht werden wir versuchen, eine Funktion auszudrücken, die $ y = e ^ x $ entspricht.

Konfigurieren wir das neuronale Netz also wie folgt. L1, L2 und L3 sind jeweils lineare Funktionen. Nachdem die Abmessungen der Zwischenschicht $ h1 und h2 $ auf 16 und 32 erhöht wurden, werden sie schließlich auf eine Dimension fallen gelassen.

Im Folgenden werden die Parameter $ W, b $ von $ L_n $ als $ W_n, b_n $ ausgedrückt.

Die Tatsache, dass die mittlere Schicht (verborgene Schicht) $ h1 und h2 $ viele Kanäle haben kann (dh die Matrix der Parameter $ W_n und b_n $ ist riesig), zeigt die Ausdruckskraft des Netzwerks. Wenn sich in der Mitte kein nichtlineares Element befindet

\begin{eqnarray*}
 h_3 &=& W_3 (W_2(W_1x+b_1)+b_2)+b_3 \\
     &=& W_3 W_2 W_1 x + W_3W_2b_1 + W_3b_2 + b_3 \\
     &=& W x + b
\end{eqnarray*}

Es wird sein. $ W = W_3 W_2 W_1, b = W_3 W_2b_1 + W_3b_2 + b_3 $, aber egal wie groß die Matrix wie $ W_1, W_2, W_3 $ ist, die Parameter $ W und b $ der zusammengesetzten Funktion sind beide. Es wird ein Skalar sein. Die Tatsache, dass $ x, W, b $ alle Skalare sind, bedeutet, dass $ y = Wx + b $ eine gerade Linie ist, die nur die Steigung und den Abschnitt ändern und diese an $ e ^ x $ anpassen kann. Es ist unmöglich. Alle Parameter von $ W_1, W_2, W_3 $ werden jedoch durch Einfügen eines nichtlinearen Elements lebendig. Dies ist der Grund, warum ich am Anfang erwähnt habe: "Wenn Sie ein nichtlineares Element haben, können Sie es ein neuronales Netz nennen."

Implementierung des neuronalen Netzes

Schreiben Sie dies mit Chainer auf.

In Chainer werden Funktionen mit zu optimierenden Parametern als L (Link) und Funktionen ohne Parameter als F (Funktion) bezeichnet, um sie zu unterscheiden. Es scheint, dass dieser Bereich ein Konzept ist, das ab Version 1.5 eingeführt wurde, und ich sehe oft Tutorials, die Links zu Funktionen schreiben. Verknüpfungen werden beginnend mit einem oberen Buchstaben wie L.Linear (Eingabegröße, Ausgabegröße) definiert, und Funktionen werden beginnend mit einem unteren Buchstaben wie F.linear (x, W, b) definiert. Ältere Versionen schienen kapitalbasierte Funktionen zu verwenden, einschließlich F.Linear (), L.Linear () und F.linear (). Die beiden ersteren sind äquivalente und parametrisierte Funktionen, und die letzte ist nur eine Funktion, die Parameter angibt. Ich war ziemlich verwirrt, bevor ich das verstand.

Die Geschichte war ein wenig anders. Übergeben Sie als Nächstes eine Sammlung von Links, um eine Klasse zu erstellen, die als Kette bezeichnet wird. Wenn Sie mit dem Schreiben von Python-Klassen nicht vertraut sind, werden Sie verärgert sein, aber alles, was Sie brauchen, ist \ _ \ _ init \ _ \ _ (), um die Linkliste zu definieren, und eine Funktion, um das berechnete Diagramm an die Ausgabe zurückzugeben. Hier geben wir den Verlust als \ _ \ _ cal \ _ \ _ () zurück. Die durch \ _ \ _ call \ _ \ _ () definierte Funktion ist

m=MyChain()
loss=m(x,t)

Sie können es so nennen.

Der Punkt ist, dass die Funktion einschließlich des Parameters in \ _ \ _ init \ _ \ _ () getrennt ist und die anderen getrennt sind, damit sie in \ _ \ _ call () \ _ \ _ und anderen Methoden verwendet werden können. L.Linear () ist viel einfacher zu schreiben als TensorFlow, da Sie nur die Anzahl der Eingangskanäle und Ausgangskanäle als Parameter übergeben müssen.

class MyChain(Chain):
    def __init__(self):
        super(MyChain, self).__init__(
             l1=L.Linear(1, 16),  #1 Eingangskanal, 16 Ausgangskanäle
             l2=L.Linear(16, 32),
             l3=L.Linear(32, 1),
        )

    def __call__(self,x,t):
        #Gibt die Differenz zwischen der Netzwerkausgabe bei Eingabe von x und der Antwort t zurück.
        #Dieses Mal verwenden wir den durchschnittlichen quadratischen Fehler.
        return F.mean_squared_error(self.predict(x),t)

    def  predict(self,x):
        #Gibt die Netzwerkausgabe zurück, wenn x eingegeben wird.
        h1 = F.leaky_relu(self.l1(x))
        h2 = F.leaky_relu(self.l2(h1))
        h3 = F.leaky_relu(self.l3(h2))
        return h3

    def get(self,x):
        #Dies ist eine praktische Funktion, die die Ausgabe als reelle Zahl zurückgibt, nachdem x als reelle Zahl eingegeben wurde.
        # numpy.Es ist ein wenig verwirrend, weil es durch ndarray und Variable geht.
        return self.predict(Variable(np.array([x]).astype(np.float32).reshape(1,1))).data[0][0]

Erstellen Sie eine Instanz dieses Modells und konfigurieren Sie das Optimierungsprogramm, um die Parameter gemäß Ihrer spezifischen Strategie zu optimieren. Dieses Mal werde ich etwas verwenden, das Adam () heißt.

model = MyChain()
optimizer = optimizers.Adam()
optimizer.setup(model)

Lernen

Schließlich werden wir die Lernschleife drehen.

Als Verkettungsmethode wird ein mehrdimensionales Array (Tensor) von np.float32 mit einer dimensionalen Struktur (Stapelachse, Datenachse 1, (Datenachse 2), ..) in eine Variablenklasse konvertiert und ausgetauscht. Verwenden Sie die Datenmethode, um die tatsächliche Nummer aus der Variablenklasse abzurufen. ... Ich verstehe überhaupt nicht, wenn ich es schreibe.

Eine Charge ist eine Stichprobe von einigen aus den Lehrerdaten. Ist es einfacher, die Anzahl der Chargen als die Anzahl der Proben zu verstehen? Die Parameter werden immer für mehrere Probennummern aktualisiert, aber zusätzlich wird eine Dimension hinzugefügt, die als Anzahl der Datenkanäle bezeichnet wird, und dann werden die Dimensionen, die zum Ausdrücken der Daten erforderlich sind, hinzugefügt, wobei ein mehrdimensionales Array (Tensor) behandelt wird. Es wird sein.

In diesem Fall sind die Eingabedaten also eindimensional (Stapelachse, Datenachse) Ist in Ordnung, aber die Daten bestehen aus RGB3-Kanälen von 2D-Bildern (Stapelachse, Kanalachse = Farbachse, vertikale Achse, horizontale Achse) Pass wie. Es ist schwer zu verstehen, wenn man sich nicht daran gewöhnt. Ich stelle mir die Abbildung unten vor.

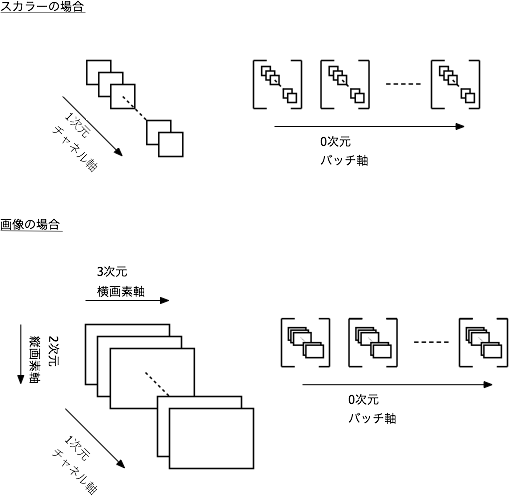
Updates lernen

1. Initialisierung der Differenzierung
2. Vorwärtsausbreitung (nach dem Netto vorwärts, um die Ausgabe zu berechnen, in diesem Fall Modell (x \ _, t \ _))
3. Rückwärtsausbreitung (Verfolgung des Netzes rückwärts, um die Differenz der Parameter zu berechnen)
4. Optimierer-Update (Aktualisieren der Parameter mithilfe der Differenzierung)

Ist eine Reihe von Flüssen. optimizer.update (Modell) erledigt dies sofort, aber ich möchte oft den Fortschritt der Weiterleitung sehen, daher schreibe ich oft alles wie folgt.

losses =[]
for i in range(10000):
    x,y = get_batch(100)
    x_ = Variable(x.astype(np.float32).reshape(100,1))
    t_ = Variable(y.astype(np.float32).reshape(100,1))
    
    model.zerograds()
    loss=model(x_,t_)
    loss.backward()
    optimizer.update()

    losses.append(loss.data)

plt.plot(losses)
plt.yscale('log')

Die horizontale Achse ist die Anzahl der Schleifen und die vertikale Achse ist die logarithmische Darstellung des Verlusts. Es wurde auf ein gutes Gefühl reduziert.

Überprüfen Sie das Ergebnis

Lassen Sie uns nun die Ausgabe des fertigen Modells überprüfen. Wenn Sie 0,2 eingeben, erhalten Sie einen Wert nahe exp (0,2)?

print model.get(0.2)
print np.exp(0.2)

1.22299
1.22140275816

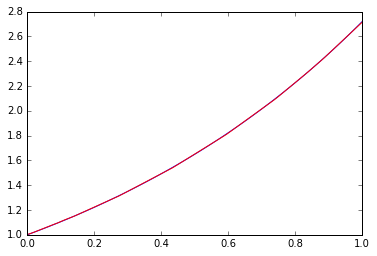
Hört sich gut an. Wie gut kann die Funktion in den Bereich von 0 bis 1 passen?

x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=model.predict(Variable(x.astype(np.float32).reshape(100,1))).data
_=plt.plot(x, p,"r")

Blau ist die richtige Antwort und Rot ist das Lernergebnis.

wohlfühlen. Diese Anpassungsleistung kann nicht allein mit der linearen Funktion erreicht werden. Es ist interessant, die Tiefe, Breite (Anzahl der Dimensionen) usw. des Netzes zu ändern, aber wie oft gesagt wird, kann bestätigt werden, dass nichtlineare Elemente und Tiefe wichtiger sind als Breite.

Beobachtung des Trainingsergebnismodells

Nun wollen wir sehen, aus welchem Koeffizienten das Modell nach dem Ergebnistraining besteht. Beispielsweise kann auf das Gewicht $ W $ der ersten Schicht 11 wie folgt zugegriffen werden.

model.l1.W.data

array([[ 0.31513408],
       [ 0.75111604],
       [ 0.48637491],
       [-1.34837043],
       [ 0.0388922 ],
       [-1.29884255],
       [-0.49960354],
       [ 0.35992688],
       [ 0.25262424],
       [-2.14205575],
       [ 0.83558381],
       [-0.61535668],
       [ 2.15679836],
       [-0.17658199],
       [-1.36228967],
       [-0.5751065 ]], dtype=float32)

Sie können dies verwenden, um eine Funktion zu erstellen, die dieselbe Ausgabe mit numpy zurückgibt, zum Beispiel:

def leaky_relu(x):
    #Einmal über ndarray, um Element-für-Element-Operationen durchzuführen
    m = np.array((x<0))
    x = np.array(x)
    return np.matrix((x*0.2)*m + x*(~m)) 

def pseudo_exp(x):
    x = np.matrix(x)
    W1 = np.matrix(model.l1.W.data)
    b1 = np.matrix(model.l1.b.data)
    W2 = np.matrix(model.l2.W.data)
    b2 = np.matrix(model.l2.b.data)
    W3 = np.matrix(model.l3.W.data)
    b3 = np.matrix(model.l3.b.data)
    
    h1 = leaky_relu(W1*x+b1.T)
    h2 = leaky_relu(W2*h1+b2.T)
    y = leaky_relu(W3*h2+b3.T)
    return y

print pseudo_exp(0.2)
print np.exp(0.2)

[[ 1.22299392]]
1.22140275816

x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=pseudo_exp(x.T)
_=plt.plot(x, p.T,"r")

Wenn Sie die Koeffizientenwerte wie model.l1.W.data so wie sie sind aufschreiben, können Sie das Trainingsergebnismodell vollständig mit nur numpy schreiben. Das Konvertieren in eine Sprache wie C oder Go sollte ebenfalls nicht schwierig sein. Nun, Chainer und Numpy sind aus Bequemlichkeitsgründen schnell genug, daher denke ich nicht, dass es nur aus Geschwindigkeitsgründen notwendig ist, in eine andere Sprache zu konvertieren, aber wenn Sie nur ein Post-Learning-Modell verwenden möchten, ist dies ein solcher Ansatz In einigen Fällen kann es nützlich sein, in ein Format zu konvertieren, das nicht von einer Bibliothek für maschinelles Lernen wie Chainer abhängt.

Beobachtung und Speicherung des Fortschritts

Wenn Sie nun versuchen, bei Jupyter Fehler zu machen, möchten Sie den Fortschritt sehen. Wenn Sie wie folgt schreiben, wird das Fortschrittsdiagramm aktualisiert. Es hängt von der Konvergenzgeschwindigkeit ab, aber ich versuche, die Anzeige alle 10 Mal zu aktualisieren.

Darüber hinaus ist das Speichern wichtig. Einmal in 100 Mal speichern.

losses =[]
from IPython import display

model = MyChain()
optimizer = optimizers.Adam()
optimizer.setup(model)

plt.hold(False)

for i in range(500):
    x,y = get_batch(100)
    x_ = Variable(x.astype(np.float32).reshape(100,1))
    t_ = Variable(y.astype(np.float32).reshape(100,1))
    
    model.zerograds()
    loss=model(x_,t_)
    loss.backward()
    optimizer.update()

    losses.append(loss.data)

    if i%10==0:
        plt.plot(losses,"b")
        plt.yscale('log')
        display.clear_output(wait=True)
        display.display(plt.gcf())
    if i%100==0:
        serializers.save_npz('my.model', model)

display.clear_output(wait=True)

Schauen wir uns die Ausgabe mit dem gespeicherten Modell an.

serializers.load_npz('my.model',model)
model.get(0.2)

1.1877015

Was ist Rückausbreitung?

Kommen wir nun zu einem kleinen Prinzip. Was bedeutet es, dass die Parameter überhaupt durch Rückausbreitung optimiert werden?

Der Einfachheit halber wird das Netzwerk nach der Rückkehr zu einer linearen Funktion ($ y = Wx + b $, $ W, b $ ist nur ein linearer Ausdruck namens Skalar) und dem Optimierer zu einem einfachen Algorithmus namens SGD zurückgeführt. Machen Sie nur eine Charge.

Anfangswerte von $ W und b $, aber standardmäßig wird in Chainer $ W $ als Zufallszahl und $ b $ als $ 0 $ ausgewählt. Hier sind der Übersichtlichkeit halber die Anfangswerte $ W = 0 und b = 0 $.

def get_batch(n):
    x=np.random.random(n)
    y= np.exp(x)
    return x,y

class LinearChain(Chain):
    def __init__(self):
        super(LinearChain, self).__init__(
             l1=L.Linear(1, 1,initialW=0.0),
        )

    def __call__(self,x,t):
        return F.mean_squared_error(self.predict(x),t)

    def  predict(self,x):
        return self.l1(x)

    def get(self,x):
        return self.predict(Variable(np.array([x]).astype(np.float32).reshape(1,1))).data[0][0]

Für die lineare Funktion $ y = Wx + b $ wird der quadratische Fehler von $ E = (y-t) ^ 2 $ als Fehlerfunktion definiert.

Die Parameter $ W $ und $ b $ werden aktualisiert, um diesen quadratischen Fehler näher an 0 zu bringen, und die Aktualisierungsrichtung wird durch die teilweise Differenzierung des Fehlers $ E $ durch jeden Parameter definiert. Mit anderen Worten

\varDelta W = \frac{\partial E}{\partial W},\quad
\varDelta b =  \frac{\partial E}{\partial b} 

ist. Dieser Wert wird als Parameterdifferenzierung bezeichnet. Diese Formel erweitern

\begin{eqnarray*}
\varDelta W &=& \frac{\partial E}{\partial y} \frac{\partial y}{\partial W} &=& 2 \left(y-t \right) x \\
\varDelta b &=& \frac{\partial E}{\partial y} \frac{\partial y}{\partial b} &=& 2 \left( y-t \right) \\
\end{eqnarray*}

Es wird sein. Durch diese Transformation kann die Differenzierung des Parameters durch die Differenz des Fehlers $ y-t $ und der bekannten Eingabe $ x $ ausgedrückt werden. Während des Berechnungsprozesses kehrt die Differenz des nachgeschalteten Fehlers zu der Differenz in den Parametern des Ausdrucks zurück, der sich stromaufwärts befindet, und wird daher als Rückausbreitung bezeichnet. $ t und x $ sind bekannt, aber $ y $ kann nur durch Berechnung der Vorwärtsausbreitung oder $ Wx + b $ erhalten werden. Wenn Sie also die Berechnung der Vorwärtsausbreitung und dann der Rückwärtsausbreitung durchführen, können Sie die Differenz zwischen den Parametern ermitteln.

In der Abbildung sieht es so aus.

Aktualisieren Sie $ W, b $ mit $ \ varDelta W, \ varDelta b $, das auf diese Weise berechnet wurde. SGD aktualisiert einfach die Parameter, indem die Steigung mit einer konstanten Lernrate $ \ alpha $ multipliziert wird. Mit anderen Worten

W \leftarrow W-\alpha \varDelta W , \quad b \leftarrow b-\alpha\varDelta b

Es wird so aktualisiert. Der Standardwert von chainer ist $ \ alpha = 0.01 $.

Lassen Sie uns diese Bewegung überprüfen.

model2 = LinearChain()
optimizer2 = optimizers.SGD()
optimizer2.setup(model2)

losses=[]
trace=[]

def scalar(v):
    #Rückgabe von Valiable auf den Skalarwert
    return v.data.ravel()[0]

for i in range(5):
    x,y = get_batch(1)
    x_ = Variable(x.astype(np.float32).reshape(1,1))
    t_ = Variable(y.astype(np.float32).reshape(1,1))
    
    model2.zerograds()
    loss=model2(x_,t_)        
    loss.backward(retain_grad=True)

    y = scalar(model2.predict(x_))
    t=scalar(t_)
    x=scalar(x_)
    W=scalar(model2.l1.W)
    b=scalar(model2.l1.b)

    #Manuell berechnetes Delta_W,delta_b
    dW_hand = 2*((y-t)*x)
    db_hand = 2*((y-t))
    
    #Delta berechnet von Chainer_W, delta_b
    dW=model2.l1.W.grad.ravel()[0]
    db=model2.l1.b.grad.ravel()[0]

  	print "======  step %d  ======" % i
    print "W,b  \t\t\t\t%2.8f, %2.8f" % (W,b)
    print "2(y-t)x,2(y-t)\t\t%2.8f, %2.8f" % (2*((y-t)*x), 2*((y-t)))
    print "⊿W,⊿b\t\t\t\t%2.8f, %2.8f" % (dW,db)   #Delta von Chainer ausgegeben_W, delta_b
    print "W-α⊿W,b-α⊿b \t\t%2.8f, %2.8f" % (W-0.01*dW,b-0.01*db)
    optimizer2.update()

======  step 0  ======
W,b  				0.00000000, 0.00000000
2(y-t)x,2(y-t)		-3.58069563, -4.46209097
⊿W,⊿b				-3.58069563, -4.46209097
W-α⊿W,b-α⊿b 		0.03580696, 0.04462091
======  step 1  ======
W,b  				0.03580695, 0.04462091
2(y-t)x,2(y-t)		-0.08072093, -1.99062216
⊿W,⊿b				-0.08072093, -1.99062216
W-α⊿W,b-α⊿b 		0.03661416, 0.06452713
======  step 2  ======
W,b  				0.03661416, 0.06452713
2(y-t)x,2(y-t)		-1.16285205, -2.84911036
⊿W,⊿b				-1.16285205, -2.84911036
W-α⊿W,b-α⊿b 		0.04824269, 0.09301824
======  step 3  ======
W,b  				0.04824268, 0.09301823
2(y-t)x,2(y-t)		-0.44180280, -2.23253369
⊿W,⊿b				-0.44180280, -2.23253369
W-α⊿W,b-α⊿b 		0.05266071, 0.11534357
======  step 4  ======
W,b  				0.05266071, 0.11534357
2(y-t)x,2(y-t)		-1.07976472, -2.70742726
⊿W,⊿b				-1.07976472, -2.70742726
W-α⊿W,b-α⊿b 		0.06345836, 0.14241784

Die folgenden zwei Punkte können bestätigt werden.

--Chainer grad gibt den gleichen Wert zurück wie die manuelle Berechnung von $ 2 (y-t) x, 2 (y-t) $ --SGD aktualisiert $ W und b $ um 0,01 Grad

Wenn Sie sich chainer Linear Source ansehen, ist es so geschrieben, dass es mehrere Ein- und Ausgänge verarbeiten kann. Es ist ein wenig schwer zu verstehen, weil es so ist, aber forward () wird als $ Wx + b $ ausgegeben, und backward () wird als Differential von $ W $ ausgegeben, indem die späteren differentiellen grad_outputs mit $ x $ multipliziert werden. Sie können sehen, dass es beschrieben wird. Die Ausgabe von backward () gibt alle Differentiale von $ x, W, b $ zurück.

Wenn Sie sich die SGD-Quelle ansehen, hat grad beim Aufruf von update () lr = 0.01. (lr ist eine Abkürzung für Lernrate) wird multipliziert und als Parameter zurückgegeben.

Lassen Sie uns nun sehen, wie das Update dazu führt, dass der optimale Wert erreicht wird.

import matplotlib.path as mpath
import matplotlib.patches as patches

#Zeichnen Sie Ross-Konturen
psize=40

W=np.linspace(-1,3,psize)
B=np.linspace(-1,3,psize)
Wm, Bm = np.meshgrid(W, B)

Z=np.zeros((psize,psize))
for w in range(psize):
    for b in range(psize):
        Z[b,w]=0.0
        for x in np.linspace(0,1,10):
            Z[b,w] += (W[w]*x+B[b]-np.exp(x))**2

plt.contourf(Wm,Bm, Z, 100,vmax=80,vmin=0)
plt.colorbar()
plt.hold(True)
    
model2 = LinearChain()
optimizer2 = optimizers.SGD()
optimizer2.setup(model2)

losses=[]
verts = [ ]
batchsize=20

for i in range(1000):

    x,y = get_batch(batchsize)
    x_ = Variable(x.astype(np.float32).reshape(batchsize,1))
    t_ = Variable(y.astype(np.float32).reshape(batchsize,1))

    #Speichern Sie den Fortschritt alle 10 Mal
    if i%10==0:
        w= model2.l1.W.data[0][0]
        b = model2.l1.b.data[0]
        verts.append((w,b))
    
    model2.zerograds()
    loss=model2(x_,t_)
    loss.backward()
    optimizer2.update(retain_grad=True)

#Zeichnen Sie den Fortschritt
xs, ys = zip(*verts)
_=plt.plot(xs, ys, 'o', lw=1, color='white') #, ms=10)

Die horizontale Achse ist $ W $ und die vertikale Achse ist $ b $. Die Konturlinien zeigen den Verlust. Sie können sehen, dass es nach unten geht.

Aufgrund der Vereinfachung ist das Anpassungsergebnis natürlich auch am optimalen Punkt gerade. Es ist das kleinste Quadrat in der Nähe der geraden Linie. Es ist unten gezeigt.

x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=model2.predict(Variable(x.astype(np.float32).reshape(100,1))).data
_=plt.plot(x, p,"r")

Mit dem Obigen haben wir gelernt, wie man Chainer verwendet, indem wir das neuronale Netz optimiert haben, das sich der Funktion $ y = e ^ x $ annähert. Es ist nur eine Berührung, aber ich habe das Prinzip der Optimierung und den Ablauf angesprochen.