Deep Learing

Perzeptron

Hintergrund

Dieses Programm wurde 1957 von einem Forscher namens Rosenblatt in den Vereinigten Staaten entwickelt. Perceptron ist der Ursprung des neuronalen Netzwerks.

Was ist Perceptron?

Es empfängt mehrere Signale als Ein- und Ausgänge eines Signals. Das Signal von Perceptron ist "1 oder 0". Das Perceptron, das die beiden Signale als Eingänge empfängt, ist wie folgt.

alt

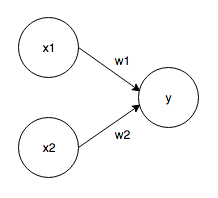
Eingangssignal: x1, x2 Ausgangssignal: y Gewichte: w1, w2 Wenn das Eingangssignal an das Neuron gesendet wird, wird jedes mit einem eindeutigen Gewicht multipliziert, und 1 wird nur ausgegeben, wenn die Summe den Grenzwert (Schwellenwert, θ) überschreitet.

f(x) = \left\{
\begin{array}{ll}
0 & (w1x1 + w2x2 \leq θ) \\
1 & (w1x1 + w2x2 \gt θ)
\end{array}
\right.

Implementierung von Perceptron

Am Beispiel des UND-Gatters ...

def AND(x1,x2):
    w1,w2,theta = 0.5,0.5,0.7
    tmp = x1*w1 + x2*w2
    if tmp <= theta:
        return 0
    elif tmp > theta:
        return 1

Voreingenommenheit einführen

Transformiere die obige Gleichung mit θ als -b

f(x) = \left\{
\begin{array}{ll}
0 & (b + w1x1 + w2x2 \leq 0) \\
1 & (b + w1x1 + w2x2 \gt 0)
\end{array}
\right.

Das UND-Gatter sieht so aus

import numpy as np
def AND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([0.5,0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

Das NAND-Gatter sieht so aus

import numpy as np
def AND(x1,x2):
    x = np.array([x1,x2])
    w = np.array([-0.5,-0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

Das ODER-Gatter sieht so aus

import numpy as np
def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w * x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

Unterschied in der Arbeit

Gewicht => Steuern Sie die Wichtigkeit des Eingangssignals Vorspannung => Steuert die Zündfreundlichkeit

Die Grenzen von Perceptron

Percepton kann keine XOR-Gatter darstellen. Es kann jedoch durch ** Stapeln von Schichten ** ausgedrückt werden.

def XOR(x1,x2):
    s1 = NAND(x1,x2)
    s2 = OR(x1,x2)
    y = AND(s1,s2)
    return y

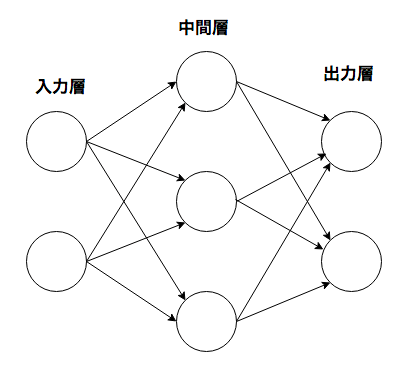
neurales Netzwerk

Es hat die Eigenschaft, dass entsprechende Gewichtsparameter automatisch aus den Daten gelernt werden können. alt

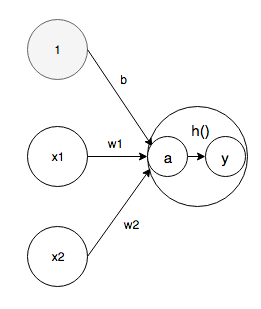
Aktivierungsfunktion

Die Aktivierungsfunktion ist eine Funktion, die die Summe der Eingangssignale in Ausgangssignale umwandelt. In einem neuronalen Netzwerk muss eine nichtlineare Funktion verwendet werden.

a = b + w1x1 + w2x2 \\
y = h(a)

alt

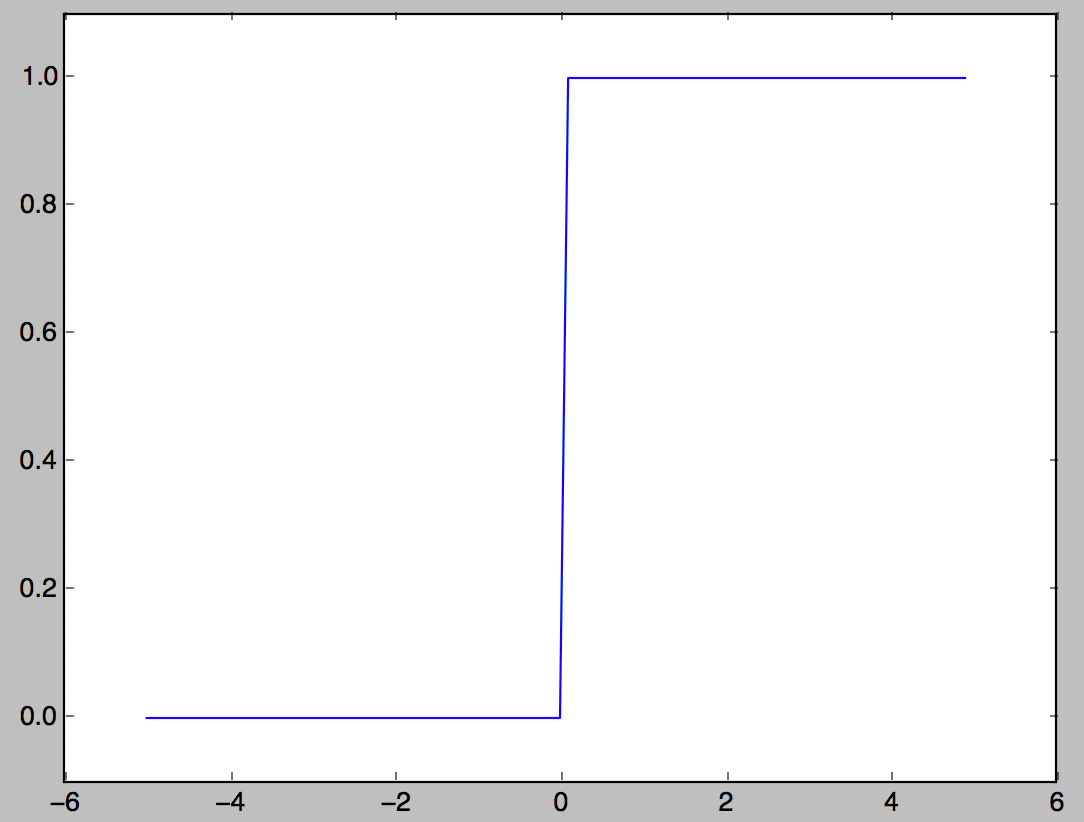
Stufenfunktion

Eine der Aktivierungsfunktionen, die 1 ausgibt, wenn der Eingang 0 überschreitet, und andernfalls 0 ausgibt.

import numpy as np
import matplotlib.pylab as plt
def step_function(x):
    y = x > 0
    return y.astype(np.int)

x = np.arange(-5.0,5.0,0.1)
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

alt

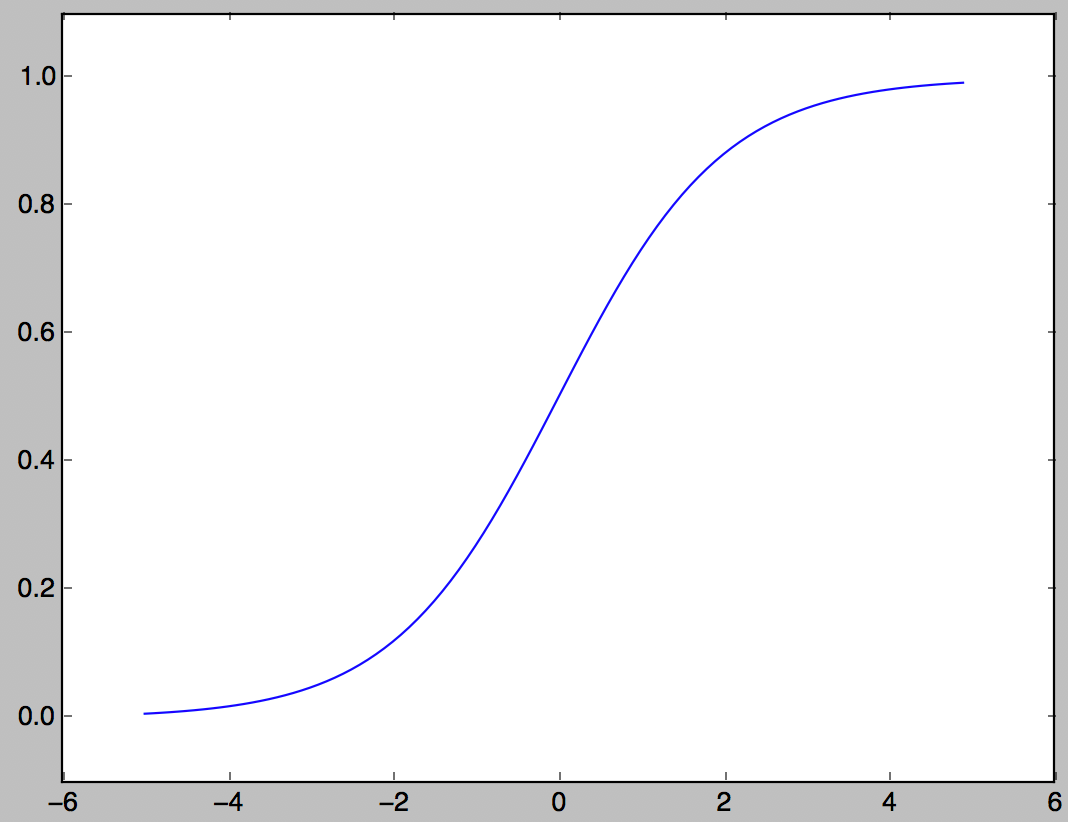
Sigmaid-Funktion

Eine der Aktivierungsfunktionen, die häufig in neuronalen Netzen verwendet werden.

h(x) = \frac{1}{1+e^{-x}}

import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
    return 1/(1+np.exp(-x))

x = np.arange(-5.0,5.0,0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()

alt

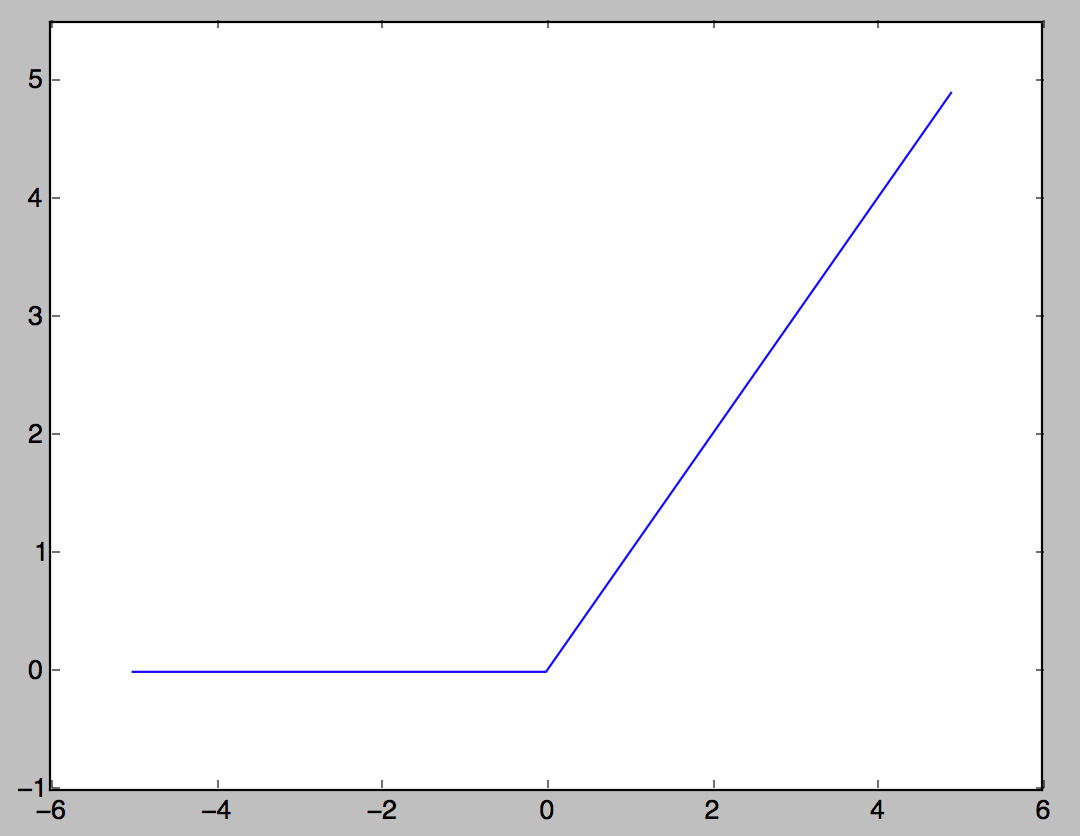
ReLU-Funktion

Aktivierungsfunktion, die heutzutage häufig verwendet wird. Wenn der Eingang 0 überschreitet, wird der Eingang so ausgegeben, wie er ist, und wenn er 0 oder weniger ist, wird 0 ausgegeben.

h(x) = \left\{
\begin{array}{ll}
x & (x \gt 0) \\
0 & (x \leq 0)
\end{array}
\right.

import numpy as np
import matplotlib.pylab as plt
def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0,5.0,0.1)
y = relu(x)
plt.plot(x,y)
plt.ylim(-1.0,5.5)
plt.show()

alt

Implementierung eines 3-Schicht-Neuronalen Netzwerks

#Definieren Sie eine Nummer
def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

#Funktion zur Berechnung bis zur Ausgabeebene
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

#Implementierung
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)

Softmax-Funktion

Funktionen, die häufig bei Klassifizierungsproblemen verwendet werden

y_k = \frac{e^{a_k}}{\sum_{i = 1}^{n}e^{a_i}}

Zur Berechnung der Exponentialfunktion sind Überlaufmaßnahmen erforderlich

\begin{align}
y_k & = \frac{Ce^{a_k}}{C\sum_{i = 1}^{n}e^{a_i}} \\
& =  \frac{e^{a_k+\log C}}{\sum_{i = 1}^{n}e^{a_i+\log C}} \\
& =  \frac{e^{a_k+C'}}{\sum_{i = 1}^{n}e^{a_i+C'}} \\
\end{align}

Es ist üblich, den Maximalwert des Eingangssignals für C 'zu verwenden.

import numpy as np
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a/sum_exp_a
    return y

Lernen neuronaler Netze

Lernen = Ermitteln Sie automatisch den optimalen Gewichtsparameterwert aus den Trainingsdaten Führen Sie eine Verlustfunktion ein, damit das neuronale Netzwerk trainieren kann. Ziel: Finden Sie den Gewichtungsparameter, der seinen Wert relativ zur Verlustfunktion minimiert Zu diesem Zweck wird die ** Gradientenmethode ** verwendet.

Datengesteuert

Stellen Sie sich ein Programm vor, das die Nummer "5" erkennt. Es ist sehr schwierig, ein Programm zu erstellen, das "5" von Grund auf erkennt. Nutzen Sie die Daten daher effektiv. Es gibt eine Methode zum Extrahieren von ** Merkmalen ** aus dem Bild und zum Lernen des Musters der Merkmale unter Verwendung der Technologie des maschinellen Lernens. Feature = Konverter zum präzisen Extrahieren wesentlicher Daten (wichtige Daten) aus Eingabedaten (Eingabebild) Im neuronalen Netzwerk lernt die "Maschine" sogar die im Bild enthaltenen Merkmale.

Verlustfunktion

Ein Indikator dafür, wie stark das neuronale Netzwerk nicht mit den Lehrerdaten übereinstimmt (kleiner ist weniger Fehler) Im Allgemeinen gibt es eine Summe aus Quadratfehlern, Kreuzentropiefehlern usw.

Summe der Fehlerquadrate

E = \frac{1}{2}\sum_{k}(y_k - t_k)^2

y _{k </ sub>: Neuronale Netzwerkausgabe
t _{k </ sub>: Lehrerdaten
k: Anzahl der Dimensionen}}

Für Lehrerdaten ist das richtige Antwortetikett 1 und die anderen 0. Diese Methode wird als One-Hot-Notation bezeichnet.

import numpy as np
def mean_squared_error(y,t):
    return 0.5*np.sum((y-t)**2)

Kreuzentropiefehler

E =- \sum_{k}t_k\log y_k

import numpy as np
def cross_entropy_error(y,t):
    delta = 1e-7
    return -np.sum(t*np.log(y + delta))

Durch Hinzufügen einer Minuteneinheit verhindert np.log (0) = -inf, dass die Berechnung unmöglich wird.

Mini-Batch-Lernen

Das Problem des maschinellen Lernens besteht darin, anhand von Trainingsdaten zu lernen → die Verlustfunktion für die Trainingsdaten zu finden und den Wert so klein wie möglich zu halten.

E = - \frac{1}{N}\sum_{n}\sum_{k}{}t_{nk}\log y_{nk}

Es wird normalisiert, indem es auf N Daten erweitert und schließlich durch N dividiert wird. Beim Mini-Batch-Lernen wird nur eine bestimmte Anzahl von Trainingsdaten aus Zehntausenden von Trainingsdaten ausgewählt und für jeden Mini-Batch gelernt.

Steigung

Sammeln der partiellen Differentiale von beiden (x <0> 0 </ sub>, x _{1 </ sub>),}

(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1})

Der Gradient ist die Summe der partiellen Differentiale aller Variablen als Vektor.

import numpy as np
def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx]
        #f(x+h)Berechnung von
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # f(x+h)Berechnung von
        x[idx] = tmp_val + h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2)/(2*h)
        x[idx] = tmp_val #Stellen Sie den Wert wieder her

    return grad

Die Neigung zeigt an jedem Punkt in Absenkrichtung.

Gradientenmethode

Die Gradientenmethode besteht darin, den Gradienten gut zu nutzen und den Minimalwert der Funktion zu finden. Bei der Verlaufsmethode legen Sie eine bestimmte Strecke in Verlaufsrichtung von Ihrem aktuellen Standort zurück, suchen den Verlauf am Ziel und bewegen sich dann wiederholt in Verlaufsrichtung. Reduzieren Sie den Wert der Funktion schrittweise, indem Sie die Verlaufsrichtung wiederholen.

x_0 = x_0 - \eta\frac{\partial f}{\partial x_0} \\
x_1 = x_1 - \eta\frac{\partial f}{\partial x_1}

η stellt die Anzahl der Aktualisierungen dar und wird im neuronalen Netzwerktraining als ** Lernrate ** bezeichnet. Es ist eine Variable, die bestimmt, wie viel in einem Lernen gelernt werden soll und wie viele Parameter aktualisiert werden. Die obige Formel zeigt eine einmalige Aktualisierungsformel, die viele Male wiederholt wird. Der Wert für die Lernrate muss im Voraus festgelegt werden, z. B. 0,01 oder 0,001. Es ist üblich zu überprüfen, ob das Lernen korrekt ist, während der Wert der Lernrate geändert wird.

import numpy as np
def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    for idx in range(x.size):
        tmp_val = x[idx]
        #f(x+h)Berechnung von
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # f(x+h)Berechnung von
        x[idx] = tmp_val + h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2)/(2*h)
        x[idx] = tmp_val #Stellen Sie den Wert wieder her

    return grad

def gradient_descent(f,init_x,lr=0.01,step_num=100):
    x = inti_x

    for i in range(step_num):
        grad = numerical_gradient(f,x)
        x -= lr * grad

    return x

Ich benutze die Funktion, um den Gradienten zu finden. lr repräsentiert die Lernrate und step_num repräsentiert die Anzahl der Iterationen nach der Gradientenmethode.

Gradient in Bezug auf das neuronale Netzwerk

Der Gradient im neuronalen Netzwerk ist der Gradient der Verlustfunktion in Bezug auf den Gewichtsparameter. Wenn das Gewicht W und die Verlustfunktion L ist, ist der Gradient

\frac{\partial L}{\partial W}

Es wird sein.

Lernalgorithmus

Neuronale Netze haben anpassbare Gewichte und Vorurteile, und das Anpassen dieser Gewichte und Vorurteile zur Anpassung an Trainingsdaten wird als "Lernen" bezeichnet. Einige Daten werden zufällig aus den Trainingsdaten ausgewählt. Die ausgewählten Daten werden als Mini-Batch bezeichnet. Der Zweck besteht darin, den Wert der Verlustfunktion des Mini-Batches zu verringern. Ermitteln Sie den Gradienten jedes Gewichtungsparameters, um die Verlustfunktion des Minibatch zu verringern. Der Gradient gibt die Richtung an, in der der Wert der Verlustfunktion am meisten reduziert wird.

<Schritt 3 Parameter aktualisieren> Gewichtsparameter in Gradientenrichtung um einen kleinen Betrag aktualisiert

<Schritt 4 wiederholen> Wiederholen Sie Schritt 1, Schritt 2, Schritt 3

Eine solche Technik wird als ** Probabilistic Gradient Descent (SGD) ** bezeichnet, da zufällig ausgewählte Daten als Mini-Batch verwendet werden.

Zweischichtiges neuronales Netzwerk

Definieren Sie ein zweischichtiges neuronales Netzwerk als eine Klasse.

import sys, os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient

class TwoLayerNet:
    
    #Eingabe initialisieren_Größe ist die Anzahl der Neuronen in der Eingabeebene, die ausgeblendet sind_Größe ist die Anzahl der Neuronen in der verborgenen Schicht, Ausgabe_Größe ist die Anzahl der Neuronen in der Ausgabeschicht
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        #Gewichtsinitialisierung
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)#zufällig
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)#zufällig
        self.params['b2'] = np.zeros(output_size)
        
    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2'] #Ersatzgewichtsparameter
        b1, b2 = self.params['b1'], self.params['b2']#Ersetzen Sie die Bias-Parameter
        
        a1 = np.dot(x, W1) + b1#Berechnung der ersten Schicht x Eingangssignal + Vorspannung
        z1 = sigmoid(a1) #Konvertiere a1, berechnet oben mit Sigmoidfunktion
        a2 = np.dot(z1, W2) + b2 #Gewicht der zweiten Schicht*Berechnung von z1+vorspannen
        y = softmax(a2) #Übergeben Sie a2, das oben berechnet wurde, an y, die Ausgabeebene
        
        return y

    # x:Eingabedaten, t:Lehrerdaten
    def loss(self, x, t):#Verlustfunktion
        y = self.predict(x)#Vorhersage der TwoLayerNet-Klasseninstanz(x)Gibt das Ergebnis von zurück.
        
        return cross_entropy_error(y, t)#Das Ergebnis wird auf den Kreuzentropiefehler angewendet und der Fehler wird durch Vergleich mit den Lehrerdaten berechnet. Zu
    
    #Berechnen Sie die richtige Antwortrate. Erkennungsgenauigkeit
    def accuracy(self, x, t):
        y = predict(x) #predict(x)Ich rechne, aber ich frage mich, ob ich mich nicht brauche?
        y = np.argmax(y, axis=1)#Mit argmax werden nur Etiketten mit hohen Zahlen entfernt.
        t = np.argmax(t, axis=1)#Verwenden Sie argmax, um das richtige Etikett abzurufen.
        
        accuracy = np.sum(y == t)/float(x.shape[0])#y==Wenn t True ist, addieren Sie sie zu 1 und dividieren Sie sie durch die Gesamtzahl der Daten.
        return accuracy
    
    # x:Eingabedaten, t:Lehrerdaten
    #Finden Sie die partielle Differenzierung und den Gradienten
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t) #Lambda anonyme Funktion, Lambda x:y x ist das Argument und y ist der Rückgabewert
        # def loss_W(W):
        #   self.loss(x,t)Sollte die gleiche Bedeutung haben wie.
        
        grads = {}#Absolventen initialisieren.
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])#Gewichtsgradient der ersten Schicht. Berechnet aus der Verlustfunktion und dem Gewicht.
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])#Der Gradient der Vorspannung der ersten Schicht. Berechnet aus der Verlustfunktion und dem Gewicht.
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])#Der Gradient des Gewichts der zweiten Schicht. Berechnet aus der Verlustfunktion und dem Gewicht.
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])#Der Gradient der Vorspannung der zweiten Schicht. Berechnet aus der Verlustfunktion und dem Gewicht.
        
        return grads

[PYTHON] Tiefes Lernen