[PYTHON] Introduction à la modélisation statistique pour l'analyse des données Élargissement de la gamme d'applications de GLM
Nous traitons les travaux à terme décalés de régression logistique et de régression de Poisson, et GLM en utilisant la distribution normale et la distribution gamma.
GLM auquel différents types de données peuvent être appliqués
Différents types de données peuvent être représentés par GLM en combinant des distributions de probabilité, des fonctions de liaison et des prédicteurs linéaires.
Partie de la distribution de probabilité qui peut être utilisée pour construire GLM dans Python
La génération aléatoire est spécifiée par scipy.stats.X, et la famille glm () est spécifiée par statsmodels.api.families.X.
| Distribution de probabilité | Génération aléatoire | glm()Désignation de la famille | Fonctions de lien fréquemment utilisées | |
|---|---|---|---|---|
| (Discret) | Distribution binaire | binom.rvs() | Binomial() | logit |
| Distribution de Poisson | poisson.rvs() | Poisson() | log | |
| Distribution binomiale négative | nbinom.rvs() | NegativeGaussian() | log | |
| (Continu) | Distribution gamma | gamma.rvs() | Ganma() | log? |
| distribution normale | norm.rvs() | Gaussian() | identity |
GLM avec distribution binomiale
La distribution binomiale est utilisée lorsque les données de comptage ont une limite supérieure ** (la variable de réponse est $ y \ in \ {0, 1, 2, \ dots, N \} $).
Lorsque le même traitement a été appliqué aux sujets expérimentaux de N individus, la réaction était positive chez $ y $ individus et négative chez $ N-y $ individus.
Cet exemple est
"Pour chaque $ i $ plante fictive, $ y_i $ graines vivantes et germinables et $ N_i-y_i $ graines mortes sur $ N_i $ graines observées."
Supposons qu'un total de 100 plantes a été étudié en utilisant les données d'observation.
- Le nombre de graines observées $ N_i $ est de 8 pour tout individu.
À propos des variables de réponse
La valeur possible du nombre de graines survivantes, qui est la variable de réponse, est $ y_i \ in \ {0, 1, 2, 3, \ dots, 8 \} $. $ Y_i = 8 $ si tous sont vivants, et $ y_i = 0 $ si tous sont morts.
Soit $ q_i $ la "probabilité qu'une graine obtenue d'un certain individu $ i $ soit vivante".
À propos des variables explicatives
La probabilité de survie $ q_i $ fluctue en fonction de la taille corporelle $ x_i
>>> import pandas
>>> import matplotlib.pyplot as plt
>>> d = pandas.read_csv("data4a.csv")
>>> d.describe()
N y x
count 100 100.000000 100.000000
mean 8 5.080000 9.967200
std 0 2.743882 1.088954
min 8 0.000000 7.660000
25% 8 3.000000 9.337500
50% 8 6.000000 9.965000
75% 8 8.000000 10.770000
max 8 8.000000 12.440000
>>> plt.plot(d.x[d.f == 'C'], d.y[d.f == 'C'], 'bo')
>>> plt.plot(d.x[d.f == 'T'], d.y[d.f == 'T'], 'ro')
>>> plt.show()
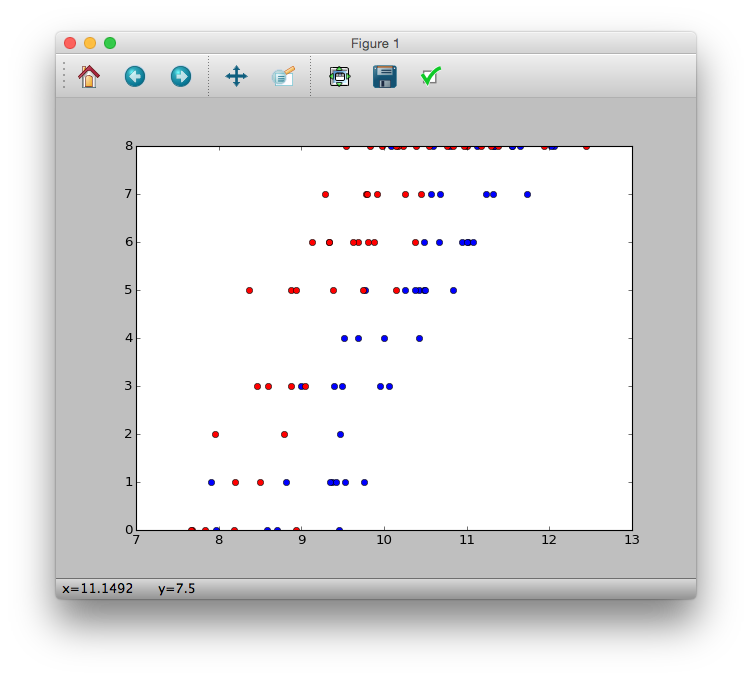
Comme vous pouvez le voir sur la figure
--Il semble que le nombre de graines survivantes $ y_i $ augmente à mesure que la taille du corps $ x_i $ augmente. --Il semble que l'engrais augmentera le nombre de graines survivantes $ y_i $ ($ f_i = T $)
Distribution binaire
p(y|N, q) = \left( \begin{array}{c}
N \\
y
\end{array}
\right) q^y (1-q)^{N-y}
>>> import math
>>> p = lambda y, N, q: (math.factorial(N) / (math.factorial(y) * math.factorial(N-y))) * (q ** y) * ((1-q) ** (N-y))
>>> p1 = [p(i, 8, 0.1) for i in y]
>>> p2 = [p(i, 8, 0.3) for i in y]
>>> p3 = [p(i, 8, 0.8) for i in y]
>>> plt.plot(y, p1, 'b-o')
>>> plt.plot(y, p2, 'r-o')
>>> plt.plot(y, p3, 'g-o')
>>> plt.show()
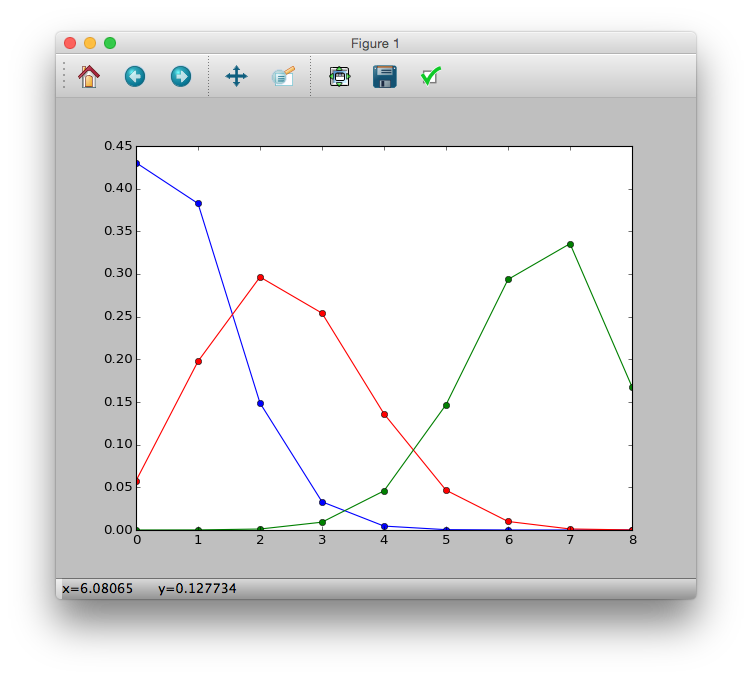
Fonction de régression logistique et de lien logistique
En régression logistique,
- Distribution de probabilité: ** Distribution binaire **
- Fonction de lien: ** fonction de lien logit **
Est utilisé.
À propos de la ** fonction logistique **
q_i = logistic(z_i) = \frac{1}{1+\exp(-z_i)}
La variable $ z_i $ est le prédicteur linéaire $ z_i = \ beta_1 + \ beta_2 x_1 + \ dots $.
>>> logistic = lambda z: 1 / (1 + numpy.exp(-z))
>>> z = numpy.arange(-6, 6, 0.1)
>>> plt.plot(z, logistic(z))
>>> plt.show()

En supposant que la probabilité de survie $ q_i $ est une fonction logistique de $ z_i $, toute valeur du prédicteur linéaire $ z_i $ sera $ 0 \ leq q_i \ leq 1 $.
En supposant que la probabilité de survie $ q_i $ ne dépend que de la taille du corps $ x_i $, le prédicteur linéaire $ z_i = \ beta_1 + \ beta_2 x_i $.
$ Q_i $ et $ x_i $ dépendent de $ \ beta_1 $ et $ \ beta_2 $
>>> plt.subplot(121)
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(0 + 2 * x)))
>>> plt.plot(z, logistic(z), 'b-', label='beta1=0')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(2 + 2 * x)))
>>> plt.plot(z, logistic(z), 'r-', label='beta1=2')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(-3 + 2 * x)))
>>> plt.plot(z, logistic(z), 'g-', label='beta1=-3')
>>> plt.legend(loc='middle right')
>>> plt.subplot(122)
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(2 * x)))
>>> plt.plot(z, logistic(z), 'b-', label='beta2=2')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(4 * x)))
>>> plt.plot(z, logistic(z), 'r-', label='beta2=4')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(-1 * x)))
>>> plt.plot(z, logistic(z), 'g-', label='beta2=-1')
>>> plt.legend(loc='middle right')
>>> plt.show()
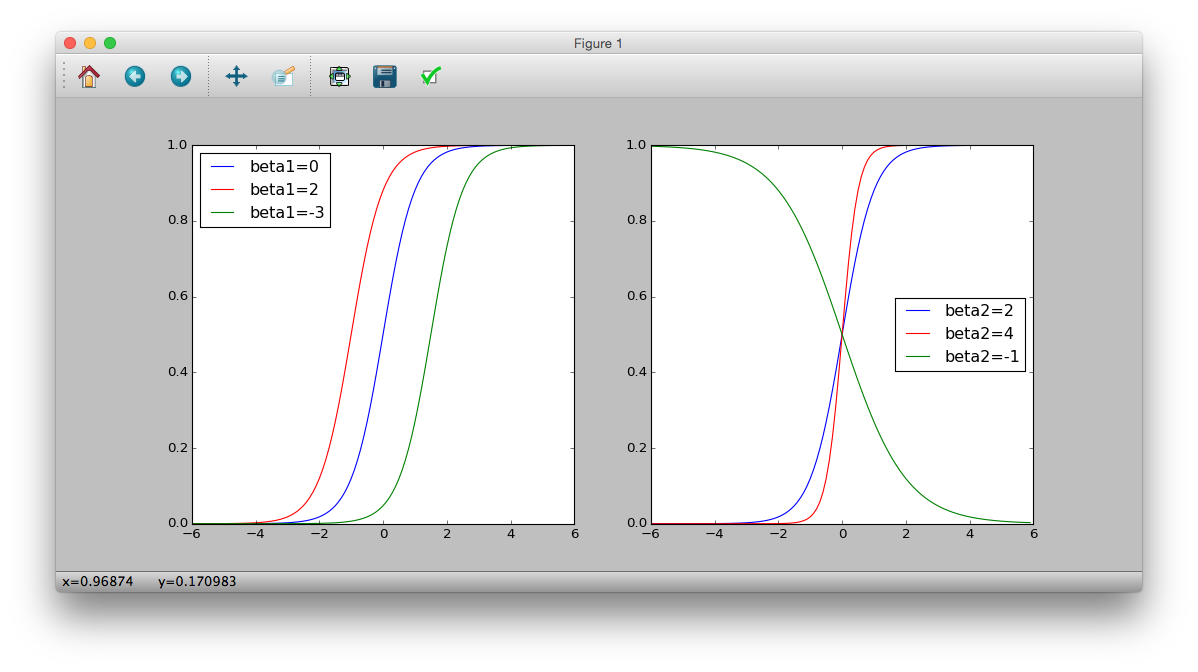
Fonction Logit
Transformez une fonction logistique.
\begin{eqnarray}
q_i &=& \frac{1}{1+\exp(-z_i)} \\
q_i + q_i \exp(-z_i) &=& 1 \\
1 - q_i &=& q_i \exp (-z_i)\\
\frac{1 - q_i}{q_i} &=& \exp (-z_i) \\
\log \frac{1 - q_i}{q_i} &=& -z_i \\
\log \frac{q_i}{1 - q_i} &=& z_i
\end{eqnarray}
Le côté gauche est appelé ** fonction logit **.
logit(q_i) = \log \frac{q_i}{1 - q_i}
- La fonction logit est l'inverse de la fonction logistique.
Estimation des paramètres
Maximisez la probabilité (logique) sous la probabilité de survie $ q_i $.
\begin{eqnarray}
L(q) &=& \prod_i p(y_i | N_i, q_i) \\
&=& \prod_i \left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right)q_i^{y_i}(1-q_i)^{N_i-y_i} \\
L(\{\beta_1, \beta_2, \beta_3\}) &=& \prod_i \left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right)q_i^{y_i}(1-q_i)^{N_i-y_i} (\because logit(q_i) = z_i = \beta_1 + \beta_2 x_i + \beta_3 d_i) \\
logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \log \left\{\left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right)q_i^{y_i}(1-q_i)^{N_i-y_i} \right\} \\
logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \left\{ \log \left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right) + \log q_i^{y_i} + \log (1-q_i)^{N_i-y_i} \right\} \\
logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \left\{ \log \left( \begin{array}{c}
N_i \\
y_i
\end{array}
\right) + (y_i)\log q_i + (N_i-y_i)\log (1-q_i) \right\} \\
\end{eqnarray}
>>> import statsmodels.formula.api as smf
>>> import statsmodels.api as sm
>>> import pandas
>>> d = pandas.read_csv("data4a.csv")
# glm(cbind(y, N-y) ~ x + f, data=d, family=binomial)
>>> model = smf.glm('y + I(N-y) ~ x + f', data=d, family=sm.families.Binomial())
>>> fit = model.fit()
>>> fit.summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: ['y', 'I(N - y)'] No. Observations: 100
Model: GLM Df Residuals: 97
Model Family: Binomial Df Model: 2
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -133.11
Date: Sat, 06 Jun 2015 Deviance: 123.03
Time: 12:06:47 Pearson chi2: 109.
No. Iterations: 8
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -19.5361 1.414 -13.818 0.000 -22.307 -16.765
f[T.T] 2.0215 0.231 8.740 0.000 1.568 2.475
x 1.9524 0.139 14.059 0.000 1.680 2.225
==============================================================================

À propos des cotes
Le rapport (probabilité de survie) / (probabilité de non-survie) est appelé ** cote **.
\begin{eqnarray}
\frac{q_i}{1-q_i} &=& \exp(Prédicteur linéaire) \\
&=& \exp(\beta_1 + \beta_2 x_i + \beta_3 f_i) \\
&=& \exp(\beta_1)\exp(\beta_2 x_i)\exp(\beta_3 f_i)
\end{eqnarray}
Se concentrer sur le $ \ {\ beta_2, \ beta_3 \} $ estimé cette fois
\frac{q_i}{1-q_i} \propto \exp(1.95x_i)\exp(2.02f_i)
Et chaque variable explicative a une relation proportionnelle.
L'effet de la taille du corps $ x_i $ est
\begin{eqnarray}
\frac{q_i}{1-q_i} &\propto& \exp(1.95(x_i + 1))\exp(2.02f_i) \\
&\propto& \exp(1.95x_i)\exp(1.95)\exp(2.02f_i)
\end{eqnarray}
On peut le voir à partir de cette approche $ \ exp (1.95) \ 7,03 $ fois. De même, on peut voir que l'effet de l'application d'engrais est $ exp (2,02) \ approche 7,54 $ fois.
À propos du rapport de cotes
L'effet du facteur $ X $ ($ \ beta_x = 1,95 $) est montré.
\begin{eqnarray}
\frac{Cotes X}{非Cotes X} &=& \frac{\exp(X\bullet Partie commune non-X)\times \exp(1.95 \times 1)}{\exp(X\bullet Partie commune non-X)\times \exp(1.95 \times 0)} \\
&=& exp(1.95) \approx 7.03
\end{eqnarray}
Sélection de modèle
Sélection du modèle par AIC Sélection de modèles imbriqués pour la régression logistique
--Modèle constant (section uniquement) --x modèle (taille du corps uniquement) --f modèle (effet de fécondation uniquement)
- Modèle x + f (taille du corps + effet d'application d'engrais)
Il semble que R ait une fonction stepAIC () du paquet MASS.
Pour le moment, s'il est identique à la fois précédente, le modèle x + f a l'AIC le plus bas et est un bon modèle.
Terme d'interaction
Considérez l'effet de la multiplication de la taille corporelle et l'effet de l'application d'engrais. En d'autres termes
logit(q_i) = \beta_1 + \beta_2 x_i + \beta_3 f_i + \beta_4 x_i f_i
penser à.
# glm(cbind(y, N-y) ~ x * f, data=d, family=binomial)
>>> model = smf.glm('y + I(N-y) ~ x * f', data=d, family=sm.families.Binomial())
>>> model.fit().summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: ['y', 'I(N - y)'] No. Observations: 100
Model: GLM Df Residuals: 96
Model Family: Binomial Df Model: 3
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -132.81
Date:sol, 06 6 2015 Deviance: 122.43
Time: 13:44:31 Pearson chi2: 13.6
No. Iterations: 8
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -18.5233 5.335 -3.472 0.001 -28.979 -8.067
f[T.T] -0.0638 7.647 -0.008 0.993 -15.052 14.924
x 1.8525 0.525 3.529 0.000 0.824 2.881
x:f[T.T] 0.2163 0.792 0.273 0.785 -1.336 1.769
==============================================================================
Et cette fois, l'AIC a augmenté, donc il n'y a pas eu d'interaction.
Arrêter la modélisation statistique des valeurs de division
L'un des avantages de la régression logistique est qu'il n'est pas nécessaire de créer une valeur de division de $ (données d'observation) / (données d'observation) $. L'endroit de division a tendance à être créé lorsque vous voulez savoir "de quoi dépend la probabilité de survie des graines" dans cet exemple.
Comme un inconvénient
- ** Les informations sont perdues **: taux de frappeur de baseball à titre d'exemple. 300 coups en 1000 coups et 30 coups en 100 coups sont tous deux des frappeurs à 30%, mais peut-on dire qu'ils sont tout aussi certains?
- ** Quelle est la distribution des valeurs converties? **: Quel type de distribution de probabilité suit la valeur de division créée par les quantités comportant des erreurs?
Travail à terme décalé qui ne nécessite pas de valeur de division
Utilisez des données fictives telles que
--Définissez 100 sites d'enquête autour de la forêt ($ i \ in \ {1, 2, \ dots, 100 \} $) --La zone $ A_i $ est différente pour chaque site d'enquête $ i $ --Mesure de la "luminosité" $ x_i $ du site d'enquête $ i $
- Enregistré le nombre d'individus végétaux $ y_i $ sur le site d'enquête $ i $
- (Objectif de l'analyse) Je voudrais savoir comment la "densité de population" des plantes individuelles sur le site d'étude $ i $ est affectée par la "luminosité" $ x_i $.
La densité de population au site d'enquête $ i $, qui a une superficie de $ A_i $, est
\frac{Nombre moyen d'individus\lambda_i}{A_i} =Densité de population
Est. La densité de population est une quantité positive, alors combinez la fonction exponentielle avec la dépendance de luminosité $ x_i $,
\begin{eqnarray}
\lambda_i &=& A_i \multiplié par la densité de population\\
&=& A_i \exp(\beta_1 + \beta_2 x_i) \\
&=& \exp(\beta_1 + \beta_2 x_i + \log A_i)
\end{eqnarray}
Par conséquent, il devient un GLM de distribution de Poisson de fonction de lien logarithmique avec $ z_i = \ beta_1 + \ beta_2 x_i + \ log A_i $ comme prédicteur linéaire.
>>> d = pandas.read_csv("data4b.csv")
>>> model = smf.glm('y ~ x', offset=numpy.log(d.A), data=d, family=sm.families.Poisson())
>>> model.fit().summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -323.17
Date: Sat, 06 Jun 2015 Deviance: 81.608
Time: 14:45:24 Pearson chi2: 81.5
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 0.9731 0.045 21.600 0.000 0.885 1.061
x 1.0383 0.078 13.364 0.000 0.886 1.191
==============================================================================
Distribution normale et sa probabilité
Distribution de probabilité pour la gestion des données de valeur continue dans un modèle statistique. Elle est également appelée ** distribution gaussienne **.
Les paramètres sont
--Valeur moyenne $ \ mu $: peut être modifiée librement dans la plage $ \ pm \ infty $.
- Déviation standard $ \ sigma $: la variation des données peut être spécifiée.
p(y| \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp \left\{ -\frac{(y-\mu)^2}{2\sigma^2} \right\}
# y <- seq(-5, 5, 0.1)
# plot(y, dnorm(y, mean=0, sd=1), type="l")
plt.subplot(131)
plt.plot(y, sct.norm.pdf(y, loc=0, scale=1))
plt.title('$\mu=0, \sigma=1$')
plt.subplot(132)
plt.plot(y, sct.norm.pdf(y, loc=0, scale=3))
plt.title('$\mu=0, \sigma=3$')
plt.subplot(133)
plt.plot(y, sct.norm.pdf(y, loc=2, scale=1))
plt.title('$\mu=2, \sigma=1$')
plt.show()
Dans R, $ \ mu $ est
meanet $ \ sigma $ estsd. En python, $ \ mu $ estlocet $ \ sigma $ estscale.

Paramètres ajustés pour chacun. L'axe vertical montre la ** densité de probabilité **. La zone peinte en rouge est représentée par la magnitude de la probabilité de devenir $ 1,2 \ leq y \ leq 1,8 $.
Si la fonction de densité de probabilité de la distribution normale est $ p (y | \ mu, \ sigma) $
$p(1.2 \leq y \leq 1.8| \mu, \sigma) = \int_{1.2}^{1.8}p(y| \mu, \sigma)dy
#Distribution cumulative
# pnorm(1.8, 0, 1) - pnorm(1.2, 0, 1)
>>> sct.norm.cdf(1.8, 0, 1) - sct.norm.cdf(1.2, 0, 1)
0.079139351108782452
Puisque la probabilité est la zone, elle est approximée comme un rectangle. Dans ce cas, si la hauteur est $ p (y = 1,5 | 0, 1) $ et la largeur est $ \ Delta y = 1,8-1,2 = 0,6 $,
#Densité de probabilité
# dnorm(1.5, 0, 1) * 0.6
>>> sct.norm.pdf(1.5, 0, 1) * 0.6
0.077710557399535043
On voit que l'approximation est faite.
Estimation la plus probable
$ Probability = Basé sur la fonction de densité de probabilité \ times \ Delta y $.
Soit $ {\ bf Y} = \ {y_i \} $ les données de hauteur d'un groupe humain de $ N $ personnes. La probabilité qu'un $ y_i $ soit $ y_i-0,5 \ Delta y \ leq y_i \ leq y_i + 0,5 \ Delta y $ est la fonction de densité de probabilité $ p (y_i | 0, 1) $ et la largeur de l'intervalle $ \ Delta y $. Parce qu'il peut être considéré comme un siège de La fonction de vraisemblance (logique) d'un modèle statistique utilisant une distribution normale est.
\begin{eqnarray}
L(\mu, \sigma) &=& \prod_i p(y_i|\mu, \sigma)\times \Delta y \\
&=& \prod_i \frac{1}{\sqrt{2\pi\sigma^2}}\exp \left\{ -\frac{(y-\mu)^2}{2\sigma^2}\right\} \Delta y \\
log L(\mu, \sigma) &=& \sum_i \left\{-\log \sqrt{2\pi\sigma^2} + \log \Delta y - \frac{(y-\mu)^2}{2\sigma^2} \right\} \\
&=& -0.5N\log(2\pi\sigma^2) + N\log \Delta y - \frac{1}{2\sigma^2}\sum_i (y-\mu)^2
\end{eqnarray}
Il devient. Notez que $ \ Delta y $ est une constante et n'affecte pas le paramètre $ \ {\ mu, \ sigma \} $. Ignorez l'équation ci-dessus. Donc,
log L(\mu, \sigma) = -0.5N\log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_i (y-\mu)^2
Il devient.
GLM avec distribution gamma
** La distribution gamma ** est une distribution de probabilité continue dans laquelle la plage de variables de probabilité est égale ou supérieure à 0. La fonction de densité de probabilité est.
p(y|s, r) = \frac{r^s}{\Gamma(s)}y^{s-1}\exp(-ry)
$ s $ est le paramètre de forme, $ r $ est le paramètre de taux, $ \ frac {1} {r} $ est appelé le paramètre d'échelle et $ \ Gamma (s) $ est la fonction gamma. La moyenne est $ \ frac {s} {r} $ et la variance est $ \ frac {s} {r ^ 2} $. De plus, lorsque $ s = 1 $, la ** distribution exponentielle ** est obtenue.
# dgamma(y, shape, rate)
# 1/rate = scale
>>> y = numpy.arange(0, 5, 0.05)
>>> plt.subplot(131)
>>> plt.plot(y, sct.gamma.pdf(y, a=1, scale=1))
>>> plt.title('$s=1, scale=1/r=1$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=1, scale=1), color='r')
>>> plt.subplot(132)
>>> plt.plot(y, sct.gamma.pdf(y, a=5, scale=0.2))
>>> plt.title('$s=5, scale=1/r=1/5=0.2$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=5, scale=0.2), color='r')
>>> plt.subplot(133)
>>> plt.plot(y, sct.gamma.pdf(y, a=0.1, scale=10))
>>> plt.title('$s=0.1, scale=1/r=1/0.1=10$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=0.1, scale=10), color='r')
>>> plt.show()
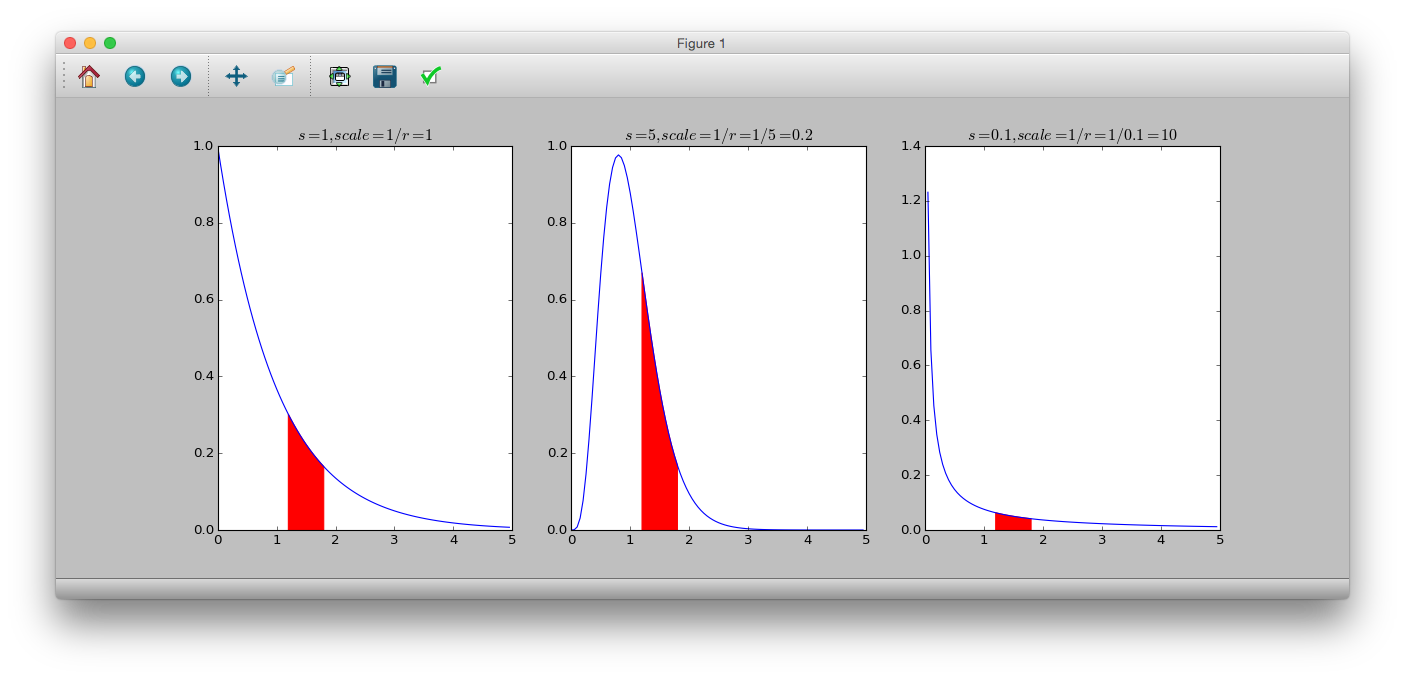
Exemple: Relation entre le poids des feuilles et le poids des fleurs d'une plante fictive
Il semble qu'à mesure que $ x_i $ grandit, il en va de même pour $ y_i $.
\begin{eqnarray}
\mu_i &=& Ax_i^b \\
&=&\exp(a)x_i^b = \exp(a+b\log x_i) (\because A = \exp(a)) \\
\log\mu_i &=& a+blogx_i
\end{eqnarray}
>>> model = smf.glm('y ~ numpy.log(x)', data=d, family=sm.families.Gamma(link=sm.families.links.log))
>>> model.fit().summary()
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 50
Model: GLM Df Residuals: 48
Model Family: Gamma Df Model: 1
Link Function: log Scale: 0.325084605974
Method: IRLS Log-Likelihood: 58.471
Date: Sat, 06 Jun 2015 Deviance: 17.251
Time: 20:38:39 Pearson chi2: 15.6
No. Iterations: 12
================================================================================
coef std err z P>|z| [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Intercept -1.0403 0.119 -8.759 0.000 -1.273 -0.808
numpy.log(x) 0.6832 0.068 9.992 0.000 0.549 0.817
================================================================================
get_y_mean = lambda b1, b2, x: numpy.exp(b1 + b2 * numpy.log(x))
model = smf.glm('y ~ numpy.log(x)', data=d, family=sm.families.Gamma(link=sm.families.links.log))
vc = model.fit().params
ax = plt.figure().add_subplot(111)
ax.plot(d.x, d.y, 'o')
ax.plot(d.x, get_y_mean(-1, 0.7, d.x),'--')
ax.plot(d.x, get_y_mean(vc[0], vc[1], d.x))
phi = model.fit().scale
m = get_y_mean(vc[0], vc[1], d.x)
scale = [(i * phi) for i in m]
shape = 1 / phi
def plot_pi(q):
x = numpy.r_[numpy.array(d.x), numpy.array(d.x)[::-1]]
y = numpy.r_[sct.gamma.ppf(q, a=shape, scale=scale), sct.gamma.ppf(1-q, a=shape, scale=scale)[::-1]]
pair = [(x[i], y[i]) for i in range(len(x))]
poly = plt.Polygon(pair, alpha=0.2, edgecolor='none')
return poly
ax.add_patch(plot_pi(0.05))
ax.add_patch(plot_pi(0.25))
plt.show()

Recommended Posts