[PYTHON] Lernen Sie die M-H- und HMC-Methoden, indem Sie die Bayes'schen Statistiken anhand der Grundlagen lesen
Einführung (warum hast du das gewählt)
Die Stichprobe ist eine der Methoden, die in Situationen angewendet werden, in denen die Integralberechnung schwierig ist, aber ich habe die Stichprobenmethode lange nicht verstanden (zum Beispiel verstehe ich PRML §11 ┐ (´ ー `) ┌ nicht ). In letzter Zeit habe ich jedoch manchmal Artikel gelesen, in denen Stichprobenverfahren verwendet wurden, und deshalb habe ich mich entschlossen, die Grundlagen zu studieren.
Vor kurzem, als er von einem Zug im Viehgeschäft des Unternehmens erschüttert wurde
Da ich das Buch gelesen habe, möchte ich die M-H-Probenahme und die HMC-Methode zusammenfassen, die in den Kapiteln 4 und 5 aufgeführt sind. Der Inhalt entspricht fast dem Beispiel im Buch. Ich wollte unbedingt zu Anhang B für Slice Sampling und NUTS gehen, aber meine Arbeit explodierte und ich hatte nicht genug Zeit (ich werde später mehr tun).
Nachdem ich den folgenden Code organisiert habe, lade ich ihn auf Github oder Bitbucket hoch.
Beispiel
Die Poisson-Verteilung wird als Wahrscheinlichkeitsverteilung seltener Ereignisse verwendet, und die Gamma-Verteilung wird als vorherige Verteilung verwendet. Da es sich bei der Gammaverteilung um eine konjugierte vorherige Verteilung der Poisson-Verteilung handelt, ist eine Abtastung zunächst nicht erforderlich, wird jedoch als Beispiel verwendet (§3 in diesem Buch).
Abbildung der Poisson-Verteilung
sample.py
import numpy as np
import scipy.stats as sst
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
###Poisson-Verteilung (Mittelwert 2.5)Beispiel
from scipy.stats import poisson
mu = 2.5
x = np.arange(poisson.ppf(0.01, mu), poisson.ppf(0.99, mu))
plt.plot(x, poisson.pmf(x, mu), 'bo', ms=8, label='poisson pml')
plt.vlines(x, 0, poisson.pmf(x, mu), colors='b', lw=5, alpha=0.5)

Einführung der Gammaverteilung als vorherige Verteilung und Berechnung der posterioren Verteilung
Die posteriore Verteilung wird unter der Annahme berechnet, dass die Daten (0, 1, 0, 0, 2, 0, 1, 0, 0, 1), die die Poisson-Verteilung zu sein scheinen, angemessen beobachtet werden. Wie ich oben geschrieben habe, kann die Form der posterioren Verteilung verstanden werden, da es sich in erster Linie um eine konjugierte vorherige Verteilung handelt.
sample.py
#Daten
x_data = np.array([0, 1, 0, 0, 2, 0, 1, 0, 0, 1])
#Vorherige Verteilung (Gammaverteilung mit einem Durchschnitt von 2))
f_prev = gamma(a=6.0, scale=1.0/3.0)
x = np.linspace(0.0, 5.0, 100)
plt.plot(x, f_prev.pdf(x), 'b-', label='Prev')
#Ex-post-Verteilung
n = x_data.shape[0]
ap = np.sum(x_data)
print("observe {0} positive {1}".format(n, ap))
f_post = gamma(a=6.0+ap, scale=1.0/(3.0 + n))
plt.plot(x, f_post.pdf(x), 'r--', label='Post')
plt.legend()

Probenahme nach der Metropolis-Hastings-Methode
Der Parameter sei $ \ theta $. Für den aktuellen Wert $ \ theta ^ {(t)} $ und den Wert $ \ theta_a $, der aus der vorgeschlagenen Verteilung entnommen wurde, wird wahrscheinlich bestimmt, ob $ \ theta_a $ erforderlich ist.
Im Fall der Poisson-Verteilung und der Gamma-Verteilung dieses Mal ist die posteriore Verteilung, die wir finden möchten, proportional zum Produkt der Wahrscheinlichkeit und der vorherigen Verteilung (Gamma-Verteilung mit den Parametern α = 11, λ = 13 im Beispiel) gemäß dem Bayes'schen Gesetz, also $ r $ Durch Transformation der Formel von
sample.py
#Daten
x_data = np.array([0, 1, 0, 0, 2, 0, 1, 0, 0, 1])
#Haftung
def log_likelihood(x, theta):
x_probs = poisson.pmf(x, theta)
return np.sum(np.log(x_probs))
#Gamma-Verteilungskern
def k_fg(theta, a, lbd): return np.exp(-lbd * theta) * (theta ** (a-1))
#Vorgeschlagene Verteilung;Durchschnittliches Theta,Standardabweichung 0.Normalverteilung von 5
def q(x, theta): return sst.norm.pdf(x, loc=theta, scale=0.5)
# M-H-Schleife (Anfangswert 1.0, 1000 mal)
def metropolis_raw(N):
current = 1.0 #Ursprünglicher Wert
sample = []
sample.append(current)
for iter in range(N):
a = sst.norm.rvs(loc=prop_m, scale=prop_sd)
if a < 0: # reject (In der vorgeschlagenen Verteilung
sample.append(sample[-1])
continue
T_next = q(current, a) * k_fg(a, a=11.0, lbd=13.0) * log_likelihood(x_data, a)
T_prev = q(a, current) * k_fg(current, a=11.0, lbd=13.0) * log_likelihood(x_data, current)
ratio = T_next / T_prev
if ratio < 0: # reject
sample.append(sample[-1])
if ratio > 1 or ratio > sst.uniform.rvs():
sample.append(a)
current = a
else:
sample.append(sample[-1])
return np.array(sample)
N = 10000
theta = metropolis_raw(N)
n_burn_in = 1000
# theta trace
plt.figure(figsize=(10, 3))
plt.xlim(0, len(theta)-n_burn_in)
plt.title("Trace plot from M-H sampling. burn-in:{}".format(n_burn_in))
plt.plot(theta[n_burn_in:], alpha=0.9, lw=.3)
# plot samples
plt.figure(figsize=(5,5))
plt.title("Histgram from M-H sampling.")
plt.hist(theta[n_burn_in:], bins=50, normed=True, histtype='stepfilled', alpha=0.2)
xx = np.linspace(0, 2.5,501)
plt.plot(xx, sst.gamma(11.0, 0.0, 1/13.).pdf(xx))
plt.show()
Ist die Implementierung falsch, überraschend nicht gut


Unabhängige M-H-Methode
Im obigen Beispiel wurde die Normalverteilung (vorgegebene Parameter) als vorgeschlagene Verteilung verwendet, aber ist es nicht in Ordnung, wenn f und q überhaupt unabhängig sind? → Unabhängige M-H-Methode
sample.py
import scipy.stats as sst
#Vorgeschlagene Verteilung;Normalverteilung(Feste Parameter)
prop_m, prop_sd = 1.0, 0.5
def q(x): return sst.norm.pdf(x, loc=prop_m, scale=prop_sd)
#Ersetzen Sie die Berechnung von a und r
a = sst.norm.rvs(loc=prop_m, scale=prop_sd)
r = (q(current)*k_fg(a,a=11.0, lbd=13.0)) / (q(a)*k_fg(current,a=11.0,lbd=13.0))


Ich mache mir Sorgen um die Implementierung.
Random-Walk-M-H-Methode
Lassen Sie uns zufällig die Kandidatenpunkte gehen (gerader Ball) → Wenn eine Normalverteilung verwendet wird, werden der vorgeschlagene Wert (a) und die bisherige Varianz angemessen in den Durchschnitt einbezogen.
sample.py
current = 4.0
list_theta = []
list_theta.append(current)
#Für zufälliges Gehen (verwischen Sie die angegebenen Parameter im Durchschnitt)
def f_g(theta):
prop_sd = np.sqrt(0.1)
return sst.norm.rvs(loc=theta, scale=prop_sd)
###Ersetzen Sie den berechneten Teil von a und r
a = f_g(current)
r = f_gamma(a) / f_gamma(current)


Es ist etwas besser, wenn Sie die Anzahl der Wiederholungen erhöhen.
Bonus (Scipy-Funktion)
Die Stichprobenfähigkeit der Kopffamilie.
sample.py
import scipy.stats as sst
lbd = 1.0/13
plt.rcParams["figure.figsize"] = [4, 4]
a = 11.0
rv = sst.gamma(a, scale=lbd)
x = np.linspace(sst.gamma.ppf(0.01, a, scale=lbd), sst.gamma.ppf(0.99, a, scale=lbd), 100)
plt.plot(x, rv.pdf(x), 'r-', lw=5, alpha=0.6, label='gamma pdf')
plt.plot(x, rv.pdf(x), 'k-', lw=2, label='frozen pdf')
vals = rv.ppf([0.001, 0.5, 0.999])
np.allclose([0.001, 0.5, 0.999], sst.gamma.cdf(vals, a, scale=lbd))
r = sst.gamma.rvs(a, scale=lbd,size=9000)
plt.hist(r, normed=True, bins=100, histtype='stepfilled', alpha=0.2)
plt.legend(loc='best', frameon=False)

HMC-Methode
In der Physik der High School habe ich gelernt, dass mechanische Energie (kinetische Energie + Positionsenergie) erhalten bleibt, wenn keine äußere Kraft angewendet wird (kein anderer Verlust durch Licht oder Wärme). Es sollten viele Leute sein. In der analytischen Mechanik wird dies als Hamilton-Operator gelesen und in verallgemeinerten Koordinaten diskutiert. Wie es beiseite gelegt wird (wahrscheinlich früher geschrieben, wenn Sie ein geeignetes analytisches Mechanikbuch öffnen)
Ich überlasse die Details dem Buch, setze die logarithmische posteriore Verteilung auf $ -h (\ theta) $, berechne den Hamilton-Operator als $ h (x) + \ frac {1} {2} p ^ 2 $ und folge den folgenden Schritten. Die HMC-Methode ist die Methode der Probenahme mit (im Fall einer Dimension).
- [Leaf Frog Method](https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%BC%E3%83%97%E3%83%BB%E3%83%95 % E3% 83% AD% E3% 83% 83% E3% 82% B0% E6% B3% 95) Bestimmen Sie $ \ epsilon, L, T $ als Parameter von.
- Bestimmen Sie den Anfangswert $ \ theta ^ {(0)} $ und setzen Sie $ i = 0 $ (wiederholen Sie 3 bis 6 bis zum angegebenen $ i $).
- Stichprobe aus der Standardnormalverteilung… $ p ^ {(i)} \ sim \ mathcal {N} (p ^ {(i)} \ mid 0, 1) $
- Ändern Sie $ \ theta ^ {(i)} $ und $ p ^ {(i)} $ um L Schritte nach der Sprungfroschmethode und ändern Sie die Kandidatenpunkte $ \ theta ^ {(a)}, p ^ {(a) } $
- $ r = \ exp \ (H (\ theta ^ {(t)}, p ^ {(t)}) - H (\ theta ^ {(a)}, p ^ {(a)}) ) Akzeptieren Sie als $ 5 Assistant Stores mit einer Wahrscheinlichkeit von $ \ min (1, r) $ und verwerfen Sie sie anderweitig.
- t = t+1
Lassen Sie es uns implementieren und sehen, wie es funktioniert. Poisson-Verteilung-Gamma-Verteilungsmodell mit posteriorer Verteilung ohne Normalisierungskonstanten
hmc_sample.py
#Definition der Differenzierung von h und h
alpha, lbd = 11, 13
def _h(theta, alpha, lbd):
return lbd * theta - (alpha - 1) * np.ma.log(theta)
def _hp(theta, alpha, lbd):
return lbd - (alpha - 1) / theta
h = lambda theta: _h(theta, alpha, lbd)
hp = lambda theta: _hp(theta, alpha, lbd)
###Hamiltonianer
def H(theta, p):
return h(theta) + 0.5 * p * p
###Einfache Implementierung der Sprungfroschmethode
def lf(_th, _p, epsilon, L):
l_p = [_p]
l_th = [_th]
for tau in range(1, L):
p_t = l_p[-1]
theta_t = l_th[-1]
# 1/2
p_t_half = p_t - 0.5 * epsilon * hp(theta_t)
# update
next_theta = theta_t + epsilon * p_t_half
next_p = p_t_half - 0.5 * epsilon * hp(next_theta)
# store
l_p.append(next_p)
l_th.append(next_theta)
return (l_th[-1], l_p[-1])
###HMC-Probenahme
N = 10000
moves = []
theta = [2.5]
p = []
L = 100
epsilon = 0.01
for itr in range(N):
pv = sst.norm.rvs(loc=0, scale=1, size=1)[0]
p.append(pv)
# candidate by LF
curr_th, curr_p = theta[itr], p[itr]
cand_th, cand_p = lf(curr_th, curr_p, epsilon, L)
# compute r by exp(H(curr) - H(cand))
Hcurr = H(curr_th, curr_p)
Hcand = H(cand_th, cand_p)
r = np.exp(Hcurr - Hcand)
# print("{0}\t{1:2.4f}\t{2:2.4f}".format(itr, cand_th, cand_p))
# print("\t\t\t{0:2.3f}\t{1:2.3f}\t{2:2.3f}".format(Hcurr, Hcand, r))
if r < 0:
#reject
theta.append(theta[-1])
p.append(p[-1])
continue
if r >= 1 or r > sst.uniform.rvs():
theta.append(cand_th)
p.append(cand_p)
moves.append( (curr_th, cand_th, curr_p, cand_p) )
curr_th, curr_p = cand_th, cand_p
else:
#Reject
theta.append(theta[-1])
Trace- und Histogramm-Diagramme.


Gute Stimmung.
Konturlinien zeichnen
hmc_sample.py
lin_p = np.linspace(-6.5, 6.5, 100.0)
lin_theta = np.linspace(0.01, 3.51, 100.0)
X, Y = np.meshgrid(lin_theta, lin_p)
Z = H(X, Y)
# 1dim h(theta)
xx = np.linspace(0.01, 3.01, 100)
plt.figure(figsize=(14, 7))
plt.title("h")
plt.plot(xx, h(xx), lw='1.5', alpha=0.8, color='r')
plt.xlim(-0.1, 3.5)
plt.xlabel("theta")
plt.ylabel("h(theta)")
# 2dim
plt.figure(figsize=(14,7))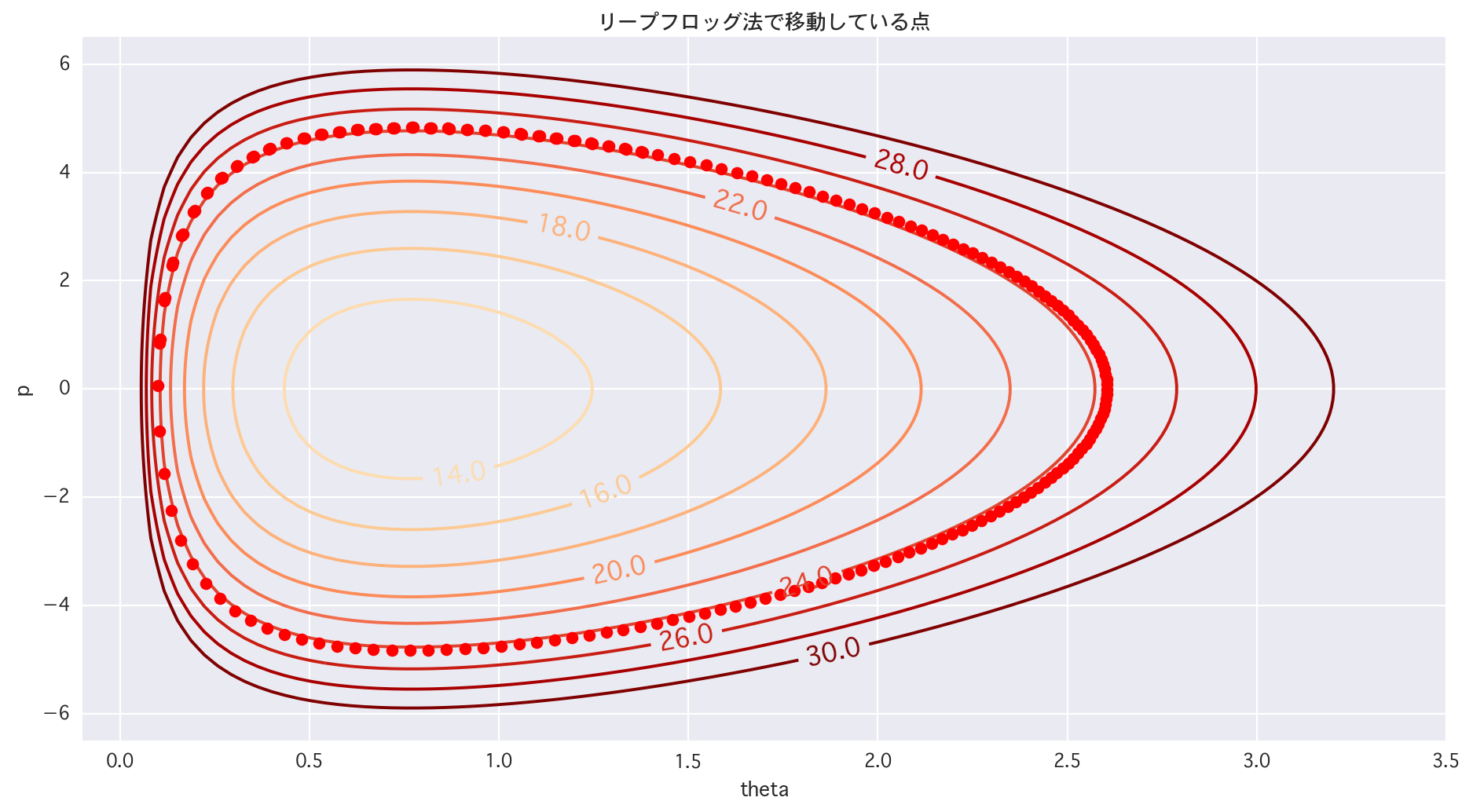
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
plt.xlim(-0.1, 3.5); plt.ylim(-6.5, 6.5); plt.xlabel("theta"); plt.ylabel("p"); plt.show()


hmc_smaple.py
# 2dim (trace of LF)
# 1/4 Bereiche
plt.figure(figsize=(14,7))
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
for tau in range(1, len(p)):
plt.plot(theta[tau], p[tau], 'ro')
plt.title(u"Der Bewegungspunkt nach der Sprungfroschmethode")
plt.xlim(-0.1, 3.5)
plt.ylim(-6.5, 6.5)
plt.xlabel("theta")
plt.ylabel("p")
plt.show()
Ich fühle den Wunsch, Hamiltonian zu retten (angemessen)

hmc_sample.py
#Von welchem Punkt zu welchem Punkt
# 1/4 Bereiche
plt.figure(figsize=(14,7))
cont = plt.contour(X, Y, Z, levels=[i for i in range(10, 32, 2)], cmap="OrRd")
cont.clabel(fmt='%2.1f', fontsize=14)
# for tau in range(1, len(p)):
# plt.plot(theta[tau], p[tau], 'ro')
plt.title(u"Der Bewegungspunkt nach der Sprungfroschmethode")
plt.xlim(-0.1, 3.5)
plt.ylim(-6.5, 6.5)
plt.xlabel("theta")
plt.ylabel("p")
for i in range(len(moves)):
t0, t1, p0, p1 = moves[i][0], moves[i][1], moves[i][2], moves[i][3]
# plt.plot([t0, t1], [p0, p1], 'r-')
plt.plot([t0, t1], [p0, p1], 'r-')
plt.plot(t0, p0, 'ro')
plt.plot(t1, p1, 'bo')
plt.show()

Es wird gelernt, wann man es tatsächlich bewegt.
Pläne
Was ich zurückgelassen habe, wird später in diesem Jahr verdaut und aktualisiert (Flagge)
- Slice Sampling
- NUTS
Recommended Posts