Simulieren wir den Übergang der Infektionsrate in Bezug auf die Bevölkerungsdichte mit Python
Discramer
Ich bin weder ein Experte für Infektionswissenschaften oder Immunologie noch ein Experte für Zellautomaten, daher sind die Formulierungen und Prämissennummern wahnsinnig angemessen. Bitte entschuldigen Sie. Bitte sehen Sie es als Teil des Materials zu mathematischen Modellen und Python-Programmierung.
Motivation
** Es wird gesagt, dass der Kontakt um 80% reduziert wird, aber sollte er um 70% reduziert werden? ** Oder ** Wie lange dauert die Konvergenz? Um diese Zeit gibt es einige Stimmen, die ** sagen. Natürlich werden die genauen Zahlen täglich durch PCR-Tests usw. bestätigt. Wenn Sie jedoch grob abschätzen möchten, wie sich die Anzahl der Infizierten ausbreitet, kommt ein mathematisches Modell ins Spiel. Erstellen wir also ein einfaches ** Spielzeugmodell ** und simulieren den Übergang der Anzahl infizierter Personen in der gesamten Bevölkerung in Bezug auf eine bestimmte Bevölkerungsdichte, die Wahrscheinlichkeit einer Infektion bei engem Kontakt und die Heilungsrate. Es war. * Da es sich um ein Spielzeugmodell handelt, ist es Unsinn, die Richtlinie damit zu diskutieren. Es scheint hartnäckig zu sein, aber bitte sehen Sie es zum Zweck der intellektuellen Neugier. </ font>
Mathematisches Modell
Der Einfachheit halber gehen wir von folgenden Annahmen aus.
-
Bewohner einer flachen zweidimensionalen Welt ohne Meer oder Berge (kurz ** Zellautomat **).

-
Jeder geht zu Fuß und benutzt weder Shinkansen noch Flugzeug (die maximale Fahrstrecke für einen Zeitpunkt beträgt 1, und es gibt auch diagonale Bewegungen).

-
Menschen mit engem Kontakt (benachbarte Zellen) haben eine 20% ige Chance, am nächsten Tag infiziert zu werden.
 Mit anderen Worten, ** die Annahme, dass sich die Anzahl der infizierten Personen in einem Cluster mit engem Kontakt in 4 Tagen verdoppeln wird **.
Mit anderen Worten, ** die Annahme, dass sich die Anzahl der infizierten Personen in einem Cluster mit engem Kontakt in 4 Tagen verdoppeln wird **.
(1+0.20)^4 = 2.07... \approx 2
- Eine infizierte Person hat eine 2% ige Chance, am nächsten Tag geheilt zu werden.
 Mit anderen Worten, ** die Annahme, dass etwa die Hälfte der infizierten Menschen in einem Monat (31 Tagen) heilen wird **.
Mit anderen Worten, ** die Annahme, dass etwa die Hälfte der infizierten Menschen in einem Monat (31 Tagen) heilen wird **.
1-(1-0.02)^{31} = 0.46... \approx 0.5
Ich habe es tatsächlich geschafft.
Die Anzahl der infizierten Personen zum Zeitpunkt t = 0 (Tag) beträgt 5% der Gesamtzahl (5 von 100 Personen sind zuerst infiziert).
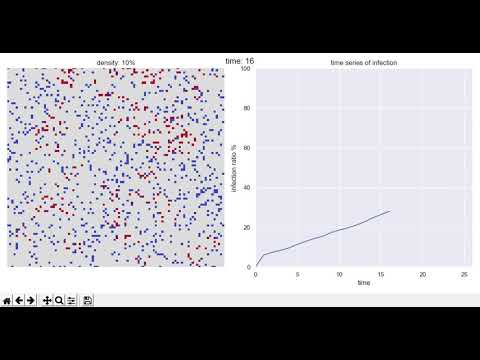
Die Abbildung links zeigt den Status der Gruppe ein Jahr (365 Tage) nach dem Start: Blau ist gesunde Menschen </ font>, Rot ist Wenn Sie eine infizierte Person sind und es insgesamt hellrot ist, ist es wie eine Pandemie </ font>.
Die Abbildung rechts zeigt den Zeitreihenübergang der Infektionsrate. Die horizontale Achse ist die Zeit und die vertikale Achse ist die Infektionsrate. Der Punkt ist dies ↓.

Bevölkerungsdichte = 10% Fall (Großstadt)
Dies ist ein Fall, in dem 10 Personen in 100 Zellen leben. Wie Sie der Abbildung entnehmen können, handelt es sich um ein Bild einer Großstadt.
 Nach einem Jahr befand sich die Gruppe in einem leuchtend roten Pandemiezustand.
Aufgrund der Logik der natürlichen Heilung erreicht die Infektionsrate nicht 100% und ist mit etwa 90% gesättigt, es wird jedoch keine Konvergenz erwartet.
Nach einem Jahr befand sich die Gruppe in einem leuchtend roten Pandemiezustand.
Aufgrund der Logik der natürlichen Heilung erreicht die Infektionsrate nicht 100% und ist mit etwa 90% gesättigt, es wird jedoch keine Konvergenz erwartet.
Fall der Bevölkerungsdichte = 4% (60% weniger Kontakt)
Denken Sie nicht, dass Sie davon Abstand nehmen? **Auf keinen Fall! ** ** **
So etwas reicht nicht aus.
 Die Infektionsrate ist nach einem Jahr auf fast 50% gesunken, aber noch lange nicht konvergiert.
In dieser Welt können die Olympischen Spiele nicht stattfinden, selbst wenn sie um ein Jahr verschoben werden.
Die Infektionsrate ist nach einem Jahr auf fast 50% gesunken, aber noch lange nicht konvergiert.
In dieser Welt können die Olympischen Spiele nicht stattfinden, selbst wenn sie um ein Jahr verschoben werden.
Fall der Bevölkerungsdichte = 3% (70% weniger Kontakt)
Ist es notwendig, 70% statt 80% zu haben?
** Ja, 70% sind nicht gut. ** ** **
 Die Infektionsrate ist sicherlich recht niedrig, steigt jedoch seit fast einem Jahr, wenn auch langsam (gegen Ende leicht an).
Obwohl die Infektionsgeschwindigkeit unterdrückt wurde, scheint ein Jahr nicht genug zu sein, um eine natürliche Konvergenz zu erreichen.
Die Infektionsrate ist sicherlich recht niedrig, steigt jedoch seit fast einem Jahr, wenn auch langsam (gegen Ende leicht an).
Obwohl die Infektionsgeschwindigkeit unterdrückt wurde, scheint ein Jahr nicht genug zu sein, um eine natürliche Konvergenz zu erreichen.
Fall der Bevölkerungsdichte = 2% (80% weniger Kontakt)
** Die Anzahl der Neuinfektionen und die Anzahl der Heiler sind nahezu ausgeglichen. ** ** **
 Obwohl die neue Infektionsrate und die Heilungsrate angemessen festgelegt wurden, war das Ergebnis ziemlich schön.
Ich bin ein absoluter Amateur, aber ist die Anzahl der 80% weniger Kontakt eine Art Faustregel in der Infektionswissenschaft?
Obwohl die neue Infektionsrate und die Heilungsrate angemessen festgelegt wurden, war das Ergebnis ziemlich schön.
Ich bin ein absoluter Amateur, aber ist die Anzahl der 80% weniger Kontakt eine Art Faustregel in der Infektionswissenschaft?
Fall der Bevölkerungsdichte = 1% (90% weniger Kontakt)
** Die Anzahl der Infizierten wurde in etwas mehr als 200 Tagen 0. ** ** **
 Ich hoffe die reale Welt wird bald so sein ~
Ich hoffe die reale Welt wird bald so sein ~
Python-Code
Dies ist eine Spezifikation, die eine Animation zeichnet, die sich in Echtzeit ändert. Wenn der Zellenwert 0 ist, gibt es niemanden, -1 zeigt eine gesunde Person an und +1 zeigt eine infizierte Person an.
import numpy as np
from numpy import random
import seaborn as sns
import matplotlib.pyplot as plt
sns.set()
# parameter
density = 0.03
prob_infect = 0.20
prob_heal = 0.02
infected_initial = 0.05
# initialize earth
earth = np.where((random.random(10000) > (1 - density)), -1, 0).reshape(100, 100)
for i in range(int(10000 * density * infected_initial)):
earth[random.randint(0, 100), random.randint(0, 100)] = 1
time = 0
infection_ratio = np.zeros(10 ** 6) * np.nan
infection_ratio[time] = 0
plt.close()
fig, ax = plt.subplots(figsize=(12, 6), nrows=1, ncols=2)
no_end = True
while no_end:
for (x, y) in [(x, y) for x in range(100) for y in range(100)]:
if earth[x, y] != 0:
# infection
(x_min, x_max) = (max(x - 1, 0), min(x + 1, 98) + 1)
(y_min, y_max) = (max(y - 1, 0), min(y + 1, 98) + 1)
if np.any(earth[x_min: x_max, y_min: y_max] == 1):
earth[x, y] = 1 if random.rand() < prob_infect else earth[x, y]
# healing
earth[x, y] = -1 if random.rand() < prob_heal else earth[x, y]
# random walk around
x_next = min(max(x + random.randint(-1, 2), 0), 99)
y_next = min(max(y + random.randint(-1, 2), 0), 99)
if ((x_next, y_next) != (x, y)) & (earth[x_next, y_next] == 0):
earth[x_next, y_next] = earth[x, y]
earth[x, y] = 0
time += 1
infection_ratio[time] = np.sum(np.where(earth == 1, 1, 0)) / (10000 * density) * 100
try:
subplot0.cla()
subplot1.cla()
except:
print('no need to refresh figure')
plt.suptitle('time: {}'.format(time))
subplot0 = sns.heatmap(earth, vmin=-1, vmax=1, center=0, cmap='coolwarm', ax=ax[0], cbar=False)
ax[0].axis('off')
ax[0].set_title('density: {}%'.format(int(density * 100)))
subplot1 = sns.lineplot(data=infection_ratio)
ax[1].set_title('time series of infection')
ax[1].set_xlabel('time')
ax[1].set_ylabel('infection ratio %')
ax[1].set_ylim([0, 100])
ax[1].set_xlim([0, time + 10])
plt.tight_layout()
plt.draw()
plt.pause(0.01)
Recommended Posts