[PYTHON] Ich habe versucht, den besten Weg zu finden, um einen guten Ehepartner zu finden

Nach der derzeitigen Rate unverheirateter Personen auf Lebenszeit in Japan war jeder vierte Mann und jede siebte Frau erst im Alter von fünfzig Jahren verheiratet, und der Anteil dieser Menschen wird weiter zunehmen. (Quelle: Huffington Post). Es scheint verschiedene Ursachen zu geben, aber es scheint, dass der Grund ** "Ich kann nicht die richtige Person treffen" ** ganz oben steht.

Aber welche Art von Person ist die richtige Person?

Es gibt verschiedene Bedingungen, die Menschen voneinander wollen, wie Jahreseinkommen, Aussehen, Persönlichkeit, Zuhause usw. Sie verpassen oft eine Gelegenheit, während Sie sich fragen, ob Sie sich treffen können ... "(Tränen)

Das Problem ist, wenn Herr A nach einem Ehepartner sucht,

1. Herr A trifft N Personen und Frauen, die Kandidaten für eine Ehe sind
2. Kandidatengegner erscheinen nacheinander
3. Kandidatengegner haben unterschiedliche Punktzahlen
4. Herr A möchte eine Person mit der höchstmöglichen Punktzahl heiraten
5. Kandidaten können heiraten, wenn Herr A Ja sagt. Aber ich kann den Rest der Kandidaten nicht mehr treffen
6. Die Kandidaten werden gehen, wenn Herr A Nein sagt und sich nicht mehr treffen kann

Es kann zu einem Spiel mit der Regel vereinfacht werden. Dieses Problem wird als ** Sekretärsproblem ** bezeichnet und es gibt eine mathematisch optimale Strategie. das ist,

1. Die ersten 37% sagen Nein, unabhängig von der Punktzahl
2. Wenn Personen danach die höchste Punktzahl aller Zeiten erzielen, entscheiden Sie sich für diese Person

Es ist wirklich einfach. Genau genommen entsprechen 37% ** 1 / e **. Diese Strategie scheint die Chancen zu erhöhen, einen Gegner mit hoher Punktzahl zu heiraten, unabhängig von der Anzahl der Kandidatengegner N.

Selbst wenn ich das höre, denke ich ehrlich: "Ist es wirklich?" Ich verstehe, dass ich irgendwo einen Schwellenwert festlegen muss, aber ich habe das Gefühl, dass ich nach längerem Warten einen besseren Partner finden kann, z. B. 50% oder 80%, anstatt des ungeraden Werts von 37%.

Dieses Mal möchte ich eine einfache Simulation verwenden, um diese Strategie zu testen.

Strategieumsetzung

Ich werde mit Python3 rechnen. Geben Sie zunächst die erforderlichen Bibliotheken ein.

# import libraries
import random
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

Die Hauptfunktion verwendet als Eingabe die Anzahl der Kandidaten und die Anzahl der Personen, die sich vor dem Erstellen eines Schwellenwerts treffen, und wählt die Person aus, die den Schwellenwert zum ersten Mal überschreitet. Der Rang und die Punktzahl des Gegners werden ausgegeben. Angenommen, die Punktzahl des Kandidaten nimmt einen zufälligen ganzzahligen Wert von 0 bis 100 an.

# function to find a partner based on a given decision-time
def getmeplease(rest, dt, fig):
    ## INPUT: rest ... integer representing the number of the fixed future encounters
    #         dt ... integer representing the decision time to set the threshold
    #         fig ... 1 if you want to plot the data
    # ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    
    # score ranging from 0 to 100
    scoremax = 100
    #random.seed(1220)
    
    # sequence of scores 
    distribution = random.sample(range(scoremax), k=rest)
    
    # visualize distribution
    if fig==1:
        # visualize distribution of score
        plt.close('all')
        plt.bar(range(1,rest+1), distribution, width=1)
        plt.xlabel('sequence')
        plt.ylabel('score')
        plt.xlim((0.5,rest+0.5))
        plt.ylim((0,scoremax))
        plt.xticks(range(1, rest+1))

    # remember the highest score among the 100 x dt %
    if dt > 0:
        threshold = max(distribution[:dt])
    else:
        threshold = 0
    
    # pick up the first one whose score exceeds the threshold
    partner_id = 1
    partner_score = distribution[0]
    t = dt
    for t in range(dt+1, rest):
        if partner_score < threshold:
            partner_score = distribution[t]
        else:
            partner_id = t
            break
    else:
        partner_score = distribution[-1]
        partner_id = rest
        
    # get the actual ranking of the partner
    array = np.array(distribution)
    temp = array.argsort()
    ranks = np.empty(len(array), int)
    ranks[temp] = np.arange(len(array))
    partner_rank = rest - ranks[partner_id-1]
            
    # visualize all
    if fig==1:
        plt.plot([decisiontime+0.5,decisiontime+0.5],[0,scoremax],'--k')
        plt.bar(partner_id,partner_score, color='g', width=1)   
    
    return [partner_id, partner_score, partner_rank]

Wenn beispielsweise die Anzahl der Kandidaten 10 beträgt und die Anzahl der Personen, die Sie treffen, bevor Sie einen Schwellenwert festlegen, 4 Personen beträgt, was etwa 37% davon entspricht, zeichnet diese Funktion getmeplease (10,4,1) das folgende Diagramm.

Ich konnte die Person mit der höchsten Punktzahl heiraten, die auf Platz 8 von 10 Personen erschien ((((o ﾉ ´3 ｀) ﾉ awesome (weiße Augen))).

Simulation

Bereiten Sie 4 Muster von 5, 10, 20, 100 für die Anzahl der Personen vor, die N treffen sollen. Ebenso möchte ich vier Strategiemuster vorbereiten und vergleichen, wenn die Anzahl der Personen, die vor dem Erstellen eines Schwellenwerts angetroffen wurden, auf 10%, 37%, 50%, 80% der Gesamtzahl geändert wird.

In der folgenden Funktion wird jede Strategie ("optimal": 37%, "früh": 10%, "spät": 80%, "halb": 50%) 10000 Mal mit dem Rang des ausgewählten Gegners simuliert. Machen Sie ein Histogramm der Ergebnisse und finden Sie den Median.

# parameters
repeat = 10000
rest = [5,10,20,100]
opt_dt = [int(round(x/np.exp(1))) for x in rest]
tooearly_dt = [int(round(x*0.1)) for x in rest]
toolate_dt = [int(round(x*0.8)) for x in rest]
half_dt = [int(round(x*0.5)) for x in rest]

# initialization
opt_rank = np.zeros(repeat*len(rest))
early_rank = np.zeros(repeat*len(rest))
late_rank = np.zeros(repeat*len(rest))
half_rank = np.zeros(repeat*len(rest))
opt_score = np.zeros(repeat*len(rest))
early_score = np.zeros(repeat*len(rest))
late_score = np.zeros(repeat*len(rest))
half_score = np.zeros(repeat*len(rest))

# loop to find the actual rank and score of a partner
k = 0
for r in range(len(rest)):
    for i in range(repeat):    
        # optimal model
        partner_opt = getmeplease(rest[r], opt_dt[r], 0)
        opt_score[k] = partner_opt[1]
        opt_rank[k] = partner_opt[2]
        
        # too-early model
        partner_early = getmeplease(rest[r], tooearly_dt[r], 0)
        early_score[k] = partner_early[1]
        early_rank[k] = partner_early[2]
        
        # too-late model
        partner_late = getmeplease(rest[r], toolate_dt[r], 0)
        late_score[k] = partner_late[1]
        late_rank[k] = partner_late[2]
        
        # half-time model
        partner_half = getmeplease(rest[r], half_dt[r], 0)
        half_score[k] = partner_half[1]
        half_rank[k] = partner_half[2]
        
        k += 1
        
# visualize distributions of ranks of chosen partners
plt.close('all')
begin = 0
for i in range(len(rest)):
    plt.figure(i+1)
    
    plt.subplot(2,2,1)
    plt.hist(opt_rank[begin:begin+repeat],color='blue')
    med = np.median(opt_rank[begin:begin+repeat])
    plt.plot([med, med],[0, repeat*0.8],'-r')
    plt.title('optimal: %i' %int(med))
    
    plt.subplot(2,2,2)
    plt.hist(early_rank[begin:begin+repeat],color='blue')
    med = np.median(early_rank[begin:begin+repeat])
    plt.plot([med, med],[0, repeat*0.8],'-r')
    plt.title('early: %i' %int(med))
    
    plt.subplot(2,2,3)
    plt.hist(late_rank[begin:begin+repeat],color='blue')
    med = np.median(late_rank[begin:begin+repeat])
    plt.plot([med, med],[0, repeat*0.8],'-r')
    plt.title('late: %i' %int(med))
    
    plt.subplot(2,2,4)
    plt.hist(half_rank[begin:begin+repeat],color='blue')
    med = np.median(half_rank[begin:begin+repeat])
    plt.plot([med, med],[0, repeat*0.8],'-r')
    plt.title('half: %i' %int(med))
        
    fig = plt.gcf()
    fig.canvas.set_window_title('rest' + ' ' + str(rest[i]))
    
    begin += repeat
    
    plt.savefig(figpath + 'rank_' + str(rest[i]))

begin = 0
for i in range(len(rest)):
    plt.figure(i+10)
    
    plt.subplot(2,2,1)
    plt.hist(opt_score[begin:begin+repeat],color='green')
    med = np.median(opt_score[begin:begin+repeat])
    plt.plot([med, med],[0, repeat*0.8],'-r')
    plt.title('optimal: %i' %int(med))
    
    plt.subplot(2,2,2)
    plt.hist(early_score[begin:begin+repeat],color='green')
    med = np.median(early_score[begin:begin+repeat])
    plt.plot([med, med],[0, repeat*0.8],'-r')
    plt.title('early: %i' %int(med))
    
    plt.subplot(2,2,3)
    plt.hist(late_score[begin:begin+repeat],color='green')
    med = np.median(late_score[begin:begin+repeat])
    plt.plot([med, med],[0, repeat*0.8],'-r')
    plt.title('late: %i' %int(med))
    
    plt.subplot(2,2,4)
    plt.hist(half_score[begin:begin+repeat],color='green')
    med = np.median(half_score[begin:begin+repeat])
    plt.plot([med, med],[0, repeat*0.8],'-r')
    plt.title('half: %i' %int(med))
        
    fig = plt.gcf()
    fig.canvas.set_window_title('rest' + ' ' + str(rest[i]))

    begin += repeat
    
    plt.savefig(figpath + 'score_' + str(rest[i]))
    

Wenn N = 20

Wenn Sie 20 Personen treffen, ist die Verteilung der Punktzahlen und Ränge wie folgt.

Rang

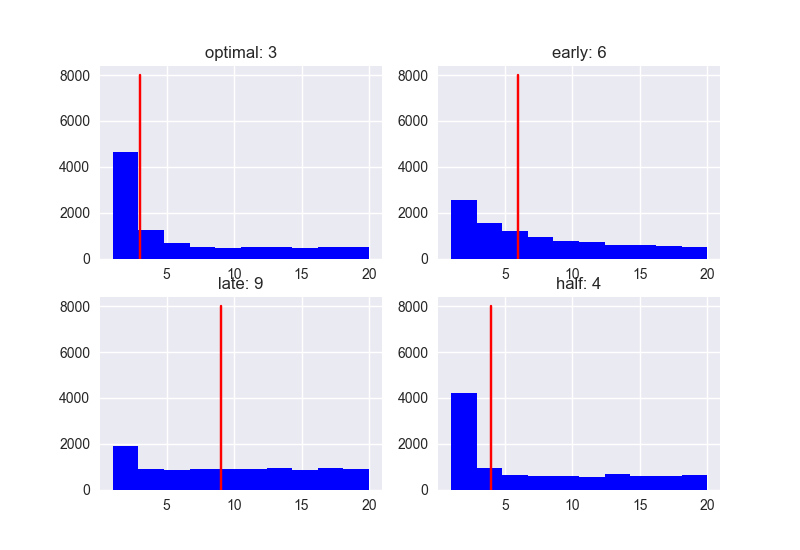
Mit der Optimal-Strategie (37%) betrug der Median-Rang 3. Wenn Sie sich mit der Strategie "Nein für die ersten 37%, dann Ja für die Person mit der höchsten Punktzahl" nähern, können Sie die Person innerhalb des Drittels der Personen heiraten, die Sie mit hoher Wahrscheinlichkeit treffen können. ..

Übrigens sind die Medianwerte für Early (10%) und Half (50%) 6 bzw. 4, es ist also überhaupt nicht schlecht (?). Spät (80%) hat einen Median von 9, also sind die Ausfallwahrscheinlichkeiten hoch. .. ..

Wie wäre es mit der Partitur?

Mit der Optimal-Strategie (37%) betrug der Medianwert 89. Andere Strategien haben 78 für Früh (10%), 59 für Spät (80%) und 86 für Halb (80%), sodass die Leistung immer noch hoch ist, wenn der Schwellenwert auf ** 1 / e ** festgelegt ist. nicht wahr. Es scheint einfacher zu sein, sich für eine bessere Person zu entscheiden. Die beste Strategie führt nicht immer zur besten Lösung, kann jedoch die Wahrscheinlichkeit erhöhen, sich der besten Lösung zu nähern.

Als Bonus werde ich auch die Anzahl der Kandidaten für 5, 10 und 100 auflisten.

N = 5 ### Rang

Ergebnis

N = 10 ### Rang

Ergebnis

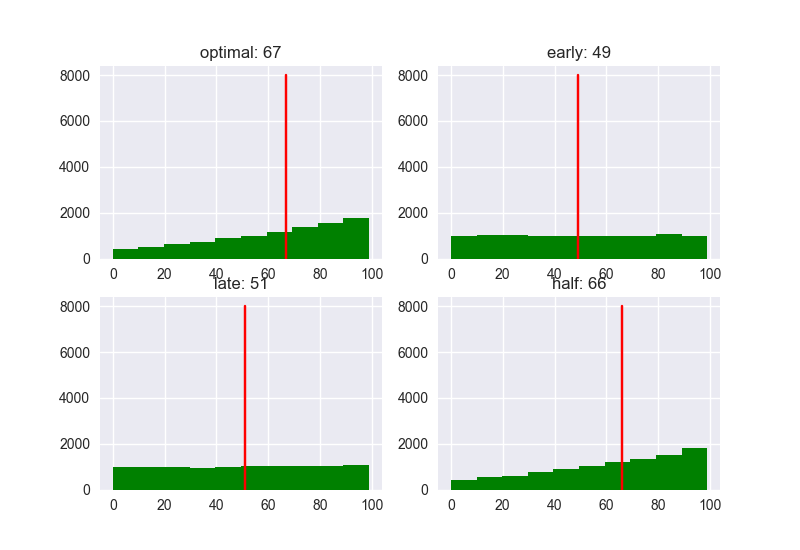
N = 100 ### Rang

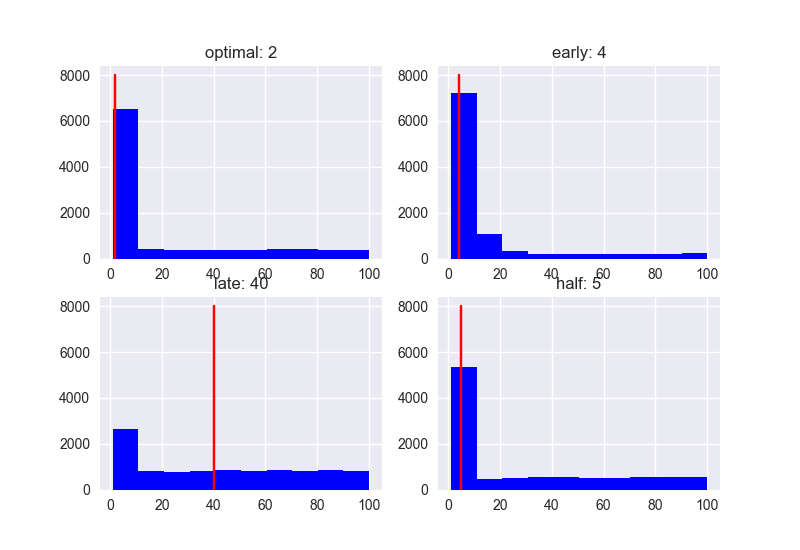
Ergebnis

Der offensichtliche Trend ist, dass die Leistung von "spät" mit zunehmender Anzahl von Kandidaten schlechter wird. Wenn die Anzahl der Kandidaten gering ist, ist der Leistungsunterschied in Abhängigkeit von der Strategie gering, aber der Bewertungswert ist tendenziell niedrig. In jedem Fall ist es wahrscheinlich, dass die Strategie, zuerst 37% der Menschen zu treffen, um den Schwellenwert festzulegen, die Strategie mit dem höchsten Rang und der höheren Punktzahl ist.

Fazit

―― Je mehr Kandidaten Sie haben, desto wahrscheinlicher ist es, dass Sie bessere Gegner treffen. ――Jedoch, wenn Sie mit "mehr denken ..." durcheinander kommen, verlieren Sie nicht nur Chancen, sondern auch die Punktzahl der letzten Person wird sich verschlechtern. »Aber es ist egal, ob es zu früh ist ――Es scheint die beste Strategie zu sein, die Anzahl der Personen zu bestimmen, die Sie in Zukunft treffen werden, die 1 / e-Personen zu treffen, um den Schwellenwert festzulegen, und dann die Person zu bestimmen, die den Schwellenwert zum ersten Mal überschreitet.

Hinweis

――In Wirklichkeit sagt die andere Partei oft Nein, selbst wenn Sie Ja sagen. ―― ~~ Leute, die an Feiertagen zu Hause Code schreiben ~~ haben oft überhaupt keine Kandidaten

• ** Die Annahme der optimalen Strategie bedeutet nicht, dass Sie die optimale Lösung erhalten **

……Geben wir unser Bestes!

Referenz

Huffington Post Article TED-Vorlesung * Hannah Fly-Mathematics, um über Liebe zu sprechen- [Der Artikel der Washington Post](https://www.washingtonpost.com/news/wonk/wp/2016/02/16/when-to-stop-dating-and-settle-down-according-to-math/ utm_term = .ee305554c210)