Ich habe eine Zusammenfassung von Cross Validation, Hyperparameter-Bestimmung, ROC-Kurve, AUC usw. und eine Ausführungsdemo in Python in Bezug auf die nüchterne, aber wichtige "Modellbewertung / Index" geschrieben.

Dieser Artikel ist der 7. Tag von Qiita Machine Learning Adventskalender 2015. Als ich es mir ansah, war 12/7 kostenlos, also schrieb ich es in Eile: grinsen:

Den vollständigen Code finden Sie im GitHub-Repository hier [https://github.com/matsuken92/Qiita_Contents/blob/master/Model_evaluation/Model_evaluation.ipynb].

0. Datensatz "Titanic"

Verwenden Sie den bekannten Titanic-Datensatz. Daten über Überlebende des Passagierschiffs Titanic, die häufig als Klassifizierungsdemonstrationsdaten verwendet werden.

Zunächst Vorverarbeitung und Datenimport

Ich habe einen Datensatz in Seaborn, also werde ich ihn verwenden.

%matplotlib inline
import numpy as np
import pandas as pd
from time import time
from operator import itemgetter

import matplotlib as mpl
import matplotlib.pyplot as plt
from tabulate import tabulate
import seaborn as sns
sns.set(style="whitegrid", color_codes=True)

from sklearn import cross_validation
from sklearn import datasets
from sklearn import svm
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import cross_val_score
from sklearn import grid_search

from sklearn.cross_validation import KFold
from sklearn.cross_validation import StratifiedKFold

from sklearn.metrics import classification_report, roc_auc_score, precision_recall_curve, auc, roc_curve

titanic = sns.load_dataset("titanic")

Dies sind die Daten. Die ersten 5 Zeilen werden angezeigt.

headers = [c for c in titanic.columns]
headers.insert(0,"ID")
print tabulate(titanic[0:5], headers, tablefmt="pipe")

ID	survived	pclass	sex	age	sibsp	fare	embarked	class	who	adult_male	deck	embark_town	alive	alone
0	0	3	male	22	1	7.25	S	Third	man	1	nan	Southampton	no	0
1	1	1	female	38	1	71.2833	C	First	woman	0	C	Cherbourg	yes	0
2	1	3	female	26	0	7.925	S	Third	woman	0	nan	Southampton	yes	1
3	1	1	female	35	1	53.1	S	First	woman	0	C	Southampton	yes	0
4	0	3	male	35	0	8.05	S	Third	man	1	nan	Southampton	no	1

#Machen Sie kategoriale Variablen zu Dummy-Variablen
def convert_dummies(df, key):
    dum = pd.get_dummies(df[key])
    ks = dum.keys()
    print "Removing {} from {}...".format(ks[0], key)
    dum.columns = [key + "_" + str(k) for k in ks]  
    df = pd.concat((df, dum.ix[:,1:]), axis=1)
    df = df.drop(key, axis=1)
    return df

titanic = convert_dummies(titanic, "who")
titanic = convert_dummies(titanic, "class")
titanic = convert_dummies(titanic, "sex")
titanic = convert_dummies(titanic, "alone")
titanic = convert_dummies(titanic, "embark_town")
titanic = convert_dummies(titanic, "deck")
titanic = convert_dummies(titanic, "embarked")

titanic['age'] = titanic.age.fillna(titanic.age.median())
titanic['adult_male'] = titanic.adult_male.map( {True: 1, False: 0} ).astype(int)
titanic['alone'] = titanic.adult_male.map( {True: 1, False: 0} ).astype(int)

#Nicht verwendete Variablen löschen
titanic = titanic.drop("alive", axis=1)
titanic = titanic.drop("pclass", axis=1)

1. Aufteilen des Datensatzes

1-1. Holdout-Methode

Ein bestimmter Prozentsatz der Daten mit Lehrern, die wir jetzt haben, ist in "Trainingsdaten" und "Testdaten" zum Lernen und Auswerten unterteilt. Wenn beispielsweise das Verhältnis von Trainingsdaten zu Testdaten 80:20 beträgt, sieht es so aus.

#Trainingsdaten(80%),Testdaten(20%)Teilen in
target = titanic.ix[:, 0]
data = titanic.ix[:, [1,2,3,4,5,6,7,8,9,10,11,12,14]]
X_train, X_test, y_train, y_test = cross_validation.train_test_split(data, target, test_size=0.2, random_state=None)

print [d.shape for d in [X_train, X_test, y_train, y_test]]

`out`


[(712, 23), (179, 23), (712,), (179,)]

Das Erhöhen der Menge an Trainingsdaten erhöht die Genauigkeit des Lernens, verringert jedoch die Genauigkeit der Modellbewertung.
Das Erhöhen der Menge an Testdaten erhöht die Genauigkeit der Modellbewertung, verringert jedoch die Genauigkeit des Lernens.

Achten Sie auf den Kompromiss und bestimmen Sie das Verhältnis.

# SVM(Linearer Kernel)Klassifizieren nach und berechnen Sie die Fehlerrate
clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
print u"Fehlerrate bei Neuzuweisung:", 1 - clf.score(X_train, y_train)   
print u"Holdout-Fehlerrate:", 1 - clf.score(X_test, y_test)

`out`


Neuzuweisungsfehlerrate: 0.162921348315
Holdout-Fehlerrate: 0.212290502793

# SVM(RBF-Kernel)Klassifizieren nach und berechnen Sie die Fehlerrate
clf = svm.SVC(kernel='rbf', C=1).fit(X_train, y_train)
print u"Fehlerrate bei Neuzuweisung:", 1 - clf.score(X_train, y_train)   
print u"Holdout-Fehlerrate:", 1 - clf.score(X_test, y_test)

`out`


Neuzuweisungsfehlerrate: 0.101123595506
Holdout-Fehlerrate: 0.268156424581

1-2. Kreuzvalidierung (CV): k-fach geschichtet

K-fold Zunächst zur einfachen K-Falte. Betrachten Sie den Fall, in dem 30 Daten vorhanden sind. n_folds ist die Anzahl der Unterteilungen, dividiert den jetzt vorhandenen Datensatz durch die Anzahl der Unterteilungen und gibt alle Kombinationen in Form einer tiefgestellten Liste aus, wie unten gezeigt. Dies sind die Testdaten.

 # KFold
# n_Teilen Sie die Daten durch den durch Falten angegebenen numerischen Wert. n_folds=Wenn es 5 ist, wird es in 5 geteilt
#Dann wird eines davon als Testdaten verwendet und fünf Muster werden erzeugt.
kf = KFold(30, n_folds=5,shuffle=False)
for tr, ts in kf:
    print("%s %s" % (tr, ts))

`out`


[ 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29] [0 1 2 3 4 5]
[ 0  1  2  3  4  5 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29] [ 6  7  8  9 10 11]
[ 0  1  2  3  4  5  6  7  8  9 10 11 18 19 20 21 22 23 24 25 26 27 28 29] [12 13 14 15 16 17]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 24 25 26 27 28 29] [18 19 20 21 22 23]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] [24 25 26 27 28 29]

Stratified k-fold Aus dem obigen K-fachen ein Verfahren zum Teilen des Datensatzes, um jedes Klassenverhältnis in dem vorliegenden Datensatz beizubehalten. Der im nächsten Abschnitt verwendete cross_validation.cross_val_score übernimmt dies.

# StratifiedKFold
#Eine verbesserte Version von KFold, die die Extraktionsrate für jede Klasse an das Verhältnis der Originaldaten anpasst

label = np.r_[np.repeat(0,20), np.repeat(1,10)]
skf = StratifiedKFold(label, n_folds=5, shuffle=False)
for tr, ts in skf:
    print("%s %s" % (tr, ts))

`out`


[ 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 22 23 24 25 26 27 28 29] [ 0  1  2  3 20 21]
[ 0  1  2  3  8  9 10 11 12 13 14 15 16 17 18 19 20 21 24 25 26 27 28 29] [ 4  5  6  7 22 23]
[ 0  1  2  3  4  5  6  7 12 13 14 15 16 17 18 19 20 21 22 23 26 27 28 29] [ 8  9 10 11 24 25]
[ 0  1  2  3  4  5  6  7  8  9 10 11 16 17 18 19 20 21 22 23 24 25 28 29] [12 13 14 15 26 27]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 20 21 22 23 24 25 26 27] [16 17 18 19 28 29]

Versuche zu rennen

# SVM(Linearer Kernel)Klassifizieren nach und berechnen Sie die Fehlerrate
#Berechnen Sie jede Punktzahl mit der in 5 geteilten geschichteten K-Falte

clf = svm.SVC(kernel='rbf', C=1)
scores = cross_validation.cross_val_score(clf, data, target, cv=5,)
print "scores: ", scores
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))

Da 5 für "n_folds" angegeben ist, werden 5 verschiedene Bewertungen ausgegeben. Die Genauigkeit ist der Durchschnittswert und die Standardabweichung.

`out`


scores:  [ 0.67039106  0.70949721  0.74157303  0.74719101  0.78531073]
Accuracy: 0.73 (+/- 0.08)

2. Wie man bessere Hyperparameter findet

2-1. Exhaustive Grid Search Mit anderen Worten, es ist eine Möglichkeit, alle von Ihnen festgelegten Hyperparameter von Grund auf auszuprobieren, um herauszufinden, welcher der besten ist. Es wird einige Zeit dauern, aber wir werden alles versuchen, was Sie angeben, sodass Sie wahrscheinlich eine gute finden werden.

Stellen Sie zunächst die möglichen Werte der Parameter wie folgt ein.

param_grid = [
  {'kernel': ['rbf','linear'], 'C': np.linspace(0.1,2.0,20),}
 ]

Übergeben Sie es zusammen mit SVC (Support Vector Classifier) an grid_search.GridSearchCV und führen Sie es aus.

#Lauf
svc = svm.SVC(random_state=None)
clf = grid_search.GridSearchCV(svc, param_grid)
res = clf.fit(X_train, y_train)

#Ergebnisse anzeigen
print "score: ", clf.score(X_test, y_test)
print "best_params:", res.best_params_
print "best_estimator:", res.best_estimator_

Es probiert alle angegebenen Parameter aus und zeigt die Punktzahl mit dem besten Ergebnis, welcher Parameter gut war, und dem detaillierten angegebenen Parameter an.

`out`


 0.787709497207
 {'kernel': 'linear', 'C': 0.40000000000000002}
 SVC(C=0.40000000000000002, cache_size=200, class_weight=None, coef0=0.0,
  degree=3, gamma=0.0, kernel='linear', max_iter=-1, probability=False,
  random_state=None, shrinking=True, tol=0.001, verbose=False)

Dies dauerte jedoch immerhin einige Zeit. Wenn die Anzahl der Parameter, die Sie ausprobieren möchten, zunimmt, können Sie nicht alle sehen. Als nächstes werde ich eine Methode aufgreifen, die Zufälligkeit bei der Auswahl von Parametern berücksichtigt.

2-2. Randomized Parameter Optimization

Versuchen Sie, die Parameter zu erhöhen, die Sie ausprobieren möchten. Dieses Mal verwenden wir eine zufällige Gesamtstruktur mit vielen Parametern.

param_dist = {'n_estimators': range(4,20,2), 'min_samples_split': range(1,30,2), 'criterion':['gini','entropy']}

Lassen Sie es uns ausführen und sehen, wie lang die Verarbeitungszeit ist. (* Wenn die Anzahl der Parameterkombinationen 20 oder weniger beträgt, wird ein Fehler mit der Meldung "Grid Search verwenden" angezeigt.)

n_iter_search = 20
rfc = RandomForestClassifier(max_depth=None, min_samples_split=1, random_state=None)
random_search = grid_search.RandomizedSearchCV(rfc, 
                                   param_distributions=param_dist,
                                   n_iter=n_iter_search)
start = time()
random_search.fit(X_train, y_train)
end   = time()
print"Anzahl der Parameter: {0},verstrichene Zeit: {1:0.3f}Sekunden".format(n_iter_search, end - start)

`out`


Anzahl der Parameter: 20,verstrichene Zeit: 0.805 Sekunden

Die drei wichtigsten Parametereinstellungen sind unten aufgeführt.

#Top 3 Parameter
top_scores = sorted(random_search.grid_scores_, key=itemgetter(1), reverse=True)[:3]
for i, score in enumerate(top_scores):
    print("Model with rank: {0}".format(i + 1))
    print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
          score.mean_validation_score,
          np.std(score.cv_validation_scores)))
    print("Parameters: {0}".format(score.parameters))
    print("")

`out`


Model with rank: 1
Mean validation score: 0.834 (std: 0.007)
Parameters: {'min_samples_split': 7, 'n_estimators': 10, 'criterion': 'gini'}

Model with rank: 2
Mean validation score: 0.826 (std: 0.010)
Parameters: {'min_samples_split': 25, 'n_estimators': 18, 'criterion': 'entropy'}

Model with rank: 3
Mean validation score: 0.823 (std: 0.022)
Parameters: {'min_samples_split': 19, 'n_estimators': 12, 'criterion': 'gini'}

3. Bewertungsindex

Betrachten Sie als Beispiel das Diagnoseergebnis einer bestimmten Krankheit. Zu diesem Zeitpunkt gibt es vier mögliche Ergebnisse, wie unten gezeigt, basierend auf dem Diagnoseergebnis und dem wahren Wert. Die Tabelle ist wie folgt.

Basic,

T(true), F(false)
P(positive), N(negative)

Bei Prüfung mit der Kombination von true bedeutet "das Diagnoseergebnis und der wahre Wert stimmen überein", false bedeutet "das Diagnoseergebnis und der wahre Wert sind unterschiedlich" Positiv ist "krank", negativ ist "nicht krank" Repräsentiert.

Darauf aufbauend werden folgende Bewertungsindizes berechnet.

Richtige Antwortrate [Genauigkeit]

{\rm Accuracy = { TP + TN \over TP + FP + FN + TN}}

Präzisionsrate [Präzision]

Der Prozentsatz der richtigen Antworten unter denen, deren Diagnose positiv ist.

{\rm Precision = {TP \over TP + FP}}

Rückrufrate [Rückruf]

Richtige Antwortrate unter denen, deren wahrer Wert schlecht ist

{\rm Recall = {TP \over TP + FN}}

F-Wert (F-Maß)

Harmonisierter Durchschnitt von Präzision und Rückruf.

{\rm F-measure = {2\cdot Precision \cdot Recall \over Precision +Recall }}

3-1. Versuchen Sie zu berechnen

# SVM(Linearer Kernel)Klassifizieren nach und berechnen Sie den Bewertungsindex
clf = svm.SVC(kernel='linear', C=1, probability=True).fit(X_train, y_train)
print u"Accuracy:", clf.score(X_test, y_test)   
y_pred = clf.predict(X_test)
print classification_report(y_test, y_pred, target_names=["not Survived", "Survived"])

`out`


              precision    recall  f1-score   support

not Survived       0.80      0.86      0.83       107
    Survived       0.77      0.68      0.72        72

 avg / total       0.79      0.79      0.79       179

3-2. ROC und AUC

Ich werde den Index namens AUC erklären. Dies kann aus der ROC-Kurve (Receiver Operating Characteristic) abgeleitet werden, aber im vorherigen Artikel

[Statistik] Verstehen Sie anhand von Animationen, wie die ROC-Kurve aussieht.

Detaillierte Erläuterungen finden Sie hier in.

Die Fläche unter dieser ROC-Kurve ist AUC (Area Under the Curve). (Richtig ...: heat_smile :)

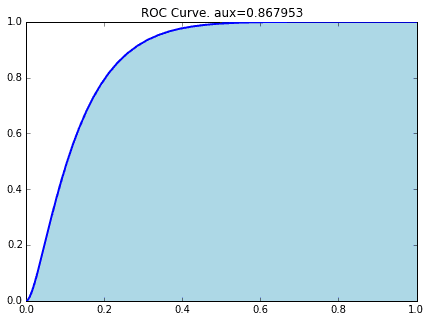
prob = clf.predict_proba(X_test)[:,1]
fpr, tpr, thresholds= roc_curve(y_test, prob)

plt.figure(figsize=(8,6))
plt.plot(fpr, tpr)
plt.title("ROC curve")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.show()

Die ROC-Kurve, wenn die Titanic-Daten durch SVM (Linear Kernel) klassifiziert werden, ist wie folgt.

#Berechnung der AUC
precision, recall, thresholds = precision_recall_curve(y_test, prob)
area = auc(recall, precision)
print "Area Under Curve: {0:.3f}".format(area)

`out`


Area Under Curve: 0.800

Referenz

WEB 　Scikit Learn User Guide 3. Model selection and evaluation 　　　http://scikit-learn.org/stable/model_selection.html

** Bücher ** "Erste Mustererkennung" Yuzo Hirai "Einführung in maschinelles Lernen für die Sprachverarbeitung" Manabu Okumura

[PYTHON] [Maschinelles Lernen] Zusammenfassung und Ausführung der Modellbewertung / Indikatoren (mit Titanic-Datensatz)

0. Datensatz "Titanic"

Zunächst Vorverarbeitung und Datenimport

1. Aufteilen des Datensatzes

1-1. Holdout-Methode

out

out

out

1-2. Kreuzvalidierung (CV): k-fach geschichtet

out

out

Versuche zu rennen

out

2. Wie man bessere Hyperparameter findet

out

out

out

3. Bewertungsindex

Richtige Antwortrate [Genauigkeit]

Präzisionsrate [Präzision]

Rückrufrate [Rückruf]

F-Wert (F-Maß)

3-1. Versuchen Sie zu berechnen

out

3-2. ROC und AUC

out

Referenz

`out`

`out`

`out`

`out`

`out`

`out`

`out`

`out`

`out`

`out`

`out`