[Harlem] Il y en a trop pour choisir! 13 façons de calculer la circonférence π en Python

Bonjour des abysses de l'univers!

\displaystyle\int {\rm d}\boldsymbol{r}\hat{\psi}^{\dagger}(\boldsymbol{r})Amis de Poppin\hat{\psi}(\boldsymbol{r})

est! Cette fois, je voudrais vous présenter ** 13 façons ** de calculer le rapport de circonférence $ \ pi $ avec Python **!

Auparavant, j'avais lu un article (célèbre dans le domaine du rapport de circonférence) intitulé "Ne vous inquiétez plus du rapport de circonférence! 10 façons de trouver π". , Le désir de «chercher π» a augmenté, j'ai donc décidé d'écrire cet article. Et cette fois, j'ai implémenté presque toutes les méthodes pour trouver $ \ pi $ dans l'article ** en Python!

Quand je l'ai essayé, ** connaissances de base de Python ** (fonctions, Numpy, pour les instructions, tandis que les instructions, les instructions if, les classes, etc.) étaient incluses ** abondamment **, donc la programmation (comme moi) Je le recommande vivement aux débutants pour pratiquer Python!

L'environnement est le suivant.

--PC: MacBook Pro (15 pouces, 2018)

• Processeur: Intel Core i7 6 cœurs à 2,2 GHz --Mémoire: 16 Go de DDR4 à 2400 MHz
• Environnement Python: Anaconda, Jupyter Notebook (6.0.1), python 3.7.4

Alors, profitez du Harlem ** tissé selon les méthodes de calcul du rapport de circonférence!

Utilisez les fonctions de base de Numpy

Python a une bibliothèque appelée Numpy (fournie par Anaconda depuis le début) et possède des fonctionnalités très utiles pour les calculs vectoriels, matriciels et autres calculs mathématiques. Ci-dessous, nous allons vous montrer comment calculer le rapport de circonférence avec les fonctions de base de Numpy!

1. numpy.pi La première consiste à utiliser ** numpy.pi **. Dans Numpy, il y a un gars qui donne la valeur du rapport de circonférence appelé numpy.pi, et c'est le plus rapide à utiliser. Je ne le calcule même plus w

import numpy as np #Importer numpy

pi = np.pi #Np à la variable pi.Remplacer pi
print(pi) #production

La sortie ressemble à ceci:

3.141592653589793

2. Fonction inverse du bronzage

Supposons que vous soyez soudainement frappé par ** "une malédiction que seul numpy.pi ne peut pas être utilisé parmi les fonctionnalités de Numpy" **.

Maintenant c'est dur! Vous ne pouvez pas obtenir le rapport de circonférence par la première méthode! Cependant, d'autres fonctionnalités de Numpy sont toujours disponibles, alors explorons d'autres moyens. À propos, il existe une méthode légendaire qui a été transmise depuis la préhistoire. C'est une façon d'utiliser ** la fonction inverse de tan **.

\tan\left(\frac{\pi}{4}\right)=1\Longleftrightarrow\arctan(1)=\frac{\pi}{4}\tag{1}

Si vous profitez d'être

\pi = 4\arctan(1) \tag{2}

Peut être demandé. Faisons le!

import numpy as np

pi = 4 * np.arctan(1) #Variable pi à 4*tanh(1)Remplacer
print(pi) #production

La sortie ressemble à ceci:

3.141592653589793

J'ai eu exactement le même résultat que la première méthode! D'ailleurs, cette méthode a été transmise depuis l'ère préhistorique lorsque ** Fortran **, la première «langue» de l'humanité, est né. C'est la sagesse de nos prédécesseurs!

Obtenu dans la région

** "L'aire d'un cercle avec un rayon de $ r $ est $ S = \ pi r ^ 2 $" ** Comme vous le savez tous, c'est un sens commun universel profondément gravé dans la psychologie profonde de toute l'humanité! Dans ce qui suit, trouvons le rapport de circonférence en utilisant l'aire de ce cercle que tout le monde connaît!

3. Approximation régulière des polygones

En augmentant l'aire du carré positif $ n $ inscrit dans le cercle, la valeur se rapproche de plus en plus de l'aire du cercle. L'aire d'un carré $ n $ positif inscrit dans un cercle de rayon $ r $ est

S_n=n\times\frac{r^2}{2}\sin\left(\frac{360^\circ}{n}\right)\to\pi r^2\ (n\to\infty) \tag{3}

Est requis à. Implémentons-le en supposant que le rayon est $ r = 1 $!

import numpy as np

#Approximation polygonale
def RegularPolygon(N):
    theta = np.radians(360 / N) #Divisez 360 ° en N parties égales et passez de la méthode de fréquence à la méthode de degré d'arc
    pi = N * np.sin(theta) / 2 #Calculez l'aire d'un N-côtés régulier
    return pi

#production
print("RegularPolygon(100)     = " + str(RegularPolygon(100)))
print("RegularPolygon(1000)    = " + str(RegularPolygon(1000)))
print("RegularPolygon(10000)   = " + str(RegularPolygon(10000)))
print("RegularPolygon(100000)  = " + str(RegularPolygon(100000)))
print("RegularPolygon(1000000) = " + str(RegularPolygon(1000000)))

La fonction «np.radius ()» utilisée dans le code est une fonction qui dépend de la valeur du rapport de circonférence, et il est personnel d'utiliser la fonction qui dépend du rapport de circonférence pour trouver le rapport de circonférence. C'est désagréable, mais je ne pouvais penser à aucun autre bon moyen, alors je le laisse tel quel cette fois (s'il vous plaît laissez-moi savoir si vous connaissez un bon moyen).

Le résultat de sortie est le suivant. Il s'approche progressivement du ratio de circonférence!

RegularPolygon(100)     = 3.1395259764656687
RegularPolygon(1000)    = 3.141571982779475
RegularPolygon(10000)   = 3.141592446881286
RegularPolygon(100000)  = 3.141592651522708
RegularPolygon(1000000) = 3.1415926535691225

4. Intégration numérique (approximation rectangulaire)

Il existe d'autres façons de trouver l'aire d'un cercle en plus de l'approximation polygonale. Cette fois, utilisons l'idée de ** intégration ** (produit partitionné).

Pensez à trouver la fonction $ y = f (x) $, la ligne droite $ x = a, \ x = b \ (a <b) $, et la zone $ S $ de la partie entourée par l'axe $ x $. $ x $ L'intervalle d'axe $ [a, \ b] $ est divisé en $ n $ parties égales, et les parties égales sont $ x_0, \ x_1, \ x_2, \ cdots, \ x_n \ (où \ x_0 = a, \ x_n = b) $. Aussi, laissez l'intervalle entre les points de division adjacents être $ \ Delta x = (b-a) / n $. A ce moment, l'aire $ S_i $ de la partie de l'intervalle $ [x_i, \ x_ {i + 1}] $ est ** $ S_i = f (x_i) \ Delta x $ **, c'est-à-dire que la base est $ \ Delta x. Approximative ** sous forme de rectangle avec $ et hauteur $ f (x_i) $. Après cela, trouvez $ S_i $ pour tous les intervalles $ [x_i, \ x_ {i + 1}] \ (i = 0, \ 2, \ cdots, \ n-1) $, et additionnez-les pour obtenir une approximation. La zone $ S_n $ peut être obtenue. Ensuite, si vous augmentez le nombre $ n $ qui divise l'intervalle $ [a, \ b] $ en parties égales, il finira par s'approcher de la vraie zone $ S $.

S_n = \sum_{i=0}^{n-1} f(x_i)\frac{b-a}{n}\to S\ (n\to\infty) \tag{4}

Appliquons cette méthode à l'aire d'un cercle. L'équation du cercle unitaire (centre d'origine, rayon 1) dans le plan $ x-y $ est

x^2+y^2=1\Longleftrightarrow y=\pm\sqrt{1-x^2} \tag{5}

Cependant, le plus un représente la moitié supérieure et le moins représente la moitié inférieure. Cette fois, trouvez l'aire de la partie (quart de cercle) de $ x> = 0 $ dans la moitié supérieure. L'intervalle de la surface à calculer est $ [a, \ b] = [0, \ 1] $, donc si cela est appliqué à la formule (4) du produit divisionnaire

S_n=\sum_{i=0}^{n-1} \frac{\sqrt{1-\left(\frac{i}{n}\right)^2}}{n}\to \frac{\pi}{4}\ (n\to\infty) \tag{6}

Ce sera.

Mettons-le en œuvre!

import numpy as np

#Une fonction d'approximation rectangle. section[0,1]Est divisé en N parties égales.
def Rectangle(N):
    x = np.arange(N) / N #0~(N-1)/Tableau de N éléments jusqu'à N
    y = np.sqrt(1 - x**2) #y=root(1-x^2)Calculer
    pi = 4 * np.sum(y) / N #Calculer la superficie
    return pi

#production
print("Rectangle(100)     = " + str(Rectangle(100)))
print("Rectangle(1000)    = " + str(Rectangle(1000)))
print("Rectangle(10000)   = " + str(Rectangle(10000)))
print("Rectangle(100000)  = " + str(Rectangle(100000)))
print("Rectangle(1000000) = " + str(Rectangle(1000000)))

Le résultat est le suivant

Rectangle(100)     = 3.160417031779046
Rectangle(1000)    = 3.1435554669110277
Rectangle(10000)   = 3.141791477611322
Rectangle(100000)  = 3.1416126164019866
Rectangle(1000000) = 3.141594652413813

La convergence est plus lente que l'approximation polygonale, mais la valeur converge vers la circonférence lorsque la division égale $ n $ augmente.

5. Intégration numérique (approximation trapézoïdale)

La précision est considérablement plus élevée que celle de l'approximation rectangulaire ** simplement en ajoutant ** une torsion au produit divisionnaire précédent. Auparavant, l'aire de la section des minutes était approximée par un rectangle, mais elle est ** base supérieure $ f (x_i) $, base inférieure $ f (x_ {i + 1}) $, hauteur $ \ Delta x $ À peu près comme un trapèze **. En d'autres termes, utilisez la formule suivante.

S_n = \sum_{i=0}^{n-1} \frac{f(x_i)+f(x_{i+1})}{2}\cdot\frac{b-a}{n}\to S\ (n\to\infty) \tag{7}

Comme vous pouvez le voir sur la figure ci-dessous, l'approximation rectangulaire a beaucoup de pièces supplémentaires ou manquantes en haut, mais la forme trapézoïdale le réduit considérablement.

Mettons-le en œuvre!

import numpy as np

#Approximation trapézoïdale
def Trapezoid(N):
    x = np.arange(N + 1) / N #0~Tableau d'éléments N + 1 jusqu'à 1
    y = np.sqrt(1 - x**2) #y=root(1-x^2)Calculer
    z = (y[0:N] + y[1:N+1]) / 2 #Trapézoïdale(Bas supérieur + bas inférieur)/Calculer 2
    pi = 4 * np.sum(z) / N #Calculer la superficie
    return pi

#production
print("Trapezoid(100)     = " + str(Trapezoid(100)))
print("Trapezoid(1000)    = " + str(Trapezoid(1000)))
print("Trapezoid(10000)   = " + str(Trapezoid(10000)))
print("Trapezoid(100000)  = " + str(Trapezoid(100000)))
print("Trapezoid(1000000) = " + str(Trapezoid(1000000)))

Voici le résultat de l'exécution. Elle est légèrement inférieure à l'approximation polygonale, mais on peut voir qu'elle converge plus vite que l'approximation rectangulaire.

Trapezoid(100)     = 3.1404170317790454
Trapezoid(1000)    = 3.141555466911028
Trapezoid(10000)   = 3.141591477611322
Trapezoid(100000)  = 3.1415926164019865
Trapezoid(1000000) = 3.1415926524138094

Obtenu de la série

Il existe un moyen d'exprimer le rapport de circonférence en utilisant une série infinie, qui est la somme d'un nombre infini de séquences. Utilisons-le pour trouver le rapport de circonférence! (De plus, la preuve est assez gênante voire impossible pour l'auteur, je vais donc l'omettre ...)

6. Classe de Bâle

On sait que le rapport de circonférence apparaît dans les classes suivantes.

1+\frac{1}{2^2}+\frac{1}{3^2}+\dots+\frac{1}{n^2}+\dots=\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6} \tag{8}

C'est une formule qui ajoute tous les nombres inverses des carrés des nombres naturels, mais étonnamment, le résultat inclut le rapport de circonférence. Quand je fais des mathématiques, il est intéressant de profiter du plaisir de "Est-ce que $ \ pi $ vient là-bas!" Cliquez ici pour plus de détails sur les séries de Bâle

Comme dans le cas de l'intégration numérique, il est impossible pour un ordinateur d'effectuer des opérations qui se poursuivent indéfiniment, donc ici la somme est coupée au milieu pour obtenir une valeur approximative. Mettons-le en œuvre!

import numpy as np

#Classe de Bâle. Calculez la somme jusqu'au Nième terme.
def Basel(N):
    x = np.arange(1, N + 1) #1~Tableau d'entiers naturels jusqu'à N
    pi = np.sqrt(6 * np.sum(1 / x**2)) #Calculez la somme inverse des carrés de chaque élément du tableau et multipliez par 6 en carré.
    return pi

#production
print("Basel(100)     = " + str(Basel(100)))
print("Basel(1000)    = " + str(Basel(1000)))
print("Basel(10000)   = " + str(Basel(10000)))
print("Basel(100000)  = " + str(Basel(100000)))
print("Basel(1000000) = " + str(Basel(1000000)))

Voici les résultats. Vous pouvez voir que lorsque le nombre de termes à additionner augmente, il converge vers le rapport de circonférence.

Basel(100)     = 3.132076531809106
Basel(1000)    = 3.1406380562059932
Basel(10000)   = 3.14149716394721
Basel(100000)  = 3.1415831043264415
Basel(1000000) = 3.1415916986604673

7. Classe Leibniz

Il existe d'autres classes dans lesquelles le rapport de circonférence sort. La classe Leibniz suivante en fait partie.

1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\dots+\frac{(-1)^{n-1}}{2n-1}+\dots=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{2n-1}=\frac{\pi}{4} \tag{9}

Cette fois, le calcul consiste à additionner les nombres inverses des nombres impairs alternativement plus et moins, mais le rapport de circonférence apparaît également ici! Cliquez ici pour plus de détails sur la série Leibniz

Implémentons-le de la même manière que la série de Bâle.

import numpy as np

#Classe Leibniz. Calculez la somme jusqu'au Nième terme.
def Leibniz(N):
    x = np.arange(1, N + 1) #1~Tableau d'entiers naturels jusqu'à N
    y = 1 / (2 * x - 1) #Calculer un tableau d'inverses impairs
    pm = (-1) ** (x - 1) #Calcul d'une séquence de nombres dans laquelle Pramai 1 est disposé en alternance
    pi = 4 * np.dot(y, pm) #Calculez la somme de l'alternance de Pramai par le produit interne de y et pm, et multipliez par 4 à la fin.
    return pi

#production
print("Leibniz(100)     = " + str(Leibniz(100)))
print("Leibniz(1000)    = " + str(Leibniz(1000)))
print("Leibniz(10000)   = " + str(Leibniz(10000)))
print("Leibniz(100000)  = " + str(Leibniz(100000)))
print("Leibniz(1000000) = " + str(Leibniz(1000000)))

Voici le résultat de l'exécution. Il converge en douceur!

Leibniz(100)     = 3.131592903558553
Leibniz(1000)    = 3.140592653839795
Leibniz(10000)   = 3.141492653590045
Leibniz(100000)  = 3.141582653589825
Leibniz(1000000) = 3.141591653589752

8. Classe Ramanujan

Enfin, je voudrais vous présenter la classe de type monstre ** "Ramanujan class" **. Voici la formule.

\begin{align}
\frac{1}{\pi} = \frac{2\sqrt{2}}{99^2}\sum_{n=0}^\infty\frac{(4n)!(1103+26390n)}{(396^{n}n!)^4} \tag{10}
\\
\frac{4}{\pi} = \sum_{n=0}^\infty\frac{(-1)^n(4n)!(1123+21460n)}{882^{2n+1}(4^n n!)^4} \tag{11}
\end{align}

Je ne comprends plus le sens. .. .. Ramanujan est un mathématicien indien qui a laissé derrière lui un certain nombre de formules incompréhensibles telles que celles ci-dessus. Aussi, lorsqu'on lui a demandé "Comment avez-vous organisé la cérémonie", il a répondu: "La déesse vous apprendra dans vos rêves." C'est un pervers. Cliquez ici pour plus de détails sur la classe Ramanujan [Cliquez ici pour Ramanujan](https://ja.wikipedia.org/wiki/%E3%82%B7%E3%83%A5%E3%83%AA%E3%83%8B%E3%83%B4% E3% 82% A1% E3% 83% BC% E3% 82% B5% E3% 83% BB% E3% 83% A9% E3% 83% 9E% E3% 83% 8C% E3% 82% B8% E3% 83% A3% E3% 83% B3)

Mettons-le en œuvre! Cette fois, je vais implémenter l'équation (11) dans mon humeur.

import numpy as np

#Numéro de classe Ramanujan. Résumez jusqu'au Nième terme.
def Ramanujan(N):
    sum = 0.0 #La valeur de la somme. Valeur initiale 0
    for i in range(N): #i est 0 à N-Faites moins de 1
        numerator = ((-1)**i) * np.math.factorial(4 * i) * (1123 + 21460 * i) #Calcul de la molécule de l'élément i
        denominator = (882**(2 * i + 1)) * ((4**i) * np.math.factorial(i))**4 #Calcul du dénominateur du paragraphe i
        sum = sum + numerator / denominator #Ajouter le terme i à la somme
    pi = 4 / sum #Calcul du rapport de circonférence
    return pi

#production
print("Ramanujan(1) = " + str(Ramanujan(1)))
print("Ramanujan(2) = " + str(Ramanujan(2)))
print("Ramanujan(3) = " + str(Ramanujan(3)))
print("Ramanujan(4) = " + str(Ramanujan(4)))
print("Ramanujan(5) = " + str(Ramanujan(5)))

Puisque la classe Ramanujan converge très rapidement et que le multiplicateur ($ n! $) Apparaissant dans la formule a une divergence rapide et peut déborder si une valeur élevée est saisie, le terme à additionner est la classe de Bâle ou Beaucoup moins que la classe Leibniz.

Voici les résultats. Même le premier terme correspond à lui seul jusqu'au quatrième chiffre de la minorité, et le troisième et les termes suivants ont la même valeur dans la plage du nombre de chiffres affichés sur l'ordinateur personnel. C'est extrêmement rapide!

Ramanujan(1) = 3.1415850400712375
Ramanujan(2) = 3.141592653597622
Ramanujan(3) = 3.1415926535897936
Ramanujan(4) = 3.1415926535897936
Ramanujan(5) = 3.1415926535897936

Utilisez des nombres aléatoires

Vous pouvez également trouver $ \ pi $ en utilisant un nombre aléatoire. Comme son nom l'indique, un nombre aléatoire est un nombre aléatoire, comme un jet de dés. Cependant, trouver $ \ pi $ en utilisant des nombres aléatoires nécessite un grand nombre d'échantillons ($ \ sim $ millions), et il est trop ennuyeux pour les humains de lancer un million de dés. Le travail de routine gênant est d'introduire un ordinateur pour améliorer l'efficacité, nous allons donc vous présenter ci-dessous comment trouver $ \ pi $ en utilisant des nombres aléatoires!

9. Méthode de Monte Carlo

Considérons un carré $ 1 \ fois 1 $ et un quadrant centré sur l'un de ses sommets. Le rapport de surface entre le carré et le quadrant est de 1 $: \ pi / 4 $. Les points seront créés de manière complètement aléatoire dans cette case. Lorsque le nombre de points augmente, il devient "nombre total de points: nombre de points contenus dans le quadrant $ \ simeq1: \ pi / 4 $". Par exemple, si $ n $ de $ N $ points sont inclus dans le quadrant,

\frac{n}{N}\simeq\frac{\pi}{4} \tag{12}

Ce sera. Utilisez ceci pour trouver le rapport de circonférence.

Mettons-le en œuvre!

import numpy as np

#Méthode de Monte Carlo. Prélevez N échantillons.
def MonteCarlo(N):
    xy = np.random.rand(2, N) #section[0,1)Distribution uniforme des nombres aléatoires(2×N)queue. Chaque colonne correspond aux coordonnées d'un point sur le plan.
    r = np.sum(xy**2, axis = 0) #Calculez la distance depuis l'origine de chaque point d'échantillonnage. Mettez chaque composant au carré et additionnez les éléments dans la même colonne.
    r = r[r<=1] #La distance est égale ou inférieure à 1 (=Extraire uniquement les échantillons (à l'intérieur du quadrant)
    
    n = r.size #Calculez le nombre de points dans le cercle#Calculer le rapport de circonférence
    
    pi = 4 * n / N #Calculer le rapport de circonférence
    return pi

np.random.seed(seed=0) #Paramètre de départ aléatoire (cela entraînera la même sortie à chaque fois)

#production
print("MonteCarlo(100)       = " + str(MonteCarlo(100)))
print("MonteCarlo(1000)      = " + str(MonteCarlo(1000)))
print("MonteCarlo(10000)     = " + str(MonteCarlo(10000)))
print("MonteCarlo(100000)    = " + str(MonteCarlo(100000)))
print("MonteCarlo(1000000)   = " + str(MonteCarlo(1000000)))
print("MonteCarlo(10000000)  = " + str(MonteCarlo(10000000)))

Voici les résultats. En général, l'erreur de valeur due au nombre aléatoire converge de l'ordre de $ 1 / \ sqrt {N} $ pour le nombre d'échantillons $ N $ (relativement lent), donc la précision est assez faible.

MonteCarlo(100)       = 3.24
MonteCarlo(1000)      = 3.068
MonteCarlo(10000)     = 3.1508
MonteCarlo(100000)    = 3.13576
MonteCarlo(1000000)   = 3.140048
MonteCarlo(10000000)  = 3.1424264

10. Aiguille de Buffon

Déposez beaucoup d'aiguilles de longueur $ l $ sur beaucoup de lignes parallèles tracées à des intervalles de $ t $. Soit $ n $ le nombre d'aiguilles $ N $ qui coupent la ligne. Quand le nombre d'aiguilles $ N $ est assez grand

\frac{2lN}{tn}\sim\pi \tag{13}

Est connu pour être. Vous êtes revenu, c'est celui qui dit "Est-ce que $ \ pi $ sort ici!" W C'est une chose apparemment étrange que le rapport de circonférence apparaisse dans la probabilité même si vous venez de faire tomber l'aiguille sur la ligne parallèle. se produire. Cliquez ici pour plus de détails sur les aiguilles Buffon

Mettons-le en œuvre! La distance entre le centre de l'aiguille et la ligne est uniforme à $ 0 \ sim t / 2 $, et l'angle entre l'aiguille et la ligne parallèle est uniforme à $ 0 ^ \ circ \ sim 90 ^ \ circ $. De plus, cette fois, la longueur de l'aiguille est $ l = 2 $ et l'interligne parallèle est $ t = 4 $.

Il y a certaines choses à faire attention lors de l'échantillonnage de l'angle de l'aiguille à partir de nombres aléatoires. Il est nécessaire de convertir la méthode des degrés en méthode des degrés d'arc lors de l'échantillonnage direct de l'angle, mais le «np.radius ()» qui sera utilisé dans ce cas est une fonction qui dépend de la valeur du rapport de circonférence. .. Vous pouvez l'utiliser pour la simulation, mais je me sens personnellement mal à l'aise, je vais donc en imaginer un peu cette fois. ** Échantillonnez les coordonnées d'un point dans le quadrant unitaire et trouvez la valeur de sin à partir de celui-ci **. En limitant la plage de points d'échantillonnage au quadrant unitaire, l'angle entre le point et l'axe $ x $ peut être réduit. Il a une distribution uniforme de 0 $ ^ \ circ \ sim 90 ^ \ circ $.

import numpy as np

#Aiguille de Buffon. Drop N aiguilles.
def Buffon(N):
    n = 0; #Le nombre d'aiguilles qui chevauchent la ligne. Valeur initiale 0.
    for i in range(N): #i est 0 à N-Répétez jusqu'à 1.
        #Échantillonnage de l'angle de l'aiguille. Éliminez la dépendance de valeur de pi en échantillonnant des points dans le cercle unitaire au lieu d'échantillonner directement l'angle.
        r = 2 #La distance depuis l'origine du point d'échantillonnage. Définissez la valeur initiale sur 2 pour exécuter l'instruction while suivante.
        while r > 1: #r<=Répétez l'échantillon jusqu'à ce qu'il atteigne 1.
            dx = np.random.rand() #coordonnée x
            dy = np.random.rand() #coordonnée y
            r = np.sqrt(dx ** 2 + dy ** 2) #Calcul de la distance depuis l'origine
        
        h = 2 * np.random.rand() + dy / r #Calcul de la hauteur (supérieure) de la pointe de la touffe
        if h > 2: #Lorsque la hauteur de la pointe de l'aiguille se termine, la hauteur de la ligne parallèle
            n += 1 #Ajoutez le nombre d'aiguilles qui chevauchent la ligne
    
    pi = N / n #Calcul du rapport de circonférence
    return pi

np.random.seed(seed=0) #Paramètre de départ aléatoire (cela entraînera la même sortie à chaque fois)

#production
print("Buffon(100)        = " + str(Buffon(100)))
print("Buffon(1000)       = " + str(Buffon(1000)))
print("Buffon(10000)      = " + str(Buffon(10000)))
print("Buffon(100000)     = " + str(Buffon(100000)))
print("Buffon(1000000)    = " + str(Buffon(1000000)))
print("Buffon(10000000)   = " + str(Buffon(10000000)))

Génère l'angle des aiguilles $ N $ avec theta = np.radians (rand.rand (N) * 90). Puisque rand.rand () a une distribution uniforme de l'intervalle $ [0, 1) $, le multiplier par 90 donne une distribution uniforme de $ [0, 90) $.

Calculez ensuite les coordonnées $ y $ de la pointe de l'aiguille avec y = 2 * rand.rand (N) + np.sin (thêta). 2 * rand.rand (N) est utilisé pour calculer les coordonnées du centre de l'aiguille, et np.sin (thêta) est utilisé pour calculer la différence de hauteur entre le centre et la pointe de l'aiguille. Le fait que la pointe de l'aiguille coupe ou non la ligne parallèle est déterminé par [y> 2](si $ y> 2 $, elle se coupe, sinon elle ne se coupe pas). Après cela, calculez le nombre d'aiguilles qui se croisent avec y.size, et si vous vous trompez, vous avez terminé.

Voici le résultat de la sortie. Le résultat n'est pas stable. .. .. (Transpiration)

Buffon(100)        = 2.7777777777777777
Buffon(1000)       = 2.881844380403458
Buffon(10000)      = 3.1259768677711786
Buffon(100000)     = 3.11284046692607
Buffon(1000000)    = 3.1381705093564554
Buffon(10000000)   = 3.1422055392056127

Utilisez un algorithme

Un ** algorithme ** est, grosso modo, un ** résumé d'une procédure particulière **. Dans ce qui suit, nous allons vous montrer comment trouver le rapport de circonférence en répétant une procédure spécifique!

11. Algorithme de Gauss-Legendre

L'algorithme de Gauss-Legendre est une méthode de calcul du rapport de circonférence selon la procédure de "répétition des termes d'une séquence de nombres selon l'équation graduelle simultanée" comme suit.

\begin{align}
&a_0=1,\quad b_0=\frac{1}{\sqrt{2}},\quad t_0=\frac{1}{4},\quad p_0=1\\
&a_{n+1}=\frac{a_n+b_n}{2}\\
&b_{n+1}=\sqrt{a_nb_n}\\
&t_{n+1}=t_n-p_n(a_n-a_{n+1})^2\\
&p_{n+1}=2p_n\\
\\
&\frac{a_n+b_n}{4t_n}\to\pi(n\to\infty)
\end{align}
\tag{14}

On sait que cet algorithme double approximativement le nombre de chiffres correspondant à la valeur exacte au fur et à mesure de l'avancement du calcul, ce qui permet d'obtenir le rapport de circonférence facilement et avec une grande précision. Gauss et Legendre, qui ont conçu cet algorithme indépendamment, sont tous deux des superstars dans le monde des mathématiques et de la physique. Cliquez ici pour plus de détails sur l'algorithme de Gauss-Legendre [Cliquez ici pour plus de détails sur Gauss](https://ja.wikipedia.org/wiki/%E3%82%AB%E3%83%BC%E3%83%AB%E3%83%BB%E3%83%95 % E3% 83% AA% E3% 83% BC% E3% 83% 89% E3% 83% AA% E3% 83% 92% E3% 83% BB% E3% 82% AC% E3% 82% A6% E3 % 82% B9) [Cliquez ici pour plus de détails sur Legendre](https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%89%E3%83%AA%E3%82%A2%E3%83%B3 % EF% BC% 9D% E3% 83% 9E% E3% 83% AA% E3% 83% BB% E3% 83% AB% E3% 82% B8% E3% 83% A3% E3% 83% B3% E3 % 83% 89% E3% 83% AB)

Mettons-le en œuvre!

import numpy as np

#Gauss=L'algorithme de Legendre. Répéter N fois
def GaussRegendre(N):
    #Premier mandat
    a = 1.0
    b = np.sqrt(2) / 2
    t = 1 / 4
    p = 1
    
    for i in range(N): #i est 0 à N-Répétez ce qui suit jusqu'à 1
        #Calculez les termes suivants selon la formule graduelle
        a_new = (a + b) / 2
        b_new = np.sqrt(a * b)
        t_new = t - p * (a - a_new)**2
        p_new = 2 * p

        #Remplacer l'ancienne valeur par une nouvelle valeur
        a = a_new
        b = b_new
        t = t_new
        p = p_new
        
    pi = (a + b)**2 / (4 * t) #Calcul du rapport de circonférence
    return pi

#production
print("GaussRegendre(1) = " + str(GaussRegendre(1)))
print("GaussRegendre(2) = " + str(GaussRegendre(2)))
print("GaussRegendre(3) = " + str(GaussRegendre(3)))

Voici les résultats. La première fois va jusqu'au deuxième chiffre de la fraction, la deuxième fois va jusqu'au septième chiffre de la fraction, et la troisième fois jusqu'au dernier chiffre affiché. La convergence est assez rapide!

GaussRegendre(1) = 3.1405792505221686
GaussRegendre(2) = 3.141592646213543
GaussRegendre(3) = 3.141592653589794

Utilisez la physique

Le rapport de circonférence est caché non seulement dans le monde des mathématiques, mais aussi dans le monde naturel. Dans ce qui suit, je vais vous montrer comment calculer le rapport de circonférence en utilisant la physique!

12. Cycle de vibration simple

En physique, les ** vibrations ** et autres mouvements ont été activement étudiés, mais la simple vibration est à la base de tous les mouvements périodiques. La vibration simple est le mouvement lorsque la position $ x $ suit l'équation suivante.

\frac{d^2x}{dt^2}=-\omega^2x \tag{15}

Une équation qui inclut la différenciation d'une fonction, telle que l'équation (15), est appelée une ** équation différentielle **. De nombreuses équations différentielles dans le monde ne peuvent pas être résolues exactement, mais l'équation (15) peut être résolue exactement, et la solution est la suivante.

x=A\sin(\omega t + \phi) \tag{16}

Vous pouvez voir que $ x $ oscille dans le temps car la position $ x $ est représentée par $ \ sin $ en fonction du temps $ t $. $ A $ est l'amplitude de la vibration et $ \ phi $ est une constante appelée phase initiale, qui est liée à la position de l'objet à $ t = 0 $. Et le cycle de cette vibration est

T=\frac{2\pi}{\omega} \tag{17}

Ce sera. Si $ \ omega = 1 $, le demi-cycle de vibration est le rapport de circonférence.

Cette fois, nous calculerons la période de vibration en simulant numériquement l'équation différentielle. La ** méthode Runge ≡ Kutta ** est utilisée pour simuler l'équation différentielle. Puisque l'explication détaillée de la méthode Runge ≡ Kutta est longue, je l'omettrai ici, mais brièvement, «Trouvez la valeur de position et de vitesse dans le futur à partir de la valeur de position et de vitesse à un certain moment selon une certaine procédure. C'est une façon de répéter cela.

\begin{align}
&Intervalle de temps:h,\équation différentielle quadruple:\frac{dx}{dt}=f(x, t)\\
&{k}_1=h\times {f}(x_i, t)\\
&{k}_2=h\times {f}(x_i+\frac{k_1}{2}, t+\frac{h}{2})\\
&{k}_3=h\times {f}(x_i+\frac{k_2}{2}, t+\frac{h}{2})\\
&{k}_4=h\times {f}(x_i+k_3, t+h)\\
\\
&{k}=\frac{{k}_1+2{k}_2+2{k}_3+{k}_4}{6}\\
&x_{i+1}=x_i+{k}
\end{align}
\tag{18}

Cliquez ici pour une explication détaillée de la méthode Runge-Kutta

J'ai également écrit un autre article en utilisant la méthode Runge-Kutta, alors lisez-le si vous le souhaitez! Simulation du chaos dans Unity à l'aide de la méthode Rungekutta

Mettons-le en œuvre! La méthode Runge-Kutta de l'équation (18) est utilisée par défaut pour l'équation différentielle du premier ordre, mais comme l'équation différentielle de l'équation (15) est l'équation différentielle du second ordre, elle est divisée en deux équations différentielles du premier ordre comme suit. Je vais finir.

\begin{align}
&\frac{dx}{dt}=v\\
&\frac{dv}{dt}=-\omega^2x 
\end{align}
\tag{19}

La position initiale et la vitesse initiale sont $ (x_0, v_0) = (1,0) $. Ensuite, le mouvement de l'objet commence à partir du point de vibration le plus élevé. Après cela, la position diminue pendant un moment, atteint le point de vibration le plus bas juste après un demi-cycle, puis la position augmente. Ensuite, en avançant le temps uniquement pendant que la position de l'objet diminue et en s'arrêtant lorsque la position augmente, un temps de demi-cycle (rapport de circonférence ≈) peut être obtenu.

import numpy as np

#Équation différentielle. r:Vecteur résumant la position et la vitesse
def f(r):
    x = r[0] #Retirer la valeur de la position
    v = r[1] #Retirez la valeur de la vitesse

    #Calculez le côté droit de l'équation différentielle
    xdot = v
    vdot = -x

    return np.array([xdot, vdot])

#Runge=Méthode Kutta
def RungeKutta(r, h):
    k1 = h * f(r)
    k2 = h * f(r + k1 / 2)
    k3 = h * f(r + k2 / 2)
    k4 = h * f(r + k3)
    
    k = (k1 + 2 * k2 + 2 * k3 + k4) / 6
    
    return r + k

#Vibration simple. Intervalle de temps h=10^(-N)Exécutez la méthode Runge-Kutta.
def Vibration(N):
    h = 10**(-N) #Calcul de h
    t = 0 #Valeur initiale de l'entier correspondant au temps
    isDecrease = True #Indicateur indiquant si la position diminue
    r = np.array([1.0, 0.0]) #Valeur initiale de la position / vitesse
    x_old = r[0] #Substitution de la valeur initiale à l'ancienne position. Utilisé pour juger de l'augmentation / diminution de la position.

    while isDecrease == True and t * h < 4.0: #Répétez ce qui suit pendant que la position diminue et que le temps est de 4 ou moins
    #※t*h<4.Imposer 0 vous empêche d'entrer dans une boucle infinie

        r = RungeKutta(r, h) #Runge=Mettre à jour la position et la vitesse avec la méthode Kutta
        x_new = r[0] #Nouvelle valeur de position

        if x_old > x_new: #L'ancienne position est plus grande que la nouvelle position (=Si la position diminue)
            x_old = x_new #Remplacer l'ancienne valeur de position
            t += 1 #Avancez le temps
        else : #Autrement
            isDecrease = False #Définissez l'indicateur de diminution sur False → La boucle se termine
    pi = t / 10 ** N
    return pi #Demi-cycle(≒π)rends le

#production
print("Vibration(1) = " + str(Vibration(1)))
print("Vibration(2) = " + str(Vibration(2)))
print("Vibration(3) = " + str(Vibration(3)))
print("Vibration(4) = " + str(Vibration(4)))
print("Vibration(5) = " + str(Vibration(5)))

Voici les résultats. Vous pouvez voir que plus la largeur de $ h $ est petite, plus la précision est élevée. Cependant, cela prend du temps car le nombre de boucles nécessaires augmente en conséquence.

Vibration(1) = 3.1
Vibration(2) = 3.14
Vibration(3) = 3.142
Vibration(4) = 3.1416
Vibration(5) = 3.14159

13. Nombre de collisions entre deux balles

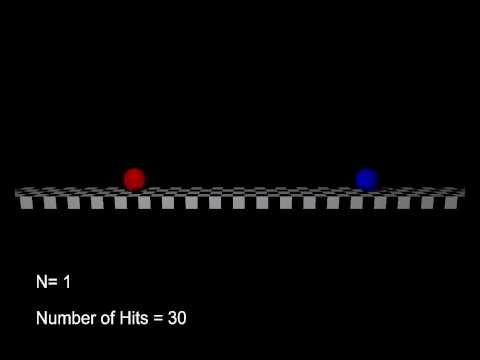
Comme la treizième, c'est-à-dire la dernière méthode, je présenterai la méthode de l'impact pour trouver le rapport de circonférence. On dit que ** le nombre de collisions entre deux boules et un mur est le rapport de circonférence **. Je ne sais pas de quoi vous parlez, alors je posterai une vidéo et l'article original.

Vidéo:

Papier original: PLAYING POOL WITH π (THE NUMBER π FROM A BILLARD POINT OF VIEW)

Préparez deux balles avec un rapport de masse de 1 $: 100 ^ N $, et frappez la balle légère à une vitesse de 1 tout en gardant la balle légère immobile. Préparez un mur devant la boule lumineuse après la collision afin qu'elle rebondisse avec un coefficient de répulsion de 1. Après des collisions répétées, la balle lourde se déplacera dans la direction opposée du mur et la balle légère ne heurtera pas lorsqu'elle ne pourra pas rattraper la balle lourde. Si vous comptez le nombre de fois qu'une balle légère a heurté une balle lourde et un mur jusqu'à présent, ce sera le nombre de chiffres $ N $ du rapport de circonférence.

Mettons-le en œuvre! Tout d'abord, calculez à l'avance le changement de vitesse dû à la collision. La méthode de calcul est une combinaison de la ** loi de conservation de l'exercice ** et de la ** formule de définition du coefficient de répulsion **, qui sont familières en physique au lycée. Supposons que les vitesses des boules légères et lourdes avant la collision soient respectivement $ v et V $, et les vitesses après la collision respectivement $ v'et V'$. Soit le rapport de masse des sphères légères et lourdes $ 1: r $. À ce moment, les deux équations suivantes sont valables avant et après la collision.

\begin{align}
&v+rV=v'+rV'\\
&e=-\frac{v'-V'}{v-V}
\end{align}
\tag{20}

Cette fois, toutes les collisions sont des collisions élastiques, donc $ e = 1 $. Résolution d'équations simultanées pour $ v ', V' $

v'=\frac{(1-r)v+2rV}{1+r},\quad V'=\frac{2v+(r-1)V}{1+r} \tag{21}

Ce sera. Sur cette base, mettons-le en œuvre!

#Collision à deux balles. Trouvez jusqu'au Nième chiffre.
def BallCollision(N):
    v = 0.0  #Vitesse initiale de la boule lumineuse
    V = -1.0 #Vitesse initiale de la balle lourde
    r = 100 ** N #Rapport de masse
    count = 0 #Valeur initiale du nombre de collisions

    while v > V: #Répétez ce qui suit lorsque la vitesse de la balle légère est supérieure à la vitesse de la balle lourde
        v_new = ((1 - r) * v + 2 * r * V) / (r + 1) #Vitesse de la balle légère après collision
        V_new = (2 * v + (r - 1) * V) / (r + 1) #Vitesse de balle élevée après collision
        count += 1 #Ajout du nombre de collisions
        
        if(v_new < 0.0): #Lorsque la vitesse de la boule lumineuse est négative
            v_new = -v_new #La vitesse s'inverse en raison d'une collision avec le mur
            count += 1 #Ajout du nombre de collisions
        
        v = v_new #Remplacement de la vitesse d'une boule légère
        V = V_new #Remplacement de la vitesse d'une balle lourde
    
    pi = count / (10 ** N) #Calcul du rapport de circonférence
    return pi

#production
for i in range(8):
    print("BallCollision(" + str(i) + ") = " + str(BallCollision(i)))

Voici le résultat de l'exécution. Vous voulez vraiment le rapport de circonférence au Nième chiffre! Cependant, la quantité de calcul augmente 100 fois pour augmenter la précision d'un chiffre, donc cela semble être gênant.

BallCollision(0) = 3.0
BallCollision(1) = 3.1
BallCollision(2) = 3.14
BallCollision(3) = 3.141
BallCollision(4) = 3.1415
BallCollision(5) = 3.14159
BallCollision(6) = 3.141592
BallCollision(7) = 3.1415926

J'ai essayé de tout mettre en place dans la classe

Enfin, j'ai rassemblé une classe de toutes les techniques que j'ai implémentées jusqu'à présent! Si vous les collectionnez tous de cette manière, c'est tout un volume. .. .. !!

#Classe Pi_Description de Harem
#Classe Harlem tissée de 13 façons pour trouver le rapport de circonférence.
#Trouvez le rapport de circonférence comme vous le souhaitez!
#* Importer numpy comme np est requis pour utiliser.
#
#Description de la fonction:
#Toutes les fonctions ont une valeur de retour.
#    1.  pi()　: 
#        np.Renvoie la valeur de pi. Aucun argument.
#
#     2.  Arctan()　: 
#        4*np.arctan(1)Renvoie la valeur de. Aucun argument.
#
#    3.  RegularPokygon(N) : 
#Obtenez le rapport de circonférence de l'aire du polygone régulier et renvoyez la valeur. Argument N = nombre de sommets du polygone régulier.
#
#    4.  Rectangle(N) : 
#Obtenez le rapport de circonférence à partir de l'intégration numérique (approximation rectangulaire) et renvoyez la valeur. Argument N = division égale de l'intervalle d'intégration.
#
#    5.  Trapezoid(N) : 
#Obtenez le rapport de circonférence à partir de l'intégration numérique (approximation trapoïdale) et renvoyez la valeur. Argument N = division égale de l'intervalle d'intégration.
#
#    6.  Basel(N) : 
#Calculez le rapport de circonférence de la classe de Bâle et renvoyez la valeur. Argument N = nombre de termes qui prennent la somme.
#
#    7.  Leibniz(N) : 
#Trouvez le rapport de circonférence de la classe Leibniz et renvoyez la valeur. Argument N = nombre de termes qui prennent la somme.
#
#    8.  Ramanujan(N) : 
#Calculez le rapport de circonférence de la classe Ramanujan et renvoyez la valeur. Argument N = nombre de termes qui prennent la somme.
#
#    9.  MonteCarlo(N) : 
#Trouvez le rapport de circonférence à partir du produit Monte Carlo du quadrant et renvoyez la valeur. Argument N = nombre d'échantillons.
#
#    10. Buffon(N) : 
#Obtenez le rapport de circonférence de la simulation de l'aiguille de Buffon et renvoyez la valeur. Argument N = nombre d'échantillons.
#
#    11. GaussRegendre(N) : 
#Gauss=Trouvez le rapport de circonférence à partir de l'algorithme de Legendre et renvoyez la valeur. Argument N = nombre d'itérations de l'algorithme.
#
#    12. Vibration(N) : 
#Obtenez le rapport de circonférence à partir de la simulation d'une vibration simple et renvoyez la valeur. Argument N = Une variable qui détermine la largeur du pas de temps h. h=10^(-N)
#
#    13. BallCollision(N) : 
#Le rapport de circonférence est obtenu à partir de la simulation de la collision de deux billes, et la valeur est renvoyée. Argument N = nombre de chiffres à rechercher.

import numpy as np

#Définition de classe
class Pi_Harem():
    #Fonctions de base de Numpy
    # 1.Valeur exacte de π(numpy.Utiliser pi)
    def pi(self):
        return np.pi
    
    # 2.Fonction inverse du bronzage
    def Arctan(self):
        return 4 * np.arctan(1)
    
    #zone
    # 3.Approximation polygonale
    def RegularPolygon(self, N):
        theta = np.radians(360 / N)
        pi = N * np.sin(theta) / 2
        
        return pi
    
    # 4.Approximation rectangle
    def Rectangle(self, N):
        x = np.arange(N) / N
        y = np.sqrt(1 - x**2)
        pi = 4 * np.sum(y) / N
        
        return pi
    
    # 5.Approximation trapézoïdale
    def Trapezoid(self, N):
        x = np.arange(N + 1) / N
        y = np.sqrt(1 - x**2)
        z = (y[0:N] + y[1:N+1]) / 2    
        pi = 4 * np.sum(z) / N
        
        return pi
    
    #séries
    # 6.Classe de Bâle
    def Basel(self, N):
        x = np.arange(1, N + 1)
        pi = np.sqrt(6 * np.sum(1 / x**2))
        
        return pi

    # 7.Classe Leibniz
    def Leibniz(self, N):
        x = np.arange(1, N + 1)
        y = 2 * x - 1
        pi = 4 * np.dot(1 / y, (-1)**(x - 1))
        
        return pi
    
    # 8.Classe Ramanujan
    def Ramanujan(self, N):
        sum = 0.0
        
        for i in range(N):
            numerator = ((-1)**i) * np.math.factorial(4 * i) * (1123 + 21460 * i)
            denominator = (882**(2 * i + 1)) * ((4**i) * np.math.factorial(i))**4
            sum = sum + np.sum(numerator / denominator)
            
        pi = 4 / sum
        
        return pi
    
    #nombre aléatoire
    # 9.Méthode de Monte Carlo
    def MonteCarlo(self, N):
        xy = np.random.rand(2, N)
        r = np.sum(xy**2, axis = 0)
        r = r[r<=1]
        n = r.size
        
        pi = 4 * n / N
        
        return pi
    
    # 10.Aiguille de Buffon
    def Buffon(self, N):
        n = 0;
        for i in range(N):
            r = 2
            while r > 1:
                dx = np.random.rand()
                dy = np.random.rand()
                r = np.sqrt(dx ** 2 + dy ** 2)
        
            h = 2 * np.random.rand() + dy / r
            if h > 2:
                n += 1
    
        pi = N / n
        return pi
    
    #algorithme
    # 11.Gauss=Algorithme de Legendre
    def GaussRegendre(self, N):
        a = 1.0
        b = np.sqrt(2) / 2
        t = 1 / 4
        p = 1
        
        for i in range(N):
            a_new = (a + b) / 2
            b_new = np.sqrt(a * b)
            t_new = t - p * (a - a_new)**2
            p_new = 2 * p
            
            a = a_new
            b = b_new
            t = t_new
            p = p_new
        
        pi = (a + b)**2 / (4 * t)
        return(pi)
    
    #La physique
    # 12.Vibration simple
    #Équation différentielle(Fonction privée)
    def __f(self, r):
        x = r[0]
        v = r[1]
        xdot = v
        vdot = -x
        return np.array([xdot, vdot])
    
    #Méthode Rungekutta(Fonction privée)
    def __RungeKutta(self, r, h):
        k1 = h * self.__f(r)
        k2 = h * self.__f(r + k1 / 2)
        k3 = h * self.__f(r + k2 / 2)
        k4 = h * self.__f(r + k3)
    
        k = (k1 + 2 * k2 + 2 * k3 + k4) / 6
    
        return r + k
    
    #Calcul du cycle
    def Vibration(self, N):
        h = 10 ** (-N)
        t = 0
        isDecrease = True
        r = np.array([1.0, 0.0])
        x_old = r[0]
        
        while isDecrease == True and t * h < 4.0:
            r = RungeKutta(r, h)
            x_new = r[0]

            if x_old > x_new:
                x_old = x_new
                t += 1
            else :
                isDecrease = False
            
        pi = t / 10 ** (N)
        return pi
    
    # 13.Collision à deux balles
    def BallCollision(self, N):
        v = 0.0
        V = -1.0
        r = 100 ** N
        count = 0
        while v > V:
            v_new = ((1 - r) * v + 2 * r * V) / (r + 1)
            V_new = (2 * v + (r - 1) * V) / (r + 1)
            count += 1
        
            if(v_new < 0.0):
                v_new = -v_new
                count += 1
        
            v = v_new
            V = V_new
    
        pi = count / (10 ** N)
        return pi
    
    #c'est tout

Pour les notebooks jupyter, vous pouvez exécuter le code ci-dessus dans une cellule, puis exécuter le code suivant dans une autre cellule (si vous utilisez la fonction Basel () dans la classe).

pi_harem = Pi_Harem() #Pi_Harem()La variable pi_Assigner au harem (ne le faire qu'une seule fois)
pi = pi_harem.Basel(1000) #La fonction Barsel dans la classe à la variable pi(1000)Remplacez la valeur de
print(pi) #production

Résumé

Comment était-ce? Cette fois, j'ai traité de 13 façons de calculer le rapport de circonférence en Python. C'était beaucoup de volume et ça a pris beaucoup de temps à écrire (sueur)

Il y avait de nombreuses méthodes royales, non triviales et originales! Je ne me suis jamais lassé de voir toutes les méthodes et cela a été difficile pour moi personnellement. .. ..

Je continuerai à publier des articles portant sur la physique et la programmation. ** Si vous avez un thème que vous aimeriez que nous abordions, laissez-le dans les commentaires! ** **