[PYTHON] J'ai essayé de simuler l'optimisation des publicités à l'aide de l'algorithme Bandit
introduction
Le but de cet article est de comprendre les caractéristiques de chaque méthode de l'algorithme Bandit en effectuant des simulations en supposant des cas d'utilisation réels.
Le post Qiita suivant est souvent mentionné en japonais à propos de l'algorithme de bandit. http://qiita.com/yuku_t/items/6844aac6008911401b19
Les matériaux suivants présentent également les détails et les caractéristiques de chaque méthode et des simulations simples. http://www.slideshare.net/greenmidori83/ss-28443892
Étant donné que l'introduction de la méthode dans le matériel ci-dessus est très facile à comprendre, cette entrée n'introduit pas spécifiquement la méthode.
Cas d'utilisation supposé
Vous diffusez actuellement une annonce qui a été diffusée 10 000 fois et dont le taux de clics est de 1,2% pour 60 yens par clic. J'ai décidé d'essayer différents modèles de bannières pour trouver plus d'annonces cliquées. J'ai fait 10 nouvelles bannières. Supposons que deux de ces bannières aient un meilleur taux de clics que l'actuelle, que trois soient identiques à l'annonce actuelle et que les cinq autres présentent un taux de clics inférieur à l'actuel.
--1,3% 2 pièces -1,2% est égal à 3 -1,1% est 3 --Deux 1,0%
Pourquoi voulez-vous augmenter le taux de clics
Cela n'a rien à voir avec le sujet principal, mais pourquoi voulez-vous augmenter le taux de clics et pourquoi est-il judicieux de faire une expérience alors que le taux de clics n'augmente que de 0,1%? Pensons à ça. Vous pourriez penser qu'augmenter le taux de clics n'a pas beaucoup de sens, car le montant que vous payez pour chaque clic ne change pas. Cependant, du point de vue de l'annonceur, placer une annonce avec un faible taux de clics réduira les ventes, donc si le taux de clics est faible, il sera difficile d'afficher l'annonce. À cette époque, un index appelé eCPM est souvent utilisé. L'eCPM est un indice des ventes pouvant être réalisées en affichant la publicité 1 000 fois. Taux de clics * 1000 * Calculé par le coût par clic. Les annonces avec un EPCM élevé sont plus susceptibles d'être affichées. Par conséquent, l'augmentation du taux de clics permettra à de nombreux utilisateurs d'être dirigés vers votre page de destination au même coût par clic. Par exemple, dans ce cas, le taux de clic est de 1,2% et le coût par clic est de 60 yens, donc l'eCPM est de 720 yens. Si le taux de clics augmente de 0,1%, l'eCPM sera de 780 yens. À ce moment-là, même si le coût par clic est de 56 yens, l'eCPM sera de 726 yens, ce qui signifie que si le taux de clic augmente de 0,1%, le prix unitaire pour obtenir le même montant de guidage vers la page de destination peut être réduit de 4 yens. Par exemple, si un produit est acheté sur cette page de destination à 1%, le coût de vente d'un produit sera réduit de 400 yens. Au cas par cas, augmenter les taux de clics de cette manière est un facteur très important dans la vente d'objets via la publicité Web.
simulation
La mise en œuvre a été empruntée à la suivante
https://github.com/johnmyleswhite/BanditsBook
Jetons un coup d'œil à Epsilon Greedy, Softmax, UCB
Epsilon Greedy
Epsilon Greedy est une méthode pour choisir une option que vous ne pensez pas être la meilleure maintenant avec une certaine probabilité. Tout d'abord, je vais essayer de rechercher à environ 10%. Essayons 1000 fois.
execfile("core.py")
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
algo1 = EpsilonGreedy(0.1, counts, values)
for t in range(1000):
chosen_arm = algo1.select_arm()
reward = arms[chosen_arm].draw()
algo1.update(chosen_arm, reward)
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre d'essais | 77 | 109 | 82 | 38 | 38 | 50 | 264 | 205 | 49 | 47 | 41 |
| Probabilité d'évaluation | 1.2% | 0.9% | 3.7% | 0% | 0% | 2.0% | 2.3% | 2.0% | 0% | 0% | 0% |
Avec 11 choix, vous ne pouvez pas le dire du tout dans environ 1000 essais. Ce résultat variera considérablement de temps en temps car il dépend également de la génération de nombres aléatoires.
Et si vous essayez 10 000 fois?
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre d'essais | 1,321 | 824 | 481 | 623 | 1,827 | 562 | 1,026 | 968 | 452 | 1206 | 710 |
| Probabilité d'évaluation | 1.2% | 1.2% | 0.6% | 1.2% | 1.3% | 0.7% | 1.2% | 1.1% | 0.9% | 1.2% | 1.3% |
Ce n'est pas un résultat terrible, mais il est difficile de dire que c'est un bon résultat.
Ensuite, essayez d'augmenter le degré de recherche à environ 50%. 1000 premières fois
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre d'essais | 239 | 70 | 40 | 72 | 37 | 44 | 137 | 45 | 52 | 211 | 53 |
| Probabilité d'évaluation | 1.2% | 1.4% | 0% | 1.4% | 0% | 0% | 1.5% | 0% | 0% | 1.9% | 0% |
Est-ce un état où epsilon est recherché uniformément par rapport à 10%? 10 000 fois suivantes
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre d'essais | 1,035 | 1,915 | 8,120 | 1,046 | 1,026 | 1,104 | 885 | 899 | 1,007 | 1,354 | 1,609 |
| Probabilité d'évaluation | 1.2% | 1.3% | 1.3% | 1.1% | 1.1% | 1.0% | 0.9% | 1.1% | 1.1% | 0.7% | 1.2% |
J'ai pu trouver la meilleure bannière, mais c'est arrivé. On constate que les autres bannières sont essayées de manière égale par rapport à 10%. Puisqu'il y a une grande variation d'un essai à l'autre, évaluons par la moyenne des epcm répétés plusieurs fois.
eCPM demande
def calc_ecpm(algo):
total = sum(algo.counts) - 10000
ecpm = 0.0
for idx, count in enumerate(algo.counts):
if idx == 0:
count -= 10000
if count == 0:
continue
ecpm += 1000 * 60 * algo.values[idx] * float(count)/total
return ecpm
Maintenant, définissez les paramètres par incréments de 0,1 à 0,9 de 0,1, et l'ecpm ressemblera à ceci lorsque le bandit avec 10000 essais est exécuté 1000 fois pour chaque paramètre.
def run_eg(ep, counts, values, arms):
algo = EpsilonGreedy(ep, counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_ecpm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for ep in xrange(1, 10):
print ep * 0.1
for _ in xrange(10000):
data.append((ep*0.1, run_eg(ep*0.1, counts, values, arms)))
return pandas.DataFrame(data, columns=['ep', 'epcm'])
result = run()
result.boxplot(by="ep")

Si l'epsilon est petit, il variera considérablement. Cependant, il semble que plus le résultat est grand, plus le résultat est petit. Il a également été constaté qu'il dépasse fondamentalement l'ECPM d'origine de 720. Il semble que même un algorithme aussi simple puisse donner des résultats suffisamment utiles.
SoftMax
Le paramètre de Softmax est tau. Plus il est petit, plus vous faites confiance à la valeur déjà calculée. Cela essaiera les paramètres de 2 ^ -5 à 2 ^ 5 1000 fois chacun.
def run_sm(tau, counts, values, arms):
algo = Softmax(tau, counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_epcm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for i in xrange(10):
tau = 2**(i - 5)
print tau
for _ in xrange(10000):
data.append((tau, run_sm(tau, counts, values, arms)))
return pandas.DataFrame(data, columns=['tau', 'epcm'])
result = run()
result.boxplot(by="tau")

J'ai eu de pires résultats que d'habitude! C'est parce que softmax continue toujours à tirer de mauvaises valeurs avec une certaine probabilité. Lors de l'utilisation de softmax, il semble nécessaire de couper rapidement les mauvaises options.
UCB
Enfin UCB UCB n'a pas de paramètres donc je vais le faire tel quel
def run_ucb(counts, values, arms):
algo = UCB1(counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_epcm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for _ in xrange(10000):
data.append(run_ucb(counts, values, arms))
return pandas.DataFrame(data, columns=['epcm'])
result = run()
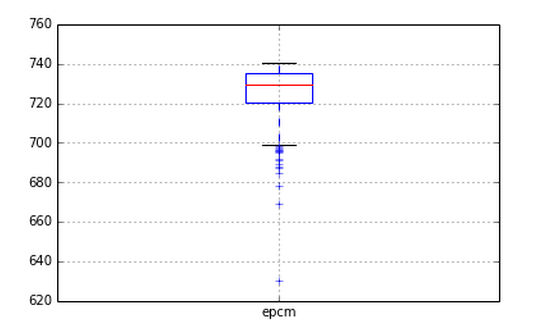
On voit que la recherche peut être effectuée sans abaisser l'epcm. Il sera inférieur à Epsilon Greedy, mais cette zone sera probablement un compromis avec la vitesse de recherche.
Comparaison et prise en compte de chaque méthode
Je veux l'écrire plus tard. Je veux aussi le comparer avec le test A / B.
Résumé
Je ne peux pas dire quelle méthode est la meilleure dans cette entrée. Je pense qu'il y a beaucoup de choses à penser si nous voulons poursuivre plus de cas d'utilisation, J'espère que cela mènera à comprendre en quelque sorte ce qu'est l'algorithme de bandit.
L'algorithme de bandit se caractérise par sa capacité à rechercher tout en utilisant les actifs de données obtenus jusqu'à présent. Je pense que l'un des avantages est que l'exploration peut réduire le risque de mise en danger de l'entreprise en abaissant des indicateurs importants tels que l'eCPM. Par conséquent, je voulais vérifier à l'avance quel type d'utilité peut être obtenu lorsqu'il y a des actifs de données, plutôt que de faire le bon choix, j'ai donc essayé ce type de simulation. Nous espérons que vous le trouverez utile. Et si vous avez des opinions, n'hésitez pas à commenter!
Recommended Posts