Défis de Coursera Machine Learning en Python: ex5 (ajustement des paramètres de régularisation)

Une série qui implémente des tâches de programmation Matlab / Octave dans la classe d'apprentissage automatique de Coursera (professeur Andrew Ng) en Python. Le concept reste le même:

• Plutôt que de reproduire le code de la tâche tel quel, implémentez-le aussi efficacement que possible en utilisant une bibliothèque Python telle que scicit-learn.

Cette semaine (semaine 6) est intitulée «Conseils pour l'application de l'apprentissage automatique» et au lieu d'apprendre un nouveau modèle d'apprentissage, vous apprendrez à régler les paramètres du modèle et à vérifier les performances du modèle. En consacrant une semaine à ce thème, je pense que la particularité de ce cours ** "pratique plutôt que théoriquement biaisé" ** apparaît.

Voici un aperçu rapide de la façon de régler votre modèle:

• S'il y a des données, divisez-les en données d'entraînement, données de validation croisée et données de test. La recommandation du Dr Andrew est un ratio de 6: 2: 2. --Apprentissage avec différents modèles et paramètres à l'aide de données d'entraînement.
• Test croisé pour déterminer quel modèle et quels paramètres sont bons. À ce moment-là, dessinez une courbe d'apprentissage pour déterminer.
• Mesurer les performances du dernier modèle déterminé avec des données de test.

Les tâches de programmation suivront également cette procédure.

Tout d'abord, lisez les données

Vous pouvez charger des données au format matlab .mat avec scio.loadmat () de scipy.

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import linear_model, preprocessing

# scipy.io.loadmat()Lire les données Matlab en utilisant
data = scio.loadmat('ex5data1.mat')
X = data['X']
Xval = data['Xval']
Xtest = data['Xtest']
y = data['y']
yval = data['yval']
ytest = data['ytest']

Il semble que ces données utilisent le niveau d'eau de X = barrage pour prédire la quantité d'eau s'écoulant de y = barrage.

Essayez d'abord la régression linéaire

Pour le moment, je vais faire une régression linéaire et la tracer.

model = linear_model.Ridge(alpha=0.0)
model.fit(X,y)

px = np.array(np.linspace(np.min(X),np.max(X),100)).reshape(-1,1)
py = model.predict(px)
plt.plot(px, py)
plt.scatter(X,y)
plt.show()

Vous pouvez utiliser le modèle linear_model.LinearRegression () que vous utilisez toujours, mais j'utilise le modèle Ridge () car j'ajouterai un terme de régularisation plus tard. Dans ce modèle, vous pouvez spécifier la force de la régularisation avec le paramètre ʻalpha, mais si vous définissez ʻalpha = 0.0, il n'y a pas de régularisation, ce qui est identique au modèleLinearRegression ().

Cliquez ici pour les résultats.

Comme vous pouvez le voir, les données ne correspondent pas bien aux lignes droites.

Essayez toujours de dessiner une courbe d'apprentissage avec régression linéaire

Tout en sachant qu'une ligne droite ne s'applique pas, essayez de dessiner une courbe d'apprentissage en modifiant le nombre de données d'entraînement. Effectuez une régression linéaire avec 1 à 12 données d'entraînement et tracez les erreurs pour les données d'entraînement et les erreurs pour les données de validation croisée. «Erreur» est l'erreur quadratique qui peut être calculée par la formule suivante. $ \frac{1}{2m} \sum (h_\theta(x^{(i)}) - y^{(i)})^2 $ Cliquez-ici pour le code.

#Essayez de dessiner une courbe d'apprentissage avec régression linéaire
error_train = np.zeros(11)
error_val = np.zeros(11)
model = linear_model.Ridge(alpha=0.0)
for i in range(1,12):
    #Effectuer une régression avec seulement i sous-ensembles de données d'entraînement
    model.fit( X[0:i], y[0:i] )
    #Calculer les erreurs dans i sous-ensembles de ces données d'entraînement
    error_train[i-1] = sum( (y[0:i] - model.predict(X[0:i]))**2 ) / (2*i)
    #Calculer l'erreur dans les données pour le test croisé
    error_val[i-1] = sum( (yval - model.predict(Xval) )**2 ) / (2*yval.size)
    
px = np.arange(1,12)
plt.plot(px, error_train, label="Train")
plt.plot(px, error_val, label="Cross Validation")
plt.xlabel("Number of training examples")
plt.ylabel("Error")
plt.legend()
plt.show()

Le résultat est comme ça.

Même si les données d'entraînement sont augmentées à 12 (toutes), l'erreur ne diminue pas pour les données de train et les données de validation croisée. Comme ce n'est pas le cas avec le modèle de régression linéaire, l'étape suivante consiste à essayer l'ajustement polymorphe.

Raccord polygonal

L'hypothèse de régression linéaire implémentée ci-dessus est $ h_\theta(x) = \theta_0 + \theta_1x$ Cependant, l'ajustement polynomial ajoute ici le terme d'échelle $ x . $ h_\theta(x) = \theta_0 + \theta_1x + \theta_2x^2 + \theta_3x^3 + ... + \theta_px^p$$ C'est une expression comme. Plus précisément, la valeur numérique du produit du montant de la fonction $ x $ est calculée à l'avance, et elle est utilisée comme un nouveau montant de fonction de $ x_1, x_2, x_3 ... , et ces données sont utilisées. $ h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + ... + \theta_px_p$$ Apprenez avec le modèle de régression linéaire représenté par.

Dans scikit-learn, il existe une classe appelée sklearn.preprocessing.PolynomialFeatures qui calcule et crée les caractéristiques de ce polynôme, nous allons donc l'utiliser. Cliquez-ici pour le code.

#Calculez le multiplicateur de X et de la nouvelle fonctionnalité X_Que ce soit poly
#X est une matrice m x 1, X_poly est une matrice m x 8
poly = preprocessing.PolynomialFeatures(degree=8, include_bias=False)
X_poly = poly.fit_transform(X)

# X_Régression linéaire utilisant poly
model = linear_model.Ridge(alpha=0.0)
model.fit(X_poly,y)

#terrain
px = np.array(np.linspace(np.min(X)-10,np.max(X)+10,100)).reshape(-1,1)
#Ce modèle est x_Puisque poly est accepté comme entrée, x pour le traçage est également développé sous forme d'échelle.
px_poly = poly.fit_transform(px)
py = model.predict(px_poly)
plt.plot(px, py)
plt.scatter(X, y)
plt.show()

Cliquez ici pour les résultats de l'ajustement.

L'ajustement avec un polypole d'ordre 8 s'applique à toutes les données d'entraînement. Cependant, il s'agit d'un surentraînement et peut être un modèle peu prévisible pour les nouvelles données. Cette fois, tout en vérifiant ce modèle avec les données de test croisé, nous ajusterons les paramètres de régularisation en insérant le terme de régularisation.

Réglage des paramètres de régularisation

En incluant le terme de régularisation, la fonction de coût de la régression linéaire $ J = \ frac {1} {2m} \ sum_ {i = 1} ^ m (h_ \ theta (x ^ {(i)}) --y ^ {(i)}) ^ 2 + \ frac {\ Cela ressemble à lambda} {2m} \ sum_ {j = 1} ^ n \ theta_j ^ 2 $. Le deuxième terme est le terme de régularisation, qui peut éviter le surapprentissage en pénalisant les valeurs des paramètres qui s'écartent de 0. Cette forme de régularisation est appelée régularisation L2, régression Ridge, etc.

$ \ Lambda $ dans la molécule du deuxième terme est un paramètre qui ajuste la force de la régularisation. Comme nous l'avons vu ci-dessus, cela correspond au paramètre ʻalpha dans linear_model.Ridge () `. Comme avec Coursera, changez ce paramètre en 0,001, 0,003, 0,01, 0,03, 0,1, 0,3, 1, 3, 10 et tracez la courbe d'apprentissage pour voir quel $ \ lambda $ vous convient.

Cliquez-ici pour le code.

#Calculez le multiplicateur de X et de la nouvelle fonctionnalité X_Que ce soit poly
#X est une matrice m x 1, X_poly est une matrice m x 8
poly = preprocessing.PolynomialFeatures(degree=8, include_bias=False)
X_poly = poly.fit_transform(X) #Données d'entraînement
Xval_poly = poly.fit_transform(Xval) #Données de validation croisée

#Essayez de dessiner une courbe d'apprentissage en modifiant λ
error_train = np.zeros(9)
error_val = np.zeros(9)
lambda_values = np.array([0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1.0, 3.0, 10.0])
for i in range(0,9):
    # X_Régression linéaire utilisant poly
    model = linear_model.Ridge(alpha=lambda_values[i]/10, normalize=True ) #Changer le paramètre de régularisation alpha
    model.fit(X_poly,y)
    #Calculer les erreurs dans les données d'entraînement (avec terme de régularisation)
    error_train[i] = sum( (y - model.predict(X_poly))**2 ) / (2*y.size) + sum(sum( model.coef_**2 )) * lambda_values[i]/(2*y.size)
    #Calculer l'erreur dans les données pour le test croisé (avec terme de régularisation)
    error_val[i] = sum( (yval - model.predict(Xval_poly) )**2 ) / (2*yval.size) + sum(sum( model.coef_**2 ))* lambda_values[i]/(2*yval.size)

px = lambda_values
plt.plot(px, error_train, label="Train")
plt.plot(px, error_val, label="Cross Validation")
plt.xlabel("Lambda")
plt.ylabel("Error")
plt.legend()
plt.show()

Le tracé ressemble à ceci, et le résultat est que $ \ lambda = 3 $, qui a la plus petite valeur d'erreur dans le test croisé, est bon.

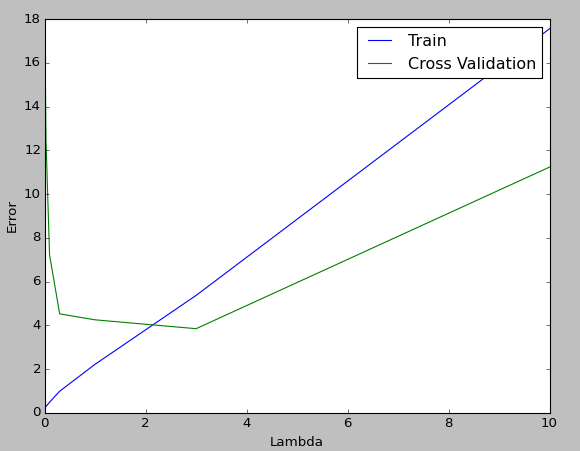
en conclusion

sklearn.linear_model.Ridge () a aussi un modèle appelésklearn.linear_model.RidgeCV ()pour le test croisé, et il semble qu'il calculera le nombre optimal de ʻalpha` ensemble une fois entraîné.

Les références

• Explication de scikit-learn
• Effet de la régularisation L1 et de la régularisation L2 dans le modèle de régression