Jouez des nombres manuscrits avec python, partie 2 (identifier)
Identifier les données numériques manuscrites
Dans l'article précédent, j'ai lu et imaginé des données numériques manuscrites, puis j'ai examiné la corrélation, mais cette fois, j'aimerais identifier le nombre.
Puisqu'il s'agit d'un numéro d'identification manuscrit, il identifie à laquelle des 10 classes de 0 à 9 correspondent les données données. Alors d'abord,
C = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}
Définissez 10 classes de.
L'une des méthodes d'apprentissage automatique est appelée «apprentissage supervisé», et ce modèle est utilisé. Avec un enseignant, en accumulant un certain nombre de données de réponses correctes à l'avance et en les analysant, un discriminateur nécessaire à l'identification est créé, et les données que vous voulez réellement identifier sont entrées dans ce discriminateur pour identification. C'est le chemin. Ces données préparées à l'avance sont appelées données enseignants.
Modèle correspondant à
Cette fois, je voudrais essayer de reconnaître les nombres en utilisant la méthode de correspondance de modèle. Définissez la valeur représentative de chaque étiquette (ici, les nombres de 0 à 9) et faites un classificateur. Cette fois, la valeur moyenne des données de l'enseignant est utilisée comme valeur représentative. Nous allons calculer la distance entre cette valeur représentative et les données transmises à identifier et dire qu'elle appartient à la classe de la valeur représentative avec la distance la plus courte.
La dernière fois, je traitais des données numériques manuscrites de "train_small.csv", mais cette fois, il s'agit de la version complète des données "train.csv" ( 42 000 données) seront utilisées comme données sur les enseignants pour l'apprentissage. Puisque les données numériques utilisent des données d'image 28x28, elles peuvent être représentées par un vecteur de 784 dimensions, et chacune des données d'enseignant est
y_i= (y_1, y_2,...,y_{784}) (i=0,1,...,9)
Il est exprimé comme. $ i $ est une classe pour chaque nombre.
Ici, la valeur représentative est décrite comme $ \ hat {y} _i $.
Par exemple, la valeur représentative d'une classe avec le numéro 8 est $ \ hat {y} _8 $. Les valeurs représentatives sont les suivantes en moyenne.
$ n_i $ est le nombre de données d'enseignant pour chaque nombre.
\hat{y}_i = \frac{1}{n_i}\sum_{j=1}^{n_i} y_j
Maintenant, si la donnée cible à identifier est exprimée comme $ x_j $
x_j= (x_1, x_2,...,x_{784})
Comme il est également représenté par un vecteur de 784 dimensions, comme discriminateur
{\rm argmin}_i{({\rm distance}_i)} = {\rm argmin}_i{(\|\hat{y}_i - x_j\|)}
Est utilisé.
Dérivation et affichage de valeurs représentatives
Je vais en fait calculer. Importez d'abord les bibliothèques requises.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from collections import defaultdict
Définissez une fonction comme un utilitaire. Le premier chiffre est l'étiquette, et ce qui suit sont les données, donc la fonction add_image () qui le divise et le classe par classe, la fonction count_label () qui compte le nombre de chaque étiquette et plot_digits () pour le dessin graphique.
image_dict = dict()
def add_image(label, image_vector):
vec = np.array(image_vector)
if label in image_dict:
image_dict[label] += vec
else:
image_dict[label] = vec
return image_dict
label_dd = defaultdict(int)
def count_label(data):
for d in data:
label_dd[d[0]] += 1
return label_dd
def plot_digits(X, Y, Z, size_x, size_y, counter, title):
plt.subplot(size_x, size_y, counter)
plt.title(title)
plt.xlim(0,27)
plt.ylim(0,27)
plt.pcolor(X, Y, Z)
plt.gray()
plt.tick_params(labelbottom="off")
plt.tick_params(labelleft="off")
Tout d'abord, créez une valeur représentative $ \ hat {y} _i $ et affichez-la sous forme d'image.
size = 28
raw_data= np.loadtxt('train_master.csv',delimiter=',',skiprows=1)
# draw digit images
plt.figure(figsize=(11, 6))
# data aggregation
for i in range(len(raw_data)):
add_image(raw_data[i,0],raw_data[i,1:785])
count_dict = count_label(raw_data)
standardized_digit_dict = dict() #Objet de dictionnaire qui stocke des valeurs représentatives
count = 0
for key in image_dict.keys():
count += 1
X, Y = np.meshgrid(range(size),range(size))
num = label_dd[key]
Z = image_dict[key].reshape(size,size)/num
Z = Z[::-1,:]
standardized_digit_dict[int(key)] = Z
plot_digits(X, Y, standardized_digit_dict[int(key)], 2, 5, count, "")
plt.show()

La dernière fois, lorsque j'ai visualisé des données individuelles et les ai affichées, il y en avait qui ne semblaient pas être des chiffres, mais si vous superposez beaucoup de données et prenez la moyenne, de beaux chiffres sortiront. Celle-ci sera utilisée comme valeur représentative pour chaque classe, et elle sera comparée aux données à identifier.
Effectuer l'identification: essayez d'abord
C'est finalement l'exécution de l'identification. Tout d'abord, je voudrais voir quelle est la distance entre une donnée cible d'identification et la valeur représentative de chaque classe afin de saisir l'image. Les données de la cible d'identification seront téléchargées depuis Kaggle. Utilisez test.csv sur la page de données (https://www.kaggle.com/c/digit-recognizer/data). Puisqu'il y en a quelques-uns, nous préparons les données extraites des 200 premiers (test_small.csv)
test_data= np.loadtxt('test_small.csv',delimiter=',',skiprows=1)
# compare 1 tested digit vs average digits with norm
plt.figure(figsize=(10, 9))
for i in range(1): #Essayez seulement le premier
result_dict = defaultdict(float)
X, Y = np.meshgrid(range(size),range(size))
Z = test_data[i].reshape(size,size)
Z = Z[::-1,:]
flat_Z = Z.flatten()
plot_digits(X, Y, Z, 3, 4, 1, "tested")
count = 0
for key in standardized_digit_dict.keys():
count += 1
X1 = standardized_digit_dict[key]
flat_X1 = standardized_digit_dict[key].flatten()
norm = np.linalg.norm(flat_X1 - flat_Z) #Dérivation de la distance entre chaque valeur représentative et les données à identifier
plot_digits(X, Y, X1, 3, 4, (1+count), "d=%.3f"% norm)
plt.show()
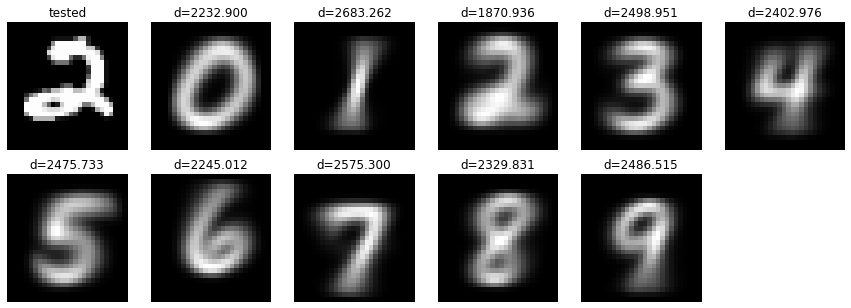
Les données cibles d'identification sont "2", mais qu'en est-il du résultat? La distance est affichée au-dessus de chaque image. En regardant ce nombre, d = 1870,936 au-dessus de "2" est le plus petit! L'identification est réussie! : détendu:
Exécution de l'identification: Résultat d'identification de 200 données
Identifions maintenant 200 éléments de données et voyons à quel point ils sont précis.
# recognize digits
plt.figure(figsize=(15, 130))
for i in range(len(test_data)):
result_dict = defaultdict(float)
X, Y = np.meshgrid(range(size),range(size))
tested = test_data[i].reshape(size,size)
tested = tested[::-1,:]
flat_tested = tested.flatten()
norm_list=[]
count = 0
for key in standardized_digit_dict.keys():
count += 1
sdd = standardized_digit_dict[key]
flat_sdd = sdd.flatten()
norm = np.linalg.norm(flat_sdd - flat_tested)
norm_list.append((key, norm))
norm_list = np.array(norm_list)
min_result = norm_list[np.argmin(norm_list[:,1])]
plot_digits(X, Y, tested, 40, 5, i+1, "l=%d, n=%d" % (min_result[0], min_result[1]))
plt.show()
J'ai essayé d'appliquer 200 données cibles d'identification à cette machine d'identification, et le taux de réponse correct était de 80% (160/200), ce qui était un mauvais résultat! : smile: N'est-ce pas un bon résultat pour la méthode simple de mesurer simplement la distance par rapport à la valeur moyenne? Voir la figure ci-dessous pour les données détaillées réelles.

Lors de l'analyse des cas qui n'ont pas pu être identifiés, il était particulièrement difficile de faire la distinction entre 4 et 9, et 6 erreurs d'identification se sont produites. Ensuite, 1-7, 1-8, 3-5, 3-8, 3-9, 8-9 sont respectivement trois erreurs. Après tout, les chiffres se ressemblent un peu.
** Résumé des erreurs d'identification **
| combination of label | count |
|---|---|
| 4-9 | 6 |
| 1-7 | 3 |
| 1-8 | 3 |
| 3-5 | 3 |
| 3-8 | 3 |
| 3-9 | 3 |
| 8-9 | 3 |
| 2-3 | 2 |
| 4-6 | 2 |
| 0-2 | 1 |
| 0-3 | 1 |
| 0-4 | 1 |
| 0-5 | 1 |
| 0-8 | 1 |
| 1-2 | 1 |
| 1-3 | 1 |
| 1-5 | 1 |
| 2-7 | 1 |
| 2-8 | 1 |
| 4-7 | 1 |
| 5-9 | 1 |
Aperçu de la méthode de correspondance des modèles
Enfin, je voudrais donner un bref aperçu de la méthode de correspondance des modèles. Les données numériques cette fois sont des données 28x28 à 784 dimensions et le nombre de dimensions est élevé, donc il ne peut pas être représenté graphiquement, mais je vais l'expliquer comme s'il était bidimensionnel pour donner une image. Voir le diagramme de dispersion ci-dessous. Les données de chaque classe de nombres peuvent être distinguées par couleur et les données sont dispersées. Ceci est une image d'un ensemble de données sur les enseignants. Prenez cela comme une valeur représentative et faites la moyenne. Les valeurs typiques sont représentées par des points légèrement plus grands sur le graphique.

Par exemple, si le point noir ci-dessous est les données cibles d'identification, la valeur représentative la plus proche est la valeur représentative de la classe «7», de sorte que ces données cibles d'identification sont identifiées comme la classe «7». Il s'agit de la méthode de correspondance des modèles utilisée cette fois.

Recommended Posts