The idea of quicksort

At the beginning

Since the implementation of quicksort explained on the net did not come well, I will upload an article that I summarized myself. The algorithm policy adopts element decomposition and reaggregation, which is often taken up in the explanation of functional languages, and I will try to implement it in Java and see how troublesome it is to implement quicksort in imperative languages.

The idea of quicksort

As an example, consider sorting a set of numbers [6,1,8,5,9]. When doing quicksort, we need a criterion to divide the elements, but here we will use the first element of the set as the criterion.

Disassembled image of the list

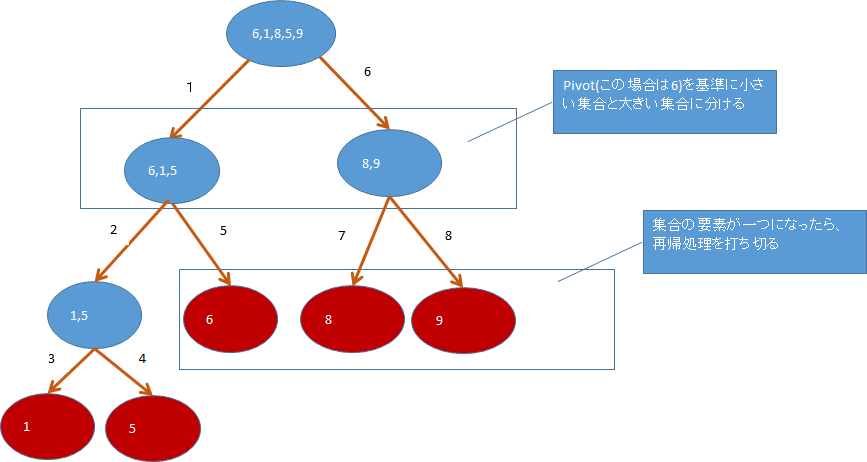
Image of aggregated list after decomposition

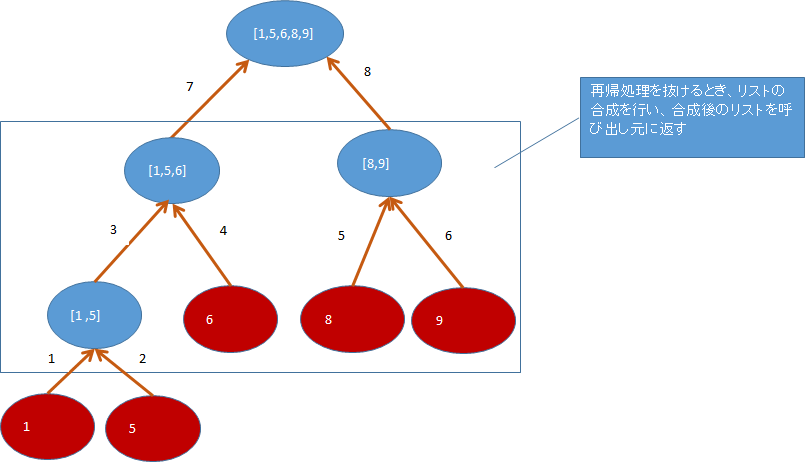
Implementation code

Qsort.java

package test;

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Deque;
import java.util.List;

public class QSort {

	public static void main(String args[]){
		System.out.println(qsort(Arrays.asList(1,5,6,2,11,9,4)));
	}

	public static List<Integer> qsort(List<Integer>list){
		if(list.size()==1){
			//If the array contains one element, exit the recursive process
			return new ArrayList<Integer>(list) ;
		}else{
			//Call the process to split the elements in the list
			Divive div = splitList(list);
			//Generate a list to store the split array
			List<Integer>newList = new ArrayList<Integer>();
			//Perform recursive processing to separate a small set of numbers again
			newList.addAll(qsort(div.leftList));
			//Perform recursive processing to isolate a large set again
			newList.addAll(qsort(div.rightList));
			return newList ;
		}
	}

	//Function to split the list
	public static Divive splitList(List<Integer>list){
		int size =list.size();
		Divive div = new Divive();
		//When the number of elements is two, the size of the elements is compared and the elements are divided.
		if(size==2){
			if(list.get(0)<=list.get(1)){
				div.leftList.add(list.get(0))  ;
				div.rightList.add(list.get(1))  ;
			}else{
				div.leftList.add(list.get(1))  ;
				div.rightList.add(list.get(0))  ;
			}
			return div;
		}

		int pivot = list.get(0);
		List<Integer>smallIntList =new ArrayList<Integer>();
		List<Integer>largeIntList =new ArrayList<Integer>();
		//Divide the list given by the argument into a small set and a large set according to a predetermined criterion.
		for(int i=0;i<size;i++){
			//Generate a set of numbers smaller than the reference
			if(pivot>=list.get(i))smallIntList.add(list.get(i));
			//Generate a set of numbers larger than the reference
			if(pivot<list.get(size - 1- i))largeIntList.add(list.get(size - 1- i));
		}
		
		//If the arguments of the list given in the argument do not match the small set, return the split list combination to the caller.
		if(smallIntList.size()!=list.size()){
			div.leftList.addAll(smallIntList);
			div.rightList.addAll(largeIntList);
		}
		//If the argument of the list given by the argument matches the small set, the reference number is the smallest, so
		//Split the list on the far left of the list and elsewhere
		else{
			Deque<Integer> que  = new ArrayDeque<Integer>(smallIntList);
			div.leftList.add(que.pop()) ;
			div.rightList.addAll(new ArrayList<Integer>(que))  ;
		}
		return div;
	}
	
	//Since Java cannot set a binary value for the return value, it is necessary to define a data structure that represents the set after division.
	static public class Divive{
		List<Integer>leftList =new ArrayList<Integer>();
		List<Integer>rightList =new ArrayList<Integer>();
	}
}