[PYTHON] I tried to simulate ad optimization using the bandit algorithm.
Introduction
The purpose of this entry is to understand the characteristics of each method of the bandit algorithm by performing simulations assuming actual use cases.
The following Qiita post is often referred to in Japanese about the bandit algorithm. http://qiita.com/yuku_t/items/6844aac6008911401b19
The following materials also introduce the details and features of each method and simple simulations. http://www.slideshare.net/greenmidori83/ss-28443892
Since the introduction of the method in the above material is very easy to understand, we will not introduce the method in this entry.
Assumed use case
You are currently running an ad that has been displayed 10,000 times and has a click rate of 1.2% for 60 yen per click. I decided to try different patterns of banners to find more clicked ads. I made 10 new banners. Suppose two of these banners have a better CTR than the current one, three are the same as the current ad, and the other five have a lower CTR than the current one.
--1.3% 2 pieces --1.2% is 3 --1.1% is 3 --Two 1.0%
Why you want to increase your CTR
It has nothing to do with the main subject, but why do you want to increase the click rate, and why does it make sense to experiment when the click rate increases by only 0.1%? Let's think about that. You might think that increasing your CTR doesn't make sense because you pay the same amount of money each time you click. However, from the perspective of the advertiser, placing an ad with a low click rate will reduce sales, so if the click rate is low, it will be difficult to display the ad. At that time, an index called eCPM is often used. eCPM is an index of how much sales can be made by displaying the advertisement 1000 times. Click rate * 1000 * Calculated by the cost per click. Since ads with high EPCM are more likely to be displayed, increasing the click rate will allow many users to be directed to your landing page at the same cost per click. For example, in this case, the click rate is 1.2% and the cost per click is 60 yen, so the eCPM is 720 yen. If the click rate increases by 0.1%, the eCPM will be 780 yen. At that time, even if the cost per click is 56 yen, the eCPM will be 726 yen, which means that if the click rate increases by 0.1%, the unit price for getting the same amount of guidance to the landing page can be reduced by 4 yen. For example, if a product is purchased on that landing page at 1%, the cost of selling one product will be reduced by 400 yen. On a case-by-case basis, increasing CTR in this way is a very important factor in selling things through web advertising.
simulation
The implementation was borrowed from the following
https://github.com/johnmyleswhite/BanditsBook
Let's take a look at Epsilon Greedy, Softmax, UCB
Epsilon Greedy
Epsilon Greedy is a method of choosing an option that you do not think is the best now with a certain probability. First of all, I will try to search at about 10%. Let's try 1000 times.
execfile("core.py")
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
algo1 = EpsilonGreedy(0.1, counts, values)
for t in range(1000):
chosen_arm = algo1.select_arm()
reward = arms[chosen_arm].draw()
algo1.update(chosen_arm, reward)
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of trials | 77 | 109 | 82 | 38 | 38 | 50 | 264 | 205 | 49 | 47 | 41 |
| Evaluation probability | 1.2% | 0.9% | 3.7% | 0% | 0% | 2.0% | 2.3% | 2.0% | 0% | 0% | 0% |
You can't tell at all by trying 1,000 times with 11 options. This result will vary greatly from time to time as it also depends on the generation of random numbers.
What if you try 10,000 times?
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of trials | 1,321 | 824 | 481 | 623 | 1,827 | 562 | 1,026 | 968 | 452 | 1206 | 710 |
| Evaluation probability | 1.2% | 1.2% | 0.6% | 1.2% | 1.3% | 0.7% | 1.2% | 1.1% | 0.9% | 1.2% | 1.3% |
It's not a terrible result, but it's hard to say that it's a good result.
Next, try increasing the degree of search to about 50%. First 1,000 times
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of trials | 239 | 70 | 40 | 72 | 37 | 44 | 137 | 45 | 52 | 211 | 53 |
| Evaluation probability | 1.2% | 1.4% | 0% | 1.4% | 0% | 0% | 1.5% | 0% | 0% | 1.9% | 0% |
Is it a state where Epsilon is being searched evenly compared to when it is 10%? Next 10,000 times
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of trials | 1,035 | 1,915 | 8,120 | 1,046 | 1,026 | 1,104 | 885 | 899 | 1,007 | 1,354 | 1,609 |
| Evaluation probability | 1.2% | 1.3% | 1.3% | 1.1% | 1.1% | 1.0% | 0.9% | 1.1% | 1.1% | 0.7% | 1.2% |
I was able to find the best banner, but it just happened. It can be seen that other banners are being tried evenly compared to when it was 10%. Since there is a large variation from trial to trial, let's evaluate by epcm average repeated multiple times.
eCPM asks for:
def calc_ecpm(algo):
total = sum(algo.counts) - 10000
ecpm = 0.0
for idx, count in enumerate(algo.counts):
if idx == 0:
count -= 10000
if count == 0:
continue
ecpm += 1000 * 60 * algo.values[idx] * float(count)/total
return ecpm
Then, when the parameters are set from 0.1 to 0.9 in 0.1 increments and the bandit of 10,000 trials is executed 1,000 times for each parameter, the ecpm will be like this.
def run_eg(ep, counts, values, arms):
algo = EpsilonGreedy(ep, counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_ecpm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for ep in xrange(1, 10):
print ep * 0.1
for _ in xrange(10000):
data.append((ep*0.1, run_eg(ep*0.1, counts, values, arms)))
return pandas.DataFrame(data, columns=['ep', 'epcm'])
result = run()
result.boxplot(by="ep")

If Epsilon is small, it will vary greatly. However, it seems that the larger the result, the smaller the result. It was also found that it basically exceeds the original ecpm of 720. Even such a simple algorithm seems to give sufficiently useful results.
SoftMax
The parameter of Softmax is tau. The smaller it is, the more you trust the already calculated value. This will try the parameters from 2 ^ -5 to 2 ^ 5 1,000 times each.
def run_sm(tau, counts, values, arms):
algo = Softmax(tau, counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_epcm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for i in xrange(10):
tau = 2**(i - 5)
print tau
for _ in xrange(10000):
data.append((tau, run_sm(tau, counts, values, arms)))
return pandas.DataFrame(data, columns=['tau', 'epcm'])
result = run()
result.boxplot(by="tau")

I got worse results than I normally do! This is because softmax always keeps drawing bad values with a certain probability. When using softmax, it seems necessary to cut off bad options quickly.
UCB
Finally UCB UCB has no parameters so I'll just do it
def run_ucb(counts, values, arms):
algo = UCB1(counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_epcm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for _ in xrange(10000):
data.append(run_ucb(counts, values, arms))
return pandas.DataFrame(data, columns=['epcm'])
result = run()
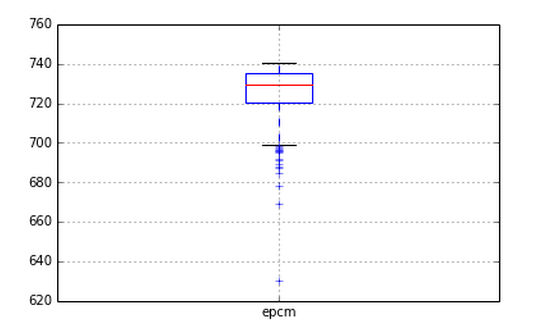
It can be seen that the search can be performed without lowering the epcm. It will be lower than Epsilon Greedy, but this area will probably be a trade-off with search speed.
Comparison and consideration of each method
I want to write it later. I also want to compare it with the A / B test.
Summary
I can't say which method is better in this entry. I think there are a lot of things to think about if you want to explore more use cases, I hope it will lead to some understanding of what the bandit algorithm is.
The bandit algorithm is characterized by being able to search while utilizing the data assets obtained so far. I think one of the benefits is that exploration can reduce the risk of putting a business at risk by lowering important indicators such as eCPM. Therefore, I wanted to verify what kind of utility can be obtained when there are data assets in advance, rather than making the right choice, so I tried this kind of simulation. We hope you find it helpful. And if you have any opinions, please feel free to comment!
Recommended Posts