[PYTHON] Invertiertes Pendel mit modellprädiktiver Steuerung

Ich habe die modellprädiktive Steuerung mit cvxpy versucht, einem der Optimierungsmodule von Python. Als Thema habe ich ein umgekehrtes Pendel gewählt, was keine Übertreibung ist, um Hallo, Welt! Des Steuerungssystems zu sagen.

Modellvorhersagesteuerung und invertiertes Pendel

Grundsätzlich ist der Beispielcode auf der folgenden Site der Hauptcode.

Modellvorhersagesteuerung und Beispielcode

Das umgekehrte Pendel, das diesmal behandelt wird, ist übrigens [umgekehrtes Pendel] von Wikipedia (https://ja.wikipedia.org/wiki/%E5%80%92%E7%AB%8B%E6%8C%AF%E5%AD%90) ) Wird als wagengetriebenes umgekehrtes Pendel angenommen. Die Bewegungsgleichung lautet wie folgt. Jede Variable ist grundsätzlich mit dem Wikipedia-Artikel vereinheitlicht, aber nur F und u sind unterschiedlich.

(M + m)\ddot{x} - ml\ddot{\theta}cos\theta + ml\dot{\theta}^2sin\theta = u \\
l\ddot{\theta} - gsin\theta = \ddot{x}cos\theta

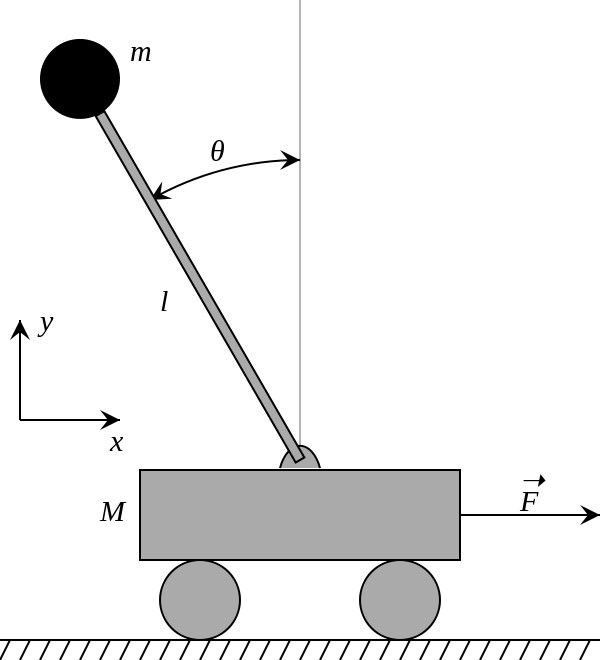
Basierend auf der Annahme, dass θ nahe bei 0 liegt, machen wir eine Näherung und drücken das Modell als lineare Gleichung aus.

\frac{d}{dt}
\begin{pmatrix}
x \\
\dot{x} \\
\theta \\
\dot{\theta}
\end{pmatrix}
=
\begin{pmatrix}
0 & 1 & 0 & 0 \\
0 & 0 & \frac{mg}{M} & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & \frac{(M + m)g}{lM} & 0
\end{pmatrix}
\begin{pmatrix}
x \\
\dot{x} \\
\theta \\
\dot{\theta}
\end{pmatrix}
+
\begin{pmatrix}
0 \\
\frac{1}{M} \\
0 \\
\frac{1}{lM}
\end{pmatrix}
u

A = 
\begin{pmatrix}
0 & 1 & 0 & 0 \\
0 & 0 & \frac{mg}{M} & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & \frac{(M + m)g}{lM} & 0
\end{pmatrix}
Δt
+
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix} \\
B =
\begin{pmatrix}
0 \\
\frac{1}{M} \\
0 \\
\frac{1}{lM}
\end{pmatrix}
Δt

{\bf x}_{t+1} = A{\bf x}_{t} + Bu

Δt ist der Regelzyklus. Wenn Δt 0,1 [s] beträgt, wird der Steuereingang alle 0,1 Sekunden basierend auf dem aktuellen Zustand geändert.

Code

Definieren Sie die lineare Gleichung wie folgt:

mpc.py

import time
from cvxpy import *
import numpy as np
import matplotlib.pyplot as plt

n_state = 4   #Anzahl der Staaten
m_state = 1   #Anzahl der Steuereingänge
T = 100  #Entscheiden Sie, wie viele Schritte vorhergesagt werden sollen

#simulation parameter
delta_t = 0.01

M = 1.0  # [kg]
m = 0.3  # [kg]
g = 9.8  # [m/s^2]
l = 0.6  # [m]

# Model Parameter
A = np.array([
	[0.0, 1.0, 0.0, 0.0],
	[0.0, 0.0, m * g / M, 0.0],
	[0.0, 0.0, 0.0, 1.0],
	[0.0, 0.0, g * (M + m) / (l * M), 0.0]
	])
A = np.eye(n_state) + delta_t * A

B = np.array([
	[0.0],
	[1.0 / M],
	[0.0],
	[1.0 / (l * M)]
	])
B = delta_t * B

#Ausgangszustand des umgekehrten Pendels
#Dieses Mal wollen wir, dass alles gegen 0 konvergiert
x_0 = np.array([
	[-0.02],
	[0.0],
	[0.02],
	[0.0]
	])

x = Variable(n_state, T+1)
u = Variable(m_state, T)

Der folgende Code definiert die Kostenfunktion und optimiert sie. Verwenden Sie cost_arr, um das Gewicht für jeden Status anzupassen. Der Code hier wird fast nur aus Model Predictive Control and Sample Code kopiert.

mpc.py

cost_arr = np.array([
	[1.0, 0.0, 0.0, 0.0],
	[0.0, 1.0, 0.0, 0.0],
	[0.0, 0.0, 0.1, 0.0],
	[0.0, 0.0, 0.0, 0.1]
	])

states = []
for t in range(T):
    #Suchen Sie das Array u so, dass der Wert der Kostenfunktion klein ist
    cost = sum_squares(cost_arr*x[:,t+1]) + sum_squares(0.1*u[:,t])
    #Geben Sie Einschränkungsgleichungen an (lineare Gleichungen und Steuereingabegrenzen).
    constr = [x[:,t+1] == A*x[:,t] + B*u[:,t],
    			norm(u[:,t], 'inf') <= 20.0]
    states.append( Problem(Minimize(cost), constr) )
# sums problem objectives and concatenates constraints.
prob = sum(states)
#Fügen Sie zwei weitere Einschränkungen hinzu
#Letzter Status(Zustand nach T-Schritt)Ist alles 0, das heißt der Idealzustand
#Und da der aktuelle Zustand x0 eine Tatsache ist, wird er zu einer Einschränkung
prob.constraints += [x[:,T] == 0, x[:,0] == x_0]

start = time.time()
result=prob.solve(verbose=True)
elapsed_time = time.time() - start
print("calc time:{0} [sec]".format(elapsed_time))

#Wenn es divergiert, endet es als außer Kontrolle
if result == float("inf"):
    print("Cannot optimize")
    import sys
    sys.exit()

Der obige Code entspricht übrigens einem Steuerelement. Da die Steuerung immer durchgeführt wird, kann das umgekehrte Pendel durch Wiederholen des obigen Vorgangs in einem stehenden Zustand gehalten werden, ohne zu fallen.

Der Code für die iterative Modellvorhersagesteuerung lautet wie folgt.

mpc.py

cnt = 0
#1000-mal kontrollieren
while cnt < 1000:
    states = []
    for t in range(T):
        cost = sum_squares(cost_arr*x[:,t+1]) + sum_squares(0.1*u[:,t])
        constr = [x[:,t+1] == A*x[:,t] + B*u[:,t],
                    norm(u[:,t], 'inf') <= 20.0]
        states.append( Problem(Minimize(cost), constr) )
    # sums problem objectives and concatenates constraints.
    prob = sum(states)
    prob.constraints += [x[:,T] == 0, x[:,0] == x_0]

    start = time.time()
    result=prob.solve(verbose=False)
    elapsed_time = time.time() - start

    if result == float("inf"):
        print("Cannot optimize")
        import sys
        sys.exit()

    #Holen Sie sich das optimale Array von Steuereingängen
    good_u_arr = np.array(u[0,:].value[0,:])[0]
    
    #Geben Sie den Steuereingang ein und erhalten Sie den nächsten Status
    #Ich denke diesmal nicht an Lärm
    x_next = np.dot(A, x_0) + B * good_u_arr[0]
    x_0 = x_next

    cnt += 1

    #Von links nach rechts x(Position des Wagens), \dot{x}(Die Geschwindigkeit des Wagens), rad(Pendelwinkel), \dot{rad}(Winkelgeschwindigkeit des Pendels)
    print(x_next.reshape(-1))

Abhängig vom Ausgangszustand des umgekehrten Pendels ist es oft außer Kontrolle geraten.

Während die modellprädiktive Steuerung eine hohe Steuerungsleistung aufweist, scheint sie das Problem eines großen Rechenaufwands zu haben. Mein PC hat sich auch erheblich aufgewärmt.