[PYTHON] [Einführung] Ich habe versucht, es selbst zu implementieren, während ich erklärte, um die Dichotomie zu verstehen

Die Dichotomie verstehen

Was ist ein gegabelter Baum?

Es ist eine Art nichtlineare Datenstruktur mit einer Baumstruktur.

Tree ADT berücksichtigt nicht die Reihenfolge der Elemente.

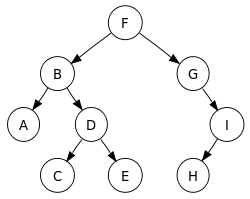
Jeder Knoten hat 0 bis 2 Kinder. Daher können die Wurzel und der linke Teilbaum, der sich links von der Wurzel ausdehnt, und der rechte Teilbaum, der sich nach rechts ausdehnt, allgemein visualisiert werden.

[Erklärung der Dichotomien durch Wikipedia](https://ja.wikipedia.org/wiki/%E6%9C%A8%E6%A7%8B%E9%80%A0_(%E3%83%87%E3%) 83% BC% E3% 82% BF% E6% A7% 8B% E9% 80% A0))

Zweck

• Ich möchte mein Verständnis von Datenstrukturen und Algorithmen vertiefen, indem ich Dichotomie lerne.
• Implementieren Sie eine Dichotomie-Datenstruktur in Python.
• Verstehen Sie, wie Sie mit Dichotomiedatenstrukturen umgehen und nicht nur Dichotomie implementieren.
• Tiefes Graben des grundlegenden Dichotomiebaums, um das Verständnis des Dichotomiebaums zu vertiefen ⇒ Übergeordneter Artikel

Inhalt

Datenstruktur und Knotendefinition

• Knoten hat einen Wert (node.data)
• Haben Sie eine Verbindung zu einem untergeordneten Knoten (node.left = Node (data))
• Die Anzahl der Kinder beträgt entweder 0, 1 oder 2.
• Der oberste Knoten ist der Wurzelknoten (self.root, ins.root)

Implementierung eines gegabelten Baums

Generieren eines Node () - Objekts

Erstellen Sie ein Knotenobjekt und generieren Sie Folgendes im Konstruktor. .Left und .right sind auch None, weil sie zum Zeitpunkt der Generierung nichts mit anderen zu tun haben.

• Knotenwert: self.data = data
• Link zum untergeordneten Knoten des linken Teilbaums: self.left = None
• Link zum untergeordneten Knoten des rechten Teilbaums: self.right = None

Node_class.py

class Node:
    """ Node is user data structure　as binary tree  """
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

Bisektionsbaumgenerierung

1. Erstellen Sie ein Knotenobjekt
2. Suchen Sie den Teil, in dem das Kind kein Element hat, und fügen Sie den Knoten ein.
3. Es gibt mehrere Methoden, die den Knoten in Anbetracht der Reihenfolge der Besuche durchlaufen.

Punkte zum Zeitpunkt der Implementierung

• Erstellen Sie einen Stammknoten im Konstruktor.
• Führen Sie eine Funktion ein, um einen Wert in den Konstruktor einzufügen.
• Die obige Implementierung wird definiert, nachdem sie als Instanzmethode angezeigt wurde
• Wenn Sie die Methode in der Methode von innen beenden möchten, beenden Sie sie mit return

binary_tree.py

class BinaryTree:
    """ user difine data structure BinaryTree """
    def __init__(self, arr):
        self.root = None #Erstellen Sie eine leere Wurzel, die als Grundlage für die zukünftige Verarbeitung dient

        for inserted_node_data in arr: #Verarbeitung zum sequentiellen Einfügen der Werte der in der Liste gespeicherten Knoten
            print('....')
            print('try inserting ', inserted_node_data)
            self.insert(inserted_node_data)

    def insert(self, data):     #Einfügeprozess (Routenerzeugung ⇒ Zweig jedes Knotens erzeugen) ・ ・ ・ Der Wert des linken Zweigs ist kleiner als der des aktuellen Knotens
        if self.root == None:   #Weil der Wurzelknoten ein spezieller Knoten ist, der als Grundlage für die Baumanalyse dient.Fälle, die separat als root generiert werden sollen
            print('Root node is ....')
            self.root = Node(data) # Node()Erstellen Sie eine Instanz und weisen Sie sie zu
            print(self.root.data)

        else:
            level = 1
            flag = True
            next_queue = [self.root] #Erstellen Sie die erste Warteschlange
            while flag:   #Das Flag wird zu False, wenn alle Elemente None sind
                temp_queue, next_queue = next_queue, []
                level += 1

                for node in temp_queue:
                    #Linker Zweig
                    #Fügen Sie den gekühlten Knoten des aktuellen Knotens zur Warteschlange der nächsten Operation hinzu
                    if node.left is not None:
                        next_queue.append(node.left)
                    #Wenn im untergeordneten Knoten Keine gefunden wird, erstellen Sie einen neuen Knoten mit Daten
                    else:
                        node.left = Node(data)
                        print('In level {}, {} is inseted'.format(level, data))
                        """
                        （AA）
Nach dem Hinzufügen von Daten zum Knoten endet diese Einfügung
Hier ist für< while <Da es sich um die Einfügemethode handelt, beenden Sie die Methode mit return auf einmal
                        """
                        return 

                    #Rechter Astbaum
                    #Fügen Sie den gekühlten Knoten des aktuellen Knotens zur Warteschlange der nächsten Operation hinzu
                    if node.right is not None:
                        next_queue.append(node.right)
                    #Wenn im untergeordneten Knoten Keine gefunden wird, erstellen Sie einen neuen Knoten mit Daten
                    else:
                        node.right = Node(data)
                        print('In level {}, {} is inseted'.format(level, data))
                        """
Siehe (AA)
                        """
                        return

                flag = any(next_queue)

    ##########################
    #  Tree traversal
    ##########################
    def preoder_traversal(self, node, res):
        if node != None:
            print('queue', node.data)
            res.append(node.data)

            #Linker Teilbaum in vorheriger Reihenfolge
            self.preoder_traversal(node.left, res)
            #Rechter Teilbaum in vorheriger Reihenfolge
            self.preoder_traversal(node.right, res)

        return res

    def inoder_traversal(self, node, res):
        if node != None:

            #Linker Teilbaum in der richtigen Reihenfolge
            self.inoder_traversal(node.left, res)

            print('queue', node.data)
            res.append(node.data)

            #Richtiger Teilbaum in der richtigen Reihenfolge
            self.inoder_traversal(node.right, res)
        return res

    def postorder_traversal(self, node, res):
        if node != None:
            self.postorder_traversal(node.left, res)
            self.postorder_traversal(node.right, res)
            print('queue', node.data)
            res.append(node.data)
        return res

    def level_order_traversal(self, queue, res= []):

        if queue == [] :
            # it's root
            print('root', self.root.data)
            res.append(self.root.data)
            queue.append(self.root)

        else:
            #Da der Knoten dieser Ebene eine Warteschlange von Argumenten ist, drehen Sie ihn mit for
            temp_list, queue = queue, []
            not_none_cnt = 0

            for item in temp_list:
                if item.left is not None:
                    res.append(item.left.data)
                    print('queue', item.left.data)
                    queue.append(item.left)
                    not_none_cnt += 1

                if item.right is not None:
                    res.append(item.right.data)
                    print('queue', item.right.data)
                    queue.append(item.right)
                    not_none_cnt += 1

            if not_none_cnt == 0:
                return #Gehen Sie zurück zu dem Ort, an dem Sie diese Funktion zuletzt aufgerufen haben

        self.level_order_traversal(queue, res)

        return res

Gabelungsmethode

Implementierte Methoden zum Suchen nach dem Maximalwert, zum Suchen nach Vorhandensein oder Nichtvorhandensein eines Werts, Überprüfen der Größe und Überprüfen der Höhe. Siehe die Kommentare im Code für Punkte.

bt_method.py

#Gabelungsmethode
class BT_method(BinaryTree):
    def __init__(self, arr):
        super().__init__(arr)

    def max_in_binary_tree(self, node, temp_max):
        """Die Implementierung zeigt den Maximalwert in der Eltern-Kind-Beziehung
Dies ist auch dann der Fall, wenn Sie beim Durchqueren LIFO und einen großen Wert hinterlassen.
Gleiches gilt für das Speichern des Maximalwerts beim Durchlaufen der Vorwärtssuche"""
        if node is not None:
            temp_root_val = node.data
            left_val = self.max_in_binary_tree(node.left, temp_max)
            right_val = self.max_in_binary_tree(node.right, temp_max)

            temp_max = max(temp_root_val, left_val, right_val, temp_max)

        return temp_max

    def find_val(self, node, val, flag=False):
        if node != None:
            if node.data == val:
                return True

            else:
                flag_left = self.find_val(node.left, val) #Da das Ergebnis der Wiederholung durch Rückgabe zurückgegeben wird, wird es als Variable empfangen
                flag_right = self.find_val(node.right, val)

                if flag_left or flag_right:
                    return True

        return False


    def size(self, node):
        if node is None: #Beenden Sie die Zählung, wenn der Knoten Keine ist
            return 0 #Wenn 0 zurückgegeben wird, wird es nicht gezählt
        else:
            left_cnt = self.size(node.left)
            right_cnt = self.size(node.right)

            return 1 + left_cnt + right_cnt #I (nicht None) ist 1 und die Zahl im linken und rechten Baum (die virtuelle Suche wird durch eine rekursive Funktion realisiert).


    def hight(self, level=0):
        flag = True
        queue = [self.root]

        while flag:
            level += 1
            temp_list, queue = queue, []
            for node in temp_list:
                if node.left is not None:
                    queue.append(node.left)
                if node.right is not None:
                    queue.append(node.right)


            flag = any(queue)

        return level

Lauf

Ich habe den Code wie folgt ausgeführt.

main.py

ins = BinaryTree(range(1,16))

print('--------------------------')
print('start preoder traversal')
print(ins.preoder_traversal(ins.root, []))

print('--------------------------')
print('start inoder traversal')
print(ins.inoder_traversal(ins.root, []))

print('--------------------------')
print('start postoder traversal')
print(ins.postorder_traversal(ins.root, []))

print('--------------------------')
print('start level order traversal')
print(ins.level_order_traversal([]))

#
print('=====================================')

ins2 = BT_method(range(1,16))
print('--------------------------')
print('find max')
print(ins2.max_in_binary_tree(ins2.root, 0))
print('--------------------------')
print('find value')
print('looking for 7', ins2.find_val(ins2.root, 7))
print('looking for 17', ins2.find_val(ins2.root, 17))


#  search size
print('--------------------------')
print('detect node size')
print(ins2.size(ins2.root))

Ausführungsergebnis

Der Druckteil teilt uns das Verhalten nacheinander mit

....
try inserting  1
Root node is ....
1
....
try inserting  2
In level 2, 2 is inseted
....
try inserting  3
In level 2, 3 is inseted
....
try inserting  4
In level 3, 4 is inseted
....
try inserting  5
In level 3, 5 is inseted
....
try inserting  6
In level 3, 6 is inseted
....
try inserting  7
In level 3, 7 is inseted
....
try inserting  8
In level 4, 8 is inseted
....
try inserting  9
In level 4, 9 is inseted
....
try inserting  10
In level 4, 10 is inseted
....
try inserting  11
In level 4, 11 is inseted
....
try inserting  12
In level 4, 12 is inseted
....
try inserting  13
In level 4, 13 is inseted
....
try inserting  14
In level 4, 14 is inseted
....
try inserting  15
In level 4, 15 is inseted
--------------------------
start preoder traversal
queue 1
queue 2
queue 4
queue 8
queue 9
queue 5
queue 10
queue 11
queue 3
queue 6
queue 12
queue 13
queue 7
queue 14
queue 15
[1, 2, 4, 8, 9, 5, 10, 11, 3, 6, 12, 13, 7, 14, 15]
--------------------------
start inoder traversal
queue 8
queue 4
queue 9
queue 2
queue 10
queue 5
queue 11
queue 1
queue 12
queue 6
queue 13
queue 3
queue 14
queue 7
queue 15
[8, 4, 9, 2, 10, 5, 11, 1, 12, 6, 13, 3, 14, 7, 15]
--------------------------
start postoder traversal
queue 8
queue 9
queue 4
queue 10
queue 11
queue 5
queue 2
queue 12
queue 13
queue 6
queue 14
queue 15
queue 7
queue 3
queue 1
[8, 9, 4, 10, 11, 5, 2, 12, 13, 6, 14, 15, 7, 3, 1]
--------------------------
start level order traversal
root 1
queue 2
queue 3
queue 4
queue 5
queue 6
queue 7
queue 8
queue 9
queue 10
queue 11
queue 12
queue 13
queue 14
queue 15
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
=====================================
....
try inserting  1
Root node is ....
1
....
try inserting  2
In level 2, 2 is inseted
....
try inserting  3
In level 2, 3 is inseted
....
try inserting  4
In level 3, 4 is inseted
....
try inserting  5
In level 3, 5 is inseted
....
try inserting  6
In level 3, 6 is inseted
....
try inserting  7
In level 3, 7 is inseted
....
try inserting  8
In level 4, 8 is inseted
....
try inserting  9
In level 4, 9 is inseted
....
try inserting  10
In level 4, 10 is inseted
....
try inserting  11
In level 4, 11 is inseted
....
try inserting  12
In level 4, 12 is inseted
....
try inserting  13
In level 4, 13 is inseted
....
try inserting  14
In level 4, 14 is inseted
....
try inserting  15
In level 4, 15 is inseted
--------------------------
find max
15
--------------------------
find value
looking for 7 True
looking for 17 False
--------------------------
detect node size
15

Verweise

• Einführung Datenstruktur und Algorithmus (O'Reilly)
• [Erklärung der Gabelung durch Wikipedia](https://ja.wikipedia.org/wiki/%E6%9C%A8%E6%A7%8B%E9%80%A0_(%E3%83%87%E3) % 83% BC% E3% 82% BF% E6% A7% 8B% E9% 80% A0))