Während ich Statistik und maschinelles Lernen studiere, stoße ich auf das Konzept der "Wahrscheinlichkeit". Zunächst erhielt ich einige Kommentare, die ich nicht lesen konnte, aber es war "Yudo". Es ist "plausibel", nicht wahr? Hund: Hund: nicht w Wenn Sie die Wahrscheinlichkeitsfunktion und die Wahrscheinlichkeitsdichtefunktion verstehen, können Sie diese Wahrscheinlichkeit mathematisch behandeln, aber ich möchte versuchen, sie für ein etwas intuitiveres Verständnis grafisch zu erklären.

Den vollständigen Code finden Sie auch auf Github (https://github.com/matsuken92/Qiita_Contents/blob/master/General/Likelihood.ipynb).

Am Beispiel einer Normalverteilung

Die Wahrscheinlichkeitsdichtefunktion der Normalverteilung ist

f(x)={1 \over \sqrt{2\pi\sigma^{2}}} \exp \left(-{1 \over 2}{(x-\mu)^2 \over \sigma^2} \right)

Kann ausgedrückt werden als. In einem Diagramm sieht es so aus.

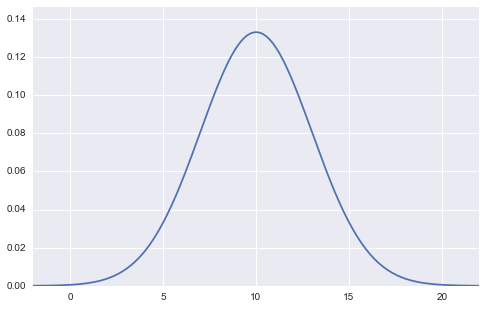
(Abbildung der Normalverteilung mit Mittelwert 10 und Standardabweichung 3)

%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
import seaborn as sns
import numpy.random as rd

m = 10
s = 3

min_x = m-4*s
max_x = m+4*s

x = np.linspace(min_x, max_x, 201)
y = (1/np.sqrt(2*np.pi*s**2))*np.exp(-0.5*(x-m)**2/s**2)

plt.figure(figsize=(8,5))
plt.xlim(min_x, max_x)
plt.ylim(0,max(y)*1.1)
plt.plot(x,y)
plt.show()

In dieser Abbildung sind die Werte der beiden Parameter, Mittelwert $ \ mu $ und Standardabweichung $ \ sigma $, fest (im Fall der obigen Abbildung Mittelwert $ \ mu = 10 $, Standardabweichung $ \ sigma = 3 $). , $ X $ wird als Variable auf der horizontalen Achse genommen. Die vertikale Achse als Ausgabe ist die Wahrscheinlichkeitsdichte $ f (x) $.

Das Grundkonzept der Wahrscheinlichkeitsfunktion besteht darin, die Frage zu beantworten: "Aus welchen Parametern stammten die Daten nach dem Abtasten und Beobachten der Daten ursprünglich?" Ich denke also, dass es einen umgekehrt probabilistischen Bayes'schen Satz gibt. (Tatsächlich ist die Wahrscheinlichkeit ein Bestandteil des Bayes-Theorems.)

(Im Folgenden wird der Begriff "Daten" als "Probe" bezeichnet.)

Hier erhalten wir 10 Stichproben ($ {\ bf x} = (x_1, x_2, \ cdots, x_ {10}) $), von denen wir wissen, dass sie einer Normalverteilung folgen, aber $ \ mu bedeuten Stellen Sie sich eine Situation vor, in der unklar ist, wie hoch die Werte der beiden Parameter $ und der Standardabweichung $ \ sigma $ sind.

plt.figure(figsize=(8,2))
rd.seed(7)
data = rd.normal(10, 3, 10, )
plt.scatter(data, np.zeros_like(data), c="r", s=50)

Betrachten wir zunächst "gleichzeitige Verteilung, bei der 10 Proben diesen Wert haben". Wir gehen auch davon aus, dass diese 10 Proben iid sind (unabhängige identische Verteilung: Proben, die unabhängig von derselben Verteilung entnommen wurden). Da es unabhängig ist, kann es als Produkt jeder Wahrscheinlichkeitsdichte ausgedrückt werden.

P(x_1, x_2,\cdots,x_{10}) = P(x_1)P(x_2)\cdots P(x_{10})

Es wird sein. Da $ P (x_i) $ hier normalerweise verteilt war,

P(x_1, x_2,\cdots,x_{10}) = f(x_1)f(x_2)\cdots f(x_{10})

Es ist auch gut. Wenn Sie dies weiter ausbauen und schreiben

P(x_1, x_2,\cdots,x_{10}) = \prod_{i=1}^{10} {1 \over \sqrt{2\pi\sigma^{2}}} \exp \left(-{1 \over 2}{(x_i-\mu)^2 \over \sigma^2} \right)

ist. Das Exemplar $ x_i $ befindet sich jetzt in $ \ exp (\ cdot) $.

Sie haben jetzt eine simultane Wahrscheinlichkeitsdichtefunktion für 10 Stichproben. Aber warte eine Minute. Nachdem wir die Stichprobe als realisierten Wert haben, ist sie kein unsicherer Wahrscheinlichkeitswert mehr. Es ist ein fester Wert. Vielmehr kannte ich die beiden Parameter $ \ mu $ und Standardabweichung $ \ sigma $ nicht. Stellen Sie sich also $ x_i $ als Konstante vor und ändern Sie Ihre Meinung, um zu sagen, dass $ \ mu $ und $ \ sigma $ Variablen sind.

Die Form der Funktion ist genau dieselbe, und die erneute Deklaration der Variablen als $ \ mu $ und $ \ sigma $ wird als Wahrscheinlichkeit definiert.

L(\mu, \sigma) = \prod_{i=1}^{10} {1 \over \sqrt{2\pi\sigma^{2}}} \exp \left(-{1 \over 2}{(x_i-\mu)^2 \over \sigma^2} \right)

Wird besorgt. Die Form der rechten Seite ändert sich überhaupt nicht. Aber die Bedeutung hat sich geändert.

Ich werde dies als Grafik verstehen.

Schreiben und verstehen Sie Grafiken

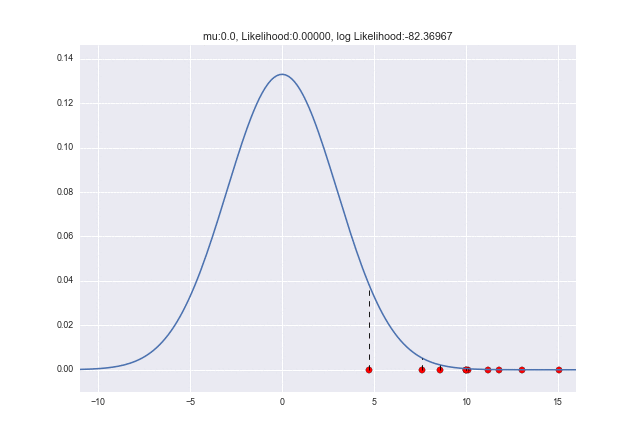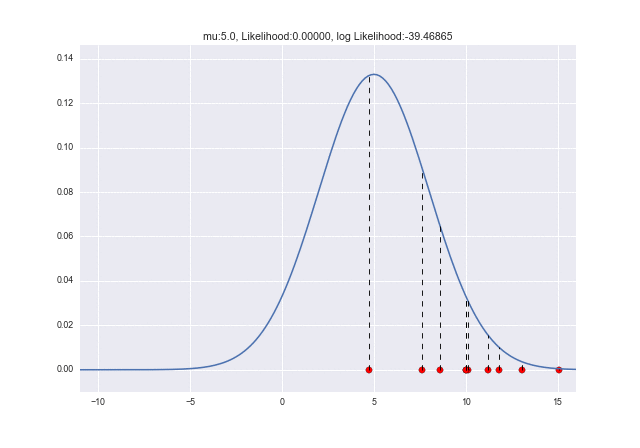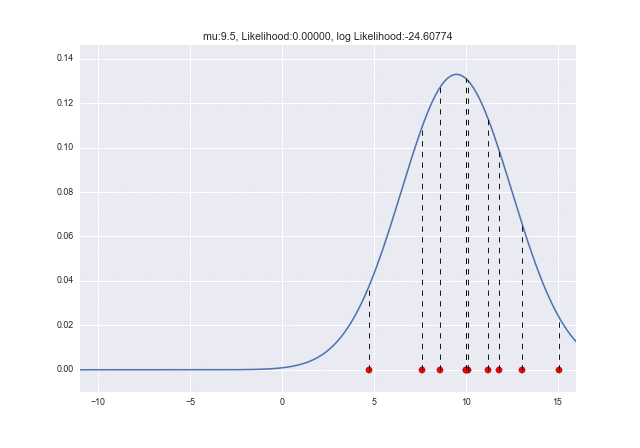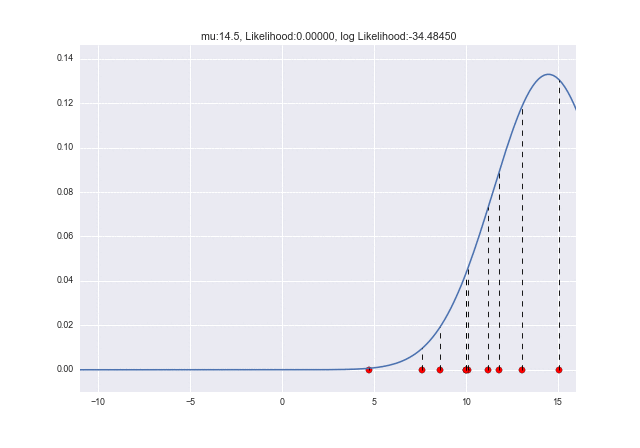
Da $ \ mu $ und $ \ sigma $ unbekannt sind, wenn Sie denken, dass $ \ mu = 0 $ und $ \ sigma = 1 $ und ein Diagramm zeichnen,

Es wird sein. Es fühlt sich an, als wäre es komplett entfernt. Zu diesem Zeitpunkt ist die Wahrscheinlichkeit ebenfalls gering.

(Da die Wahrscheinlichkeit durch Multiplizieren der Wahrscheinlichkeit (Dichte) mit der Anzahl der Abtastwerte berechnet wird, wird die Zahl zwischen 0 und 1 um ein Vielfaches multipliziert, und die Multiplikation ist eine ziemlich kleine Zahl, fast 0. Da es leicht hinzuzufügen ist, wird es häufig als logarithmische Wahrscheinlichkeit verwendet. In diesem Fall kann der numerische Wert im Titel des obigen Diagramms leicht verstanden werden.)

m = 0
s = 1


min_x = m-4*s
max_x = m+4*s

def norm_dens(val):
    return (1/np.sqrt(2*np.pi*s**2))*np.exp(-0.5*(val-m)**2/s**2)
                                      
x = np.linspace(min_x, max_x, 201)
y = norm_dens(x)

L = np.prod([norm_dens(x_i) for x_i in data])
l = np.log(L)

plt.figure(figsize=(8,5))
plt.xlim(min_x, 16)
plt.ylim(-0.01,max(y)*1.1)

#Zeichnen der Dichtefunktion der Normalverteilung
plt.plot(x,y)

#Datenpunkte zeichnen
plt.scatter(data, np.zeros_like(data), c="r", s=50)
for d in data:
    plt.plot([d, d], [0, norm_dens(d)], "k--", lw=1)
    
plt.title("Likelihood:{0:.5f}, log Likelihood:{1:.5f}".format(L, l))

plt.show()

Da sich die Stichprobe dort befindet, wo die Wahrscheinlichkeitsdichtefunktion fast 0 ist, hat $ L (\ mu, \ sigma) $ auch eine relativ geringe Wahrscheinlichkeit (logarithmische Wahrscheinlichkeit: etwa -568).

Versuchen wir diesmal $ \ mu = 5 $ und $ \ sigma = 4 $. (Der Code wird gegenüber dem vorherigen nur bei $ \ mu = 5 $ und $ \ sigma = 4 $ geändert.)

Die gepunktete Linie zeigt die Wahrscheinlichkeit, die jeder Probe entspricht. Es fühlt sich an, als würde es etwas wärmer als zuvor. Diesmal hat sich die logarithmische Wahrscheinlichkeit erheblich auf etwa -20 erhöht.

Animiert und intuitiver

Verwenden wir eine Animation, um zu sehen, wie sich die Wahrscheinlichkeit ändert, wenn sich $ \ mu $ ändert. Sie können sehen, dass die Protokollwahrscheinlichkeit bei $ \ mu = 10 $ maximal ist: grinsen:

from matplotlib import animation as ani

num_frame = 30

min_x = -11
max_x = 21

x = np.linspace(min_x, max_x, 201)

    
def norm_dens(val, m, s):
    return (1/np.sqrt(2*np.pi*s**2))*np.exp(-0.5*(val-m)**2/s**2)
    
def animate(nframe):
    global num_frame
    plt.clf()
    
    m = nframe/float(num_frame) * 15
    s = 3
    y = norm_dens(x, m, s)
    
    L = np.prod([norm_dens(x_i, m, s) for x_i in data])
    l = np.log(L)

    plt.xlim(min_x, 16)
    plt.ylim(-0.01,max(y)*1.1)

    #Zeichnen der Dichtefunktion der Normalverteilung
    plt.plot(x,y)

    #Datenpunkte zeichnen
    plt.scatter(data, np.zeros_like(data), c="r", s=50)
    for d in data:
        plt.plot([d, d], [0, norm_dens(d, m, s)], "k--", lw=1)

    plt.title("mu:{0}, Likelihood:{1:.5f}, log Likelihood:{2:.5f}".format(m, L, l))

    #plt.show()
    
fig = plt.figure(figsize=(10,7))
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('likelihood.gif', writer='imagemagick', fps=1, dpi=64)

Wenn sich $ \ sigma $ ändert, können Sie sehen, dass die logarithmische Wahrscheinlichkeit maximal ist, wenn $ \ sigma = 2.7 $. Als die Daten ursprünglich generiert wurden, war es $ \ sigma = 3 $, daher liegt ein kleiner Fehler vor, aber die Werte liegen nahe beieinander: kissing_closed_eyes:

num_frame = 30

min_x = -11
max_x = 21

x = np.linspace(min_x, max_x, 201)
    
def norm_dens(val, m, s):
    return (1/np.sqrt(2*np.pi*s**2))*np.exp(-0.5*(val-m)**2/s**2)
    
def animate(nframe):
    global num_frame
    plt.clf()
    
    m = 10
    s = nframe/float(num_frame) * 5
    y = norm_dens(x, m, s)
    
    L = np.prod([norm_dens(x_i, m, s) for x_i in data])
    l = np.log(L)

    plt.xlim(min_x, 16)
    plt.ylim(-0.01,.6)

    #Zeichnen der Dichtefunktion der Normalverteilung
    plt.plot(x,y)

    #Datenpunkte zeichnen
    plt.scatter(data, np.zeros_like(data), c="r", s=50)
    for d in data:
        plt.plot([d, d], [0, norm_dens(d, m, s)], "k--", lw=1)

    plt.title("sd:{0:.3f}, Likelihood:{1:.5f}, log Likelihood:{2:.5f}".format(s, L, l))

    #plt.show()
    
fig = plt.figure(figsize=(10,7))
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('likelihood_s.gif', writer='imagemagick', fps=1, dpi=64)

Höchstwahrscheinlich Schätzung

Es ist ein Diagramm der Änderung der logarithmischen Wahrscheinlichkeit, wenn $ \ mu $ geändert wird. Sie können sehen, dass der Wert von $ \ mu $ bei 10 liegt, wenn die Wahrscheinlichkeit durch $ \ mu $ differenziert und auf 0 gesetzt wird. Dies ist die wahrscheinlichste Schätzung. (Angenommen, s ist vorerst festgelegt)

#Ändern Sie m

list_L = []
s = 3

mm = np.linspace(0, 20,300)
for m in mm:
    list_L.append(np.prod([norm_dens(x_i, m, s) for x_i in data]))
    

plt.figure(figsize=(8,5))
plt.xlim(min(mm), max(mm))
plt.plot(xx, (list_L))
plt.title("Likelihood curve")
plt.xlabel("mu")

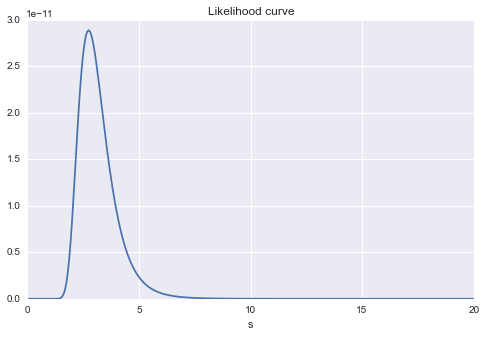
Es ist auch ein Diagramm der Änderung der Wahrscheinlichkeit für Änderungen in $ s $. Sie können immer noch sehen, dass es wahrscheinlich einen Maximalwert um $ s = 3 $ gibt.

#Änderungen

list_L = []
m = 10

ss = np.linspace(0, 20,300)
for s in ss:
    list_L.append(np.prod([norm_dens(x_i, m, s) for x_i in data]))
    
plt.figure(figsize=(8,5))
plt.xlim(min(ss), max(ss))
plt.plot(ss, (list_L))
plt.title("Likelihood curve")
plt.xlabel("s")

Wenn Sie schließlich $ \ mu $ und $ \ sigma $ gleichzeitig betrachten, ist $ \ mu $ etwas mehr als 10 und $ \ sigma $ etwas weniger. Sie können sehen, dass der Wert von \ sigma $ wahrscheinlich ist: zufrieden:

#Kontur

plt.figure(figsize=(8,5))
mu = np.linspace(5, 15, 200)
s = np.linspace(0, 5, 200)
MU, S = np.meshgrid(mu, s)

Z = np.array([(np.prod([norm_dens(x_i, a, b) for x_i in data])) for a, b in zip(MU.flatten(), S.flatten())])
plt.contour(MU, S, Z.reshape(MU.shape), cmap=cm.Blues)
plt.xlabel("mu")
plt.ylabel("s")

[PYTHON] [Statistik] Was ist Wahrscheinlichkeit? Lassen Sie uns grafisch erklären.

Am Beispiel einer Normalverteilung

Schreiben und verstehen Sie Grafiken

Animiert und intuitiver

Höchstwahrscheinlich Schätzung