Die Bildverarbeitung ist schwierig. Wenn Sie sich die wunderschönen Filter von Instagram, die Photo Sphere von Google und diese Dienste ansehen, sehen die Bilder interessant aus! Ein Bildverarbeitungsbuch, das vor Aufregung geöffnet wurde. Wir hatten keine andere Wahl, als die dort aufgeführten mathematischen Formeln zu versteinern, aber was bleibt der Stimme übrig, die in unseren Ohren flüsterte: "OpenCV wird die schwierigen Dinge tun, richtig?" Ich hätte es tun können.

Ich hoffe, dass dieser Artikel denjenigen den Weg zeigt (in Bezug auf Gegenstände, Goldnadeln), die jene Tage überwinden wollen, in denen sie die grundlegende Theorie versteinern und verstehen mussten, während sie OpenCV verwendeten. Überlegen. Der behandelte Bereich ist "Praktische Computer Vision" (https://www.oreilly.co.jp/books/9784873116075/), die die Grundlage aller Verarbeitung bildet. Äquivalent). Da dieser Artikel selbst geschrieben wurde, während ich Anfänger bin, würde ich es begrüßen, wenn fortgeschrittene Abenteurer der Bildverarbeitung auf Fehler hinweisen könnten.

Was sind die Merkmalspunkte des Bildes?

Warum können Menschen Puzzles zusammensetzen? Wenn wir darüber nachdenken, können wir uns vorstellen, dass wir die Eigenschaften jedes Puzzleteils erfassen, ähnliche und kontinuierliche Eigenschaften finden und sie miteinander verbinden. Ebenso können Sie mehrere Fotos zu einem Panoramafoto kombinieren, da Sie gemeinsame Funktionen zwischen den Fotos finden und verbinden.

CS231M Mobile Computer Vision Class,Lecture5, Stitching + Blending, p4~

Wenn Sie diese "Funktionspunkte" immer einfacher betrachten, können Sie sie schließlich in den folgenden drei zusammenfassen.

Kante: Es gibt eine Grenze, an der der Unterschied erkannt werden kann
Ecke: Der Punkt, an dem die Kanten konzentriert sind
flach: Weder Kante noch Ecke, der Punkt, an dem kein Merkmal erkannt werden kann

In Anbetracht der oben beschriebenen Zusammensetzung von Panoramafotos ist es erforderlich, die folgenden Regeln zu befolgen, um diesen "Merkmalspunkt" zu finden.

Reproduzierbarkeit: Ein Feature-Punkt wird immer als Feature-Punkt erkannt
Unterscheidbarkeit: Ein Merkmalspunkt kann als deutlich anders als andere Merkmalspunkte identifiziert werden

In Bezug auf die Reproduzierbarkeit beispielsweise wird der Prozess des Verbindens der Merkmalspunkte unterbrochen, wenn sich die Merkmalspunkte, die erkannt werden, wenn sich der Winkel, in dem das Bild aufgenommen wird, erkennt, drastisch ändert.

Daher ist es besser, robuste Merkmalspunkte ** zu erkennen, die sich nicht mit dem Winkel oder der Vergrößerung des Bildes ändern.

In Bezug auf die Unterscheidungskraft ist es schwierig zu wissen, welche Punkte übereinstimmen, wenn die erkannten Merkmalspunkte nicht eindeutig identifiziert werden können.

Daher ist es wichtig, über eine Darstellungsmethode zu verfügen, mit der jeder Merkmalspunkt eindeutig identifiziert werden kann.

Dies ist genau das, was für die Feature-Erkennung und Feature-Beschreibung erforderlich ist. Mit anderen Worten, das Erkennen "eines robusten Merkmalspunkts, der sich nicht mit dem Winkel oder der Vergrößerung des Bildes ändert" (Merkmalerkennung) und das Ausdrücken mit einer "eindeutig identifizierbaren Ausdrucksmethode" (Merkmalbeschreibung) ist das Bild. Es ist das Ziel, Merkmalspunkte zu erkennen.

Betrachten wir nun die Erkennung von Feature-Punkten und die Ausdrucksmethode von Feature-Punkten in der angegebenen Reihenfolge.

Funktionserkennung

Das Verfahren zum Erkennen von Merkmalspunkten besteht im Allgemeinen darin, "die Kante zu erkennen" und dann "die Ecke zu erkennen", wo die Kanten konzentriert sind.

Kantenerkennung

Insbesondere ist die Kante der "Punkt, an dem sich die Helligkeit erheblich ändert". Betrachten Sie als einfaches Beispiel ein Bild einer schwarzen Kachel mit einem weißen Kreis. Wenn Sie die Helligkeit auf der roten Linie zeichnen, die von der Seite wie unten gezeigt entlang der Koordinatenachsen gezeichnet wird, sollten Sie ein Diagramm erhalten, in dem die Helligkeit in den weißen Kreis in der Mitte springt.

Hier möchten wir die Kante erkennen, dh den Punkt im Diagramm, der sich erheblich von dunkel-> hell, hell-> dunkel ändert. Um den Änderungsgrad an einem bestimmten Punkt zu ermitteln, berechnen wir die Änderungsrate aus den Werten der Punkte vor und nach diesem Punkt.

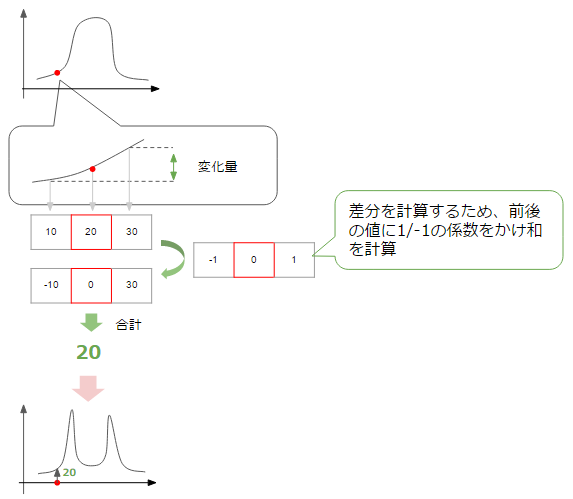
Dann können Sie, wie in der obigen Abbildung gezeigt, ein Diagramm erhalten, in dem die Änderungsrate an dem Punkt zunimmt, an dem die Änderung groß ist, dh an dem Teil, der der Kante entspricht (der Änderungsbetrag hat + -, aber hier ist der Absolutwert aufgetragen. Bitte denken Sie). Im Moment betrachten wir das Ausmaß der Änderung in der horizontalen Richtung der Figur, aber das gleiche kann in der vertikalen Richtung berücksichtigt werden.

Letztendlich scheint es, dass eine Kante erkannt werden kann, indem das Ausmaß der Änderung sowohl in horizontaler als auch in vertikaler Richtung (normalerweise die Summe der Quadratwurzeln) summiert und Punkte gesammelt werden, deren Wert größer als ein bestimmter Schwellenwert (Schwellenwert) ist.

Dies ist die Grundidee der Kantenerkennung, und obwohl die Kantenerkennung allein damit möglich ist, gibt es einige Techniken für eine genauere Erkennung. Schauen wir uns das an.

Glätten

Dies ist eine Methode, die bei der Berechnung des Änderungsbetrags auch den peripheren Teil berücksichtigt. Grob gesagt ist es wie ein Durchschnitt. Durch Mittelung kann die Wertänderung geglättet werden (Glättung), und als Ergebnis können glatt verbundene Kanten erkannt werden.

Die folgende Abbildung zeigt, wie der Änderungsbetrag in horizontaler Richtung unter Berücksichtigung des Änderungsbetrags an benachbarten Punkten berechnet wird. Die Glättung wird durch Summieren von insgesamt drei Änderungen erreicht.

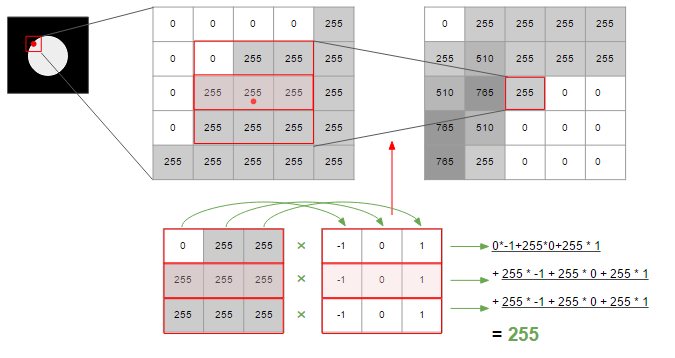
In der obigen Abbildung wird zur Berechnung des Änderungsbetrags eine Matrix berechnet, die den Wert -1/0/1 von 3 * 3 enthält. Die Matrix und die Verarbeitung zur Berechnung solcher Änderungen werden als ** Filter ** bezeichnet.

Es gibt verschiedene Arten dieses Filters, und der in der obigen Abbildung verwendete ist der Prewitt-Filter. Der Sobel-Filter konzentriert sich mehr auf das, was an die Mitte angrenzt als Prewitt, und Gauß kann eine Funktion der Normalverteilung verwenden, wobei die Mitte als Spitze dient und der Koeffizient sanft zur Kante hin multipliziert wird. Die Canny-Methode, die häufig zum Erkennen von Kanten verwendet wird, verwendet diesen Gaußschen Filter.

Beachten Sie, dass die Bildränder interpoliert werden müssen, da keine benachbarten Punkte vorhanden sind. Für diese Interpolationsmethode gibt es die folgenden Methoden.

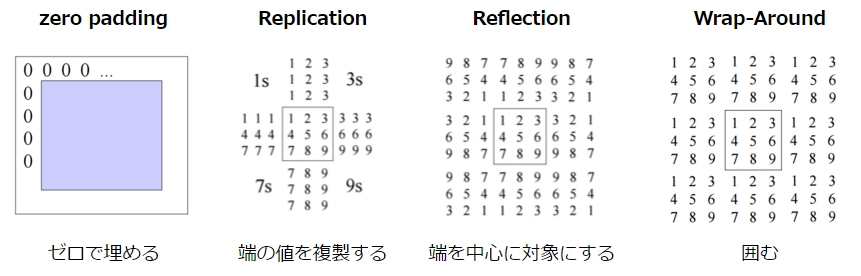CSE/EE486 Computer Vision I, Lecture3, p26~

Das ist alles für die Kantenerkennung. Ich werde den Inhalt bisher zusammenfassen.

Um die Kante zu erkennen, verwenden Sie das Ausmaß der Helligkeitsänderung im Bild als Hinweis.
Das Ausmaß der Änderung kann in zwei Richtungen erfolgen, in horizontaler und in vertikaler Richtung. Die Summe der Quadratwurzeln dieses Wertes wird als Änderungsbetrag verwendet, und dies wird als Größe bezeichnet.
Die Kante kann durch Bestimmen der Kante erkannt werden, wenn die Größe einen bestimmten Schwellenwert überschreitet.
Bei der Berechnung des Änderungsbetrags wird im Allgemeinen eine Glättung durchgeführt. Dies dient zur Verbesserung der Erkennungsgenauigkeit durch Hinzufügen des Änderungsbetrags in der Umgebung.
Filter definieren den Umfang dieser "Peripherie" und die Gewichtung dafür, und es gibt verschiedene Arten.

Eckenerkennung

Als nächstes folgt die Erkennung der Ecke. Hier erklären wir den Harris Corner Detector, der häufig zur Erkennung von Ecken verwendet wird. Dies ist eine Methode, die die Eigenschaften der Matrix sehr gut nutzt und intuitiv ein Bild liefert, das der Hauptkomponentenanalyse nahe kommt.

Ich werde die ausführliche Erläuterung der Hauptkomponentenanalyse anderen Artikeln überlassen, aber die folgenden zwei Punkte sind wichtig.

Finden Sie einen Indikator, der die Richtung erklären kann, in die sich die Daten verbreiten. Dies entspricht dem Eigenvektor der Matrix.
Der durch die Berechnung erhaltene eindeutige Wert repräsentiert die Aussagekraft des Index.

Wenn man dies auf Harris anwendet, sind die "Daten" natürlich eine Zusammenfassung des Ausmaßes der Änderung in jeder der horizontalen und vertikalen Richtungen an einem bestimmten Punkt. Aus der obigen Erläuterung der Hauptkomponentenanalyse kann dann wie folgt geschlossen werden.

Der Eigenvektor repräsentiert die "Richtung, in die sich das Ausmaß der Änderung ausbreitet", dh die Richtung der Kante.
Wenn der Eigenwert groß ist, bedeutet dies, dass "die Fähigkeit, das Ausmaß der Änderung zu erklären, hoch ist", dh die Stärke der Kante.

Dies ermöglicht es, zuerst Kanten zu erkennen, und wenn es "mehrere Eigenvektoren mit großen Eigenwerten" gibt, dann gibt es mehrere Kanten, dh Ecken. Unter der Annahme, dass die eindeutigen Werte $ \ lambda1 $ bzw. $ \ lambda2 $ sind, können sie entsprechend der Größe der Werte wie folgt klassifiziert werden.

CSE/EE486 Computer Vision I, Lecture 06, Corner Detection, p19

Ich werde auch die Formel erklären. Zuerst bewegten sich ein Punkt $ I (x, y) $ auf dem Bild $ I $ und ein Punkt $ I (x + u, y + v) um $ u $ in Richtung $ x $ und $ v $ in Richtung $ y $. Wenn der Änderungsbetrag zwischen) $ $ E (u, v) $ beträgt, kann dies in der Formel wie folgt ausgedrückt werden.

E(u, v) = \sum_{x, y} w(x, y) [I(x+u, y+v) - I(x, y)]^2

$ w (x, y) $ ist eine Fensterfunktion, die zu einem Filter (Gauß) wird. Das Bild ist, dass der Änderungsbetrag $ [I (x + u, y + v) - I (x, y)] ^ 2 $ ist, und dies wird mit $ w (x, y) $ geglättet, um den Änderungsbetrag zu berechnen. ist. Die Annäherung dieser Formel mithilfe der Taylor-Erweiterung lautet wie folgt (die Erweiterungsformel wird weggelassen. Wenn Sie interessiert sind, lesen Sie bitte das oben verlinkte Vorlesungsmaterial).

E(u, v) \simeq [u, v] M \begin{bmatrix} u \\ v \end{bmatrix}

Wo $ M $ ist:

M = \sum_{x, y} w(x, y) \begin{bmatrix} I_X^2 & I_x I_y \\ I_x I_y & I_y ^2 \end{bmatrix}

$ I_x $ und $ I_y $ sind die Unterschiede auf der x-Achse bzw. der y-Achse, und wenn $ [I_x, I_y] $ quadriert wird, wird der obige Matrixteil erhalten. Was Sie tun, ist dasselbe wie $ [I (x + u, y + v) - I (x, y)] ^ 2 $ in der obigen Formel. Und dies ist die "Matrix, die das Ausmaß der Änderung beschreibt", und durch Zerlegen dieser in singuläre Werte ist es möglich, die Kante und Ecke wie zu Beginn beschrieben zu beurteilen.

Es ist jedoch ziemlich mühsam, den Eigenwert zu berechnen. Versuchen Sie daher, ihn nicht dort zu berechnen, wo er nicht benötigt wird. Zu diesem Zweck werden die folgenden Indikatoren verwendet.

R = det M -k(trace M)^2

det M = \lambda1 \lambda2

trace M = \lambda1 + \lambda2

$ k $ ist eine Konstante, ungefähr 0,04 ~ 0,06. Es kann gemäß dem Wert von R wie folgt klassifiziert werden.

Große R: Ecke
Kleines R: flach
R < 0: edge

Die Figur ist wie folgt.

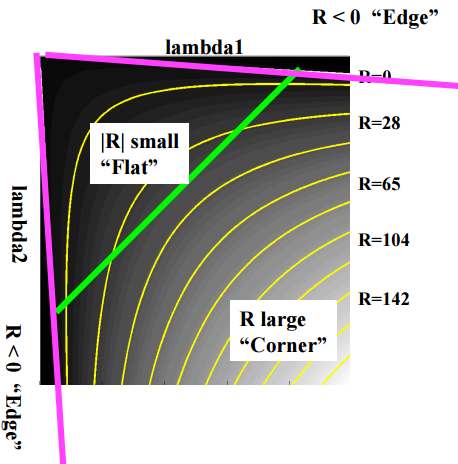CSE/EE486 Computer Vision I, Lecture 06, Corner Detection, p22

Jetzt können Sie die Ecke schnell erkennen. Hier ist eine Zusammenfassung der Eckenerkennung.

Ecke kann als Ort definiert werden, an dem sich mehrere Kanten versammeln
Die Richtung der Kante kann aus dem Eigenvektor der Matrix ermittelt werden, der den Änderungsbetrag zusammenfasst, und die Größe des Änderungsbetrags (Kantenähnlichkeit) kann aus der Größe des Eigenwerts ermittelt werden.
Kante, Ecke und Ebene können basierend auf den Werten der beiden eindeutigen Werte bestimmt werden.
Da die Berechnung des Eigenwerts schwierig ist, verwenden Sie die Beurteilungsformel, um die Berechnung zu vereinfachen.

Da Harris den Eigenvektor betrachtet, der die Richtung der Kante ist, ist er robust gegen die Neigung des Bildes. Es ist jedoch nicht robust, wenn es um Skalierung geht. Dies liegt daran, dass die Ecken beim Erweitern lockerer werden, was die Unterscheidung der Kanten erschwert.

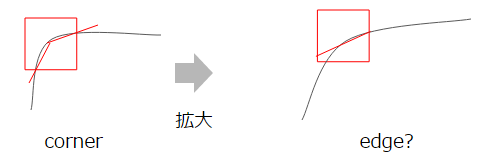
FAST ist eine Methode, um dies zu überwinden. Ich werde die Details weglassen, aber es ist eine Methode, eine Reihe von n Punkten zu erkennen, die dunkler oder heller als der Mittelpunkt sind. Dies ist buchstäblich eine SCHNELLE Methode und robust gegen Rotation und Expansion.

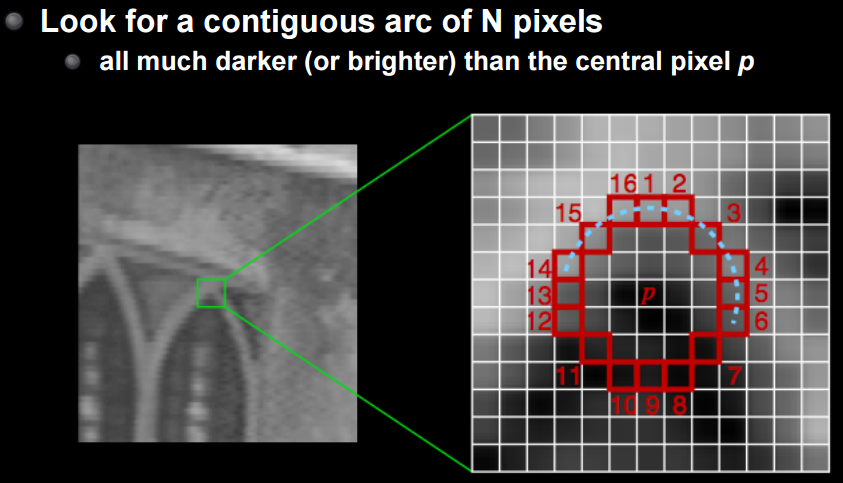CS231M Mobile Computer Vision Class,Lecture5, Stitching + Blending, p24

Funktionsbeschreibung

Die Feature-Punkte können jetzt erkannt werden. Beim nächsten Mal möchte ich in der Lage sein, Bilder abzugleichen, indem ich mithilfe der Feature-Punkte einen eindeutigen Feature-Ausdruck und eine Feature-Beschreibung erstelle.

Wie ich ein wenig erwähnt habe, sind die folgenden drei Eigenschaften für diese Funktionsbeschreibung wünschenswert.

Übersetzung: Robust für Bildfolien
Drehung: Robust gegen Bilddrehung
Skalierung: Robust für Bildvergrößerung / -verkleinerung

Die Übersetzung ist relativ einfach zu handhaben, da sie lediglich ihre Position ändert und die Rotation recht gut ist, wie in Harris im vorherigen Abschnitt erwähnt. Es ist jedoch schwierig, die Skalierung zu unterstützen. Wie Sie der folgenden Abbildung entnehmen können, ändern sich die Informationen im Bild je nach Vergrößerung erheblich.

CSE/EE486 Computer Vision I, Lecture 31, Object Recognition : SIFT Keys, p31

Wenn Sie es erweitern, ist es offensichtlich, dass die Informationen verloren gehen, wenn Sie den Übereinstimmungsbereich nicht entsprechend erweitern. Dies liegt daran, dass sich der Bereich ändert, der in denselben Bereich passt.

Mit anderen Worten ist es notwendig, die Skala zu berücksichtigen, um die obigen drei Eigenschaften zu erfüllen. In Harris war es nur "Richtung" und "Stärke" aus dem Eigenvektor und dem Eigenwert, aber hier soll "Skala" hinzugefügt werden, dh welcher Vergrößerungswert wird erhalten. Das Bild sieht wie folgt aus.

Die SIFT-Methode ermöglicht die Erkennung und Beschreibung von Merkmalspunkten, die diese Skala berücksichtigen.

SIFT (Scale Invariant Feature Transform)

Das Herzstück von SIFT ist die Extraktion von Merkmalspunkten für jede Skala. Die hierfür verwendete Methode ist LoG / DoG. Log ist eine Abkürzung für Laplace von Gauß, und der Punkt mit der größten Änderung des durch das Gauß-Filter geglätteten Bildes wird durch doppelte Differenzierung (= Laplace) erhalten. Da Gauß wie in Glättung beschrieben ist, werde ich kurz erklären, warum der Punkt mit dem maximalen Änderungsbetrag durch das Differential zweiter Ordnung (= Laplace) erhalten wird.

Stellen Sie sich Differenzierung so vor, als würden Sie einfach das Ausmaß der Veränderung an einem bestimmten Punkt finden. Dann können Sie Folgendes sehen.

Differenzierung erster Ordnung: Repräsentiert den Änderungsbetrag in Bezug auf die ursprüngliche Funktion = Der Scheitelpunkt repräsentiert den Punkt, an dem der Änderungsbetrag maximal (minimal) ist.
Differenzierung zweiter Ordnung: Eine Änderung der Änderungsrichtung erfolgt nahe dem Scheitelpunkt der Differenzierung erster Ordnung, die die Änderung des Änderungsbetrags darstellt. Der Scheitelpunkt der Differenzierung erster Ordnung ist gleich dem Nulldurchgangspunkt.

Mit anderen Worten, der Punkt, an dem $ I (x) '' = 0 $ ist, wird als der Punkt mit der größten Änderungsmenge und der Merkmalspunkt angehoben. Das Filter, das der Anwendung dieser quadratischen Differenzierung entspricht, wird als "Rapras-Filter" bezeichnet. Je näher der Wert an 0 liegt, desto höher ist die Wahrscheinlichkeit von Merkmalspunkten.

Es ist jedoch nicht möglich, zwischen 0 (= keine Änderung) Punkten und denen am Scheitelpunkt im Stadium der Differenzierung erster Ordnung nur durch die Differenzierung zweiter Ordnung zu unterscheiden, so dass gleichzeitig geprüft werden muss, ob der Wert der Differenzierung erster Ordnung ausreichend groß ist. Wie Sie daran sehen können, ist es sehr anfällig für Lärm.

Wenn Sie dann zu LoG zurückkehren, wie der Name schon sagt, ist dies eine Methode zum Glätten mit einem Gaußschen Filter und zum Finden des Punkts mit der maximalen Änderungsmenge = Merkmalspunkt mit einem Laplace-Filter. Und da LoG einen Gaußschen Filter verwendet, können Sie dessen $ \ sigma $ (Verteilung) anpassen. Je größer das $ \ sigma $ ist, desto stärker ist die Glättung, sodass nur erkannt werden kann, wo Punkte mit großen Änderungen gesammelt werden. Dies ist umgekehrt, und wie Sie vielleicht bemerkt haben, spielt es die gleiche Rolle wie nur die Manipulation der Vergrößerung.

CSE/EE486 Computer Vision I, Lecture 11, LoG Edge and Blob Finding, p19

SIFT erkennt Feature-Punkte, indem mehrere Ebenen vorbereitet werden, die für dieses $ \ sigma $ (Skalierungsraum) angepasst sind. Das Folgende ist die Abbildung.

Um die Berechnung von LoG zu vereinfachen, wird hier die Approximation durch die Differenz zwischen den beiden Schichten mit unterschiedlichem $ \ sigma $ durchgeführt. Dies ist das DoG (Difference of Gaussian). Die gefundenen Merkmalspunkte werden mit der vorherigen und der nächsten Skala verglichen, um festzustellen, ob sie gegenüber der Skala robust sind (verglichen mit 8 Punkten um und 9 Punkten auf der vorderen und hinteren Skala für insgesamt 26 Punkte).

Jetzt können Sie die robusten Funktionen auf der Skala sehen. Der Rest ist die "Stärke" und "Richtung" des Änderungsbetrags an diesem Merkmalspunkt, der sich aus dem Änderungsbetrag und seinem Winkel ergibt.

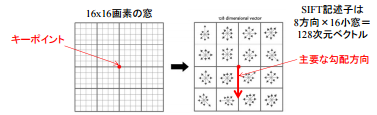
Hier berücksichtigt SIFT nicht nur einen einzelnen Merkmalspunkt, sondern auch darauf zentrierte 16 * 16-Zellen (die Größe dieser "Masse" wird als [Behältergröße] bezeichnet (http: // www). .vlfeat.org / api / sift.html)).

Semantische Multimedia-Verarbeitung A2, S. 4

Teilen Sie es in 4x4-Bereiche und erstellen Sie ein Histogramm mit der vertikalen Achse als Änderungsbetrag (Magitude des Änderungsbetrags) und der horizontalen Achse als Richtung (= Winkel des Gradienten des Änderungsbetrags).

CSE/EE486 Computer Vision I, Lecture 31, Object Recognition : SIFT Keys, p24

Die obige Abbildung ist von 0 bis 36 (entsprechend 360 Grad) zusammengefasst, aber schließlich ist sie in 8 Richtungen zusammengefasst. Dann haben Sie einen Vektor, in dem jedes 4 * 4-Fenster Elemente in 8 Richtungen enthält. Dieser 128-dimensionale Vektor ist der SIFT-Vektor, bei dem es sich um eine Merkmalspunktbeschreibung mit drei Merkmalen handelt: Er ist robust gegenüber "Skalierung", und "Stärke" und "Richtung" können bekannt sein.

Mit diesem SIFT-Vektor können Sie Feature-Punkte mit extrem hoher Genauigkeit abgleichen.

Weiterentwicklung der Merkmalspunkterkennungsmethode

Die oben aufgeführten Methoden zum Erkennen und Beschreiben von Merkmalspunkten entwickeln sich von Jahr zu Jahr weiter. Das Folgende ist die Entwicklung der Methode vor und nach dem Auftreten von SIFT. Sie können den Prozess zum Erhalten von Funktionen sehen, die robust gegen Rotation und Skalierung sind.

MIRU2013 Tutorial: SIFT und nachfolgende Ansätze, S. 5

Dies ist die Entwicklung nach SIFT. Oft wird auch eine Technik namens SURF verwendet, die SIFT beschleunigt. Sowohl SIFT als auch SURF sind patentiert **. SIFT Patent abgelaufen am 6. März 2020 und sogar OpenCV [von NON FREE](https://github.com/ opencv / opencv_contrib / pull / 2449), für die Verwendung von SURF wird jedoch noch eine Patentgebühr erhoben. Daher habe ich bisher erklärt, aber es scheint, dass ORB und AKAZE, die in OpenCV 3.0 hinzugefügt wurden, für den tatsächlichen Gebrauch gut sind. Nichts ist schneller als SIFT / SURF.

MIRU2013 Tutorial: SIFT und nachfolgende Ansätze, S. 93

Wenn Sie die diesmal eingeführten grundlegenden Methoden verstehen, ist es einfacher zu verstehen, was verbessert wurde, wenn in Zukunft neue Methoden erscheinen.

Feature Point Matching

Die erkannten Merkmalspunkte können für verschiedene Zwecke verwendet werden. Als typisches Beispiel möchte ich die Methode zur Bildanpassung vorstellen.

Wenn Bilder abgeglichen werden, besteht der grundlegende Ablauf darin, den Bereich um den zu vergleichenden Merkmalspunkt auszuschneiden (dieser Ausschnitt wird als Patch bezeichnet) und zu prüfen, ob er sich auch im anderen Bild befindet. Werden. Es gibt zwei Arten der Verwendung dieses Patches:

Vorlagenbasiert: Überprüfen Sie das andere Bild auf Übereinstimmung mit dem Patch
Feature-basiert: Extrahieren Sie Features aus einem Patch und prüfen Sie, ob Übereinstimmungen für diese Features vorhanden sind

Das Bild ist in der folgenden Abbildung dargestellt.

In jedem Fall benötigen Sie beim Vergleich eine Funktion, um die Ähnlichkeit zu messen. * Da es schwierig ist, die Ähnlichkeit für den gesamten Bildbereich zu berechnen, muss der Suchbereich eingegrenzt werden, aber ich werde ihn hier nicht berühren.

Das Folgende sind typische Indikatoren zur Messung der Ähnlichkeit.

SSD (Summe der quadratischen Differenzen): Summe der quadratischen Differenzen
NCC (normalisierte Kreuzkorrelation): Normalisierte Kreuzkorrelation

** SSD ** ist der einfachste Index. Wenn Sie sich den Unterschied zwischen Vorlagen und Features ansehen und er nahe bei 0 liegt, wird er als ähnlich angesehen. Für die Entfernung, dh den Schwellenwert, wird häufig das Verhältnis zum am besten passenden Merkmalspunkt verwendet. ** NCC ** oder Interkorrelation ist ein Maß für die Ähnlichkeit und kann durch Berechnung des inneren Produkts erhalten werden. Zum Beispiel sollten Vektoren, die völlig unabhängig sind (= unabhängig voneinander), orthogonal sein, und das innere Produkt der orthogonalen Vektoren wird 0 sein. Im Gegenteil, wenn es nicht 0 ist, gibt es eine positive / negative Korrelation. Dann wird die normalisierte Interkorrelation erhalten, indem normalisiert wird (Mittelwert 0, Varianz 1) und dann die gegenseitige Korrelation genommen wird.

Ich werde auch eine Formel schreiben

SSD(I_1, I_2) = \sum_{[x, y] \in R} (I_1(x, y) - I_2(x, y))^2 \\
C(I_1, I_2) = \sum_{[x, y] \in R} I_1(x, y) I_2(x, y) \\
NCC(I_1, I_2) = \frac{1}{n - 1}\sum_{[x, y] \in R} \frac{(I_1(x, y) - \mu_1)}{\sigma_1} \cdot \frac{(I_2(x, y) - \mu_2)}{\sigma_2}

NCC ist ein Prozess, der aufgrund der Art der Einnahme des inneren Produkts nach Vorlage gefiltert wird. Das Folgende ist ein Beispiel für die tatsächliche Verarbeitung, und Sie können sehen, dass der Teil, der der Vorlage entspricht, reagiert.

CSE/EE486 Computer Vision I, Lecture 7, Template Matching, p7

Wenn Sie einen strengeren Abgleich durchführen möchten, können Sie nicht nur A-> B, sondern auch B-> A abgleichen und nur diejenigen verwenden, die als übereinstimmend beurteilt werden. Mit dieser Feature-Point-Anpassung können Sie Panoramafotos erstellen, Bilder klassifizieren und suchen.

Implementierung in OpenCV

Abschließend werde ich vorstellen, wie es in OpenCV implementiert wird. Ich habe ein Beispiel in Jupyter Notebook im folgenden Repository geschrieben.

icoxfog417/cv_tutorial_feature

Obwohl es sich um eine Installation von OpenCV handelt, wird Anaconda (conda) für Windows empfohlen. Nicht nur Numpy und Matplotlib, sondern auch OpenCV selbst können auf einmal aus der folgenden installiert werden.

menpo/Packages/opencv3

Zur Implementierung habe ich auf das folgende offizielle OpenCV-Tutorial verwiesen.

Der Code, den Sie schreiben, besteht nur aus wenigen Zeilen, wird jedoch ohne Parameteranpassungen (insbesondere SIFT) häufig nicht gut erkannt, und Parameteranpassungen erfordern immer noch ein theoretisches Verständnis. In diesem Sinne denke ich, dass ein theoretisches Verständnis unabdingbar ist, um OpenCV im wahrsten Sinne des Wortes zu beherrschen.

Wir hoffen, dass die diesmal eingeführten Erklärungen Ihnen helfen werden, die Versteinerung zu lösen und ein wahrer Bildverarbeitungsmeister zu werden.

Forschungstrends

Vor kurzem ist das Convolutional Neural Network (CNN) erschienen, und in Bezug auf die Merkmalsextraktion aus Bildern ist das erste, worüber man sich Sorgen machen muss, welches besser ist, die alte Methode oder CNN. Zunächst möchte ich eine Umfrage zu diesem Punkt vorstellen.

CNN hat immer noch ein gewisses Handicap in Bezug auf Lernbedarf und Verarbeitungsgeschwindigkeit, aber es ist immer noch stark darin, dass es verschiedene Aufgaben mit hoher Genauigkeit ausführen kann. Viele der Ideen, die in den von SIFT dargestellten Methoden enthalten sind, sind immer noch nützlich. Daher wird im obigen Artikel vorgeschlagen, dass Sie durch Kombination höher gehen können.

Das Folgende sind Studien zur Merkmalsextraktion unter Verwendung von DNN.

OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks (ICLR, 2014)
Die Methode, die bei der Gebietserkennungsaufgabe von ImageNet 2013 an erster Stelle stand. Anstatt einfach die Feature Map von CNN zu verwenden, werden mehrere Arten von Pooling mit leichtem Versatz (unterschiedliche Versätze) angewendet und die Ergebnisse integriert. Dies macht es robust gegen Fehlausrichtungen. Implementierung ist auf GitHub verfügbar
Discriminative Learning of Deep Convolutional Feature Point Descriptors (ICCV, 2015)
Eine Methode zum Eingeben von zwei Bildfeldern und zum Trainieren mit einem Fehler (ähnlich oder unähnlich) zwischen ihnen.
Sie können die GitHub-Implementierung auf der obigen Seite sehen.
Es gibt auch eine Studie des gleichen Autors mit dem Titel Extrahieren von Merkmalen von Modebildern.
Adversarial Autoencoders (2015)
Die Anwendung von GAN, die sich bei der Erzeugung von Bildern durchgesetzt hat, schreitet ebenfalls voran. Dies verwendet GAN, um die Differenz zwischen der Normalverteilung und der Stichprobe zu berechnen, die der Schwachpunkt von VAE war. Klicken Sie hier für eine Zusammenfassung.
PN-Net: Conjoined Triple Deep Network for Learning Local Image Descriptors (2016)
Eine Lernmethode mit einem Bild und einer Reihe von positiven / negativen Bildern (Triple), basierend auf einer Idee, die Discriminative ~ ähnelt.
Es scheint, dass eine verbesserte Version angekündigt wurde. Dies wird als tfeat (BMVC, 2016) bezeichnet, und die TensorFlow-Implementierung wurde veröffentlicht. Es gibt auch eine Demo der Gebietserkennung in Echtzeit.
LIFT: Learned Invariant Feature Points (ECCV, 2016)
Merkmalspunkterkennung-> (Rotations-) Winkelschätzung-> (winkelunabhängige) Merkmalsmengenbeschreibungserfassung, die die drei grundlegenden Prozesse der Merkmalserkennung darstellt, die durch Kombination von CNN realisiert werden.
Adversarial Feature Learning (NIPS 2016 Workshop)
Vorschlag eines bidirektionalen GAN-Mechanismus (BiGAN), der versucht, die von GAN erfassten Merkmale durch Rückrechnung durch Anwendung von Adversarial zu erfassen. Die Verwendung selbst könnte auch in anderen Bereichen verwendet werden.
Eine ähnliche Studie ist die Adversarially Learned Inference. Wie Sie auf der Kommentarseite sehen können, ist die Idee fast dieselbe.

Verweise

Praktische Computer Vision Die Erklärung ist ehrlich gesagt ziemlich klar, und ich denke, es ist für Anfänger schwierig, dies allein zu verstehen.
Computer Vision I
Computer Vision Kurs an der Pennsylvania State University. Sehr höflich und leicht zu verstehen
Mobile Computer Vision
Stanfords mobiler Computer Vision Kurs. In der Einführung werden wir eine Weile erklären, wie Android entwickelt wird, und von Stitching + Blending zu Computer Vision. Besonders empfehlenswert für diejenigen, die es in mobile integrieren möchten.
OpenCV Official Es ist ziemlich einfach und verfügt über ein OpenCV-basiertes Codebeispiel. Empfohlen.
Materialien der Graduiertenschule für Informationswissenschaft und Ingenieurwesen der Universität für Telekommunikation Die Geschichte der Bildverarbeitung vom 9 .. Reich an Illustrationen und leicht zu verstehen. Hier sind die Grundlagen der grundlegendsten Bilddifferenzierung.
Semantische Multimediaverarbeitung A2 (15. Oktober 2013) Klicken Sie hier, um SIFT zu verstehen. Sehr leicht zu verstehen
MIRU2013 Tutorial: SIFT und nachfolgende Ansätze Obwohl sich die Erklärung auf SIFT konzentriert, ist der systematische und historische Hintergrund der Methode in der zweiten Hälfte organisiert (92-).
VLFeat Documentation
Dokument der Bibliothek zur Merkmalspunktextraktion von Bildern, die in C usw. verwendet werden können. Englisch aber ziemlich leicht zu verstehen.
Can any one help me understand Deeply SIFT ?
Einführung in Eigenvektoren, Hauptkomponentenanalyse, Kovarianz, Entropie
[Bildsuche (spezifische Objekterkennung) - Klassische Methode, Matching, Deep Learning, Kaggle](https://speakerdeck.com/smly/hua-xiang-jian-suo-te-ding-wu-ti-ren-shi -gu-dian-shou-fa-matutingu-shen-ceng-xue-xi-kaggle? slide = 115)
Ein Dokument, das die in diesem Artikel eingeführte klassische Methode mit der neuesten CNN-basierten Methode zur Merkmalsextraktion aus Bildern zusammenfasst.

[PYTHON] Goldnadel für den Fall, dass sie zu einem Stein wird, wenn man sich die Formel der Bildverarbeitung ansieht